借力基本图形 实现思维破冰

季黎明

(江苏省无锡市河埒中学 214063)

G·波利亚说：“掌握数学就意味着善于解题”.在平时的教学中，我们通过实践总结出了诸多的基本图形，初一平面几何中针对复杂的角度问题提炼出的“锯齿型”、“八字型”，初二全等问题中出现的“大手拉小手”、“倍角包半角”模型，初三相似图形中总结出的“A型相似”、“母子相似”等，这些几何模型以基本图形为立足点，为数学问题的解决提供了有规律可循的策略.学生在解题过程中，借力基本图形，不断突破思维的壁垒，从而实现了数学问题的解决.本文以一道中考模拟题为例，从解法探究的角度来窥探基本图形在解决问题中的重要运用.

一、试题呈现

如图1，二次函数y=ax2+2ax-3a图像与x轴交于A、B两点(点A在点B的右边)，与y轴交于点C.

图1

(1)请直接写出A、B两点的坐标：A____，B____.

(2)若以AB为直径的圆恰好经过这个二次函数图像的顶点.

①求这个二次函数的表达式；

②若P为二次函数图像位于第二象限部分上的一点，过点P作PQ平行于y轴，交直线BC于点Q.连接OQ、

二、试题分析

图2 图3

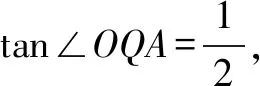
三、解法赏析

1.寻等角，构相似

2.寻圆周角，构造圆

图4 图5

3.作垂直，构相似

四、解题感悟

在对这道题解法的探索中，我们发现解法1借助母子相似来建立等式确定参数m的值确实是最便捷的方案.在解法3中出现了双参数，我们试图建立参数m和n之间的关系以达到消元的目的.在教学当中，我们应当引导学生在求解综合题时，要从不同的角度来思考解决方法，不断地优化解题策略.在追求最优化解题策略的过程中，注重对基本图形与结构的把握.