WELM-Adaboost 算法及在小麦赤霉病流行强度预测中的应用

付强，关海鸥

（黑龙江八一农垦大学电气与信息学院，大庆163319）

在我国，小麦生产比重高、产量大，是国民最主要的粮食作物。小麦的生长过程中，常常会遭受很多自然灾害的侵袭，比如真菌、暴风、寒流等，这些病害、冻害等的产生会严重影响小麦产量甚至造成绝收。而小麦赤霉病就是其中严重影响小麦产量和品质的作物流行病之一。自有统计以来，黑龙江省也曾多次遭受到小麦赤霉病的侵袭，其中，在1959 年全省小麦因赤霉病而减产20%～50%。而在1981 年全省国营农场又因小麦赤霉病即损失粮食近3.5 亿kg[1]。因此，准确地对小麦赤霉病的流行强度做出预测，对黑龙江省小麦的生产活动具有重要意义。

随着互联网技术以及通信技术的不断发展与进步，“人工智能”时代已经来临，越来越多的传统行业依托“机器学习”等现代计算机技术，不断的更新甚至被颠覆，人工智能在农业领域也已经得到了广泛的应用，对农作物病虫害预测等问题提供了一定的参考和借鉴作用。

目前利用人工智能技术对农作物病虫害预测的研究有很多，时雨[2]以安徽省太和县近年小麦赤霉病的发生流行情况作为研究对象，提取病原、寄主和气候等3 方面数据，利用统计分析的方法，总结出了长期气象指标和短期气象指标分别对小麦赤霉病发生情况的影响，提出了基于气候因素的小麦赤霉病预测预报方法；2017 年，吴亚琴[3]通过分析中国中部地区近十年来小麦赤霉病发生情况以及气候数据，分别建立了含有气象因子交叉项的逐步回归模型以及含有气象因子的多元线性逐步回归模型；2019 年，马晓丹[4]根据农作物在发生病虫害时，其冠层图像特征难以提取的问题，将数字图像处理技术与多维特征选取机制相结合，并融入到了大田农作物生长过程中病虫害预测与预报问题中来，为农作物全面系统地开展生长过程监测及病害防治提供重要理论支持；2017 年，张友华等[5]利用神经网络中激活函数所具有的映射能力，采用Fletcher-Reeves 算法的变梯度反向传播算法，建立了小麦赤霉病的气象预报模型，实验表明该算法对小麦赤霉病的预防工作具有一定的参考价值。

以上研究主要集中对大量数据进行统计分析，建立回归方程的方法对小麦赤霉病的流行强度进行预测，但是回归分析法需要对大量样本数据进行分析才能得到较准确的规律，同时容易出现过拟合的状况，当数据量不是很充足的情况下，该方法难以得到准确的预测结果。利用极限学习机算法的小样本寻优和良好的泛化能力，对小麦赤霉病的流行强度预测展开研究，同时，基于小麦赤霉病的流行强度样本分布不均衡的特点，构建了Weighted-ELM 算法与Adaboost 算法融合的模型，验证了该算法对小麦赤霉病流行强度预测的可行性。

1 实验数据集及评价指标

对所采用的数据集以及研究所采用的评价指标即AUC 值分别作简要介绍。

1.1 数据集介绍

根据前人的研究，小麦赤霉病属气候型流行性病害，即其发生的速度和强度均受到气候因素的影响[6]。在农学专家研究的基础上，利用黑龙江省八五四农场所累积的23 年的田间赤霉病情与气象资料作为基础数据，包含平均相对湿度、降雨量、降雨日数、日照时数4 个气候因素，同时，这里将病害分为了两个等级，分别用“强”、“弱”表示小麦赤霉病的流行程度，其中“强”代表病穗率高于20%的情况，对输入数据进行标准化处理并添加流行强度后[7]，样本数据如表1 所示。

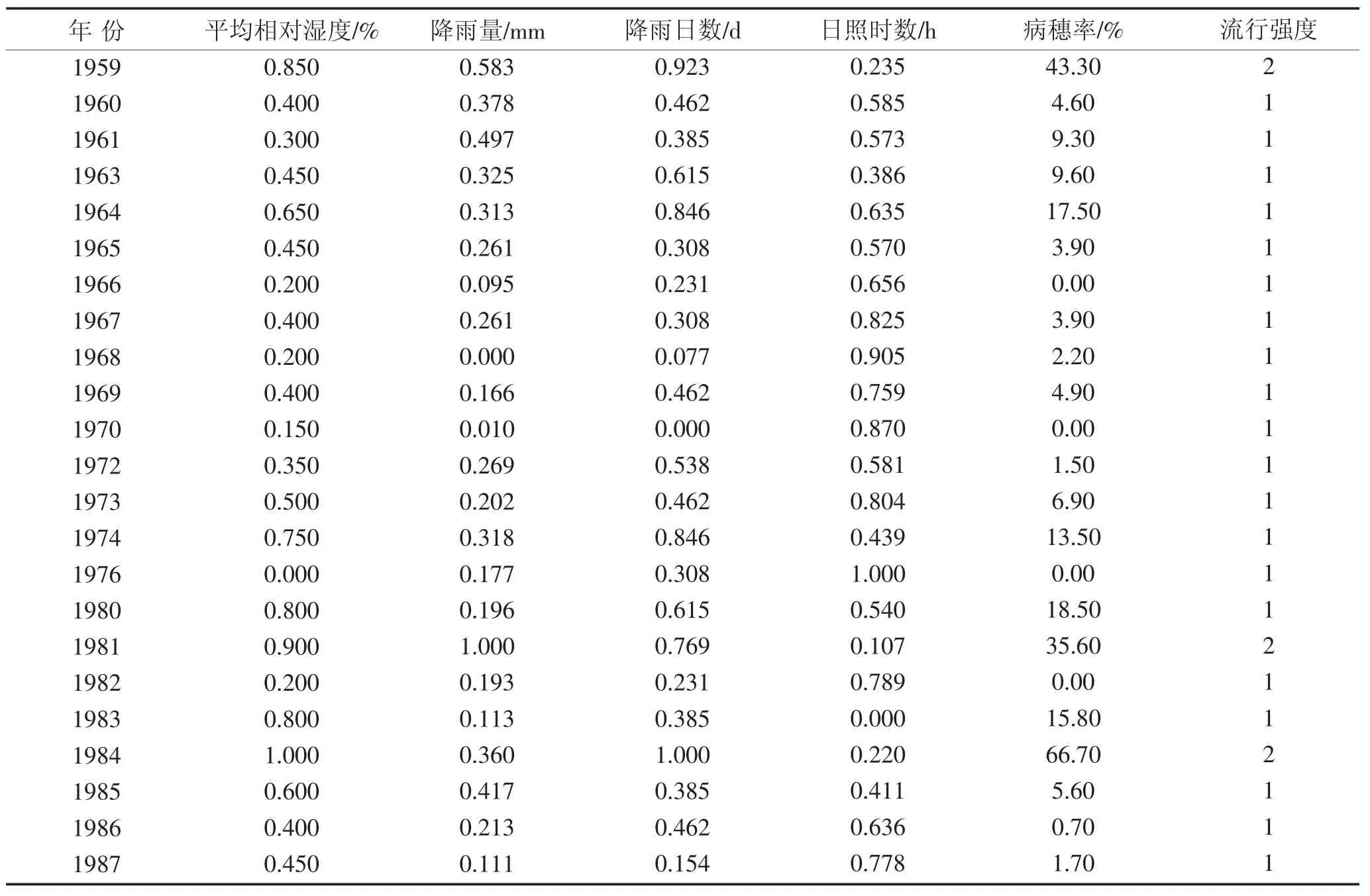
表1 实验数据统计信息Table 1 Experimental data statistics

从表中可以发现，实验数据中，流行程度强与弱的比例约为1∶7，样本的分布并不均衡，这就为模型建立带来了巨大的挑战。

1.2 评价指标

通过上述分析，小麦赤霉病流行强度预测可以看作是一个二分类问题，并且正负样本比例并不均衡，在数据中，小麦赤霉病流行程度的强弱比为1∶7左右，准确度（Accuracy）这样的评价指标不能很好的反应分类器的性能[8]。

为了解决上述问题，人们从医疗分析领域引入ROC 曲线（Receiver Operating Characteristic）作为分类不均衡问题的判别指标，继而应用到数据挖掘、机器学习和模式识别等领域[9]。ROC 曲线是一种二维平面曲线，其横纵坐标分别是FPR（False Positive Rate）和 TPR（True Positive Rate），二者可以根据公式 1、2计算得到。

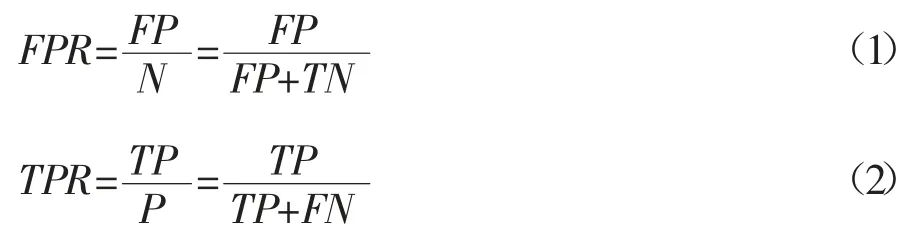
对于二分类问题，TP、FP、TN、FN 分别称为真正例、假正例、真反例以及假反例[10]，四个参数的具体含义如表2 所示。

表2 分类结果的混淆矩阵Table 2 Confusion matrix of classification results

对于某个分类器而言，其分类结果可以映射为ROC 曲线平面上的某个点，不断调整分类器的分类阈值，便可以得到一条经过点（1，1）和点（0，0）的曲线。在小麦赤霉病流行程度预测问题中，将流行程度为强的样本作为正类，流行强度为弱的样本作为负类，对小麦赤霉病流行强度的预测结果进行排序，根据阈值选择的不同，可以生成 ROC 曲线，很明显，算法的预测精度越高，ROC 曲线下的面积越大，即AUC（Area Under Curve）越大。

2 ELM 算法介绍

极限学习机（Extreme Learning Machine）算法是一种新型的神经网络模型，与传统的BP 神经网络相比，该算法的隐层节点内权值和偏置值都是随机选取的，不需要进行迭代来调节网络参数，因此训练速度得到大幅提升，同时还能获得全局最优解，对于数据集的泛化能力很强。随着ELM 算法的不断发展，基于样本分部不均衡的特点，带有权重的极限学习机（Weighted Extreme Learning Machine）模型又被提出。

2.1 ELM 算法

近年来，随着对神经网络学习算法的研究不断深入，Huang G.B 等[11]学者于2004 年提出了一种快速的单隐层神经网络算法即极限学习机（ELM）算法。ELM 算法的具体网络结构如图1 所示[12]。

图1 ELM 神经网络结构Fig.1 ELM neural network structure

传统神经网络模型隐层节点的权值和偏置均是通过误差的反向传播算法不断迭代而确定的，而ELM 算法的值是随机选取的，不需要一系列的迭代算法进行调节[13]。除此之外，ELM 算法中隐藏层到输出层的权值是利用最小二乘法来求解的，不需要任何迭代步骤，所以该神经网络的参数确定过程是非常简单的，缩短了该模型的训练时间[14]。

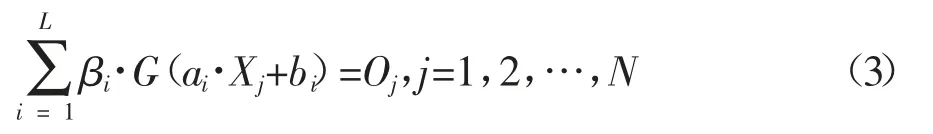
式中，G（aX+b）称作神经网络中隐层节点的激励函数，通常为 sigmoid，sin，hardlim，tribas 等函数，ai为第i 个隐层节点与输入节点的连接权值，bi为第i 个隐层节点的偏置，βi为隐层节点与输出节点之间的连接权值。

在算法的实际应用中，希望网络的输出值与实际的输出值相等或者是很接近，如在上述样本集中，通过神经网络后以零误差接近目标值T，则有‖Hβ-T‖=0，即ELM 算法的公式可以简记为：

式中，H 为神经网络隐层节点输出矩阵；β 为隐层与网络输出层之间的外权矩阵。

该算法求出外权矩阵β 的主要思想是使训练误差‖H β-T‖2和输出外权矩阵的模‖β‖最小，即使下式的值为最小，

也就是寻找最小二乘解β，可以得到：

其中HΓ为H 的广义逆矩阵，当HTH 是非奇异可逆矩阵时，HΓ=（HTH）-1HT；当 HHT是非奇异可逆矩阵时，HΓ=HT（HHT）-1。而当隐层节点输出矩阵H 非列满秩的情况，最优外权β 向量可以利用奇异值分解（SVD）的方法得到[15]。

经过上述一系列的方法得到ELM 算法中的外权矩阵β，隐层节点输出矩阵H 由随机生成的节点参数确定，那么这个神经网络的模型结构就确定下来了，再运用测试样本经过该神经网络，就可以直接得到网络的输出值。

2.2 Weighted-ELM 算法

上节介绍的是基本的ELM 算法，然而现实生活中会遇到诸多分类样本不平衡的情况，比如小麦赤霉病流行强度预测问题，再比如故障诊断等。为了解决分类样本不平衡问题，黄广斌等[16]在2013 年提出Weighted-ELM 算法。

基本ELM 算法的优化目标函数为：

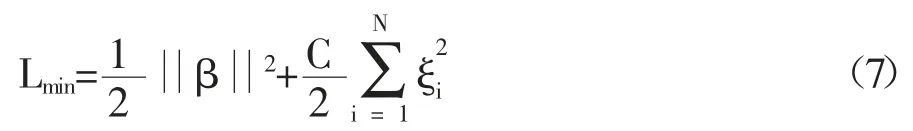
其中，满足的条件是h（Xi）β=ti-ξi，i=1，2，…，N。公式（7）中的前半部分称为结构风险，后半部分称为经验风险。

Weighted-ELM 算法的优化目标函数为：

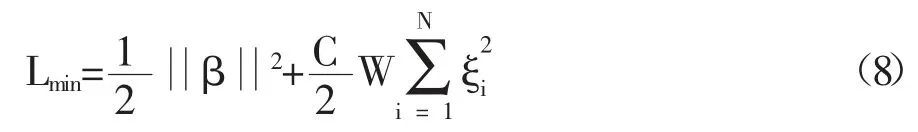
其中，W 是N×N 的对角矩阵，矩阵W 的取值和每个训练样本相关，通常来说，如果Xi属于一个少数并且又是二分类问题中相对重要的类别，那么相应的Wii应该赋予一个相对大的权重。W 的取值方法有两种如下，其中k 是一个可调参数[17]。

第一种W1：

第二种W2：

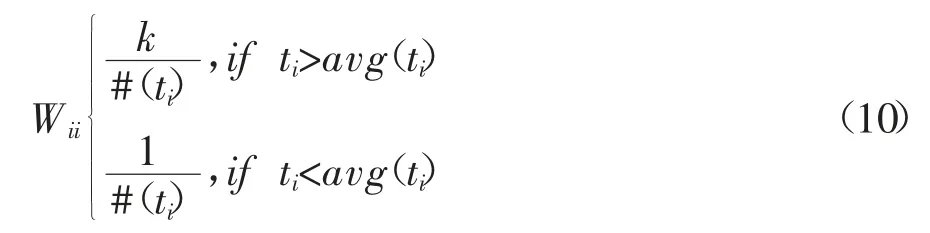
根据KKT 条件，训练ELM 的过程等同于解决下式问题：

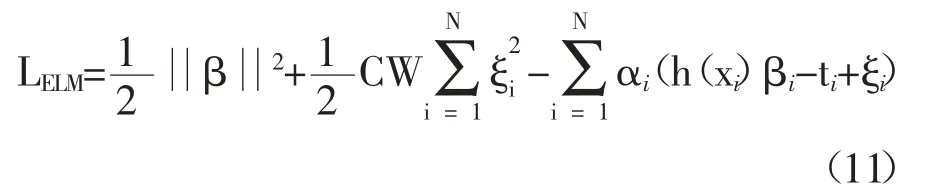
与ELM 相似，β也分两种方式求解：

当，给定一个新的样本X，通过上述确定β 的具体值后，Weighted-ELM 分类器的输出便可简化为：

3 WELM-Adaboost 算法

Weighted-ELM 算法通过调整正负类样本的权重，可以在一定程度上提高预测的精度，但是该算法中，样本的权重是通过各类样本数目的分布而确定的，其大小是固定不变的，对错分样本没有进行进一步的区分，因此，采用可以调整数据分布权值的WELM-Adaboost 算法构建小麦赤霉病流行程度预测模型。

3.1 Adaboost 算法介绍

Boosting 算法是一种集成式的机器学习方法，其思想就是将多个预测能力较弱的分类器通过一定的投票算法而集成为强分类器，Adaboost 算法就是Boosting 思想的典型应用之一[18]。Adaboost 算法选取样本中少量但是比较重要的特征构造多个弱分类器，再将这些弱分类器通过加权的投票机制组合成为强分类器，其优点在于该算法会根据样本的分布以及各个弱分类器的分类效果而调整每个分类器的权重，从而提高算法的预测精度[19]。

3.2 基于WELM-Adaboost 的预测模型

将Weighted-ELM 作为弱预测器，使用Adaboost算法思想不断调整每个样本权重分布，得到多个Weighted-ELM 分类器，将这些分类器组合成一个强分类器[20]。

基于Adaboost 算法和Weighted-ELM 算法的小麦赤霉病流行强度预测流程如图2 所示。

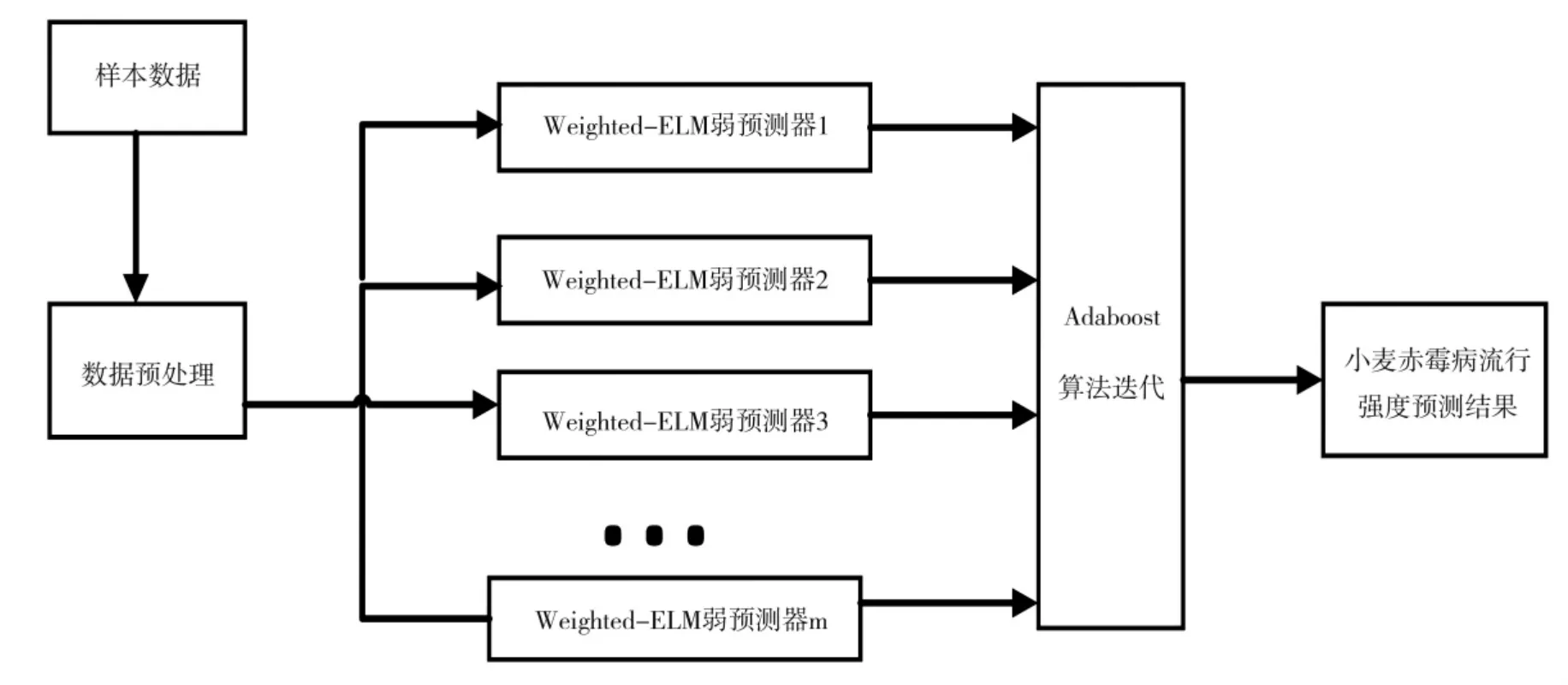
图2 基于WELM-Adaboost 算法小麦赤霉病预测框图Fig.2 Block Diagram of Wheat Scab Prediction Based on WELM-Adaboost Algorithm

算法详细步骤如下：

（1）从样本数据中随机选取N 条作为训练数据，根据其中正负样本的分布比例，初始化不同类别的权值。

（2）对于每次迭代m=1：M，其中M 是所有弱分类器的个数，该算法会重复以下（a）-（e）的步骤：

a）利用训练样本的样本的分布权值，得到第m个弱分类器ELMm；

b）根据由ELMm错分样本的权值计算出权重预测误差和，权重预测误差和的计算公式如（15）所示：

c）依据权重预测和计算出序列权重αm，其公式如（16）所示：

d）根据计算出的序列权重αm调整新的训练样本的权重：

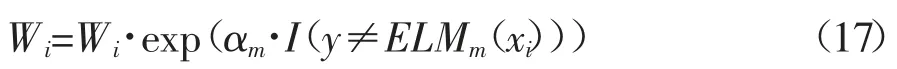
e）重新调整权重分布，在权重比例不变的情况下使分布权值的和为1。

（3）经过M 次迭代后，得到M 组弱预测器，将这些弱预测器融合成最后的强预测器C（x）：

其中k 是样本的类别数。

4 实验设计与结果分析

所采用的实验数据集是黑龙江省八五四农场所累积的23 年的田间赤霉病情与气象资料作为基础数据，样本个数不是很充足，因此，为了衡量算法的准确性，采用交叉验证的方式，每次实验随机选取16个样本作为训练集，其余7 个样本作为预测集，且保证每次实验的训练集和测试集中均包含正样本。那么，根据实验数据的特点，共可以生成六种训练集与测试集的组合。

4.1 模型参数选择

ELM 算法提供了五种激活函数，分别是sigmoid、sin、hardlim、tribas、radbas，经过大量实验表明，不同激活函数对算法预测速度和精度的影响不是很明显。因此，综合考虑训练时间和设备开销，选定ELM 算法、BP 神经网络算法和 WELM-Adaboost 算法的网络的隐层节点个数均为8，激活函数设定为sin 函数。

4.2 算法比较

最后选取了传统的BP 神经网络算法与普通的Weighted-ELM 算法作为对比方法，进行多次实验后，得出三种算法的AUC 结果的对比如表3 所示：

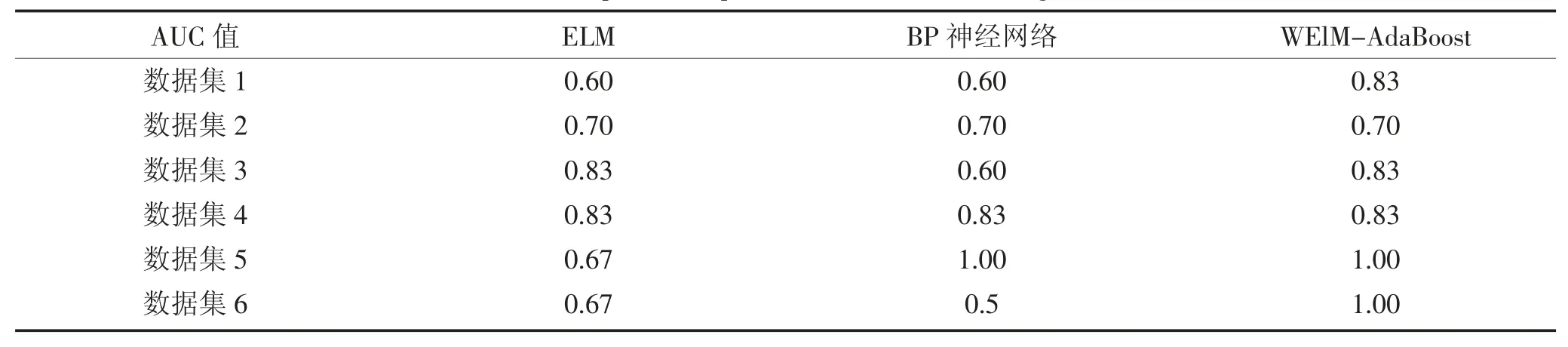
表3 三种算法预测结果比较Table 3 Comparison of prediction results of three algorithms

根据表中数据可得，对于6 组数据集的预测结果，WELM-Adaboost 算法的平均 AUC 值为 0.865，高于 BP 神经网络算法的 0.705 以及 ELM 算法的0.717，WELM-AdaBoost 算法的预测准确性明显优于另外两种算法，这说明所采用的WELM-Adaboost 算法预测小麦赤霉病的流行强度是合理的。

5 总结与展望

对小麦赤霉病流行强度进行准确预测，能够针对性的采取防止措施，对小麦赤霉病的预防具有重大意义。主要贡献有：

提出了基于WELM-Adaboost 算法的小麦赤霉病流行强度预测的方法。以平均相对湿度、降雨量、降雨日数、日照时数4 个气候因素作为预测模型的输入，并与标准的BP 神经网络算法以及ELM 算法作比较，使用AUC 值作为衡量标准，实验结果表明，在不同的数据集下，所采用的WELM-Adaboost 算法的AUC 值明显高于另外两种算法。

尽管对小麦赤霉病的预测取得了一定成果，但是仍有许多问题需要改进与完善。

实验中，数据样本数不够多，尤其缺少流行强度较高的样本，使得WELM-AdaBoost 算法的训练精度不够。同时，所采用的对照算法比较少，至于哪种算法在精度和速度上更占优势有待进一步研究。