基于动力数值分析的抛锚航速
2021-03-10吴卫兵
吴卫兵
(大连海事大学 航海学院, 辽宁 大连 116026)
挪威和德国劳氏船级社(Det Norske Veritas Germcunischer Lloyd, DNV GL)调查数据[1]显示每年千艘船舶丢锚事故数为8~10起,其中油船、化学品船和客船占比较高。由于锚泊操作不当导致的事故占锚泊事故总数的20%以上,抛锚的航速控制不当是锚泊事故发生的主要原因之一。抛锚时船舶的动能应会被船体受到的风阻力、水流阻力以及锚链的拉力做功抵消,如抛锚航速太快则会导致拖锚,或者锚、锚链和锚机等设备的损坏,严重时可能会导致发生搁浅、碰撞和人员伤亡等事故。显然,抛锚航速越小,越利于保护锚设备。但抛锚航速太小将使操纵船舶到抛锚位置的难度加大,并且抛锚时还有可能使锚链在海底堆积,严重时会出现锚与锚链绞缠的现象。因此,抛锚航速是判断锚泊作业安全的一个重要参数。目前,锚泊操纵运动数学模型、船舶抛锚作业和锚泊操纵的方法等相关研究较多,如:王飞[2]建立用于预报分析船舶在锚泊操纵全过程中各种动态运动响应的船舶锚泊操纵运动数学模型,并设计一种锚抓力的数学计算模型;岩井聪[3]利用动能定理构建船舶受力、位移、船舶质量以及航速之间的数学关系模型;顾明章[4]提出大型集装箱船舶进抛法定点锚泊操纵的方法;富志禹等[5]运用牛顿力学定律描述船舶拖锚淌航的过程,并计算船体阻力和附加惯性力;陆冬青等[6]提出锚在海底移动的运动方程,并在考虑锚在海底移动的距离、锚杆仰角、锚型和底质等因素的基础上,计算锚的运动和船体的运动态势,建立了一种基于船舶操纵运动数学模型研究小组(Ship Manoeuvring Mathematical Model Group, MMG)模型建立船舶抛起锚操纵运动数学模型; MCDOWALL[7]在总结航海实践中大型船舶抛锚经验的基础上,运用牛顿力学定律和能量守恒定理建立大型船舶抛锚的运动数学模型,将船舶余速所致的动能分解成艏艉和正横2个方向上外力做功的矢量和,并分别进行计算出大型船舶抛锚航速的推荐值;唐天国[8]在流体动力学原理的基础上,建立舰船锚泊运动的动力学模型和非线性波浪力的数学模型,并对舰船锚泊运动和六自由度操纵运动进行研究。目前,专门针对抛锚航速的定量研究相对较少,在航海实践中主要依靠经验数据作为支撑。因此,有必要对抛锚航速进行定量研究,在参考船舶动能定理模型的基础上,综合考虑锚在触底至抓牢过程中,做功对船舶动能的消耗和锚机设计的刹车力,选取小型、中型、大型和超大型等4种实船船型参数进行计算,并将计算值与经验值进行比较分析,最后建议各种船型的抛锚航速,以便在航海实践中抛锚作业时提供参考。
1 抛锚航速与锚链受力关系数学模型
当锚触底并抓牢不再移动时,抛锚时船舶余速所产生的动能应等于船体受到的外力做功之和。这些外力包括锚链张力、船体受到的水流阻力和风阻力。按照良好船艺的要求,抛锚前将调整船舶航向至顶风顶流方向。根据文献[3]提出的船舶动能定理船舶抛锚前余速所致的动能与外力做功关系为
(1)
式(1)中:Fw为船舶受到的风阻力,N;FV为船体受到的水阻力,N;FA为锚链张力,N;SV为抛锚至停船时船舶前进的水平距离,m;SA为锚触底至抓牢时移动的水平距离,m;MV和ME分别为船舶质量和附加质量,ME=0.1MV,kg;v为船舶抛锚时船舶的对地航速,m/s。
根据《港口工程荷载规范》[9]计算船舶受到的风阻力和水流阻力。
1.1 风阻力
(2)
(3)
式(2)和式(3)中Fxw和Fyw分别为风阻力的横向和纵向分力,kN;Axw和Ayw分别为横向和纵向受风面积,m2;Vxw和Vyw分别为风速的横向和纵向分量,m/s;ζ1和ζ2分别为风压不均匀折减系数和风压高度变化修正系数,其取值见表1和表2。Fw应为Fxw和Fyw的合力,当船舶顶风抛锚时,风阻力Fw=Fyw。
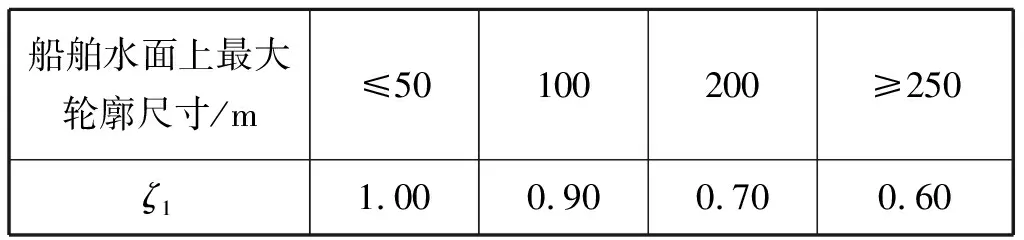
表1 风压不均匀折减系数[9]

表2 风压高度变化修正系数[9]
1.2 水流阻力
抛锚时航速一般较小,兴波阻力和涡流阻力也很小,因此,船体受到的水流阻力主要考虑黏性阻力为
(4)
式(4)中:FV为水流黏性阻力,N;ρ为水密度,kg/m3;AV为船舶吃水线以下的表面积,m2;vTW为船舶对水航速,为实际对地航速与流速的矢量差,当船舶顶流抛锚时,vTW则为抛锚航速v与流速的代数和,m/s;Cv为水流纵向分力系数。
Av的计算为
Av=1.7LD+CbLB
(5)
式(5)中:L为船长,m;D为船舶吃水,m;B为船宽,m;Cb为方形系数。
水阻力系数计算为
CV=0.046Re-0.134+b
(6)
(7)
式(7)中:Re为水流对船舶作用的雷诺数;b为系数;v1为水的运动黏性系数,与水温有关。
2 抛锚工况及参数取值
2.1 抛锚场景设置
选取小型、中型、大型和超大型等4种实船船型参数进行计算。小型船参数采用某3 000吨级的集装箱散货两用船,中型船参数采用某1.8万吨级灵便型散货船,大型船舶参数采用某82 000tDW巴拿马型散货船,超大型船采用某超大型油船(Very Large Grude Carrier, VLCC)船型实船参数。选择计算船型尺度及其相关参数见表3。
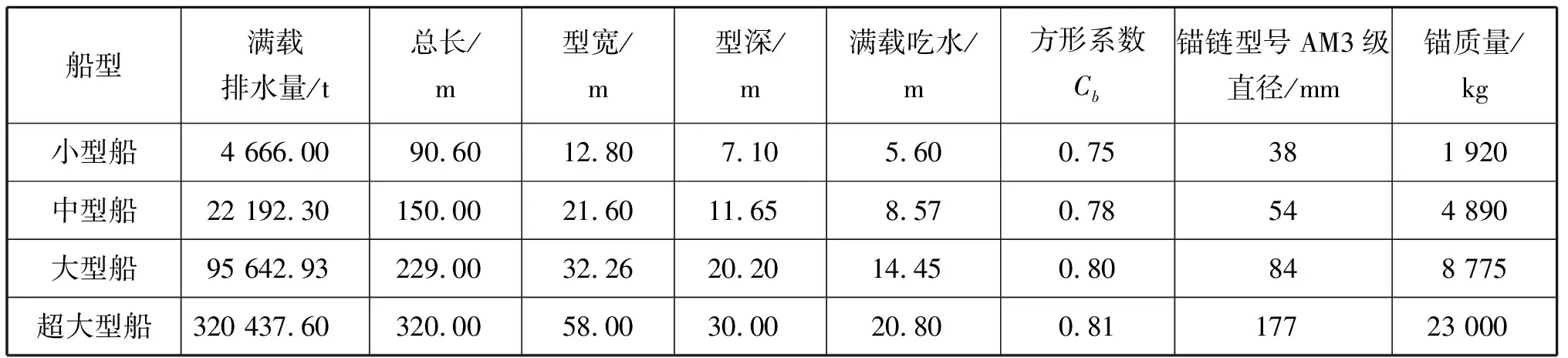
表3 选择船型尺度及其相关参数[10-12]
锚泊水域按照一般港口水域锚地设置,选取锚地水深小型船舶20 m,其他船型30 m,底质良好,锚触底后移动10 m(SA,约5倍锚杆长度)抓牢。[10]
在出链长度为3节(82.5 m)锚链、4节(110.0 m)锚链、5节(137.5 m)锚链和6节(165.0 m)锚链等4种工况下,分别计算在不拖锚和不损坏锚设备时的抛锚航速极限值。
在航海实践中主要有退速抛锚和进速抛锚2种抛锚方式。相较退速抛锚方式进速抛锚具有便于控制锚位和抛锚作业耗时短等优点,因此在航海实践中被广泛采用。在退速抛锚过程中,需倒车至停船后继续倒车船舶才会出现退速,控制到较小的退速抛锚相对较易。船舶因退速太快而导致抛锚事故情况非常少见。因此,选取对控制抛锚航速有较大难度的进速抛锚方式进行数值计算。风阻力做功远小于水阻力做功,因此,计算过程忽略风的影响,船舶顶流抛锚时实际控制的抛锚航速等于不考虑在水流影响情况下的计算抛锚航速值与水流速度值的代数和。综上所述,计算抛锚航速极限值时选择无风流水域。
2.2 SV和SA取值
对应上述4种工况下船舶的水平位移量SV为
(8)
式(8)中:LA为出链长度,m;DW为水深,m。
代入数值计算在4种计算工况下的船舶水平位移量SV值分别见表4和表5。

表4 小型船舶的SV值 m

表5 中型、大型和超大型船舶的SV值 m
2.3 b和v1取值
b和v1的插取值见表6和表7。
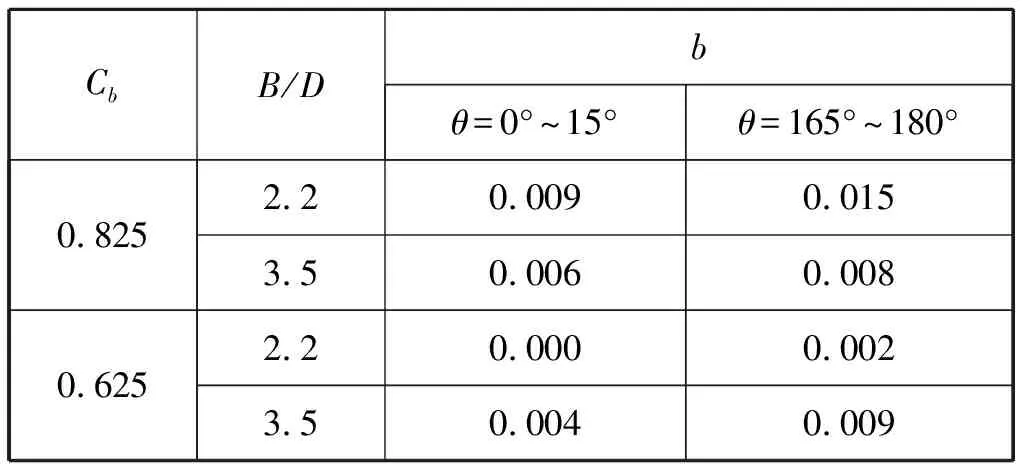
表6 b取值表[9]

表7 v1取值表[9]
表6和表7中:D为船舶吃水,m;B为船宽,m;θ为水流方向与船舶纵轴之间的夹角,(°);油船、散货船和河驳的Cb取0.825;杂货船、河船的Cb取0.625。
综上,在水温15℃时v1取1.14×10-4m2/s;选择计算小型、中型、大型和超大型船舶的b分别为0.002 4、0.013 3、0.014 8和0.011 8。
3 锚机刹车力与锚抓力
中国船级社《钢制海船入级规范》[14]规定:设置有止链器的锚机刹车力不应小于锚链破断负荷的45%,锚链破断负荷按照《电焊锚链》(GBT549—2017)[15]查取。选择计算的小型、中型、大型和超大型船舶的锚链分别为AM3级直径38 mm、54 mm、84 mm和177 mm,锚链的破断负荷分别为1 160 kN、2 270 kN、5 160 kN和9 290 kN;所对应船型的设计锚机的刹车力应该不小于522.0 kN、1 021.5 kN、2 322.0 kN和4 180.5 kN。
锚抓力与底质、锚的类型和锚重等有关。设定泥沙底质,锚抓力与锚链长度和水深的关系表见表8。
链长与水深比为2.75时,选择计算船型的锚抓力为1.8倍水中锚重,则锚抓力分别为45 kN、75 kN、135 kN和353 kN。

表8 锚抓力与锚链长度和水深关系表[12]
显然选择计算船型的设计锚机刹车力明显大于锚抓力,船舶在抛锚时,因航速太快首先将导致拖锚,之后有可能发生损坏锚机刹车的情况。因此,如抛锚时要求相对准确的锚位,不出现拖锚现象,则FA应不大于PA,即FA≤PA;如抛锚有协助减速的目的但要求不应损坏锚机刹车,则FA应不大于PW,即FA≤PW。综上,只需针对FA=PA和FA=PW2种临界状态进行计算,即可获取抛锚航速的2个临界值,分别为不发生拖锚现象和不损坏锚机时的航速最大值。选择计算船型的PA和PW值见表9。
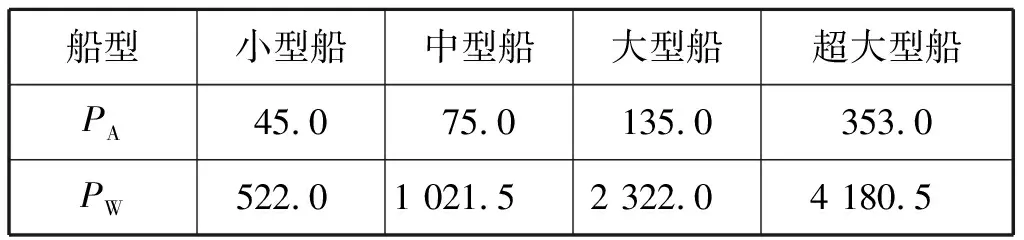
表9 PA和PW值 kN
4 数值计算与分析
4.1 计算结果
分别计算在出链长度为3节、4节、5节和6节锚链等4种工况下锚链张力与抛锚航速的关系,并计算当锚链张力FA分别为PA和PW时的抛锚航速值。计算结果见图1~图4。
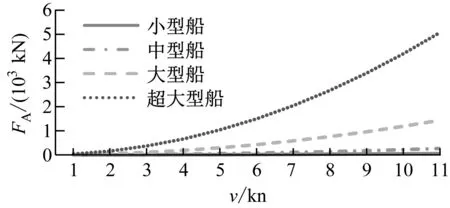
图1 工况1计算结果(3节锚链)
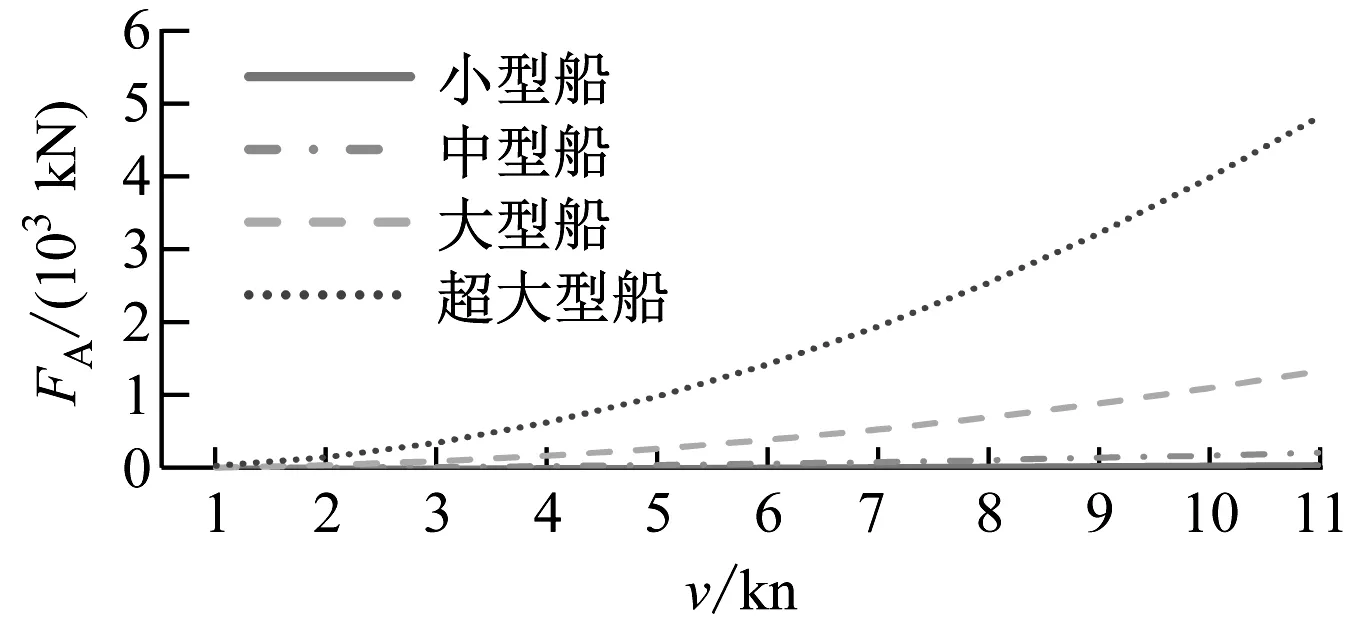
图2 工况2计算结果(4节锚链)
4.2 数值分析
分析计算结果可知:
1)相同的v,船舶排水量越大,FA越大。随着v的增加,排水量越大的船舶,FA增加越明显。
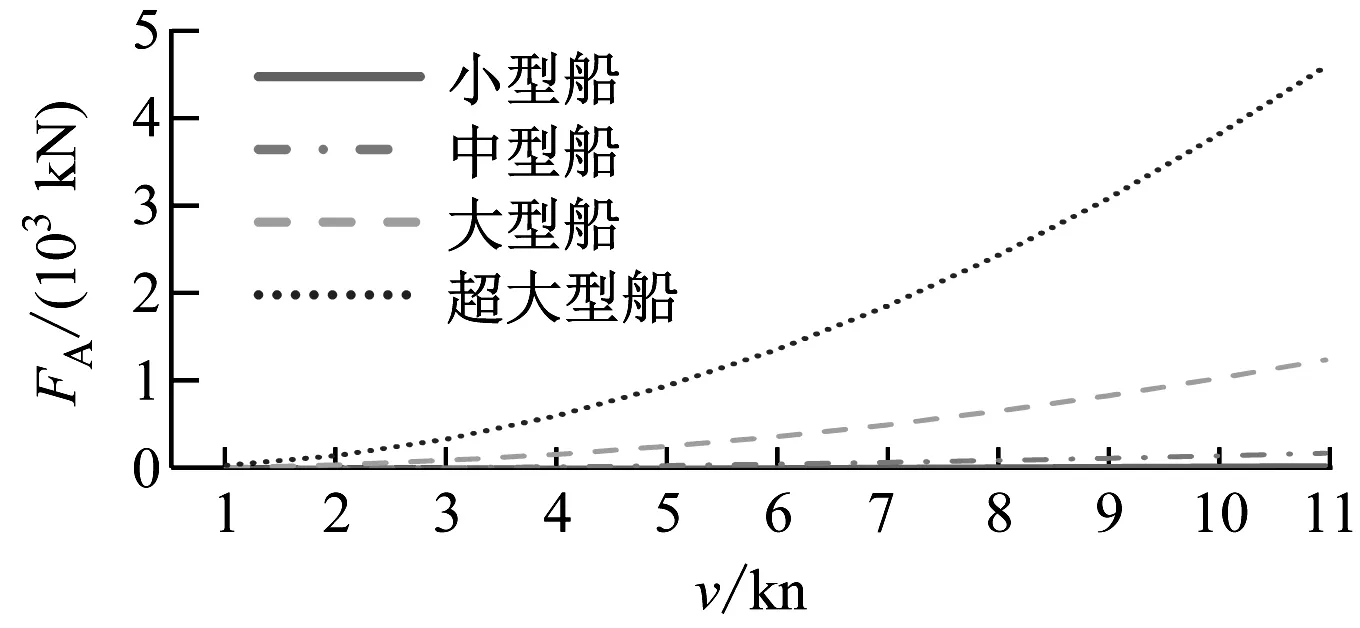
图3 工况3计算结果(5节锚链)
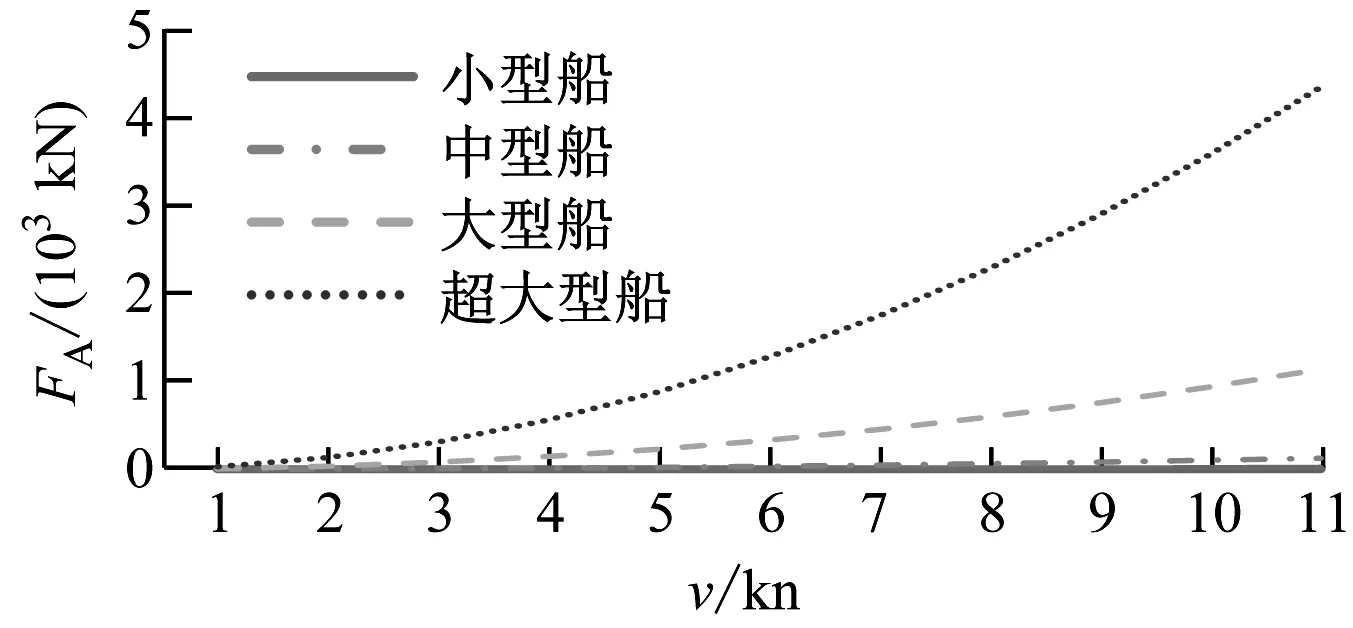
图4 工况4计算结果(6节锚链)
2)抛锚前船舶余速产生的动能主要被船体受到的水流阻力做功抵消,而在锚触底至抓牢过程中锚链张力做功仅为水流阻力做功的0.5%~1.0%。无论是要求不出现拖锚现象(FA≤PA)还是锚机刹车力能控制船舶(FA≤PW),出链长度对同一船型锚链受力和抛锚航速的影响不明显,且随着船舶排水量的增加,影响越不明显。
3)以下分3种情况讨论抛锚航速:
(1)当FA=PA时,计算到的vS为低风险抛锚航速。当抛锚航速以vA不大于vS,即vA≤vS,则FA≤PA,出链后即使完全刹住锚机刹车也不会导致拖锚。因此,该抛锚航速适用于对锚位精度要求较高的抛锚作业,但因抛锚航速值较小,抛锚作业耗时较长,增加抛锚前操纵船舶至指定抛锚位置的难度。
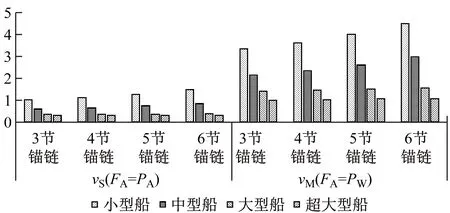
(2)当FA=PW时,计算到的抛锚航速值(vM)为风险可控的抛锚航速,同时也是可抛锚航速的最大值。当vS (3)当vA>vM时,则FA>PW,此时锚链受到的张力大于锚机设计的刹车力并远大于锚抓力,如刹住锚机刹车会导致船舶转向或拖锚来额外做功抵消船舶的动能,如锚在海底拖动过程中卡住将非常危险,很容易造成锚机刹车损坏、丢锚或断链等事故,严重时会导致人员伤亡。vS和vM计算值见表10,其抛锚航速计算结果比较见图5。 表10 vS和vM计算值 kn 图5 FA=PA和FA=PW时的抛锚航速计算结果比较 4)因不同抛锚工况对抛锚航速值影响甚小,故采用在4种工况下计算航速的算术平均值作为抛锚航速的控制值,见表11。小型、中型、大型和超大型等4种计算船型对应的低风险抛锚航速值vS分别为1.2 kn、0.7 kn、0.3 kn和0.3 kn;风险可控抛锚航速值vM分别为3.8 kn、2.5 kn、1.4 kn和1.0 kn。 表11 抛锚航速控制值 kn 1)在计算抛锚航速时,忽略了在锚入水到触底过程中锚受到的水阻力以及锚链与锚链孔之间的摩擦力。因此,抛锚航速的计算值偏小,偏向于安全。 2)抛锚航速计算值是基于在静水中不考虑风载荷做功情况下船舶动能定理,因此对地航速和对水航速相等。实际上,锚泊水域的风和流对抛锚航速的计算值会有一定程度的影响,但从良好船艺角度出发,抛锚前艏部一般迎风顶流,因此,进速抛锚时风和流对船舶做功可额外抵消一部分船舶动能,更有利于船舶减速,锚链实际受到的张力要小于计算值,因此,抛锚航速计算值偏小,有利于抛锚作业安全。实际控制的抛锚航速约为计算值与流速的和。 3)抛锚航速的计算模型在退速抛锚时确定抛锚航速同样适用,但相同航速的进速抛锚和退速抛锚时船舶所受到的水流阻力不一致。抛锚前艏向迎风顶流,船舶后退时风和流对船舶做功在一定程度上增加船舶动能,不利于船舶减速,锚链实际受到的张力大于计算值,因此,计算到的抛锚航速值偏大,不利于抛锚作业安全。 实际控制的抛锚航速应为计算值减去流速。 4)在抛锚实践中,在参考抛锚航速计算值的基础上,船长还应充分考虑到锚泊水域的风、流和浪等自然环境的影响,仔细观察锚链受力情况能尽早发现拖锚,并适时用车控制船舶航速,以保障安全。 文献[13]建议万吨级商船抛锚航速控制在2.0 kn以下,满载1.5 kn以下,超大型船舶0.5 kn以下;文献[16]提出小型船舶控制在2 kn以内,VLCC控制在0.4 kn以内;文献[7]和文献[17]建议万吨级船舶控制在2 kn以内,VLCC一般控制在0.25~0.50 kn。这些经验数据对出链长度和抛锚过程中是否允许出现拖锚现象都未做出界定。对锚位精度要求较高的定点抛锚作业而言,要求不出现拖锚现象时,选择计算的小型船、中型船、大型船和超大型船满载抛锚航速计算值分别为1.2 kn、0.7 kn、0.3 kn和0.3 kn以内;如允许拖锚减速但不至于损坏锚机刹车,则抛锚航速计算值分别为3.8 kn、2.5 kn、1.4 kn和1.0 kn以内。对于中小型船舶在不出现拖锚现象时的抛锚航速计算值小于经验值,超大型船舶计算值与经验值基本吻合。 在留有安全余量的基础上,建议选择计算的小型、中型、大型和超大型船舶满载抛锚航速分别控制为: 1)对锚位精度要求比较高的抛锚作业,要求不出现拖锚现象,则抛锚航速需控制在 1.0 kn、0.5 kn、0.3 kn和0.3 kn以内。 2)对拖锚协助减速的抛锚作业,要求拖锚过程中不至于损坏锚机刹车,则抛锚航速控制在3.0 kn、2.0 kn、1.4 kn和1.0 kn以内。 3)为确保锚和锚设备的安全,建议大型和超大型船舶不采用拖锚减速的方式进行抛锚作业。 4)中小型船舶如采用拖锚减速的方式进行锚泊作业除控制好抛锚航速之外,还应控制好拖锚链长,一般不应超过1.5倍水深,否则锚链与海底的摩擦力将对锚链张力的变化产生不可忽略的影响。 本文建立抛锚航速与锚链受力关系的数学模型,对小型集散两用船、中型散货船、大型散货船和VLCC等4种实船船型满载情况下进行计算,对计算值进行分析,并与经验值进行比较,提出抛锚航速的相关建议。建立的数学模型和计算值可为航海实践中同类型船舶锚泊作业控制航速提供有价值的参考。该模型可应用于其他船型,能在一定程度上提高船舶抛锚作业的安全性,后期还应对更多不同类型船舶的抛锚航速进行深入的研究,并结合实测数据对建立的模型进行适当修正。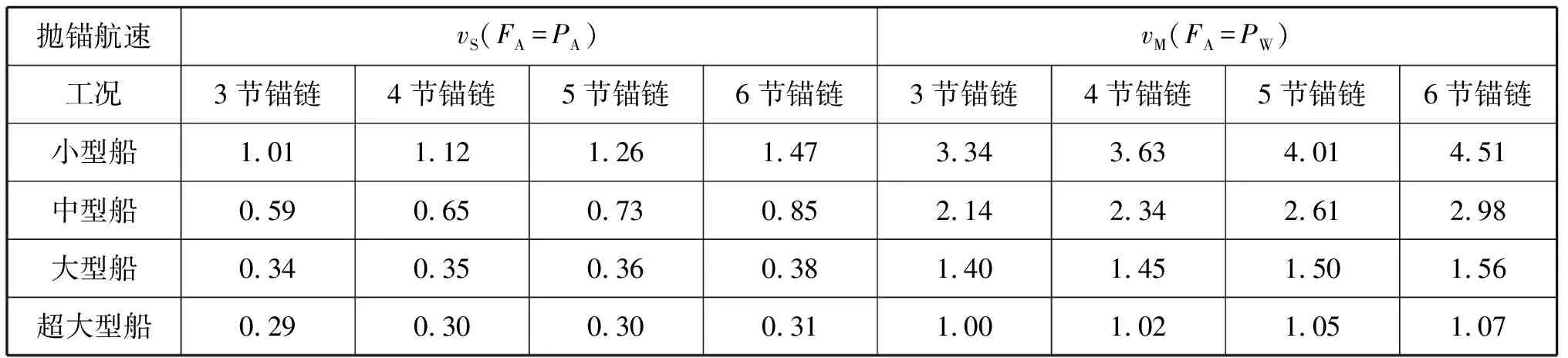

5 计算值局限性分析
6 计算值与经验值比较分析
7 结束语
