框架锚索加固边坡地震响应的动力计算方法浅析
2021-03-09刘蕾蕾牛家永
王 东,刘蕾蕾,余 强,邱 毅,牛家永
(1.四川省公路规划勘察设计研究院有限公司,成都 610041; 2.西南交通大学 土木工程学院,成都 610031)
在岩土工程领域,预应力锚索通过调动深部岩土体的自身强度来改善浅表层岩土体应力状态、提高岩土体整体性、增加软弱面抗滑能力,从而起到加固边坡、治理滑坡和减小地表沉降的作用[1]。在地震动激励下,锚固系统往往产生较大的动附加应力,可使锚固系统失效,引发次生灾害等,因此如何考虑地震工况下锚索的抗震设计已成为岩土工程师亟待解决的问题[2]。
由大量框架锚索加固边坡的振动台模型试验[3-5]可知,地震时边坡沿竖直方向存在加速度放大效应,锚索轴力在地震过程中及地震结束时也将发生改变,地震结束时边坡体可能产生向临空面的变形等,在边坡抗震设计时应重视这些因素[6-8]。
本文以传统锚索设计方法为基础,结合弹性动力学理论、极限分析上限法和地震时边坡的滑移量建立框架锚索的自由段轴力地震响应理论解,可分别求解轴力弹性响应值和锚索轴力残余值。
1 地震作用下锚索轴力响应值
锚索轴力的地震响应值包括弹性响应值和残余变形值,锚固边坡在无残余变形产生时轴力在地震前后的变化量是一致的,可采用结构动力学方程来求解地震作用过程中锚索产生的动应力和锚索的轴力时程曲线。当有残余变形产生时,锚索轴力在地震结束时刻会产生残余值,且轴力大于地震开始时刻,需根据刚性块体滑移理论计算轴力的残余值,再叠加轴力弹性响应值,得到锚索轴力的地震响应值。
1.1 轴力弹性响应值
在地震作用下,框架锚索结构与边坡体的变形处于同步动态变化状态,如图1所示。因此,锚索轴力的时程曲线可通过联合框架梁的位移变化量和锚索材料的力-位移关系间接求出[9]。以框架梁的各节点为质量集中中心,每个质量块的长度为框架梁的纵向间距,将框架梁分为n个质量块,编号为1、2、…、n,此时框架梁可以视为一个具有n个集中质量的多自由度体系,其位移响应值可通过结构动力学理论求出。
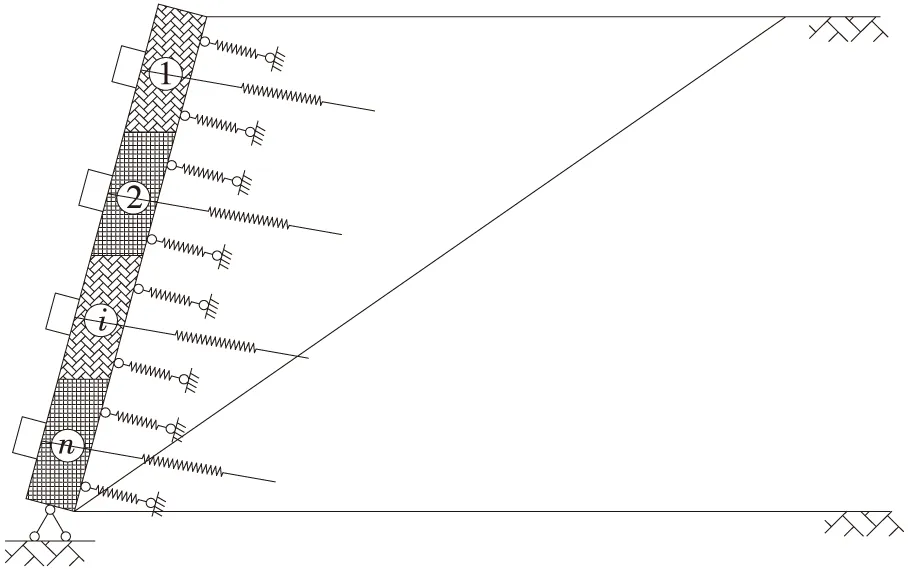
图1 框架梁与边坡体相互作用的简化示意
取框架梁结构中的第j块,如图2所示,建立其地震运动方程。假设框架梁第j层相对于坡脚地面的位移可表达为:
uj(t)=ψjzj(t)j=1,2,…,n
(1)
式中:ψj为定义偏转形状的位移形函数;uj(t)为第j层相对位移;zj(t)为广义位移。
则第j层梁体的绝对位移为:
(2)
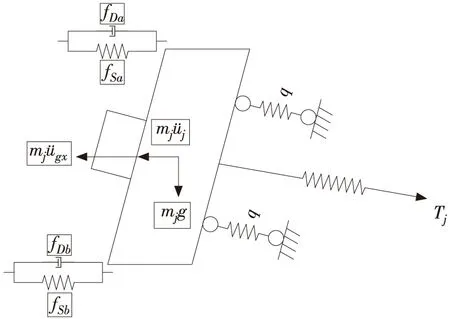
图2 第j块框架梁的动力计算模型
第j层梁体与j+1层间的剪力fSbj,通过层间刚度kj与层间相对位移Δuj=uj-uj+1计算如下:
fSbj=kjΔuj=kj(uj-uj+1)
(3)
其中,层间刚度为:
(4)
式中:EI为框架梁柱的弯曲刚度,kN·m2;lj为第j层梁体的长度,m。
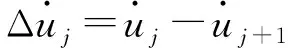
(5)
由于处于弹性变形状态,框架梁的第j层梁体所受外力为地震惯性力、层间剪力和阻尼力、锚索轴力和坡体反力,在地震作用的某一时刻处于平衡状态。框架梁体的运动方程可根据虚位移原理建立,外力在质量为mj的第j层框架梁产生δuj的虚位移时,所做的虚功W可表示为:
(6)
层间位移与框架梁第j层虚位移δuj相关,其层间剪力和阻尼力所做的内力虚功为:
(7)
因外力虚功和内力虚功相等,消去δz后可得:
(8)
令
(9)
则式(8)可化为标准型式的运动方程:
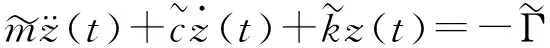
(10)
框架梁纵梁和横梁的截面尺寸分别为a×b和c×b,框架结构的密度为ρk,纵梁从上到下被分成了n段,则
(11)
式中:j=2,3,…,n-1,其中
(12)
式中:H为边坡高度,m;sh、sv分别为锚索框架梁的水平间距和竖直间距,m;hi为第i块土体锚头距坡脚的竖直距离,m。
框架梁第j层的位移值可通过求解上述方程得到,将位移响应值带入式(13)可求得锚索轴力的弹性响应值。
(13)
式中:ΔTj(t)为锚索轴力的地震响应增量,N;lfj为第j孔锚索自由段长度,m;Ej为第j孔锚索的弹性模量,MPa;Aj为第j孔锚索的横截面积,m2;α为锚索的锚固倾角,(°)。
综上所述,地震作用下锚索轴力的弹性响应值可通过以下3个步骤求得:
1) 将框架结构和边坡结构的材料参数和形状参数代入式(11)、(12)中,求出框架体系的集中质量分布状态。
2) 根据给定的框架梁形函数、框架梁各层的剪切刚度和粘滞阻尼系数,由式(8)、(10)求出地震作用下的动力方程,从而得到框架梁各节点位置处的动位移时程曲线。
3) 将位移响应值代入式(13)中,计算得到锚索轴力的弹性响应值,得到时程曲线。
1.2 轴力残余值
假定框架锚索加固边坡的潜在滑动体为刚性块体,滑动模式如图3所示。图3中,ob段为预应力施加后的第j孔锚索自由端长度,记为lfj;bb′段为刚性块体在地震作用下产生的滑移量,记为x;∠bob′为锚索倾角变化值,记为Δα;刚性块体滑移导致第j孔锚索自由段长度变为lfj′,可得锚索自由段的长度变化量为:
(14)
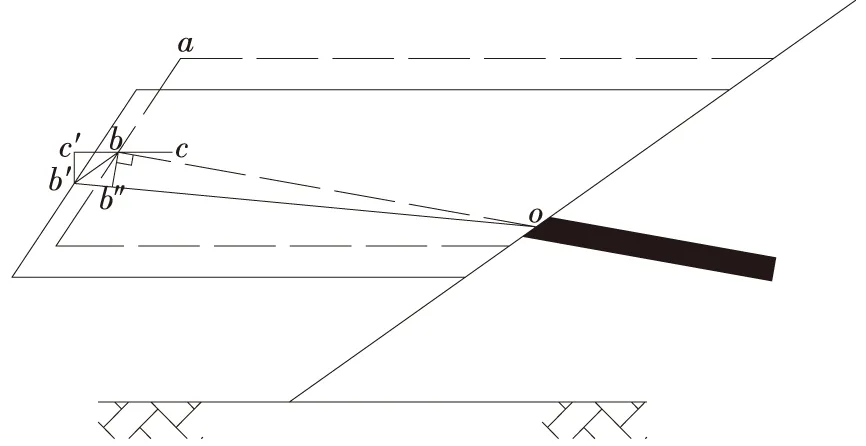
图3 潜在滑体滑移示意
因锚索自由段长度变化引起的轴力增量ΔTi为:
(15)
式中:E为锚固体自由段的弹性模量,MPa;A为锚固体自由段的横截面积,m2;Ti为锚索的初始预应力,N;θ为滑裂面与水平面的夹角,(°)。
锚索轴力残余值时程曲线可按如下3个步骤求得:1) 采用极限分析上限法获得框架锚索加固边坡的临界屈服加速度kc,本文采用文献[10]中的临界屈服加速度进行分析;2) 对于输入的地震动时程曲线,将超过kc的部分进行二次积分,求得锚固边坡的永久位移值,即为残余变形值;3) 根据式(15)求边坡不同高度处锚索残余轴力时程曲线。
2 振动台试验结果对比
为验证本文提出方法的合理性和正确性,将其计算结果与框架锚索振动台模型试验测试结果进行比较。振动台模型试验现场照片如图4所示。模型高1.2 m,由滑体、软弱面和基岩组成,滑体的粘聚力和内摩擦角分别为1.2 kPa和25°,重量为11.4 kN,滑动面与水平面的倾角为33°,采用框架锚索结构加固,从上至下共4排锚索,设计锚固力为0.6 kN,锚固倾角为10°,振动台模型试验详细描述见文献[11]。

图4 振动台试验模型
在振动台模型试验中,首先将地震加速度时程数据输入到控制系统中,通过控制台下方的作动器实现台面的往复运动,从而施加地震力。以0.564g的人工波为计算工况,取坡脚自由场处的加速度时程曲线为输入地震荷载曲线,如图5(a)所示,对超过临界加速度0.5g的部分进行二次积分,得到边坡滑动体的残余位移时程曲线,如图5(b)所示,残余位移时程曲线即为锚索自由端处刚性块体在地震作用下产生的滑移量x,将滑移量x和相关参数带入式(15)中可求得坡底处锚索(文献[11]中标注为J1)的轴力残余值随时间的变化量,如图5(c)所示。试验中轴力残余值可根据地震结束时刻锚索时程曲线相对于初始值的偏移量确定。由图5(c)可知计算得到的残余轴力值为3 N,与试验中J1锚索测得的2.5 N较为接近。由于未考虑边坡发生残余变形时边坡整体临界加速度的改变,所以计算得到的响应值偏大。
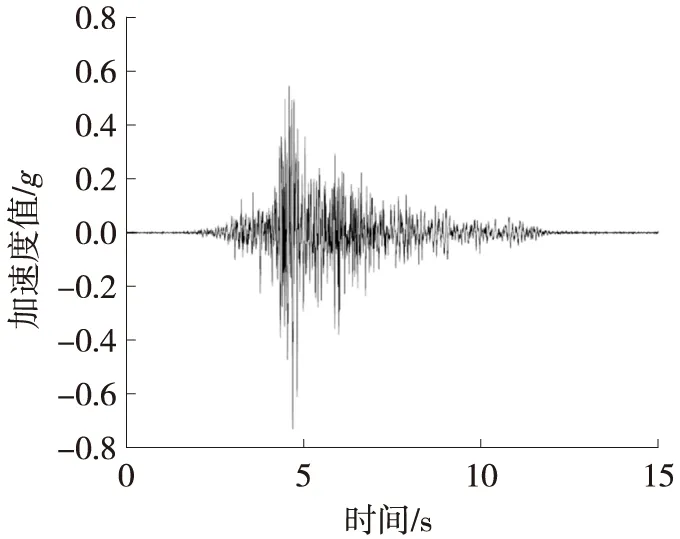
(a) 输入地震荷载曲线
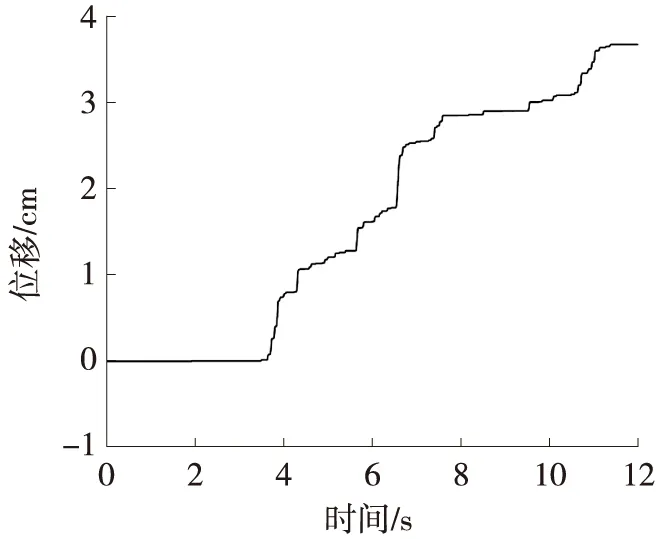
(b) 坡体残余变形曲线

(c) 锚索残余轴力时程曲线
在框架锚索加固边坡的轴力弹性响应值计算中,给定ki=120 kN/m、mi=2.4 kg,并假设框架梁的形函数ψ沿高程呈线性分布,通过公式(8)、(9)可得:
将以上值带入式(10)得:

(16)
已知地震记录的采样时间间隔Δt=0.002 s,采用动力反应的数值计算方法求解公式(16)弹性阶段的广义位移时程曲线,进而获得坡脚处锚索的轴力弹性响应值,以上过程通过Matlab编程实现。将锚索轴力弹性响应时程曲线与轴力残余值时程曲线叠加便可得到锚索轴力实际的地震响应时程曲线。振动台模型试验测得的锚索轴力时程曲线与计算得到的时程曲线的对比如图6所示。由图6可以看出,两者的时程曲线吻合度较好,轴力残余值和轴力响应峰值均较为接近,计算值略大于实测值,但差异不大,据此证明该计算方法是合理的和正确的,当缺少试验数据或数据出现偏差时,用本文提出的计算方法可较准确计算锚索在地震作用下的动态响应时程曲线。
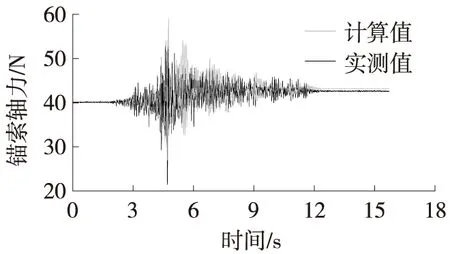
图6 锚索轴力计算结果与振动台试验实测值对比
3 结论
1) 基于多自由度体系的集中质量法,求解框架体系的集中质量分布状态;结合框架梁形状参数、剪切刚度和粘滞阻尼系数,得到各节点的动位移时程曲线,进而得到锚索轴力弹性时程曲线。
2) 通过采用极限分析上限法求解锚固边坡体的临界屈服加速度,对超过临界屈服加速度部分进行积分,求出边坡体的残余变形时程曲线,进而求得锚索轴力随时间的变化值,即锚索轴力残余值的时程曲线。
3) 将计算值与振动台模型试验结果进行了对比分析,验证了文中建立的地震作用下框架锚索轴力响应值计算方法的有效性和准确性。
