DWB-AES：基于AES 的动态白盒实现方法

王滨，陈思，陈加栋，王星

（1.浙江大学电气工程学院，浙江 杭州 310058；2.中国电科集团52 所海康威视网络与信息安全实验室，浙江 杭州 310053）

1 引言

由于物联网感知层的设备受到软硬件资源的各种限制，而传统的密码技术需要消耗较多的资源，从而导致传统的密码技术手段很难直接应用到感知层设备。白盒密码作为一种软密码模块，与传统的密码技术不同，能够隐藏密钥信息、极大地提高物联网设备的安全性，同时能够大幅降低成本，非常适用于对成本敏感的感知层设备。

白盒密码颠覆了传统密码学对攻击者能力的诸多限制，且应用的成本较低，所以更适合应对实际中的安全威胁。目前，白盒密码已经在数字版权保护管理、云上数据软件加解密、移动智能终端信息加密保护等方面得到了较广泛的应用，引起了学术界和产业界的广泛关注。

白盒密码学的概念由Chow 等[1]提出，同时Chow 等[2]通过查找表的方式实现了数据加密标准（DES,data encryption standard）和AES[1]的白盒密码算法。然而，文献[3-4]中提出了对Chow 等白盒DES 算法的有效攻击方法。Billet 等[5]给出了对Chow 等白盒算法的攻击方法，被称为BGE 攻击。在BGE 攻击被提出之后，Xiao 等[6]利用更大的线性编码设计了能抵御BGE 攻击的AES 白盒密码算法。然而Mulder 等[7]以230的时间复杂度提取了Xiao-Lai 白盒算法[6]的密钥。为了抵御Mulder 等的攻击，文献[8]在Xiao-Lai 白盒算法的基础上，通过增加非线性编码的方式设计了新的AES 白盒算法。此外，Karroumi[9]通过引入二元密文的方式实现了AES 白盒密码算法，但是随后由Mulder[10]攻破。Biryukov 等[11]提出了基于ASASA（affine-substitution-affine-substitution-affine）结构的多变量密码体系，并设计了基于ASASA 结构的白盒密码方案，通过插入扰乱项来抵抗攻击。文献[12]以分组密码算法为底层模块，设计了基于底层分组密码算法安全性[13]的白盒密码。文献[14]设计了类AES 的白盒算法。文献[15]设计了一种基于SM4 的白盒算法。此外，近年来还有其他密码算法的白盒实现被研究和设计[16-18]。但是相比于其他白盒实现思路，基于查找表的白盒方案计算相对简单、占用空间较小、计算效率更高。

由于白盒密码是软件实现的，因此可以很好地满足对成本和安全都有较高要求的场景，但是当前白盒密码技术存在以下的问题。

1)灵活性较差。为了保证加解密的安全性，需要定期更换密钥，而现有的白盒算法的表是与密钥绑定的，即静态白盒算法，每次更换密钥需要重新生成和更换表，甚至更换白盒算法库。

2)实用性不好。如前所述，已有的白盒算法要么存在安全设计缺陷，容易被敌手攻击；要么为了提高安全性，增加计算复杂度，需要占用较大的存储和计算资源，这对当前白盒密码的应用场景来说不适用。

基于当前的研究现状和需求，本文提出一种基于查找表的动态AES 白盒算法——DWB-AES，该算法具有以下特点。

1)具有较高的灵活性。每次更换密钥时，不必更新表和白盒算法库，只需要更新很小的白盒密钥信息即可。

2)具有较高的实用性。DWB-AES 加解密过程基于查找表实现，具有较高的运算效率和较低的存储空间需求，尤其适合计算和存储资源受限的物联网设备。

3)具有较高的安全性。DWB-AES 对密钥和表同时混淆，引入16 B 的混淆变换，使其能够抵御现有针对白盒密码的BGE 和Mulder 等常用攻击方法，并且拥有较高的白盒多样性和白盒含混度。

2 AES 静态白盒算法

在白盒攻击环境下，攻击者可以观察到密码算法执行的整个过程，为了保护密钥，可以将加解密过程以表的形式实现，这种思路是由Chow 等提出的。通过查找表，由输入数据直接获取输出数据，从而隐藏了密钥信息。下面，将分别介绍Chow 等白盒实现和Xiao-Lai 白盒算法。

2.1 Chow 等白盒实现

在Chow 等白盒实现里[1]，通过改变轮与轮之间的边界，将加密钥和S盒变换组合在一起，对应一个8 bit 双射，称为T盒变换。以AES-128 为例，第r轮、第i行、第j列的T盒为

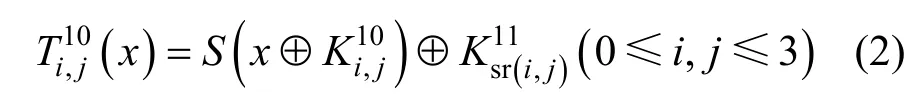
其中，sr(i,j)表示行变换之后的下标。

列混淆操作每次作用在状态矩阵的一列，对应32×32的列混淆矩阵和32×1的列向量相乘。为了减小表大小，将列混淆矩阵MC 分割成4 个部分，即MC=(M C0,MC1,MC2,MC3)，将列混淆操作MC 转换为4 次32×8矩阵和8×1列向量相乘，并对4 个列向量相加。

为了隐藏密钥，需要引入混淆编码。为此，在T盒变换之前引入双射变换，在列混淆操作之后乘32×32矩阵MB，并使用和分割矩阵MC 一样的方法分割矩阵MB。

将T盒变换和列混淆操作结合，生成TypeII 表；TypeII=MB ◦ MC◦T◦ mb，其中，mb 表示引入的双射变换，MB 表示引入的线性变换：乘矩阵MB。为了抵消引入的线性变换和mb 双射变换，引入TypeIII 表，对应实现mb 的逆变换和MB 的逆变换。

此外，为了实现矩阵分割过程中的异或操作，构造异或辅助表TypeIV，实现了4 bit 和4 bit 的异或操作。

2.2 Xiao-Lai 白盒实现

和Chow 等白盒算法类似，Xiao-Lai 的AES白盒实现算法将加密钥操作和S盒变换结合在一起生成T盒，这里不再赘述。与Chow 等白盒算法不同，Xiao-Lai 的AES 白盒实现算法的列混淆操作将 MC 分割成 2 个部分，即MC=(M C0,MC1)，列混淆操作变为2 次32×16矩阵和16×1列向量相乘再相加。

构造表TMC 为

其中，T2i+1和T2i表示相邻的2 个T盒变换，R表示32×32矩阵线性变换，L表示16×16矩阵线性变换。将查表得到的2 个列向量直接相加，得到列混淆的结果。

行变换操作可看作乘128×128矩阵的操作，通过乘随机矩阵来实现混淆，最终得到矩阵M=LSRR−1，其中，L为16×16的矩阵，SR 为行变换矩阵，R为32×32的矩阵，M矩阵既实现了行变换操作，又抵消了TMC 表中引入的线性变换。为了处理外部编码，第一轮的M矩阵引入了输入变换，最后一轮的M矩阵引入了输出变换。

3 AES 动态白盒算法DWB-AES 实现方案

所谓动态白盒算法，就是在密钥更换时，不需要更换查找表，可以动态地更换密钥。其核心思想是，对密钥引入混淆变换得到白盒密钥，每次加密时将白盒密钥和明文一起作为输入参数，进行查找表操作，最终得到输出结果。每次更换密钥后，只需更换白盒密钥。

动态白盒使用流程分为初始化和加（解）密2个过程，如图1 所示。

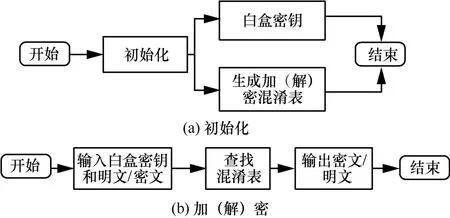
图1 动态白盒使用流程

初始化过程涉及表的生成和白盒密钥的生成，加（解）密通过查找混淆表实现。

动态白盒算法的实现流程为，对轮密钥和数据进行行变换操作，然后乘16×16的非退化矩阵（称该操作为L变换），从而实现线性混淆。对混淆后的结果进行异或操作、S盒变换、列混淆操作，最后乘32×32的非退化矩阵（称该操作为R操作）。

涉及的表为行变换表（对应行变换和L变换）、加密钥表（对应加密钥操作ARK）、列混淆表（对应S盒变换、列混淆操作MC 和R变换）。引入的L变换和R变换在相邻的表之间抵消。

以AES-128 为例进行说明，通过改变轮与轮之间的边界，并且将行变换操作提前。修改后的轮边界如图2 所示。下面，将描述密钥变换和各表的构造过程。

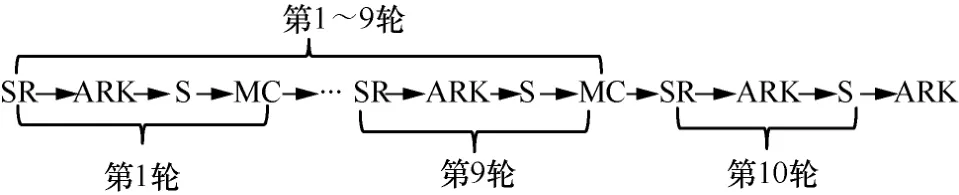
图2 修改后的轮边界

1)密钥变换

首先对AES 密钥进行密钥扩展操作，得到轮密钥。密钥变换的过程可描述如下，以第r（1≤r≤10）轮为例。首先将轮密钥进行变换操作。然后将密钥矩阵的每一列分成两部分，每2 B 为一组，得到GF(2)16上的列向量，对其进行线性变换：随机生成16×16的非退化矩阵Li(i≤0 ≤7)，计算

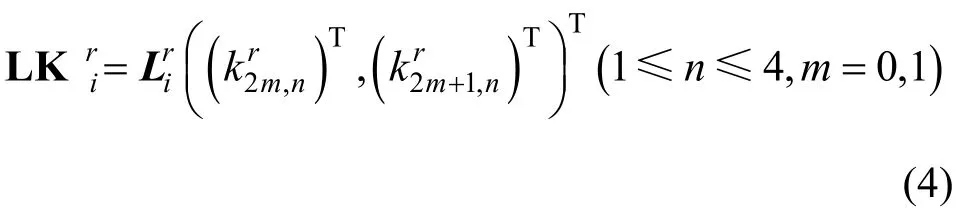
图3 密钥变换

由于AES 进行最后一次加密钥操作后不进行行变换，因此，不对最后一次的轮密钥进行行变换操作。对密钥矩阵进行线性变换的过程可以写成

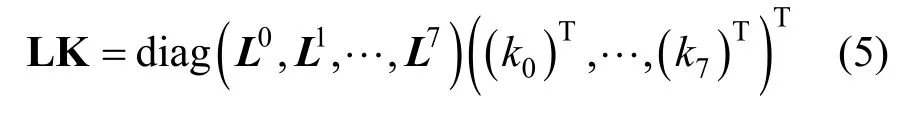
其中，diag 表示对角阵。下面以加密的过程为例，描述查找表的生成方法。按照顺序被查找的表依次为输入变换表、行变换表、异或辅助表、加密钥表、列混淆表和输出变换表。为了更清晰地描述动态白盒实现的过程，将行变换表放到列混淆表后面进行说明，输入输出变换表放到最后进行说明。

2)加密钥表

加密钥表对应加密钥操作。对于动态白盒实现，密钥是可变的，由于密钥和明文一样是作为参数输入的，若将其嵌入其他表里，则会导致表过于庞大，为此，单独构造16 bit 输入、8 bit 输出的加密钥表。其中，16 bit 的输入包含8 bit 白盒密钥和8 bit 明文。这里的白盒密钥是由密钥变换过程生成的。

表构造过程为，对8 bit 白盒密钥和8 bit 明文先解码，再进行异或操作得到8 bit 的数据；然后对8 bit 数据进行输出编码：先进行线性变换，再进行非线性编码得到输出数据。加密钥表如图4 所示。

图4 加密钥表

3)列混淆表sTMC

与文献[6]中的nTMC 表构造思路相同，为了减少表的大小，将列混淆操作分成2 步，先是将列混淆矩阵MC 分割后和状态矩阵的列相乘，最后将分割相乘的结果再相加，即

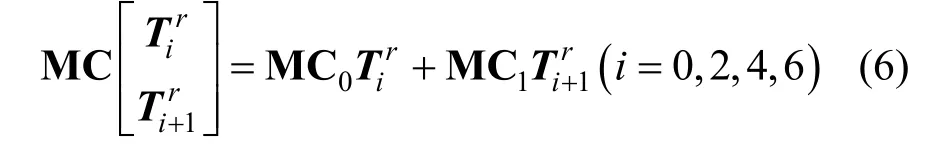
其中，将MC 进行矩阵分块，分成2 个32×16的矩阵，即MC=(M C0,MC1)，对状态矩阵分块，得到Tir。

列混淆表sTMC 实现了乘分割后的MC 矩阵：每个sTMC 表乘MC 的一部分，每轮一共有8 个sTMC 表。由于加密钥表的输出数据含有线性变换，因此将S盒置换嵌入列混淆表里而不是加密钥表，sTMC 表列混淆表的输入为16 bit，输出为32 bit。输入的状态矩阵每2 B 为一组，分成8 组，分别查找8 个sTMC 表，得到8 个32 bit 的向量，后面两两一组进行异或，最后得到128 bit 数据。

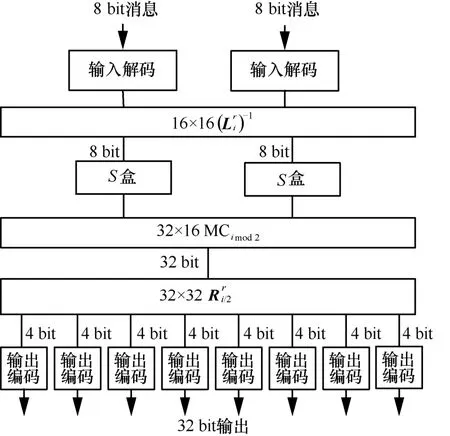
图5 列混淆表第1～9 轮

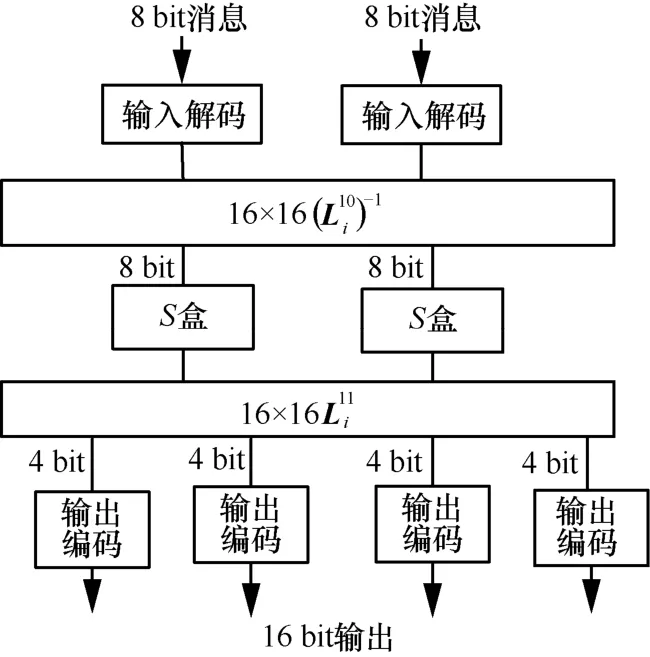
图6 列混淆表第10 轮

4)行变换表

行变换操作可以看作对一个128 bit 的列向量乘128×128矩阵的变换，行变换操作可使用查找表的方式来实现。其涉及的线性变换如式(7)所示。

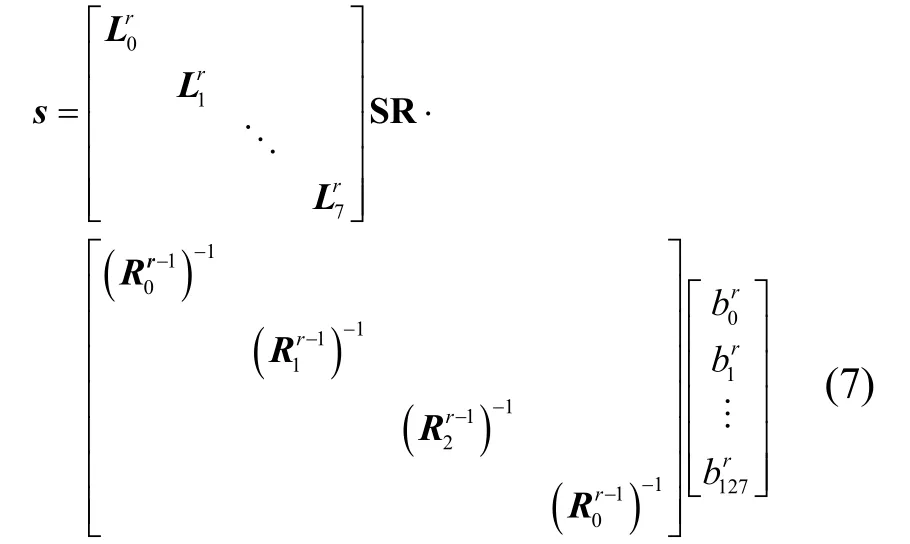
若不进行矩阵分割，行变换表大小为 2128×128 bit，这在实际中不可行。因此需要进行分割，GF(2)128上的任一列向量X可分割成32 块，其中每块为GF(2)4上的列向量。即xj(0≤j≤31)为GF(2)4上的列向量，则式(8)成立。

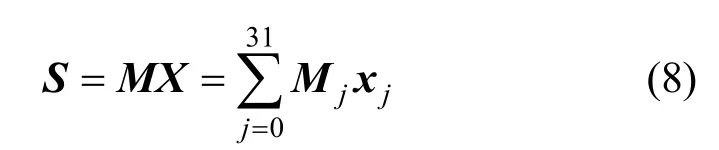
其中，M=(M0,M1,…,M31)为128×128的矩阵，Mj(0≤j≤31)为128×4的矩阵。

根据上述分割思路，可将一个 2128×128 bit 的表分割成32 个 24×128 bit 的表。下面进行具体说明。

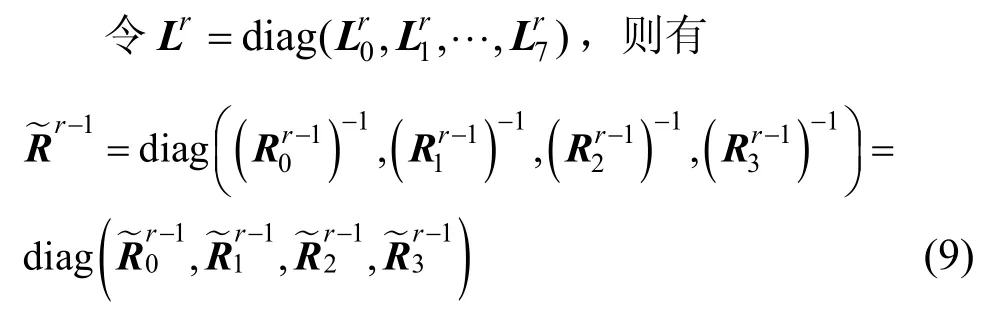
下面是行变换表的构造过程，行变换表的输入为8 bit，输出为128 bit。

输入的8 bit 数据，其中4 bit 来自乘MC0的结果，另外4 bit 来自乘MC1的结果。以状态矩阵的第一列为例，其中4 bit 是查找表之后的结果，另外4 bit 是查找之后的结果。在行变换表里，首先对输入数据做非线性变换，进行解码操作，将来源不同的4 bit 数据异或，得到4 bit 列向量；然后按照上述计算式，先乘32×4的矩阵，抵消列混淆表里的线性编码，再乘128×32的矩阵，进行行变换；最后乘128×128的矩阵，进行线性变换，得到128 bit 的列向量，其中每4 bit 一组，进行非线性编码，得到输出结果。表构造的过程如图7 和图8 所示，在查找第1 轮TSR 之前，先进行输入线性编码（乘大小为128×128随机矩阵IN），因此第一轮表的线性逆变换乘的是矩阵IN−1。

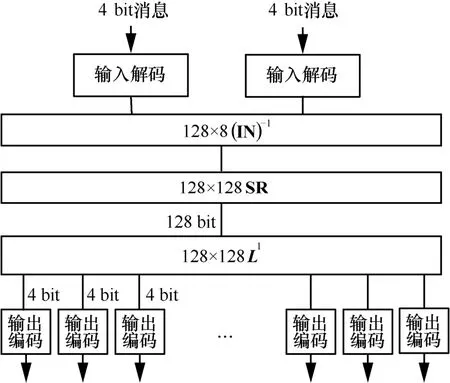
图7 行变换表第1 轮

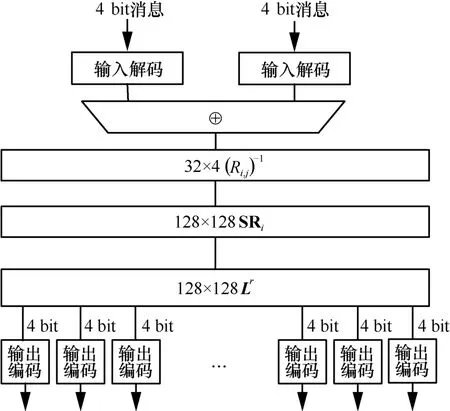
图8 行变换表第2～10 轮

5)异或辅助表TXOR

行变换的矩阵乘操作被分割成32 个列向量分别乘分割后的矩阵后再相加。本文用异或辅助表实现异或操作，一共有32 个乘法操作，对应32 个行变换表，每个表输出128 bit 列向量，因此行变换辅助表实现32 个128 bit 列向量的加法操作，对应31次异或操作。为了减少表大小，将31 次128 bit 异或操作分成31×32次4 bit 异或操作。异或辅助表如图9 所示。

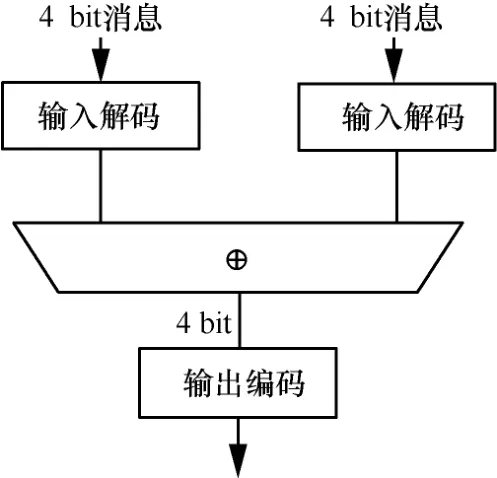
图9 异或辅助表

6)输入输出编码表

输入输出编码均是外部编码，输入编码是对输入明文进行乘128×128非退化矩阵IN，输出编码是对输出前的密文乘128×128非退化矩阵OUT，这里有

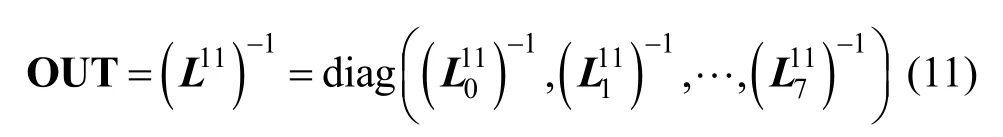
因此输入输出编码表实现了128×128的矩阵乘法，为了减少表大小，对矩阵进行分块，最终使用16 个规模为8×128的表来实现。表构造如图10所示。

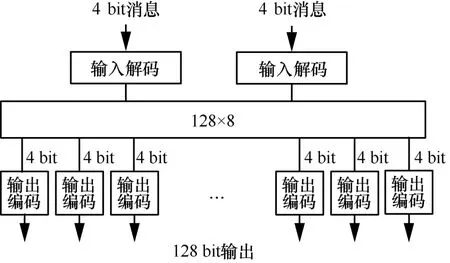
图10 输入输出编码表

整个加密过程为，首先查找输入编码表和辅助异或表实现输入编码，再重复10 轮如下的表查找：查找行变换表和辅助异或表实现行变换，查找加密钥表实现加密钥，查找列混淆表实现列混淆和S 盒变换。10 轮之后，查找加密钥表实现最后一轮加密钥，最后进行输出编码变换得到真正的密文。

4 正确性和效率分析

第3 节详细介绍了动态白盒实现方案，把AES实现的各步骤都使用查找表来实现，每个表的输入和输出都引入了线性变换和非线性变换来实现混淆，为了保证算法的正确性，在相邻表之间引入的变换都是互逆的，即保证了在进行AES 的各步骤之前的数据都是正确的。为了实现动态白盒算法，预先对轮密钥进行线性和非线性变换，其中非线性变换在加密钥表的输入里被抵消，而线性变换则和输入数据的线性变换相同，并在列混淆表中被抵消。各表的构造示意和描述均在第3 节给出说明。

下面，将分析动态白盒算法的效率。

TSR 第1 轮表的大小为 28×128 bit，表个数为16 个，对应TXOR 表个数为480 个；第2～10 轮，每轮需要32 个表，表大小为 24×128 bit，对应TXOR表个数为992 个。sTMC 表第1～9 轮表大小为216×32 bit，每轮需要8 个表；第10 轮表大小为216×16 bit，需要8 个表。TK 表大小为 216×8 bit，每轮需要16 个表。输入输出编码表大小为 28×128 bit，表个数为32 个，对应TXOR 表个数为960 个。各表所占空间总大小如下。

表1 3 种基于查找表的白盒方案的效率对比

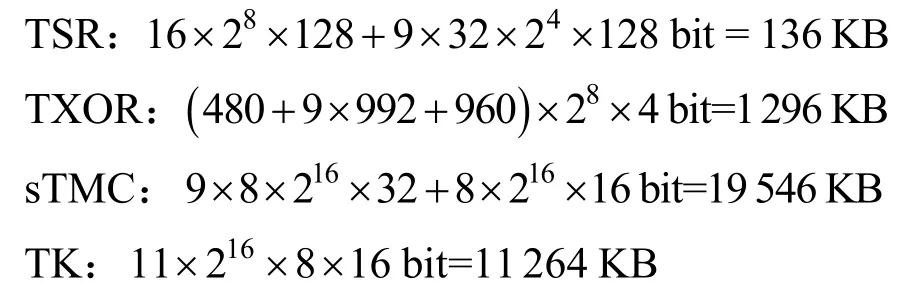
输入输出编码：32×28×128 bit=128 KB

因此，整个加密过程中所有表的大小为136+1296+19 456+11264+128=32 280 KB。

3 种基于查找表的白盒方案的效率对比如表1 所示。在3 种白盒实现里，只有Xiao-Lai 的白盒实现涉及了耗时多的矩阵乘法，其余均为简单的查找表操作。考虑到空间大小，DWB-AES 所占用的空间是最大的，但仍在可接受范围内，并且由于DWB-AES 是动态白盒，每次更换密钥需要更换查找表的大小为0。

此外，3 种基于查找表的白盒实现里，只有DWB-AES 既能抵御BGE 攻击又能抵御Mulder 等的攻击，这将在后面的安全性分析中进行说明。

5 安全性分析

下面，使用常用的分析方法对DWB-AES 进行安全性分析型。

5.1 本地安全性

查找表技术通过将密钥隐藏在表中，对表进行混淆，最终保证表空开后也无法对外泄露信息[1]，并且保证任何一个表都不会泄露额外信息，也就是所谓的本地安全性。DWB-AES 生成每个表的过程中，都引入了随机的线性变换和非线性编码，每一个查找表都独立引入了随机混淆信息，因此所有的查找表都是本地安全的。

5.2 白盒多样性和白盒含混度

Chow 等提出了评估白盒安全性的2 个指标，即白盒多样性和白盒含混度。白盒多样性用来评估可选择的混淆表的数量；白盒含混度用来评估给定表可选择的混淆编码的数量。白盒多样性越大，含混度越高，则密钥混淆的越充分，越不容易被提取密钥。

GF(2)上的n×n阶可非退化矩阵的个数为，m×n列满秩矩阵的个数为例如GF(2)上的4×4非退化矩阵个数为20 160，由此计算本文白盒实现中表的白盒多样性。

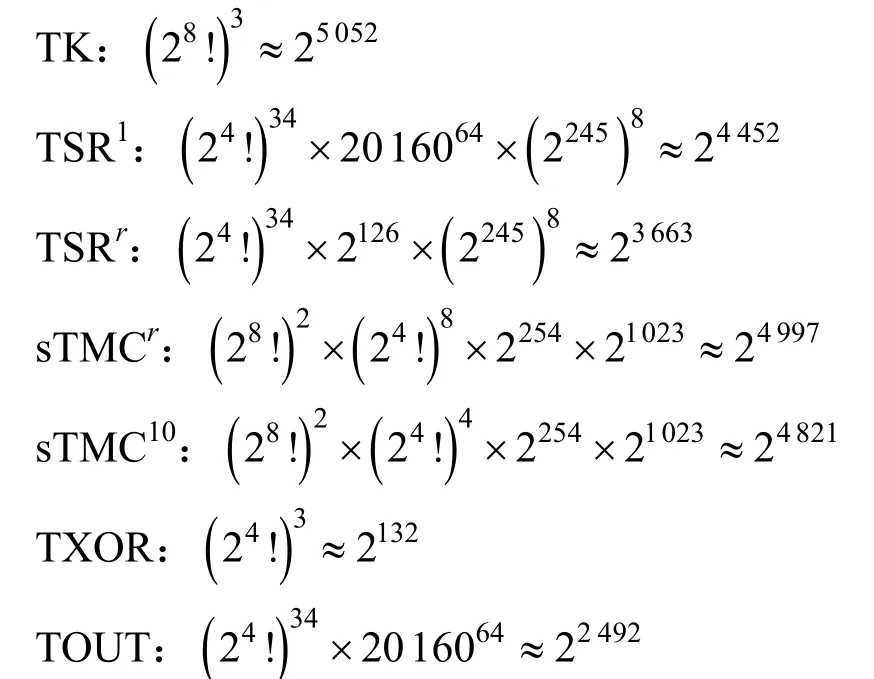
表2 给出了3 种白盒方案的白盒含混度和白盒多样性。TK 的白盒含混度为 28!×28≈21692，TXOR 的白盒含混度为 24!×24≈248，其余表的白盒含混度计算起来比较复杂，本文仅给出粗略的下界，TSR 为(24!)2×2126≈ 2214，sTMC 为 (28!)2×2254≈23622，TOUT 为 (24!)2×2016032≈ 2536。

表2 3 种白盒方案的白盒含混度和白盒多样性

从表2 可以看出，DWB-AES 拥有较高的白盒含混度和白盒多样性，因此具有较高的安全性。

5.3 抵御BGE 攻击

Billet 等提出了对Chow 等的白盒AES 算法的攻击方法，被称为BGE 攻击。在Chow 的白盒设计里，表满足了比较高的白盒多样性和白盒含混度，从单个表里提取密钥信息十分困难，然而由于表与表之间的混淆会相互抵消，将表组合在一起分析能更容易地提取密钥信息。在BGE 攻击中，将每轮的各变换当作一个整体，看作一个变换，如图11 所示。从图11 可以看出，每轮的输入编码和前一轮的输出编码是互逆的，即

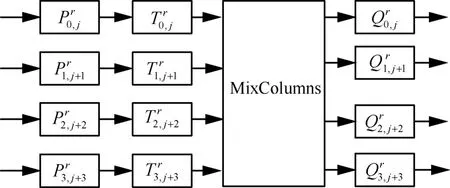
图11 Chow 等白盒算法流程

其次，计算出仿射变换，该步骤主要基于任意的(yi,yj)存在线性关系，即yi(x0,00,00,00)=

下面，将说明DWB-AES 可以抵御BGE 攻击。与Chow 等白盒算法不同，DWB-AES 的算法实现里，每一轮的置换编码是16 bit，(yi,yj)不一定存在线性关系。显然，将TK、sTMC 和TSR 组合在一起分析，是最容易攻击的。令输入数据为(x0,x1,…,x15)，令状态矩阵的排列方式为按列排列。将第一轮TK 表数据输入的第i个字节定义为xi，将第二轮行变换输出（查找TSR 和XOR 表的输出）的第i个字节定义为yi。令

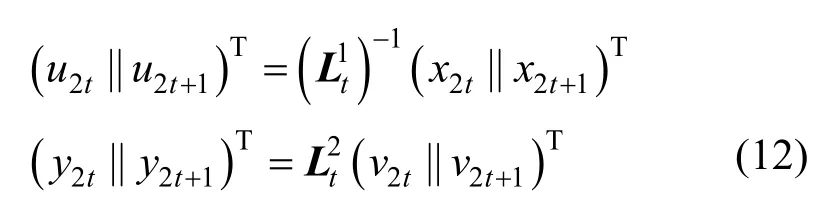
其中，t=0或 1，v是u经过加密钥、S盒变换、列混淆、行变换之后的结果。以前2 B 为例，第1 B的v0和v1的计算式为

5.4 抵御Mulder 攻击

Mulder 等[7]对Xiao-Lai 白盒实现进行了攻击，该攻击方法是基于Biryukow 等[19]的LE 算法。LE算法给出了寻找线性变换对(A,B)，使S2=B◦S1◦A的算法，其中S1和S2均为nbit 双射，若存在这样的线性变换对，则S1和S2是线性等效的，此时LE 算法输出符合要求的线性变换对集合；否则，输出相应信息表示S1和S2不是线性等效的。在Xiao-Lai 白盒实现里，由于TMC 表只引入了线性变换

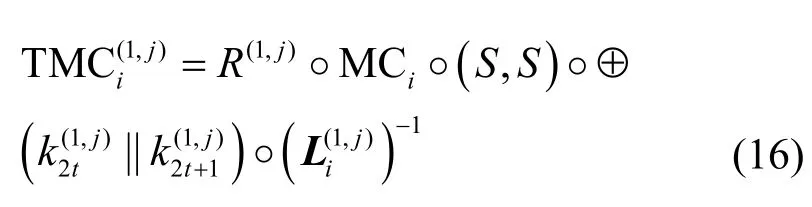
其中，(S,S)为AES 的S盒变换。因此若找到TMC和(S,S)之间的线性变换(A,B)，则可将表中引入的线性变换去掉，进而提取密钥。

Mulder 等通过观察Xiao-Lai 白盒实现结构，对LE 算法进行改造，以便能在 232的复杂度内提取密钥。首先，Mulder 等将密钥相关的表转换为密钥无关的表。其次，找到线性矩阵。最后，提取AES 密钥。其中，找到线性矩阵的步骤是核心步骤，通过将第1 轮的TMC 表和第2 轮的列混淆操作结合，并将列混淆操作相关输出设置为0，攻击者可以构造出线性等价解的集合。

下面将说明这种攻击方法不适用于DWB-AES。由于表的输入和输出均增加了非线性编码，因此使用基于LE算法及Mulder等的改造算法来寻找线性变换对(A,B)的方法不能直接被应用。即使将非线性编码的部分去掉，由于TSR 表的输入分别来源于列混淆矩阵MC 和TMCi+1，线性等价的解集合的构造将更加复杂。

该集合的大小为 224，而不是原来的 28，这将攻击复杂度提升至 264，对于使用白盒密码的应用程序来说，可认为是安全的复杂度。

本文使用常用的方法对DWB-AES 进行了安全行分析，并对Chow 白盒方案、Xiao-Lai 白盒方案和DWB-AES 进行了对比，结果如表3 所示。

表3 3 种白盒方案对比

6 结束语

针对物联网设备软硬件资源有限，密码模块既要满足安全性，又要具有较大灵活性的需求，本文提出了一种不需要更换查找表就能更换密钥的动态白盒实现方法DWB-AES，在保证正确性的前提下，具有较高的安全性，可以有效地抵御BGE 攻击和Mulder 等针对白盒算法的已知常用攻击，由于该方法在密钥更新时不需要更换查找表就能更新密钥，因此应用模式更加灵活，可以更好地满足物联网设备在安全应用中的需求。