物联网数据收集中无人机路径智能规划

付澍，杨祥月，张海君，陈晨，喻鹏，简鑫，刘敏

（1.重庆大学微电子与通信工程学院，重庆 400030；2.重庆大学信息物理社会可信服务计算教育部重点实验室，重庆 400030；3.北京科技大学计算机与通信工程学院，北京 100083；4.北京邮电大学网络与交换技术国家重点实验室，北京 100876）

1 引言

近年来，物联网产业的飞速发展，极大地推动了无线传感器网络（WSN,wireless sensor network）技术的应用，其承载的业务数据量呈几何式增长。WSN 中存在大量的数据需要被收集，根据收集方式的不同，可将其分为2 种类型，静态数据收集和移动数据收集。静态数据收集是指传感器网络中的节点通过自组网，将自身采集的传感器数据经过多跳上传到数据中心[1]；移动数据收集是指在被监测环境中设置一个可移动的数据收集器进行数据收集。针对部署在地表交通困难的大规模无线传感器网络，无人机提供了一种有效的方式来对传感器设备移动式地进行数据辅助收集[2]。

无人机是我国人工智能产业体系的重点培育产品。与静态数据收集方法相比，基于无人机的移动数据收集可以显著降低数据传输的能耗，减少多跳间数据路由中存在的隐藏终端及其发送冲突问题带来的射频干扰，并有效延长网络的使用寿命。

无人机数据收集克服了地面数据采集的局限性，但仍然有一些关键的问题需要解决。具体而言，无人机数据收集包括网络节点部署、节点定位、锚点搜索、无人机路径规划、网络数据采集5 个部分[3]。无人机最致命的缺点是续航时间短[4-6]，因此其能耗问题是系统稳定性的关键。近几年，关于无人机在数据收集的能耗研究中，无人机路径规划是一个开放性的研究课题，引起学术界的广泛关注。无人机路径规划是一个复杂的网络优化问题[7]，一般可分为全局路径规划和局部路径规划。

一般而言，无人机将在可用能量限制下，根据任务环境信息事先规划一条全局最优或次优路径，得到访问节点的访问顺序，再通过局部路径规划进行实时单个节点的搜索与逼近。近年来，无人机路径规划已经得到了广泛的研究。文献[3]把无人机路径规划问题建模成经典的旅行商问题，并执行快速路径规划（FPPWR,fast path planning with rule）。文献[8]利用马尔可夫链对单个无人机从远处传感器收集数据的移动过程进行建模，并模拟无人机运行过程中的不规则运动。文献[9]利用部分可观察的马尔可夫决策过程（POMDP,partially observable Markov decision process）对无人机路径进行规划。文献[10]基于Q 学习算法对无人机的路径和避障等问题进行学习，并采用自适应随机探测的方法实现无人机的导航和避障。文献[11-14]基于深度强化学习（DRL,deep reinforcement learning）实现无模型的无人机路径规划。除了利用机器学习方法外，研究者还提出了很多启发式算法[15-17]来解决无人机路径规划问题。

定向问题[18]为节点选择和确定所选节点之间最短哈密顿路径的组合，可以看作背包问题和旅行商问题2 种经典问题的组合。本文将无人机数据收集过程的全局路径规划问题建模为定向问题。本文考虑的全局路径规划是指综合考虑无人机自身的能量约束、节点收益等，在指针网络深度学习架构下进行的路径规划。其中，背包问题的目标是在可用资源限制下，选择一部分节点并使之获得的收益最大化；旅行商问题的目标是试图使无人机服务所选节点的旅行时间或距离最小化。

文献[19]对定向问题最近的变化、解决方案及应用等进行了综述。近几年，关于求解定向问题的启发式方法很多，例如遗传算法[20]、动态规划法[21]、迭代局部搜索法[22]等。

2015 年，Vinyals 等[23]在人工智能顶级会议NIPS 上提出了一个用于解决变长序列到序列的神经网络模型——指针网络，还验证了该模型可以单独使用训练示例来学习3 个几何问题的近似解，即寻找平面散点集的凸包、Delaunay 三角剖分算法和平面旅行商问题。指针网络深度学习被提出后，近几年被研究者多次引用，文献[24]将指针网络深度学习结合强化学习解决旅行商问题，并提出该模型也可用于解决背包问题。文献[25]使用指针网络模型结合强化学习技术来优化3D 装箱序列以最大化其收益。受这些模型的启发，本文首先将无人机全局路径规划建模为定向问题，接着采用指针网络深度学习对其进行求解。

在局部路径规划方面，无人机将根据节点广播参考信号强度（RSS,received signal strength）的特征[26]对其局部路径进行规划。文献[27]采用Q 学习利用无人机对非法无线电台进行定位和寻找。然而，传统Q 学习很难解决具有大量状态空间的模型，这导致其很难适用于大规模节点网络中的无人机路径规划。本文通过深度Q 网络（DQN,deep-Q network）学习机制对大规模的Q 表进行模拟与近似，从而极大地降低了Q 学习的计算复杂度。

综上，本文首先将无人机的全局路径规划建模为定向问题并通过指针网络深度学习求解；然后在局部路径规划方面，利用DQN 使无人机逼近目标节点。仿真结果表明，在无人机能耗限制下，所提方案能极大地提升物联网中的数据收集收益。

2 系统模型及问题建立

2.1 全局路径规划

本文综合考虑无人机在数据采集过程中面临的能量约束问题和路径规划问题。无人机能量消耗不仅与航行时间、航行速度有关，还与所处环境中的风速、障碍物等有关[28]。文献[29]将无人机的路由算法分类为恒定速度无人机、自适应速度无人机、悬停最大服务时间（HMS,hover with maximum service time）等。本文采用HMS 的路由方法，即无人机悬停在相应节点上方，并以最大悬停时间tmax对用户进行数据传输，且假设无人机以恒定的速度v飞行。

在图1 所示的系统模型中，无人机的起点和终点均为无人机服务站Ddepot。Ddepot可对无人机收集到的数据进行处理，并对无人机充电，需要收集数据的传感器节点随机分布在地图上，可通过聚类算法对随机分布的传感器节点进行分簇，并得到簇的中心坐标（图1 中黑点）[30]。关于无人机以什么样的顺序访问这些簇才能在有限的能量约束下取得最大收益的问题，可以被建模为一个定向问题，即选取点和确定最短路径2 种问题的结合。由于无人机数据收集存在无人机能量限制，因此不是所有的簇都会被服务。令S∈{1,2,…,k}表示簇的集合，其中k表示簇的数目。第i个簇的奖励值为pi，簇i到j的距离为disti,j，li,j=1表示i与j之间有路径，那么无人机全局路径规划问题可以表示为

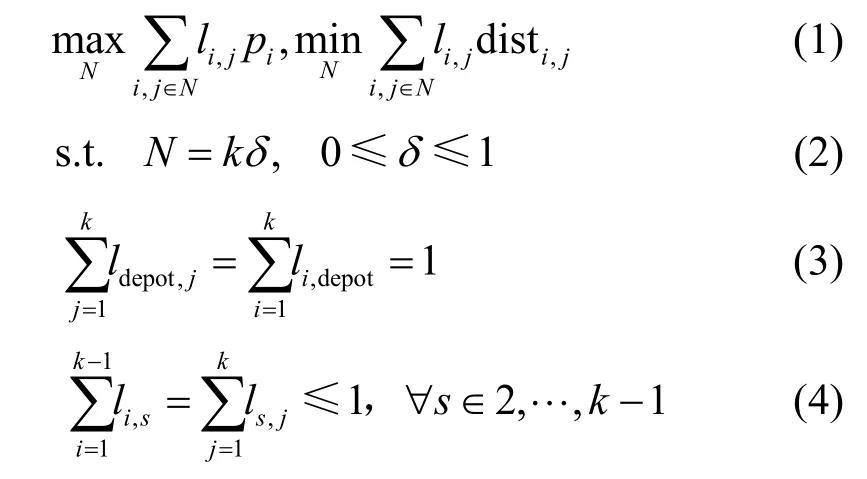
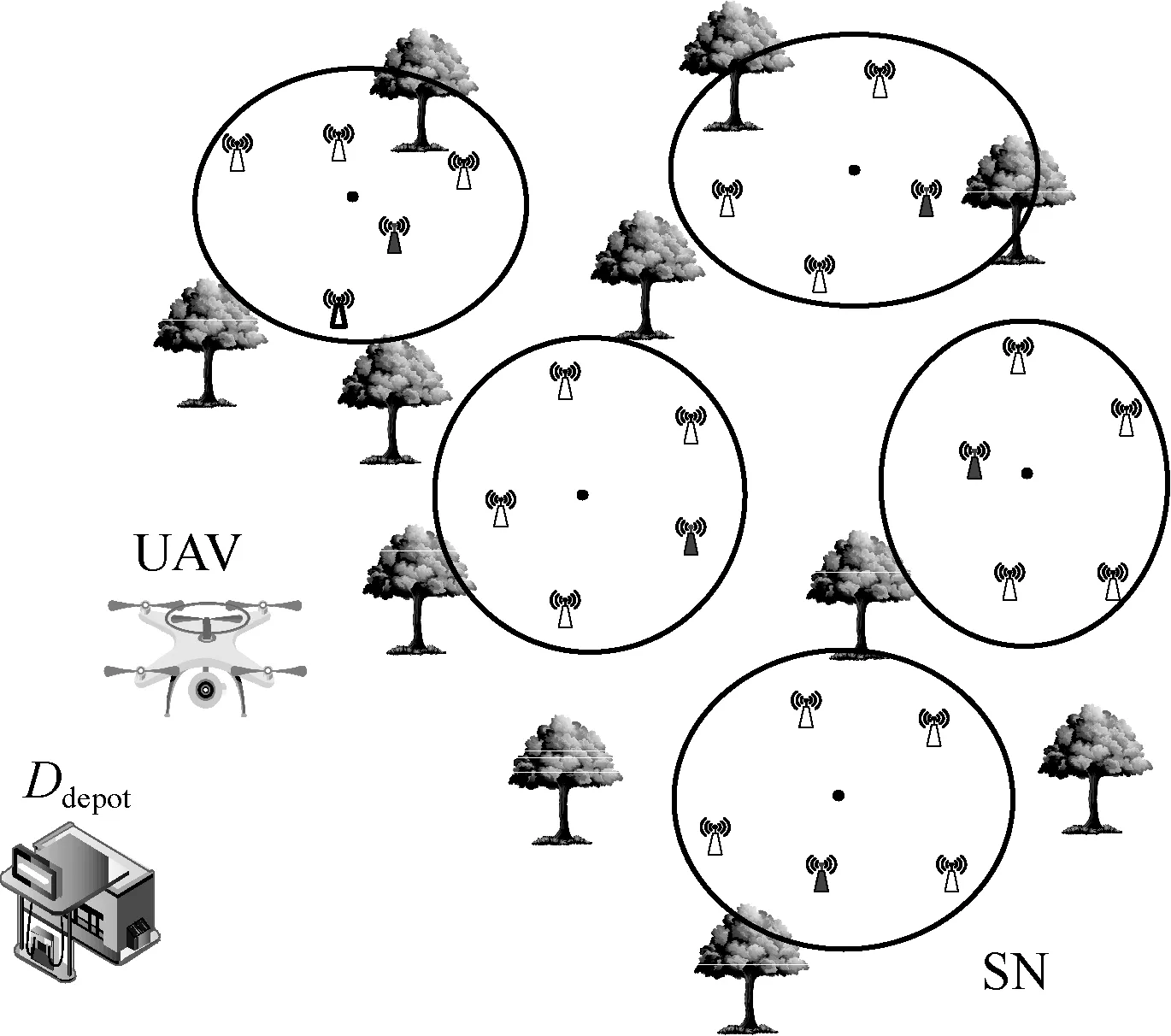
图1 系统模型

目标方程(1)表示最大化数据收集的奖励值，并且最小化无人机的飞行路径；约束(2)表示无人机可服务簇的份额；约束(3)表示起点和终点均为无人机服务站Ddepot；约束(4)表示每个簇最多被服务一次。

在优化目标式(1)中，关于每个簇奖励值的设定，如果简单设定为簇内所有节点存储数据的总和，则可能对稍远的节点不公平，所以可将每个节点的奖励值设置为

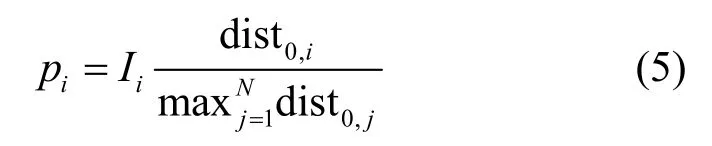
其中，Ii表示簇i内所有节点数据量总和的值（无量纲）。因此，奖励值的设定不仅与节点到服务站的距离有关，还与数据的存储量有关，且pi无量纲[31]。

2.2 局部路径规划

假设无人机对目标传感器的位置是未知的，无人机以固定的高度飞行，只考虑二维平面的运动，目标传感器节点的位置坐标为(x,y)，无人机当前状态的坐标为(xi,yi)，无人机与目标节点之间的距离可以表示为

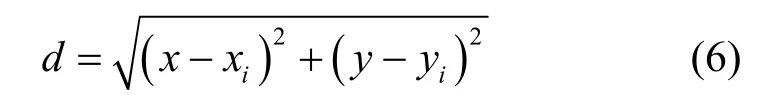
无人机通过配备天线来测量目标节点的RSS，无人机可移动方向被相等地划分为8 个方向，具体如图2 所示。

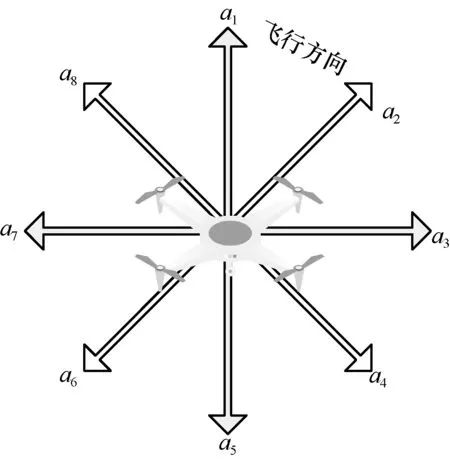
图2 无人机移动方向

RSS 值PR可以通过以下计算式求得，它与距离d（单位为m ）有关，具体为

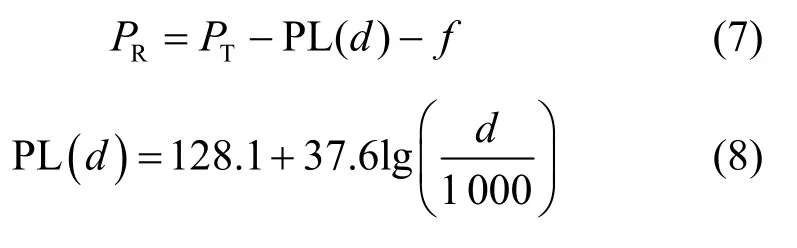
其中，PT为目标节点发射功率；PL(d)为距离d处的路径损耗，此处的路径损耗模型[32]采用3GPP TR 38.814，本文主要参考天线接收信号强度值，为简化系统模型，只考虑了地对地大尺度信道衰落，后期研究无人机数据传输过程中将进一步同时考虑视距和非视距对传输性能的影响[33-35]；f为捕获信道衰落变量。

深度Q 学习[36]融合了神经网络和Q 学习的方法，属于强化学习的一种，当然也应该具有强化学习的基本组成部分，即智能体、环境、动作、奖励、策略、值函数等。强化学习智能体与环境的交互过程如图3 所示。智能体通过与环境进行交互，循环迭代产生新的状态并结合环境给出奖励值。

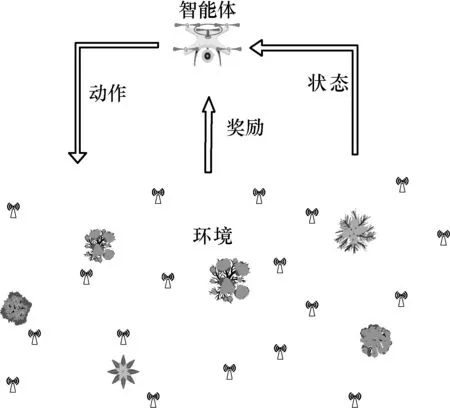
图3 强化学习智能体与环境的交互过程

Q值函数更新式为

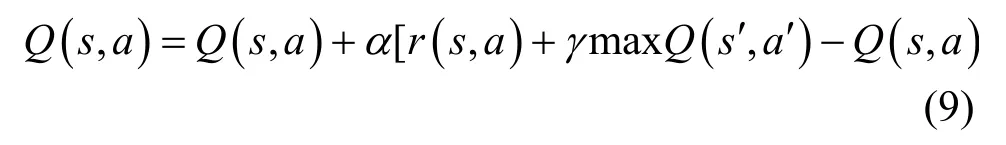
其中，α∈[0,1]是学习率，γ∈[0,1]是折扣因子。

无人机的状态s取决于各个方向测量的平均RSS 值中最大的RSS 值，动作空间对应图2 中的8个方向，即a∈{a1,a2,a3,a4,a5,a6,a7,a8}。奖励值r(s,a)的设定为：如果当前位置各个方向测量的平均RSS 值中的最大值减去上一位置的各个方向测量的平均RSS 值中的最大值为正，则给一个正的奖励值，该奖励值设为固定值；如果为负，则给一个负的奖励值。如果无人机达到终止条件，则给其较大奖励值，本文中奖励值设定为

无人机的终止条件为当距离d＜7.0 时，目标节点定位成功。深度Q 学习的原理框架如图4 所示。

3 算法建立

3.1 指针网络深度学习建立

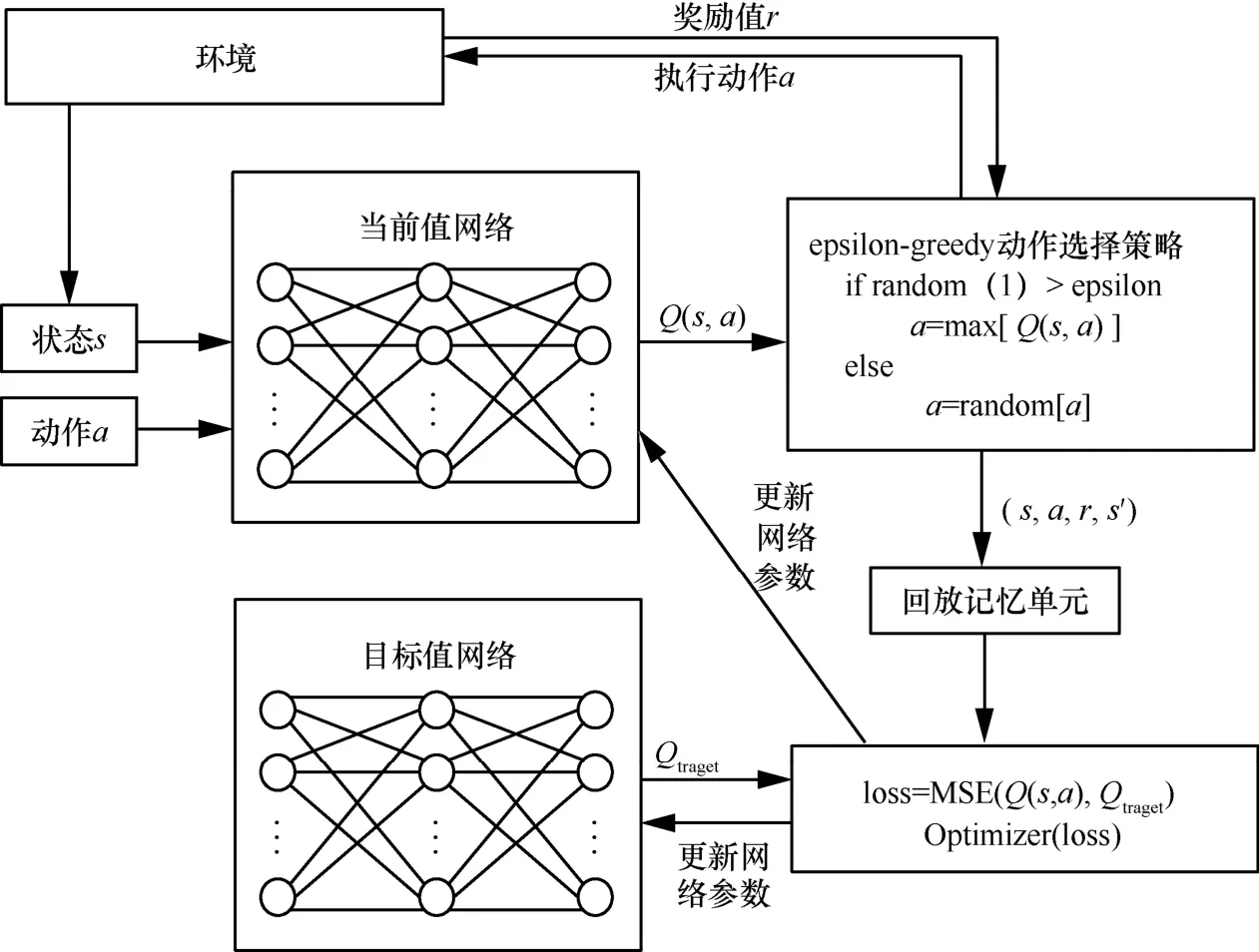
图4 深度Q 学习的原理框架

指针网络深度学习的结构如图5 所示，它是由序列到序列模型[37]和注意力机制[38]结合改进得到的，由Encoder 和Decoder 这2 个阶段组成。在Encoder 阶段，只考虑输入xj对输出yi的影响；在Decoder 阶段，解码输出注意力概率矩阵，并通过softmax 得到序列的输出概率分布。由于长短期记忆网络（LSTM,long short-term memory）[39]能够成功学习具有远距离时间依赖性数据的特征，其被用作网络单元构建指针网络深度学习模型。Encoder部分使用LSTM 多层神经网络（记为LSTM-e），Decoder 部分使用LSTM 多层神经网络（记为LSTM-d）。

图5 指针网络深度学习的结构

第2 节对无人机路径规划问题进行了建模，分别确定指针网络（PN,pointer network）深度学习模型的输入输出如下所示。

1)输入

Dcoords={(x0,y0),(x1,y1),…,(xk,yk)}为无人机服务站Ddepot和每个簇中心坐标Dloc的并集。假设Ddepot处的奖励值p0=0，Pprize={p0,p1,…,pk}为p0和pi的并集，Dinputs={(x0,y0,p0),(x1,y1,p1),…,(xk,yk,pk)}。

2)输出

输出序列Droads={P0,P1,…,Pn}表示无人机数据收集过程中簇的收集顺序，Pn对应Dinputs值的索引。指针网络深度学习的编解码过程为：输入序列Dinputs经过k+1 步依次输入Encoder 模块，然后通过Decoder 模块依次输出Droads中的元素。

因此指针网络的原理可以表示如下[40]。

编码过程。将输入序列Dinputs经过k+1 步依次输送给LSTM-e，得到每一步输入所对应的LSTM-e网络状态ej(j=0,1,…,k)，如式(11)所示。当Dinputs输入完毕后，将得到的隐藏层状态Enc=(e1,…,ei,…,en)进行编码后输入解码模块。

解码过程。由式(12)计算出LSTM-d 网络的隐藏层状态Dec=(d1,…,di,…,dn)；由LSTM-e 网络的隐藏层状态(e1,…,ei,…,en)和LSTM-d 网络的隐藏层状态Dec=(d1,…,di,…,dn)分别计算出每个输入对当前输出带来的影响，如式(13)所示。将其softmax 归一化后得到注意力矩阵ai，如式(14)～式(16)所示。然后选择矩阵中权重占比最大的指针作为输出，如式(17)所示。

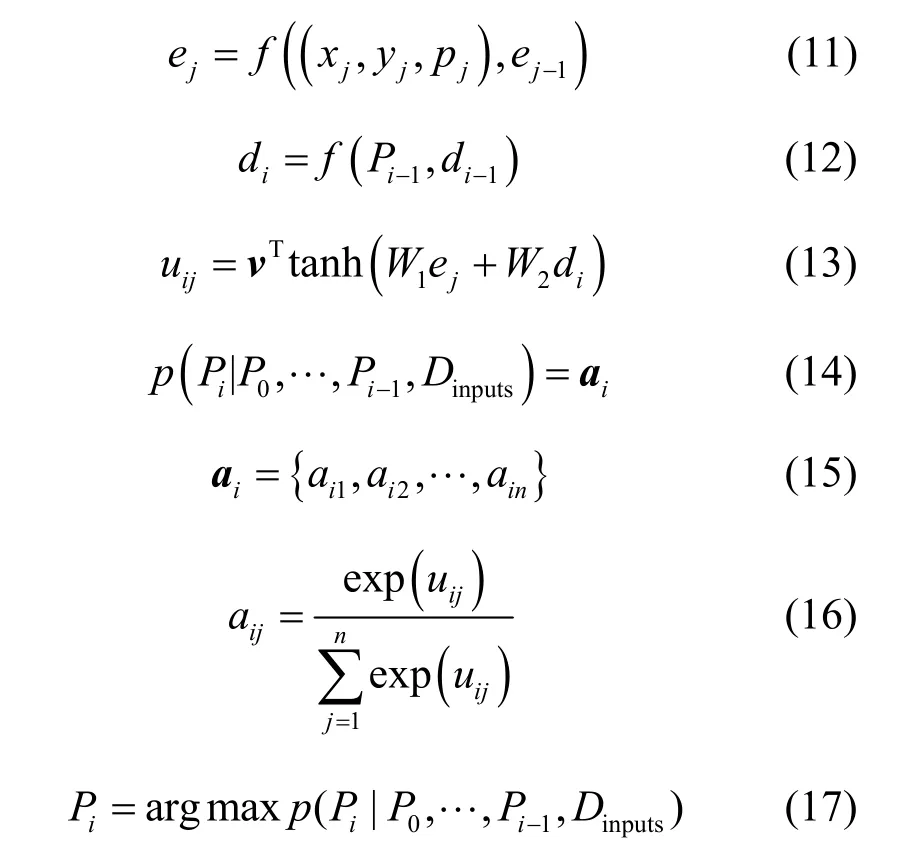
其中，f为非线性激活函数；v、W1和W2为输出模型的可学习参数；aij由uij经过softmax 后得到，其作用是将uij标准化为输入字典上的输出分布[23]。

在解码过程中，还要考虑到定向问题模型中的约束问题。首先，对于约束(2)，预设一个服务份额值δ。对于约束(3)，无人机的起点和终点均为无人机服务站Ddepot，因此，第一步和最后一步将P0和Pn设置为0。对于约束(4)，根据禁忌搜索的思想，在每一步添加Droads元素时，将其作为禁忌元素添加到Daction表中，每一步输出将根据Daction表，在注意力矩阵中选择非Daction表中权值最大的作为输出。

3.2 指针网络+主动搜索策略

根据文献[25]提出的主动搜索（AS,active search）策略，将Dinputs中的元素（除索引0 的位置）随机排列组合生成B个批次的输入序列，通过梯度下降法优化目标函数，最后输出路径。

通过多目标优化中的线性加权法将目标函数(1)改写成

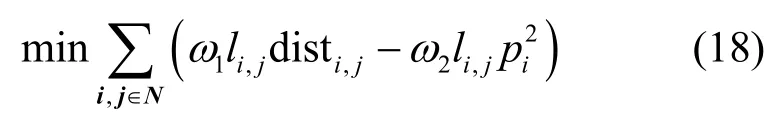
其中，ω1+ω2=1表示在减少无人机飞行距离与提升无人机服务奖励之间的折中关系，具体可由工程经验得到。本文设置ω1=0.9，ω2=0.1，通过梯度下降法，式(18)可以同时优化减小距离和增加奖励值。

指针网络+主动搜索策略的算法描述如下。

1)初始化输入序列，将Dinputs中的元素（除索引0 的位置）随机排列组合生成B个批次的输入序列。

2)将序列输入指针网络，得到一系列结果。

3)使用梯度下降法优化目标函数(18)。

4)重复执行步骤1)～步骤3)，直到达到终止条件。

5)选择最小的目标函数值的路径作为输出路径Droads。

3.3 DQN 算法建立

DQN 算法描述如下。

1)初始化经验重放缓存区。

2)预处理环境：把状态−动作输入DQN，返还所有可能动作对应的Q值。

3)利用ε贪心策略选取一个动作a，以概率ε随机选择动作，以概率1−ε选取具有最大Q值的动作。

4)选择动作a后，智能体在状态s执行所选的动作，得到新的状态s′和奖励r。

5)把该组数据存储到经验重放缓冲区中，并将其记作s,a,r,s′。

6)计算目标方程(10)，更新Q网络权重。

7)重复执行步骤3)～步骤6)，直到达到终止条件。

4 实验结果与分析

4.1 参数设置

为验证指针网络模型对无人机全局路径规划的优化性能，实验主要对比了指针网络深度学习、基于主动搜索策略的指针网络深度学习方法。为了对比AS 方法的效果，本文设计贪婪奖励（GP,greed prize）方法与其进行比较。GP 方法受贪婪优化方法的影响，先贪婪地选择奖励值大小为前N簇的坐标，然后通过PN+AS 方法求这些簇的最短路径。

实验令无人机服务站Ddepot的坐标为（0,0），在[0,1]×[0,1]（单位为km）的范围内分别随机生成50 个簇和100 个簇的中心位置坐标，分别为D50和D100。每个簇的奖励值设定按照式(5)得到。

表1 和表2 分别给出了AS 方法和GP 方法使用的参数及其相应值。

表1 AS 方法使用的参数及其相应值

表2GP 方法使用的参数及其相应值

为验证DQN 的性能，本文主要分析Q 学习和DQN 这2 种方法在无人机数据收集中单个节点定位的仿真效果。为模拟无人机接收信号强度值，采用网格法确定当前位置距离目标节点的距离，通过式(7)和式(8)计算接收信号强度值，实现DQN 状态输入。本文主要对2 种方法迭代次数内的成功率、步数及其最优路径进行比较。2 种方法均使用ε贪心策略，在仿真中将无人机到目标节点的距离小于7 m 视为成功，为防止算法无限次迭代，将无人机步数大于200 步视为失败。仿真结果表明，DQN 的性能优于Q 学习，能够达到一个较高的成功率。DQN 仿真各参数的设置如表3 所示。

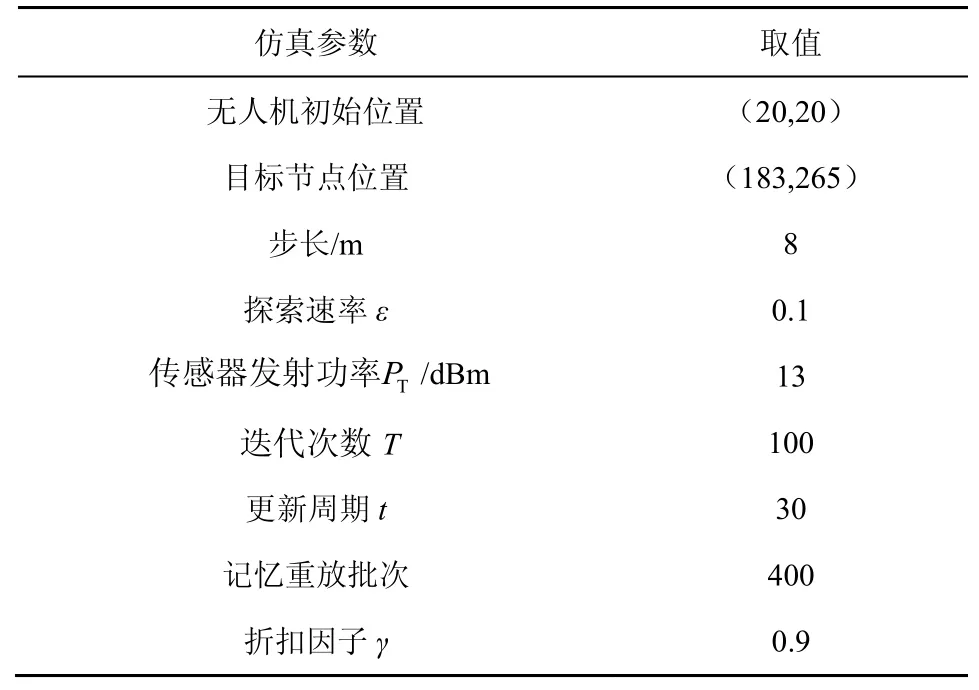
表3 DQN 仿真各参数的设置

4.2 结果分析

图6 和图7 分别是D50和D100下使用PN、AS和GP 的路径规划效果，表4 是D50和D100下使用PN、AS 和GP 的距离和奖励值，其中，距离的单位为km。根据式(9)可知，奖励值越大越好，距离越小越好，这样可以使模型的收益能效更高。从图6、图7 和表4 中可以直观地看出，使用PN 方法比AS 方法的路径规划图交叉点多，总路径距离大，总奖励值小；将GP 方法与AS 方法进行比较，GP方法交叉点少，总路径距离小，不过GP 方法存在贪婪的性质，相当于将全局路径规划问题变为一个简单的旅行商问题来解决，使该算法获得的奖励值更好，但在某些场景下有可能导致更大的飞行距离。虽然AS 方法不能完全达到GP 方法的效果，但AS 方法的效果接近GP 方法，且AS 方法最大的特点就是同时优化距离和奖励值，虽然奖励值可能不如GP 方法但其距离有可能更小，且更具随机性、更适合动态环境中的无人机路径规划。

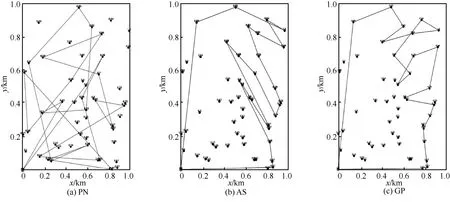
图6 D50下使用PN、AS 和GP 的路径规划效果

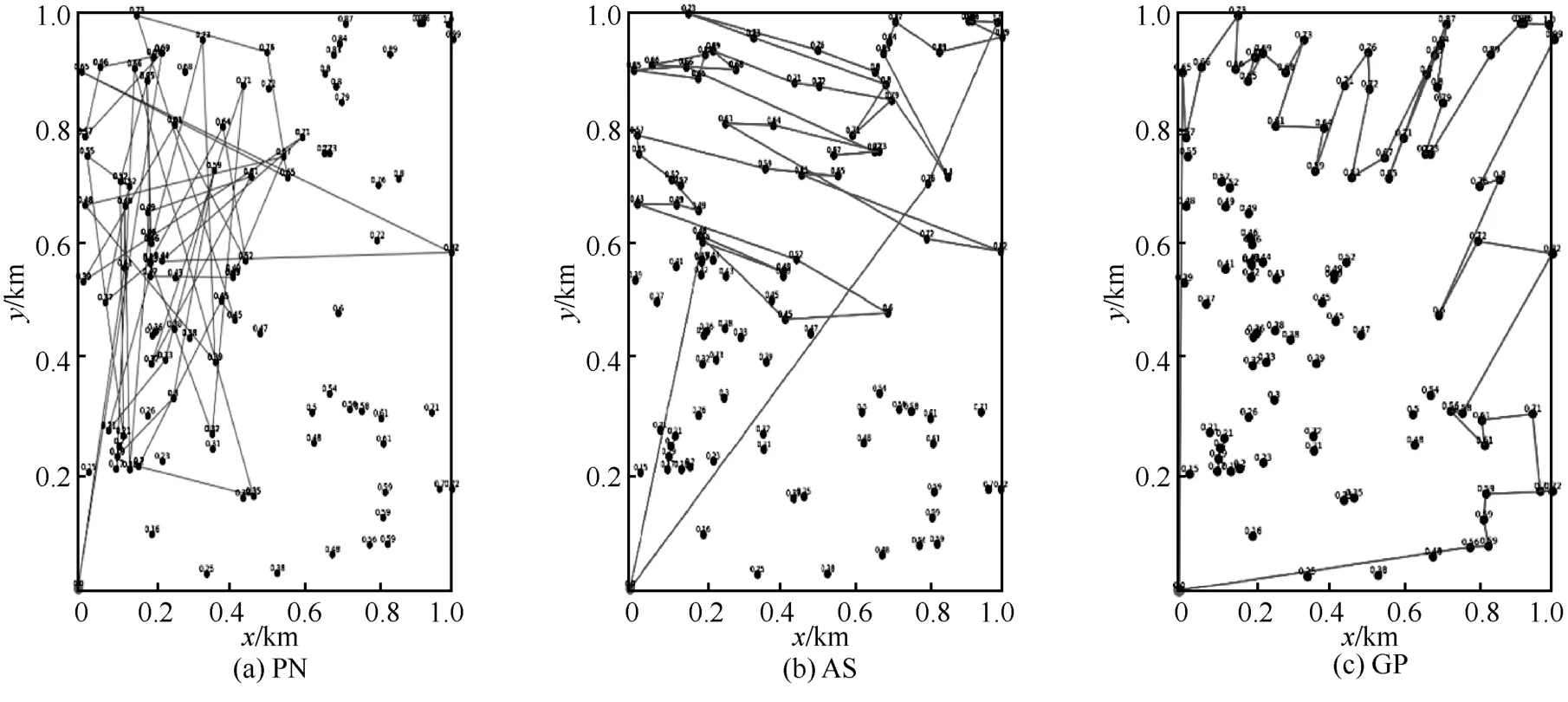
图7 D100下使用PN、AS 和GP 的路径规划效果

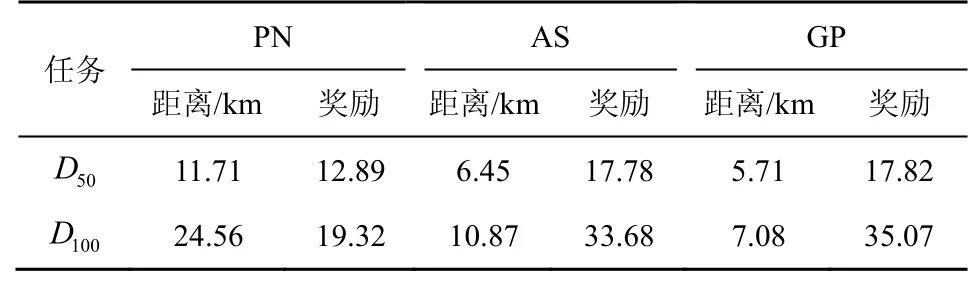
表4 D50和D100下使用PN、AS 和GP 的距离和奖励值

图8 是AS 方法下使用梯度下降法训练PN 的损失值。从图8 中可以看出，训练PN 的损失值随着迭代次数的增加先快速下降，而后趋于稳定，在0 值上下波动，这表明该深度模型可以在训练后达到收敛，网络性能可靠。

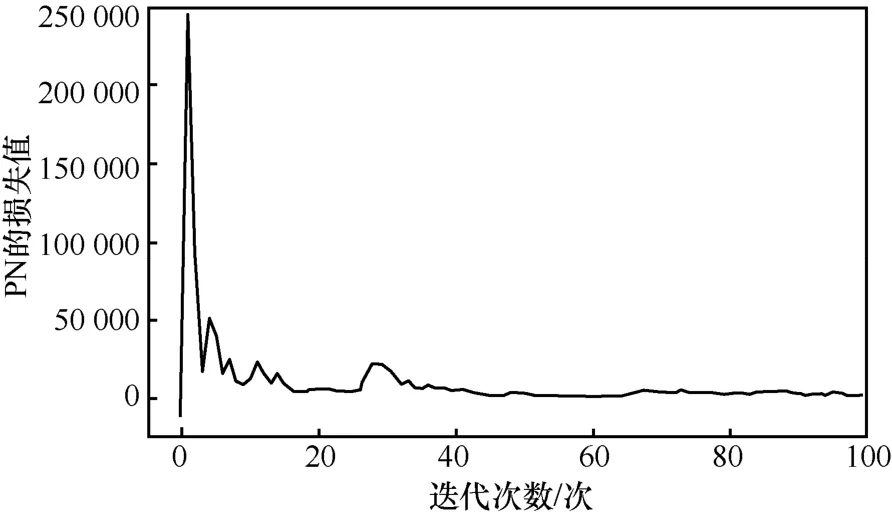
图8 AS 方法下使用梯度下降法训练PN 的损失值

图9 为DQN 和Q 学习的成功次数的步数变化波动曲线。从图9 中可以明显看出，DQN 步数的变化只在一开始波动较大，经过一个更新周期（30 次）后波动趋于平稳，且步数较小，迭代次数为100 次，成功率接近100%；Q 学习的成功次数只有7 次，其余均大于200 步。

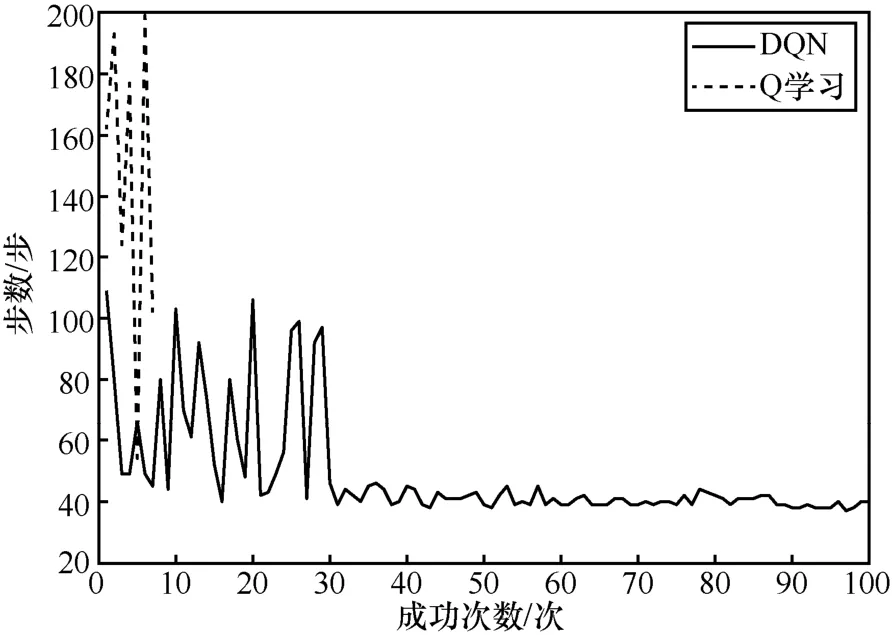
图9 DQN 和Q 学习成功次数的步数变化波动曲线

从图10 可以更清晰地看到，DQN 的最优路径与Q 学习的最优路径相比更平缓、拐点较少。表5 为不同起点和目标位置时Q 学习和DQN 的最优步长比较。从表5 可以看出，针对不同起点和目标位置，除了第三组（0,0）→（68,78）这2 种方法效果一样外，其余场景中的DQN 都优于Q 学习，可见DQN 的泛化性能强，可以适应不同的场景。

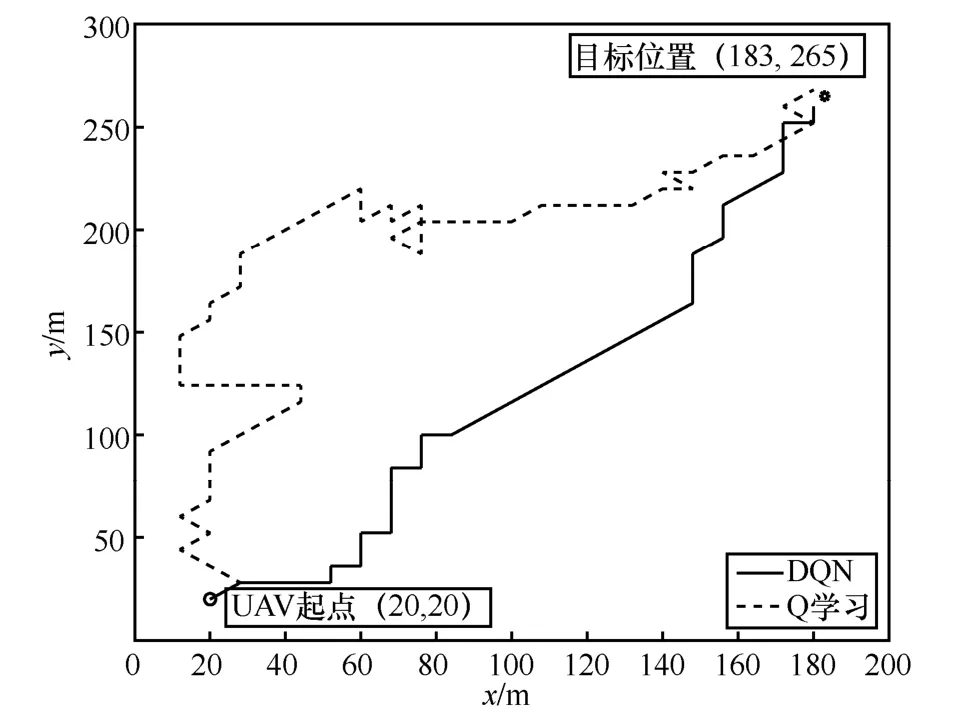
图10 DQN 和Q 学习最优路径对比

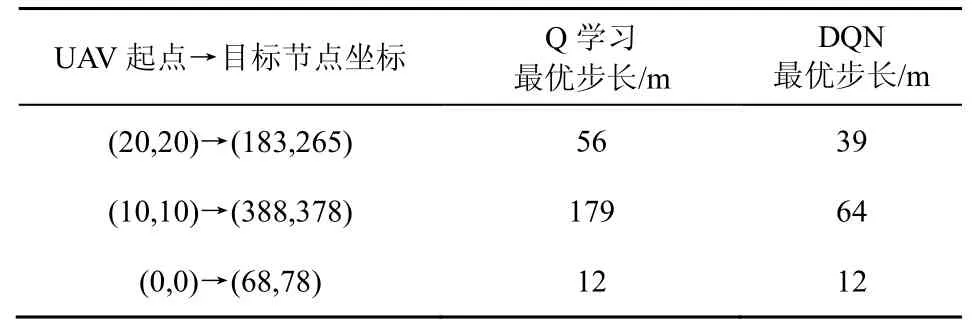
表5 不同起点和目标位置时DQN 和Q 学习的最优步长比较

5 结束语

本文首先使用指针网络深度学习来解决无人机数据收集过程中的全局路径规划问题，并将该问题建模成定向问题，利用指针网络深度学习得到无人机服务节点集合及服务顺序。然后，根据无人机接收目标节点的RSS 通过DQN 来定位目标节点并接近目标节点，经仿真验证，DQN 在时延等方面的性能优于Q 学习。最后，通过仿真验证了所提学习机制的有效性。