基于相对熵和K-means 的形状相似差分隐私轨迹保护机制

朱素霞，刘抒伦，孙广路

（哈尔滨理工大学计算机科学与技术学院，黑龙江 哈尔滨 150080）

1 引言

随着智能手机和5G 网络的普及，移动设备可以运行更复杂的程序，并以更快的速度、更低的时延传输信息，这为物联网的发展提供了坚实的基础。物联网中基于位置的服务（LBS,location-based service）[1-2]从仅应用于导航类软件，到逐渐应用于社交、游戏等产品，目前已应用于越来越多的领域。由于LBS 要求用户将位置数据提供给相应的服务提供商或第三方数据提供者，因此如何保护用户的位置隐私成为LBS 的主要关注点[3]。数据在向服务商提交的过程中涉及网络传输、数据采集等多重隐私泄露风险，用户的隐私信息可能会随着轨迹数据的发布而被泄露。轨迹隐私信息一旦暴露，用户将遭受的最大威胁便是敏感位置泄露，这可能导致攻击者获取用户的真实地理信息，并根据背景知识推测出用户地理轨迹，进一步获得兴趣爱好、行为习惯等重要用户隐私信息。文献[4]中记载了30 个基于位置应用中有15 个应用[5]泄露用户的位置信息给攻击者或分析服务器。文献[6]表明MySpace 有3.6 亿用户信息被泄露。文献[7]使用基于Twitter 社交网络应用数据分析了用户的敏感信息，如工作单位的具体位置等。因此，敏感位置信息的泄露可能会使用户处于不利的地位。

近几年，许多位置隐私保护机制被提出[8-9]，用于解决LBS 或持续的位置共享，而差分隐私因其具有严谨的数学基础，并严格定义了攻击者的背景知识，在轨迹保护研究领域受到了广泛的关注。但是，现有基于差分隐私的轨迹保护机制存在以下2 个问题。

1)现有连续轨迹保护机制可以保证轨迹的隐私性，但是大部分没有考虑不同位置因敏感度不同而需要不同的隐私预算。对轨迹中的不同位置分配相同的隐私预算，会导致隐私预算的浪费。例如，对不需要高强度保护的位置点分配了高强度保护对应的隐私预算，使该位置点被过度保护。使用相同的隐私预算对位置点进行保护，还会导致轨迹的可用性变差。例如，在不需要高强度保护的位置点进行高强度保护，因此分配给该位置点的隐私预算较小，使该位置点的噪声较大，从而导致轨迹的可用性变差。

2)大部分现有的隐私保护方法只考虑了轨迹的时间和空间对轨迹可用性的影响，忽略了轨迹的相似性对轨迹可用性的影响[10]。图1 中有3 条轨迹，分别为真实轨迹、干扰轨迹1 和干扰轨迹2，每条轨迹由4 个位置点组成。干扰轨迹1 和干扰轨迹2中的各个干扰位置到其对应的真实位置的距离都相同。干扰轨迹1 穿过了真实轨迹，形成了与干扰轨迹2 完全不同的干扰轨迹。当LBS 中用户发布的位置和干扰轨迹1 类似时，干扰轨迹就会不断穿过真实轨迹，这会对轨迹的可用性和真实性造成严重影响。在真实位置的隐私预算较小的前提下，干扰位置与真实位置距离较远，会出现该干扰点特别突出的情况。攻击者可以对轨迹数据采用噪声滤波等手段过滤异常轨迹、恢复真实位置，导致保护失效。如果用户发布的位置类似于干扰轨迹2，即使隐私预算较小，也会尽量使干扰轨迹与真实轨迹形状相似，不会使该干扰点被过滤掉而导致保护失效。

图1 条轨迹间形状的对比

针对上述两点问题，本文首先利用相对熵设计了一种位置敏感的隐私级别实时计算算法，根据发布位置的敏感度的不同，为不同敏感度的位置实时分配隐私级别；其次，将该隐私级别实时计算算法与本地化差分隐私相结合，建立σ−隐私模型；最后，提出了基于K-means 的形状相似差分隐私（DPKTS,differential privacy based onK-means shape similarity）轨迹保护机制，该机制在保证各个发布位置隐私性的前提下，通过聚簇与提高轨迹形状相似性，获得更好的轨迹可用性。

2 相关工作

针对LBS 中的敏感位置信息，研究者已经提出了很多隐私保护方法，依据采用的核心思想可将其大致分为4 类，即泛化、混合区、抑制和扰乱[11]。其中，泛化是将原始轨迹上的敏感位置替换成一个区域，从而起到保护位置隐私的目的。k−匿名是一种最常用的泛化手段，它将真实位置信息替换成至少包含k个用户的空间区域。文献[12]提出了一种双k机制，通过将k个查询位置发送到不同的匿名器以实现k−匿名。文献[13]在k−匿名的基础上针对敏感的数据集提出了一种改进的K-means 算法。混合区是对轨迹中的某些位置用假名代替，以阻止用户轨迹随着时间变化的可追溯性，使攻击者不能获取用户的真实位置信息。文献[14]提出了一种基于用户流的算法来估计图中节点间的迁移率，并针对迁移率的攻击方法，对传统的混合区进行了改进。抑制是在发布位置时对某些敏感位置进行屏蔽或时延等。文献[15]提出了2 种基于频次的轨迹发布方法，分别通过抑制整个缺陷轨迹和特定的局部抑制实现隐私保护。扰乱即位置扰动，它将各个时间点的真实位置通过替换或添加噪声等方式生成假的位置，以隐藏用户的真实位置，是一种被广泛应用的位置隐私保护机制。文献[16]提出了一种动态假名方案，用于构造移动用户的备用可能路径以保护其位置隐私。文献[17]提出了一种新颖的基于扰动的方案，即使在显示用户身份时也可以保护连续LBS 的查询隐私。

满足差分隐私的位置扰动方法研究逐渐成为轨迹数据隐私保护的热点。差分隐私概念由Dwork等[18-19]于2006 年提出，通过添加少量高斯或指数分布的随机噪声来扰动数据库查询的真实答案，从而保护隐私。其主要思想是降低数据集中添加或删除某一条数据对查询结果的影响，从而让攻击者很难通过多次查询推理数据集中的某条真实数据，即假设攻击者能够获得除目标记录外所有其他记录的最大背景知识。在此假设下，差分隐私对基于各种背景知识的攻击具有很好的保护效果，因为这些背景知识不可能提供比最大背景知识更丰富的信息。差分隐私可大致分为以下2 类[19-22]：中心化差分隐私和本地化差分隐私。中心化差分隐私将原始数据集中到一个数据中心，然后发布满足差分隐私的相关统计信息，因此中心化差分隐私对敏感信息的保护始终基于一个前提，即可信的第三方数据收集者，保证第三方数据收集者不会窃取或泄露用户的敏感信息。但是，在实际应用中，无法找到绝对安全的第三方数据收集者。本地化差分隐私是将数据的隐私化处理过程转移到每个用户上，使用户能够单独地处理和保护个人敏感信息。基于本地化差分隐私的轨迹数据隐私保护大致可以分为2 个方面：历史数据的发布[23-28]和实时位置数据的发布[29-30]。实时位置数据的发布机制因其可以应用于各种基于位置服务的商业软件，从而有较高的应用价值和研究价值。

文献[29]基于差分隐私的Geo-Indistinguishability机制，提出一种可以使隐私级别适应于多种区域的方法。文献[31]将差分隐私保护的发布机制利用线性规划技术进行优化，提出了一种满足地理不可分辨性的δ-spanner 解决方案。文献[30]利用马尔可夫链表示轨迹上各个位置点的时序关系，重新定义了相邻数据集这个概念，提出一种基于敏感度外壳的差分隐私位置发布机制。文献[32]为了解决当前发布位置对以前真实位置的影响，提出了一种基于时空相关性的差分隐私轨迹保护机制。文献[33]通过对轨迹上敏感位置点及其附属敏感点的保护，并结合用户轨迹位置的敏感度和用户隐私保护的要求和隐私预算，提出了一种基于互相约束的个性化差分隐私保护方法。文献[34]设计了一种基于雾计算和k−匿名的轨迹保护方案，用于连续查询中的实时轨迹隐私保护和轨迹发布中的离线轨迹数据保护。

然而，现有的实时差分隐私位置发布机制大部分仅保证了轨迹的隐私性，并没有针对不同敏感度的位置分配不同的隐私预算，且没有考虑发布位置形成的轨迹形状，造成轨迹可用性变差。

3 预备知识

表1 总结了本文的常用符号。

3.1 发布位置定义

为了获得状态概率转移矩阵，需要将轨迹GPS坐标转换为不同时刻的状态，而将GPS 坐标转换为状态，需要先形成坐标系。将地理形状按照同比例形式放入直角坐标系，并将轨迹的经/纬度位置坐标转化为直角坐标系内坐标。将地图划分成网格后，通过统计历史轨迹数据可以得到概率转移矩阵。根据文献[30,32]中的网格划分方法，本文将网格设置为长宽均为0.34 km 的正方形，网格中的位置的编号格式如图2 所示。整个坐标系的编号规则为：从左到右依次递增，从下到上依次递增。

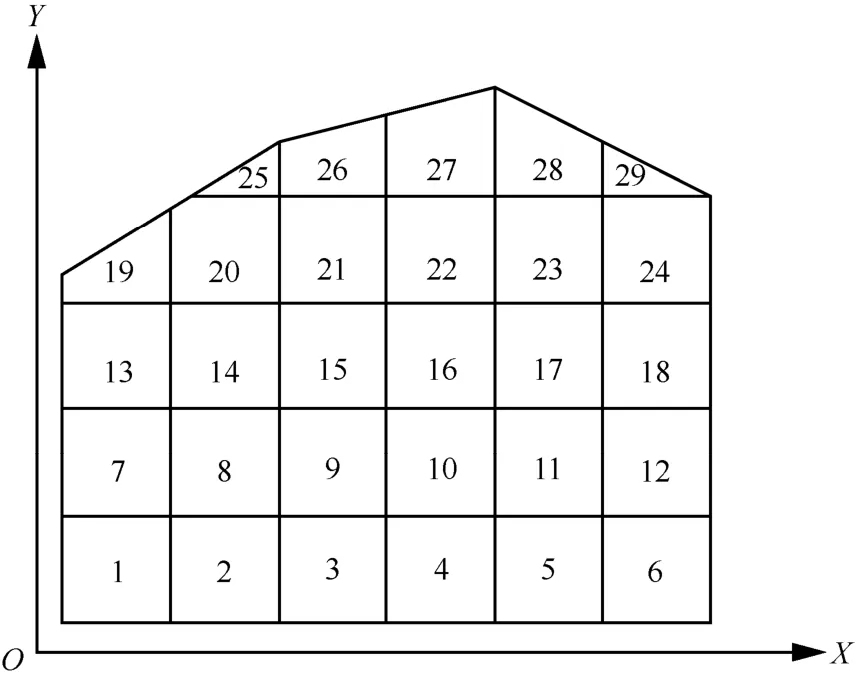
图2 位置发布时的地图定义

3.2 差分隐私

差分隐私是对原始数据或原始数据查询结果添加随机噪声，使最终结果与真实结果尽可能相像，且最大限度地减少识别其记录的机会。差分隐私中使用了相邻数据集的概念：如果结构相同的2 个数据集D和D'有且仅有一条数据不同，那么这2 个数据集被称为相邻数据集。下面，给出差分隐私的形式化定义。

定义1差分隐私[18-19]。给定相邻数据集D和D'及在D和D'上的一个算法A，若算法A在D和D'上的任意输出结果O满足式(1)，则说明算法A满足差分隐私。

其中，参数εt是t时刻的差分隐私预算，表示t时刻的隐私保护程度。εt越大，说明t时刻的隐私保护程度越低；当εt趋近于0 时，则说明t时刻算法A在相邻数据集D和D′上输出结果相差不多，此时算法A不会泄露数据集中任何数据的敏感信息。

然而，轨迹数据中每一时刻的位置信息均可能属于敏感信息，因此轨迹数据隐私中并不存在传统的相邻数据集概念。本文借鉴文献[20-21,30]中对轨迹隐私保护中差分隐私的定义，即已知t时刻的发布位置为ot，根据发布位置，推断当前时刻真实位置的后验概率Pr(tlt|ot)除以当前时刻真实位置的先验概率Pr(tlt)的值满足差分隐私定义，描述为

其中，εt是t时刻真实位置所在区域的差分隐私预算。因此发布位置ot是经过隐私化处理的数据，满足本地化差分隐私的概念，即由用户进行隐私化处理。

若设定的隐私保护预算为ε，实际保护后的隐私保护预算为ε'，若ε＜ε′，则实际的隐私保护强度小于设定的隐私保护强度。

3.3 信息熵及相对熵

信息熵是系统对信息量的期望，信息量是对信息的度量，而信息量与具体发生的事件有关。信息量的大小与随机事件的概率有关，概率越小的事件发生后产生的信息量越大，概率越大的事件发生后产生的信息量越小。信息量定义为

其中，p(x)为事件发生的概率，负号是为了保证信息量大于或等于0。

信息量用于度量一个随机事件发生后所带来的信息，而信息熵则是在结果产生之前对可能产生的信息量的期望，即考虑该随机变量的所有可能取值。信息熵也常用来衡量一个系统的复杂程度，系统越复杂，信息熵越大；反之，一个系统越简单，可能出现的情况种类越少，则信息熵越小。信息熵定义为

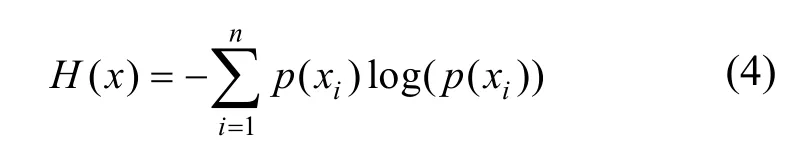
其中，p(xi)为事件发生的概率，与信息量的计算式相同，信息熵计算式中的负号也是为了保证信息熵大于或等于0。与信息熵不同，相对熵是用来衡量2 个概率分布之间的差异，又称为 KL 散度（Kullback-Leibler divergence），定义为

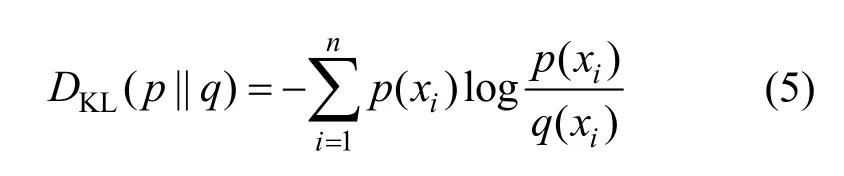
根据式(5)可知，相对熵具有如下性质。

1)如果2 个分布p(xi)和q(xi)相同，那么相对熵等于0。

2)不对称性，即DKL(p||q)≠DKL(q||p)。

3)DKL(p||q)≥0。

根据相对熵的性质可知，只有当p(xi)=q(xi)时，其值为0。若p(xi)和q(xi)略有差异，其值就会大于0，因此相对熵的值越小，则表明2 个概率分布之间的差异越小。

4 轨迹形状相似性与轨迹可用性

为了描述2 条轨迹在视觉上的相似度，本文通过Fréchet 距离来衡量2 条轨迹的形状相似性。Fréchet 距离最早由Fréchet 提出，随后由Alt 等[35]给出了计算方法。如前文所述，大多数位置发布机制没有考虑轨迹形状对于轨迹可用性的影响，因此为了提高轨迹的可用性，本文从轨迹形状相似性方面进行优化，通过计算Fréchet 距离衡量2 条轨迹之间的相似度，Fréchet 距离越小，2 条轨迹之间越相似；反之，2 条轨迹之间越不相似。Fréchet 距离离散化的表示形式为

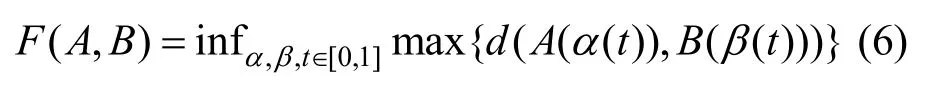
其中，A和B分别为2 条曲线，t为时间点，A(α(t))、B(β(t))分别为曲线上A和B在t时刻的采样点，d(A(α(t)),B(β(t)))为2 个采样点之间的欧氏距离。在每次采样中，t离散地遍历区间[0,1]，得到该种采样下的最大距离max{d(A(α(t)),B(β(t)))}。离散Fréchet距离是连续Fréchet 距离的近似，当曲线选取的离散点足够多时，则近似等于连续Fréchet 距离。

假设某时刻可能的发布位置为ot，真实位置为zt，则本文将这2 个位置之间的距离作为误差评价，可以描述为

如果发布位置与真实位置距离误差为零，则说明2 个位置点重合，即发布位置与真实位置重合；反之则说明发布位置与真实位置不重合。

特别地，对于长度为n的轨迹，同样以距离误差[27,36]为基础定义轨迹可用性，如式(7)所示，距离误差TA 为发布位置与真实位置的均方根误差之和，可以描述为

对某条发布轨迹而言，其距离误差TA 越大，说明其与真实轨迹重合度越低，从而其可用性也就越差。因此，可以通过计算发布轨迹的距离误差来判断轨迹的可用性。

通过计算Fréchet 距离衡量发布轨迹和真实轨迹的形状相似度，通过距离误差计算发布轨迹的可用性，发布轨迹与真实轨迹间的形状相似度越大，距离误差就会越小，则发布轨迹的可用性就会越高。

5 σ−隐私模型

对于差分隐私位置扰乱算法，为不同位置分配相同的隐私预算并不合理，一方面会造成隐私预算的浪费，另一方面会造成位置节点的可用性变差。根据差分隐私的定义，隐私预算越少，保护强度越大，因此应为敏感位置分配较少的隐私预算，为不敏感位置分配较多的隐私预算。根据不同位置点与理想状态的相对熵得到不同的敏感度，而不同的敏感度需要不同的隐私级别，本文提出了一个位置敏感的隐私级别实时计算算法，并将其与隐私预算结合，建立σ−隐私模型。

5.1 发布位置集合

通过对数据集中历史轨迹进行统计，并根据前文提到的发布位置定义，将GPS 数据与地图中预设的格子对应起来，得到状态转移矩阵。由于一个系统的某些因素在转移中的第n次结果只受第n−1 次的结果影响，即只与当前所处状态有关，而与过去状态无关。因此可以根据状态转移矩阵，在当前时刻推测下一时刻可能位置的集合PRN，并对PRN 进行扩充，扩充规则为：以PRN 中的点形成凸包，求出凸包的中心点，以该中心点为圆心，通过控制半径的大小来扩充整个集合，判断某一点是否属于可能发布位置的集合中。判断规则为

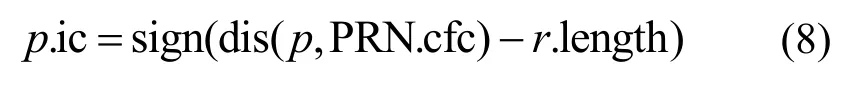
其中，p表示要判断的点，PRN.cfc 表示集合PRN的凸包的中心点，dis(a,b)表示a 点与b 点间的距离，r.length 表示圆的半径，p.ic 表示判断结果，只有p.ic=−1 时，该点才为集合中的点。扩充规则可以简化为：以集合PRN 的凸包的中心点为圆心，选定一个值为半径，圆内的点的并集。半径的值越大，集合越大。扩充后的集合为PRNN={pr1,…,prm}。

扩充规则具体如图3 所示。

图3 中灰色的区域为可能发布的位置区域，如上述规则所示，如果发布位置的中心与圆心距离大于圆的半径，则该位置不能被扩充到集合中。图3中，位置a 的中心与圆心的距离大于圆的半径，则位置a 不属于可发布位置集合中，虚线为圆心到位置的距离，加粗的线为圆的半径。

图3 扩充规则

5.2 隐私级别计算

如果历史数据被敌手获得，敌手可以推测出状态转移矩阵，进而可以根据状态转移矩阵得到下一时刻可能存在位置的集合PRN，并根据PRN 大概率得到下一时刻的位置节点，因此本文采用信息熵来衡量敌手获得可能存在位置集合后能获得多少信息，并根据敌手获得的信息量设定不同的敏感度。首先设定一个理想状态，在该状态下即使被敌手获得可能存在位置集合，也无法大概率得到下一时刻的位置节点。

理想状态具体解释如下。假设有2 个路口R 和S，路口R 和S 分别有2 条岔路，其中旅行者在路口R去往每条岔路的概率为(1/2,1/2)，在路口S 去往每条岔路的概率为(1/4,3/4)，由于信息熵是对“不确定现象”的数学化度量，旅行者在路口S 与在路口R 相比，显然在路口R 的选择更加不确定，而在路口S则大概率会去往第二条岔路，因此，如果去往各个岔路的概率是平均分布的概率分布，则岔路口的去向具有更大的不确定性。因此本文中提到的理想状态是一个大小与集合PRNN 相同，且每一个位置点的概率都为1/m的位置点的集合，因为这种理想状态具有比PRNN 的概率分布更大的不确定性。

本文采用相对熵描述集合PRNN与理想状态的概率分布差异，并以相对熵与理想状态的信息熵的比值作为真实位置点的敏感度，可以描述为

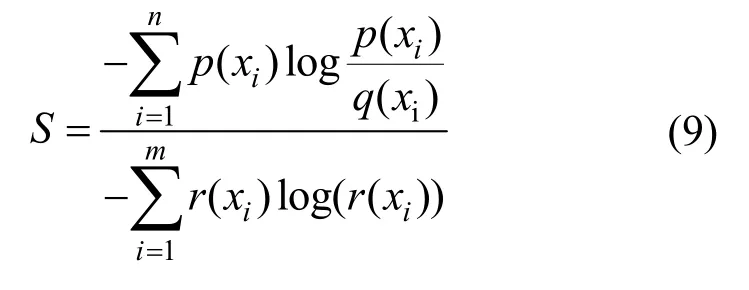
其中，r(xi)为理想状态中某一个事件的概率，p(xi)为PRNN 中某一个事件的概率，q(xi)为PRNN 中的某一个事件在理想状态中对应事件的概率。式(9)中分母为理想事件概率分布的信息熵；分子为相对熵，对应理想事件与实际事件概率分布的信息熵的差值。因此，敏感度S表示实际事件距离理想事件所需信息熵占理想事件信息熵的比值。

根据敏感度确定PRNN 中各个点的隐私级别，规则如下。确定PRNN 中的点k是否属于PRN，如果k点不属于PRN，则k点的隐私级别为s/m；如果k点属于PRN，则该点的隐私级别为(1−S)k.pr，k.pr 为k点对应状态转移矩阵中的值。上述规则可以总结为，对于属于PRN 的点，分配较高的隐私级别；对于不属于PRN 的点，分配较低的隐私级别。因为PRN 中的点是下一时刻大概率会出现的位置，所以对于大概率出现的位置应分配更高的隐私等级，对于下一时刻小概率出现的位置，应分配更低的隐私等级。

位置敏感的隐私级别实时计算算法如算法1所示。

5.3 建立差分隐私模型

在本地差分隐私预算基础上，结合位置敏感的隐私级别实时计算算法，本文提出了σ−隐私模型。

定义2位置σ−隐私。如果一个发布位置能够满足σ−隐私，则该点的差分隐私预算ε和隐私级别pl 满足

由式(10)可知，在σ相同的情况下，隐私级别pl 越大，则为该位置分配的隐私预算ε越小。根据差分隐私的原理可知，一个位置的隐私级别越大，其保护强度就会越大；反之，保护强度越小。当pl=1 时，ε=σ。由于本文算法是实时分配可能发布位置的隐私级别，发布位置之前要计算可能发布位置集合中各个位置的隐私级别，因此隐私模型不能太复杂，以免使算法的时间复杂度过高。

6 基于K-means 的形状相似差分隐私轨迹保护机制

为了解决连续轨迹隐私保护机制轨迹可用性较差的问题，本文提出了一种基于K-means 的形状相似差分隐私轨迹保护机制。该机制首先要保证轨迹中每个发布位置的隐私性，其次通过K-means 算法使发布轨迹的方向与真实轨迹相似，优化轨迹形状相似性，提高轨迹的可用性。

6.1 隐私预算

根据轨迹数据中差分隐私的定义，隐私预算是发布位置的后验概率与先验概率的比值，而发布位置的先验概率和后验概率都需要通过马尔可夫概率转移矩阵得到。下面，说明如何获得马尔可夫概率转移矩阵。

本文使用一阶马尔可夫链模拟用户真实位置之间的相关性，并通过统计用户的历史记录得到状态转移矩阵M。M是一个二维矩阵，矩阵中的元素mij表示用户从第i个区域转移到第j个区域的概率。

假设用户真实位置区域集合为TL={tl1,…,tlt}，利用差分隐私位置发布机制处理后，生成的扰乱区域集合为DL={dl1,…,dlt}。利用马尔可夫状态转移概率矩阵M，结合本文提出的位置敏感的差分隐私位置发布机制，对t时刻存在的位置进行推测，并构建t时刻的真实位置可能发布的集合PL={pl1t,和每个位置的先验概率值的集合其中，n为集合中元素的个数。当t时刻的扰乱位置dlt发布后，就可以根据此扰乱位置推测出t时刻的真实位置tlt，即发布位置的后验概率Pr(tlt|dlt)，并将各个时刻的后验概率形成集合为计算后验概率，考虑如何求得t时刻的差分隐私位置发布概率矩阵Rt。设t时刻发布的位置区域集合为PRNN={pr1,…,prm}。矩阵Rt是一个维度为n×m的矩阵，元素为t时刻真实区域到发布的扰乱区域为的概率值。则位置的后验概率为

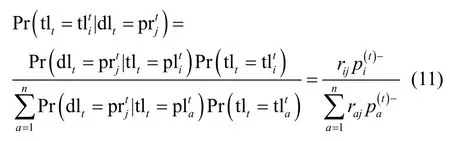
通过式(11)，可以得到每个区域位置的后验概率，进而得到每个位置的隐私预算，并判断该区域的隐私预算是否小于预设的预算。本文将各个区域的隐私预算形成一个隐私预算集合ept={ep1t,…,epmt}。

6.2 位置发布算法描述

为了使发布轨迹与真实轨迹方向尽可能一致，首先利用K-means 算法，对PRNN 中的位置点进行聚类，选择与真实轨迹方向最相近的簇为备选集合；然后对备选集合内的位置点根据式(6)计算t时刻与t−1 时刻真实位置的轨迹与发布位置的轨迹的Fréchet 距 离，并 形 成 Fréchet 距 离 集 合frt={fr1t,…,frmt}；最后选择符合隐私预算且Fréchet距离最小的位置点作为发布位置点。位置发布算法如算法2 所示。

算法2位置发布算法

输入真实位置的转移概率矩阵M，轨迹的隐私保护预算ε={ε1,…,εt}，圆的半径r，t−1 时刻的真实位置tlt−1，t时刻的真实位置tlt，t−1 时刻的干扰位置dlt−1

6.3 算法分析

位置发布算法的运算时间是对集合PRN 扩展的时间、对集合PRNN 聚簇的时间以及运算Fréchet距离的时间之和。其中，对PRN 扩展的时间与理想状态的大小有关，对PRNN 聚簇的时间与簇头个数有关，运算Fréchet 距离的时间与簇内位置的个数有关。

在隐私和可用性方面，由于采用了满足差分隐私的保护机制，并且引入了相对熵和K-means 算法，既可以使t时刻的发布位置满足εt差分隐私，又能使发布轨迹与真实轨迹尽可能相似。因此，在保证隐私的前提下，算法选择使发布轨迹与真实轨迹方向相似，且使轨迹形状也相似的位置点作为发布位置，在满足轨迹隐私性的前提下，通过轨迹形状相似性提高了轨迹的可用性。

7 实验与分析

本文采用数据集Geolife 和Gowalla 对DPKTS进行实验分析。Geolife 数据集包含182 个用户于2007 年4 月到2012 年8 月在北京活动的真实数据，一共有1 7621条轨迹。Gowalla数据集包含了15 116个用户于2009 年2 月到2010 年10 月在加州范围内移动社交网站上签到的数据，共6 442 890 个签到位置。对上述2 个数据集，抽取用户编号、时间戳、经度和纬度作为新的数据集。

实验的环境如下：Intel i7-9700K 3.6 GHz，16.00 GB 内存，Microsoft Windows 10 操作系统，算法均在Pycharm2018 下实现。

对于DPKTS，本文主要分析隐私模型参数σ及簇头个数对轨迹可用性的影响、理想状态的大小对运算时间的影响，以及簇头个数对运算时间的影响。在衡量σ对轨迹用性的影响时，本文将DPKTS 与PIM（planar isotropic mechanism）[30]和DPLRM（differentially private location release mechanism）[32]进行对比。这2 种对比方法都是基于差分隐私的实时轨迹保护方法，且DPLRM 考虑了时序相关性。

首先，针对σ对发布轨迹可用性的影响进行实验分析。在DPKTS 中，σ与传统差分隐私中的隐私保护预算ε等价。如图4 所示，DPKTS 的可用性较好，因为DPKTS 对位置是敏感的，而不同位置的敏感度不同，所以针对不同位置设定不同隐私级别且通过K-means 算法得到与真实轨迹方向最相似的备选集合，并以轨迹形状相似性为优化目标，从而提高了轨迹的可用性，所以DPKTS 的轨迹可用性明显优于其他方法。PIM 并没有考虑轨迹的可用性，仅对发布位置做了基于差分隐私的处理，所以轨迹可用性一般。DPLRM 的轨迹可用性较PIM 略好，这是因为DPLRM 在满足差分隐私的同时，还对轨迹中的半马尔可夫模型进行优化。但由于DPLRM没有针对轨迹可用性进行优化，轨迹可用性比DPKTS 略差。不同方法在Geolife 数据集上的表现均优于在 Gowalla 数据集的表现，这是因为Geolife 数据集采样频率更高，细粒度更好，所以结果更精确。

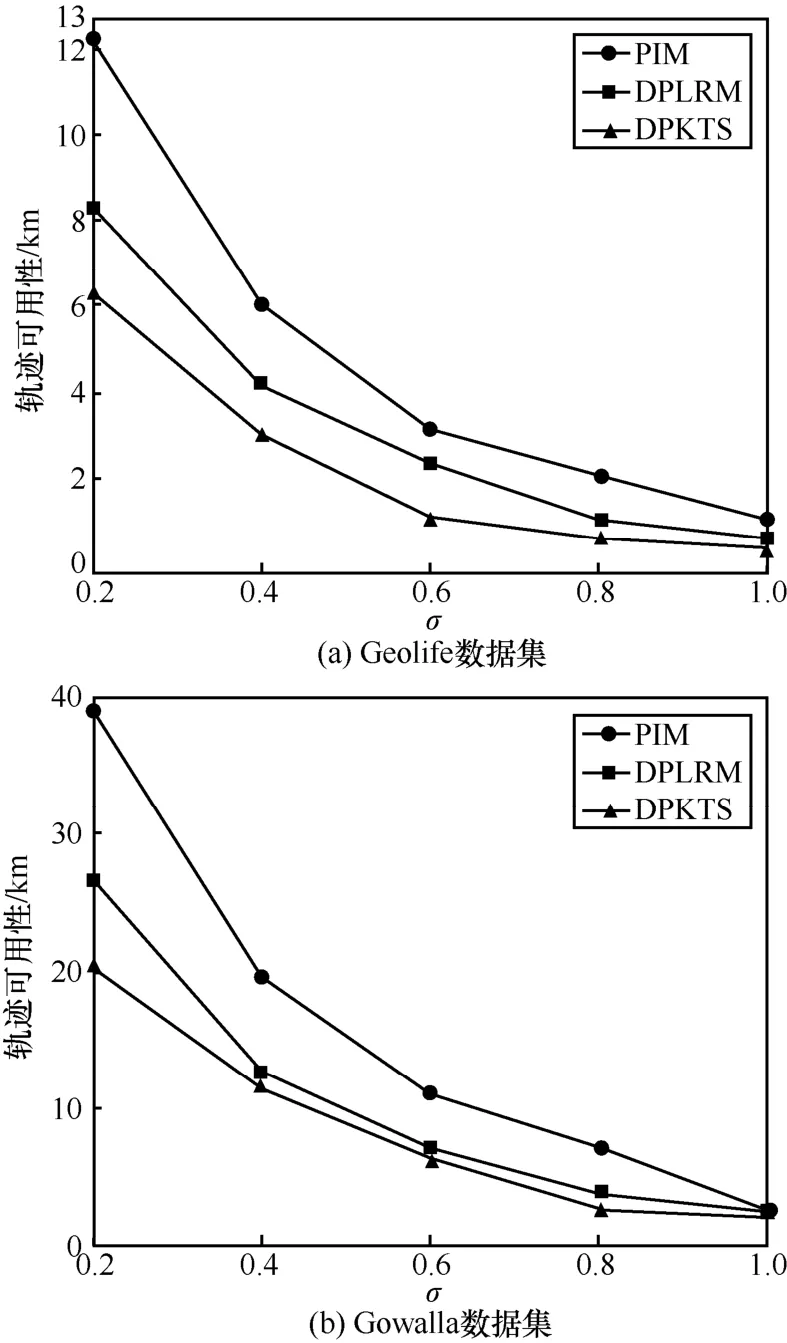
图4 σ 对轨迹可用性的影响

本文还分析了簇头个数对轨迹可用性的影响，当理想状态数目为121、σ为1 时，分别计算不同簇头数对于方法可用性的影响结果，如图5 所示。随着簇头数的增加，轨迹可用性逐渐变差。这是因为随着簇头数的增加，每个簇中可选择的位置点变少，且DPKTS 选择与真实轨迹方向最相似的簇，所以当簇头数增加时，簇内位置点变少，轨迹可用性降低。

图5 簇头数对轨迹可用性的影响

图6 展示了不同数据集上隐私保护强度的对比结果，其中横坐标为设定的隐私保护强度，纵坐标为实际隐私保护强度，ε′值越小，说明保护强度越好。从图6(a)可以看出，DPKTS 的隐私保护强度与PIM 的隐私保护强度接近，最坏的情况是在σ=0.4 时，此时也只比PIM 降低了约2.6%，这是因为DPKTS 旨在提高轨迹可用性，而PIM旨在提高轨迹的保护强度，忽略了轨迹的可用性。与同样旨在提高轨迹可用性的 DPLRM 相比，DPKTS 具有更好的隐私保护强度。当σ=0.6 时，DPKTS 比DPLRM 的隐私保护强度提高了2.0%。在图6(b)中，由于所使用的数据集时序相关性较弱，采样率较低，使不同方法的隐私保护强度更接近，可以看出DPKTS 对时序相关更强的数据有更好的表现。

其次，分析理想状态的大小对运算时间的影响，实验中聚类时的簇头数为3，结果如图7 所示。从图7 中可以看出，运算时间与理想状态的数目成正比，即理想状态数目越多，运算时间越多。这是因为理想状态数目越多，计算位置点的敏感度所需要的时间越多，计算各个位置点的隐私级别所需要的时间越多，在聚类后，簇中节点数也会增加，所以理想状态数目越多，运算时间越长。

图6 隐私保护强度

图7 理想状态数目对运算时间的影响

最后，分析簇头数对运算时间的影响，结果如图8 所示。实验中，分别以不同理想状态大小进行实验，并对不同理想状态数目设定多组实验，以不同簇头数进行实验。由图8 可知，当理想状态数目为121、簇头数为1 时，运算时间最少；当理想状态数目为441、簇头数为2 时，运算时间最少。每一种理想状态下，都有可以使运算时间最少的簇头数，因此设定不同理想状态数目时，需要选用不同的簇头数，不能使用相同簇头数。但是，当理想状态数目逐渐变多时，簇头数也应逐渐变多，才可使预算时间最小。

图8 簇头数对运算时间的影响

8 结束语

针对位置服务中轨迹隐私保护问题，本文通过实时计算真实位置的相对熵衡量其敏感度，并根据敏感度为可能发布位置分配不同的隐私级别；通过结合节点隐私级别与差分隐私预算建立σ−隐私模型；利用K-means 获得与真实轨迹方向一致的位置备选集合，使用Fréchet 距离来计算不同轨迹之间的相似程度，实现了一种基于形状相似的K-means 差分隐私轨迹保护机制。实验结果表明，本文方法在保证轨迹隐私性的前提下，提高了轨迹的可用性。