利用互无偏测量构造的可分判据
2021-03-09赵慧,张琳
赵 慧,张 琳
(北京工业大学理学部,北京 100124)
量子信息是一门涉及数学、物理、计算机的交叉学科,包括量子通讯、量子计算、量子编码等很多方向. 它是以量子态的叠加原理为基础,研究信息处理的一门新兴学科. 量子纠缠态理论是量子信息与量子计算领域的一个重要研究内容. 利用纠缠理论可以实现很多经典物理无法解决的问题,例如量子态层析成像[1-2]、量子密钥分配[3]、量子隐形传态和量子超密码编码[4-5]. 因此,判断态纠缠即非可分是一个至关重要的问题. 对于一般态,文献[6]利用密度矩阵的Bloch表示,给出了两体态可分的必要条件和充分条件. 文献[7-8]通过分析对应图的可分性来判断态的可分性. 文献[9-10]利用互无偏测量给出了两体态的可分判据. 文献[11]分析了三体量子态的纠缠性质. 文献[12]进一步给出了多体系统态的可分判据. 文献[13]利用互无偏测量和范数,通过构造矩阵进一步优化可分判据. 对于对角对称态,文献[14]基于部分转置正判据[15],给出了态可分的充要条件. 还有很多文献通过不同的方式给出了不同的可分判据[16-21].
本文利用对角对称态可分时的部分转置正条件,结合对角对称态性质,利用互无偏测量,给出了对角对称态可分的充要条件,又利用密度矩阵的Bloch表示,将密度矩阵和互无偏测量相结合,以及矩阵和向量范数之间的关系,给出了两体量子态可分的必要条件.
1 基础知识
定义1量子系统的态为|φi〉,则称{pi,|φi〉}是态的系综. 式中:i为指标;pi为对应的概率. 系统的密度矩阵定义为

若ρ=|φ〉〈φ|,tr(ρ2)=1,则称ρ是纯态,若tr(ρ2)<1,则称ρ是混态.
定义2一个矩阵ρ是和某个系综{pi,|φi〉}相关联的密度矩阵,当且仅当满足以下条件:
1)ρ的迹等于1;
2)ρ是一个半正定矩阵.
定义3两体Hilbert空间上,若密度矩阵ρ能写成
(1)
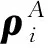
定义4两体Hilbert空间Cd⊗Cd上的态ρ称为对角对称态,当且仅当ρ可以写成
(2)

则称2个基B1和B2是互无偏的.
定义6Cd上的一个标准正交基集合{B1,B2,…,Bm},如果集合中的每一对基都是互无偏的,称为一个互无偏基集合.
定义7Hilbert空间Cd上的2个测量
称为互无偏测量,当且仅当
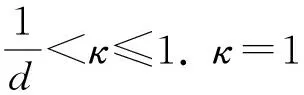
下面给出在d维Hilbert空间上构造d+1个完备互无偏测量的方法.[22]
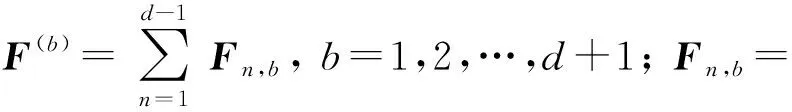
利用以上算子,可以进一步构造d+1个互无偏测量
(3)
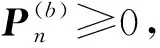
考虑M个含参数κ的互无偏测量集合P={P(1),P(2),…,P(M)},则有不等式
当M=d+1时,称互无偏测量集合P={P(1),P(2),…,P(M)}是完备的,并且
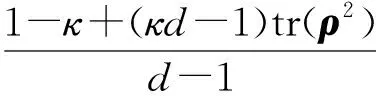
当ρ为纯态时,由于tr(ρ2)=1,此时有
(4)
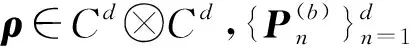
如果ρ可分,则J(ρ)≤1+κ.[9]
定义8将ρ的矩阵元用直积的形式表示为
ρmnuv=〈em|〈fn|ρ|eu〉|fv〉,m,n,u,v=1,2,…
式中:{|eu〉}为第1个Hilbert空间的一组基;{|fn〉}为第2个Hilbert空间的一组基. 则ρ关于第一个子系统的部分转置为
ρ关于第二个子系统的部分转置为
2 对角对称态的可分判据
首先,考虑C2⊗C2上一类对角对称态ρ2×2可分的充要条件. 定义
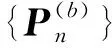
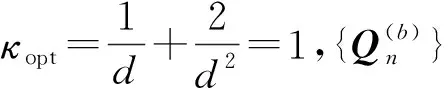
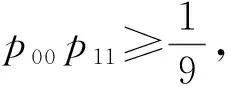
证明:必要性.
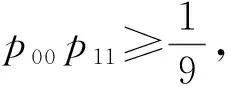
充分性.
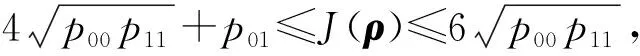
下面考虑C3⊗C3上一类对角对称态可分的充要条件.同样定义
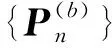
定理2ρ3×3是C3⊗C3上的对角对称态,且元素满足以下条件,
令J(ρ)=J1(ρ)+J2(ρ)+J3(ρ),其中,
(8)
(9)
(10)
式中:
则ρ3×3可分,当且仅当
(11)
(12)
(13)
证明:因为ρ是对角对称态,由文献[14]定理3.3,ρ∈Cd⊗Cd是对角对称态,d≤4,则ρ可分当且仅当ρ是部分转置正的,即
(14)
(15)
(16)
(17)
必要性.

则式(11)得证. 同理可得,式(12)(13)成立.
充分性.
由式(11)得

同理可得,式(15)(16)成立.
由pij≥0及式(6)(7)(14),经化简可得
将三式相加可得
综上可得ρ是部分转置正的,从而ρ是可分的.
3 一般量子态的可分判据
定义9设矩阵A∈Cm×n,q=min{m,n},A*A的q个非负特征值的算术平方根叫作矩阵A的奇异值.
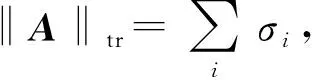
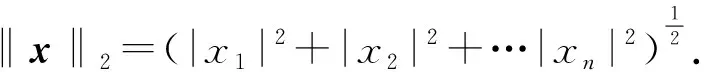
定义12密度矩阵ρ∈Cd可以用单位矩阵Id和SU(d)的生成元λi,i=1,2,…,d2-1来表示

这种表示方法称为密度矩阵的Bloch表示.
定义13设|α1〉和|α2〉是空间A中的任意2个态,|β1〉和|β2〉是空间B中的任意2个态,定义空间B上的偏迹为
trB(|α1〉〈α2|⊗|β1〉〈β2|)=
|α1〉〈α2|tr(|β1〉〈β2|)
空间A上的偏迹为
trA(|α1〉〈α2|⊗|β1〉〈β2|)=
|β1〉〈β2|tr(|α1〉〈α2|)
定义14空间A⊗B上的密度矩阵ρAB,则关于空间A的约化密度矩阵定义为ρA=trB(ρAB),式中:trB是空间B上的偏迹.
定义15N阶特殊酉群是指行列式值为1的N×N阶酉矩阵组成的群,记为SU(N).

当i=1,2,…,N-1时,
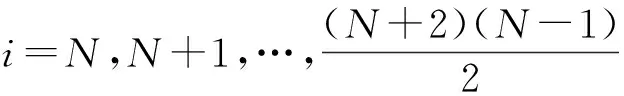
λi=|j〉〈k|+|k〉〈j|
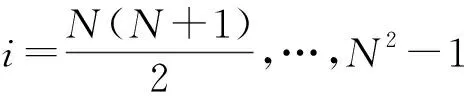
λi=-i(|j〉〈k|-|k〉〈j|)
定义17密度矩阵ρ∈Cd1⊗Cd2的Bloch表示为
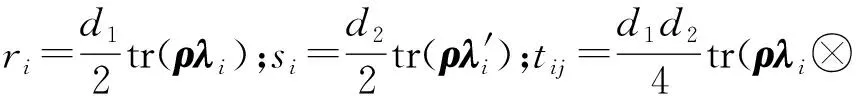
密度矩阵ρAB关于空间A和B的约化密度矩阵分别为
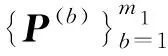
(18)

定义
M(X,Y)(ρ)=(mij)6×6∈C6×6
(19)
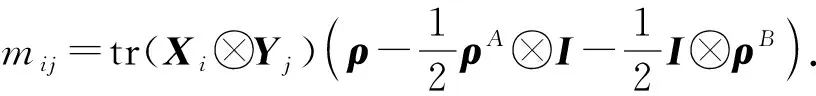
则有下面的定理3.
定理3ρ是C2⊗C2上的密度矩阵,如果ρ可分,则‖M(X,Y)(ρ)‖tr≤2.
证明:由定义13,式(18)(19)可得
M(X,Y)(ρ)=

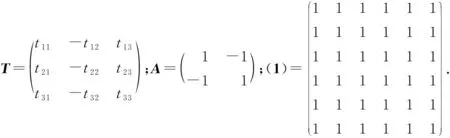

例1 已知两体量子系统C2⊗C2中态为
ρ=p|φ±〉〈φ±|+(1-p)|00〉〈00|
(20)
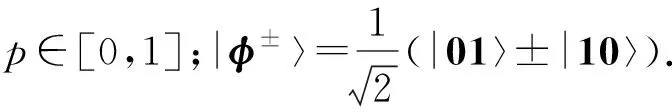
文献[9]的方法无法检测出p取何值时态纠缠. 但由定理3可得,当0.5 下面考虑ρ∈Cd1⊗Cd2时的可分性. 利用式(18),定义 则有下面的定理4. 定理4ρ是Cd1⊗Cd2上的密度矩阵,如果ρ可分,则 证明:若ρ纯态可分,则ρ=|φ〉〈φ|⊗|η〉〈η|,M(X,Y)(ρ)=(tr(Xi⊗Yj)ρ)d1m1×d2m2=(tr(Xi|φ〉〈φ|)tr(Yj|η〉〈η|))d1m1×d2m2=βηT 式中: 则 ‖M(X,Y)(ρ)‖tr=‖βηT‖tr=‖β‖2‖η‖2= 例2 已知两体量子系统C2⊗C2中态为 ρ=p|φ〉〈φ|+(1-p)ρsep (21) 由定理4可知,当0.267 7 本文研究了密度矩阵的可分条件,给出了对角对称态可分的充要条件和两体量子态可分的必要条件. 1) 利用对角对称态可分和部分转置正的关系,研究了C2⊗C2空间上的一类对角对称态,给出了态可分的充要条件. 2) 研究了C3⊗C3上满足一定条件的对角对称态的可分性,结合对角对称态的性质,给出了态可分的充要条件. 3) 对C2⊗C2上的量子态,将密度矩阵进行Bloch表示,根据互无偏测量和SU(2)生成元之间的关系,给出了量子态可分的必要条件,并用例子说明了本文的可分判据能够检测出更多的量子纠缠态. 4) 对Cd1⊗Cd2上的量子态,利用迹范数与向量范数之间的关系以及互无偏测量和密度矩阵之间的关系,给出了量子态可分的必要条件,并用例子说明用此判据可以检测出更多的纠缠态.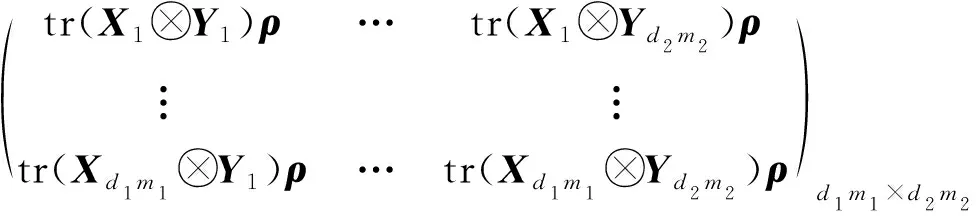

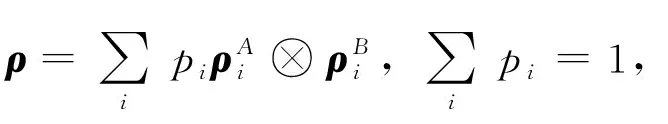

4 结论
