气管插管蛇形机器人关节运动分析与解耦方法研究
2021-03-09许德章汪步云
杨 龙,许德章,汪步云
(安徽工程大学 人工智能学院,安徽 芜湖 241000)
气管插管术是将一特制的气管内导管通过口腔或鼻腔,经声门置入气管或支气管内的方法,为呼吸道通畅、通气供氧、呼吸道吸引等提供最佳条件,是抢救呼吸功能障碍患者的重要措施。气管插管操作技术复杂,需要技艺精湛的医务人员才能胜任。针对新冠肺炎等高度传染病患者,在插管操作的过程中,医务人员面临着很高的职业暴露和传染的风险。利用机器人完成气管插管操作,对于降低医务人员的工作强度,避免感染风险,无疑具有非常重要的意义。早在2010年,Tighe等利用达芬奇机器人系统,完成了两例模拟人体气管插管手术,开创了机器人气管插管的先例;T.M.Hemmerling等研制出开普勒机器人(KIS),利用模拟人和动物开展了可行性实验研究,并取得了初步成功;在国内,海军军医大学王新宇研制的遥操作气管插管机器人系统,以成年猪为实验对象完成了验证实验,但尚未开展人体实验。上述实验研究虽都取得一定的经验,但由于实验器械属于刚性连接,弯曲变形能力差,极易损伤上呼吸道,存在重大安全隐患。
蛇形机器人属于超冗余连续型串联机构,是仿生设计学和机器人技术相结合的产物,其不仅具有软体动物弯曲半径小、柔性高、动作灵活等特点;又因关节采用刚性部件,易维持自身结构,具有较高的鲁棒性;此外,将蛇形机器人的工作臂段与驱控部件完全分离,使其对非结构化环境具有较强的适应性,多用于非自由空间的作业任务。目前,各国研究人员对绳驱蛇形机器人进行了一定的研究。英国OC公司率先实现了绳索柔性机器人的商业化,应用于飞机油箱检修、核电站勘察以及狭小空间焊接作业等领域。哈尔滨工业大学对绳索柔性机器人的研究一直领先于其他高校,研发出面向不同工况的机器人,包括单孔腔镜手术的连续型机器人、腹腔镜微创手术机器人系统、狭小空间作业的绳驱超冗余机械臂等其他优秀产品。鉴于蛇形机器人有着良好的弯曲特性以及对非自由化环境有着极强的适应能力,非常适合气管插管术操作,因此,把蛇形机器人作为运动载体,引导气管进入呼吸道可以完成气管插管作业。
对于具有n
个自由度的绳驱柔性机器人而言,卡拉特欧多定理表明,最少需要n
+1条具有正张力的驱动绳索才可实现约束,而斯坦尼茨定理表明,最多需要2n
条具有正张力的驱动绳索。对于单关节具有俯仰和偏航两个自由度的蛇形机器人来说,至少需要3根驱动绳索才能实现完全约束。蛇形机器人多由3~5个关节甚至十几个关节模块串联而成,那么必将引入关节3倍数量的驱动绳索进行约束,而驱动绳索往往由电机实施控制,如此大数量的电机如何协同高效地工作,将给机器人的控制带来极大挑战。且后一关节的驱动绳索由前一关节引出,当驱动绳索调整关节姿态时,近端关节必将与远端关节相互干扰,构成复杂的耦合关系。基于绳索驱动蛇形机器人有着上述问题,因此提出一种基于关节联动的主被动混合蛇形机器人连接方案。通过配置合理的联动关节构型,采用远近端关节联动方法,使关节间产生联动。而后对其建立运动学模型,针对蛇形机器人关节之间存在复杂耦合问题,对单关节的驱动空间、关节空间以及操作空间之间的映射关系进行数学分析,实现气管插管机器人的运动解耦。
1 蛇形机器人构型设计
1.1 任务需求分析

图1 建立人工气道示意图
气管插管术即为建立人工气道的过程,示意图如图1所示。由图1可知,在喉镜辅助下,将一特制的气管内导管依次通过口、悬雍垂、会厌、声门裂几个重要的解剖学标志位,直达气管或支气管内的方法。整个操作过程都在复杂且敏感的上呼吸道环境内完成,因此在设计气管插管蛇形机器人时,应具备以下特性:优良的弯曲特性和灵活的运动性能;尽可能地减少驱动电机数量,降低控制难度;精简包络尺寸,微小型化设计。
1.2 联动关节理论分析
蛇形机器人单关节是由具有俯仰和偏航两个自由度的十字轴组成,分别对应绕X
轴和Z
轴两个方向上的转动,远近端关节联动示意图如图2所示。由图2可知,采用了近端联动和远端联动两种方式,分别实现相邻关节X
轴和Z
轴方向上的联动,下面分别介绍两种联动方式的基本原理。
图2 远近端关节联动示意图

图3 近端联动原理图
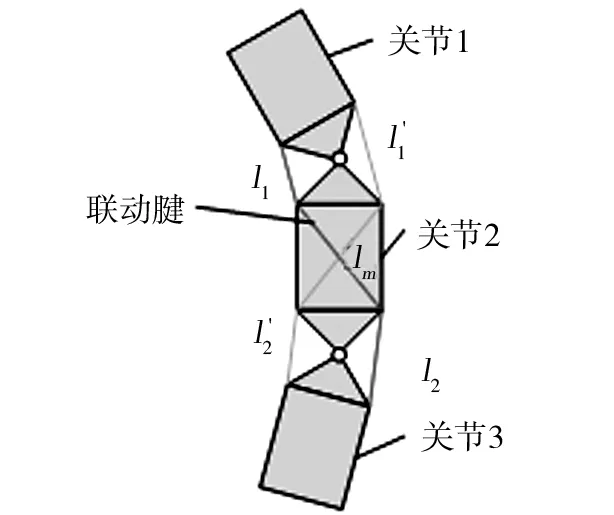
图4 远端联动原理图
(1)近端联动。对于蛇形机器人相邻关节绕X
轴方向上的联动而言,由于在X
轴方向上转动的十字轴都位于同一关节上,其相对位置不会随着关节的运动而改变。近端联动原理如图3所示。由图3可知,在两个十字轴上分别设计了直径相同的定滑轮槽,并使用一对“S
”型绳索连接,便可以实现两个十字轴在绕X
轴方向上的反向等角度耦合,对应图3中θ
=-θ
。
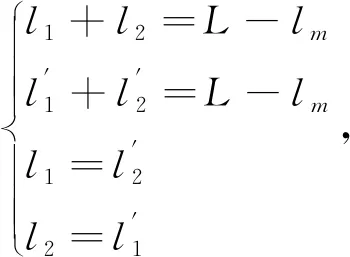
(1)


(2)
也即,联动绳索一侧的伸长量等于另一根联动绳索的缩短量,对应关节角度发生等量反向变化,对应图2中θ
=-θ
,实现关节1和关节3的联动耦合。1.3 联动关节结构设计
蛇形机器人采用主被动混合连接方式,由4个被动关节(联动关节)和1个主动关节(末端执行器关节)串联而成,三维数字模型如图5所示,主要零部件包括十字轴、耳板、法兰盘以及内外套管。由图5可知,关节间采用远近端联动方法进行耦合约束,使原本拥有8个独立自由度的机器人,联动成为仅有两个方向上的自由度,使每个关节在运动角度上保持一致,在机器人外部表现为连续等曲率变化。下面将具体阐述联动方案的实施。

图5 机器人三维装配渲染图
(1)近端联动结构。近端联动结构如图6所示。由图6可知,在一个标准节的两端各自枢接一个十字轴,十字轴的周向上分别设计4个线槽,且同在一个轴线上的滑轮槽槽口方向相同,在槽口的对向设计固定块,以便联动绳索的固定。联动绳索的一端固定于十字轴上,用两颗锁紧螺母紧固,接着联动绳索呈“S”穿过两个对向滑轮槽固定在另一侧十字轴上,与上一侧固定方法不同,联动绳索需穿过中空螺纹杆进行预紧后锁死;另一条联动绳索的连接固定方法相同但方向相反,避免使用同一根绳索发生干涉的可能。两条背对的联动绳索构成完整的近端联动。
(2)远端联动结构。在法兰盘和十字轴中间均设计可供联动绳索穿过的通孔,如图7所示。由图7可知,远端联动绳索的走线与固定方式与上述不同,具体为带有球头的绳索先穿过法兰盘和十字轴上的通孔,然后环绕内侧套管180°后经另一侧的两通孔实施固定,通过中空螺纹杆与法兰盘螺纹配合实现绳索的预紧。其中联动绳索在环绕内侧套管的部分,设计导线软管用于传递绳索、减小摩擦力。另一根联动绳索连接方法相同,但环绕内侧套管的联动绳索从导管的另一侧穿过,这两根穿过一个标准节的联动绳索构成完整的远端联动。

图6 近端联动结构 图7 远端联动结构
2 运动学分析
2.1 蛇形机器人驱动空间与关节空间映射关系及解耦分析
气管插管蛇形机器人由均匀布置在法兰盘圆周方向上的三根柔性绳索驱动。当穿过两个法兰盘间的腱绳长度发生改变时,与法兰盘固定连接关节的角度也会随之发生变化,驱动空间与关节空间的映射关系即为探索驱动绳索长度与关节角度的函数关系。蛇形机器人的单关节弯曲模型如图8所示。忽略驱动绳索与法兰盘穿线孔的间隙,以及驱动绳索穿过线孔处微量曲率的变化,建立了简化模型如图9所示。

图8 关节模型 图9 简化模型
在模型中,法兰盘简化为半径均为R
的平面A
A
A
、B
B
B
;三根驱动绳索简化为直线A
B
、A
B
、A
B
。在两法兰盘间十字轴中心位置建立坐标系{O
},当蛇形机机器人处于初始状态(各个关节相互平行)时,设法兰盘平面到十字轴中心平面的垂直距离为d
,驱动绳索所在法兰盘穿绳孔端面位置与铅垂线的夹角为γ
。当蛇形机器人运动时,其关节角度发生改变,对应模型中平面B
B
B
发生位置变化。将此过程分解为,平面B
B
B
以坐标系{O
}中的Y
轴旋转α
角度,到达坐标系X
Y
Z
;再以坐标系X
Y
Z
中X
轴旋转β
角到达坐标系X
Y
Z
,此时即为机器人运动后的空间姿态。此旋转过程可表达为
(3)
驱动绳索在两法兰盘过线孔的位置矩阵为

(2)
驱动绳长表达矩阵为
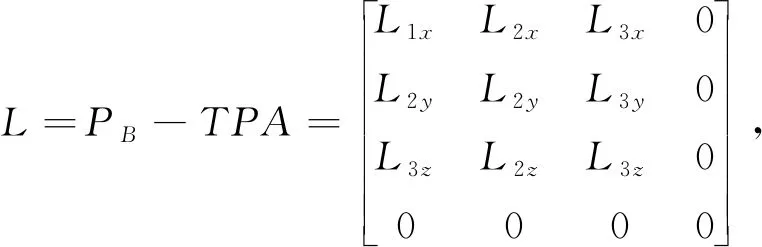
(3)
得到A
B
、A
B
、A
B
长度表达式为A
B
=((d
+dc
c
+Rc
s
+Rc
s
s
)+(ds
+Rs
-Rc
s
)+
A
B
=((d
+dc
c
+23+Rc
s
+Rc
s
+23s
)+(ds
+Rs
-Rc
+23s
)+
A
B
=((d
+dc
c
+43+Rc
s
+Rc
s
+43s
)+(ds
+43+Rs
-Rc
+43s
)+
(4)
前一关节的运动导致后面各臂段绳索长度的变化量可表示为

(5)
式中,i
表示第i
根驱动绳索,函数f
(θ
,θ
,γ
)表示驱动绳索在该角度γ
下,穿过法兰盘绳孔受关节角度θ
θ
影响下的变化量。把这种微小量进行叠加迭代,可得到蛇形机器人各个关节受前面关节的影响量。把求得的驱动绳索长度减去耦合量便可得到实际驱动量,实现了解耦分析。2.2 蛇形机器人关节空间与操作空间映射关系及解耦分析
采用经典D-H参数法,建立D-H坐标系如图10所示,其D-H参数如表1所示。

图10 D-H坐标系

表1 D-H参数表

iai/mmαi/°di/mmθi/°66400θ270900θ286400θ190-900θ
已知,第i
+1参考系相对第i
参考系的齐次变化矩阵如式(6)所示。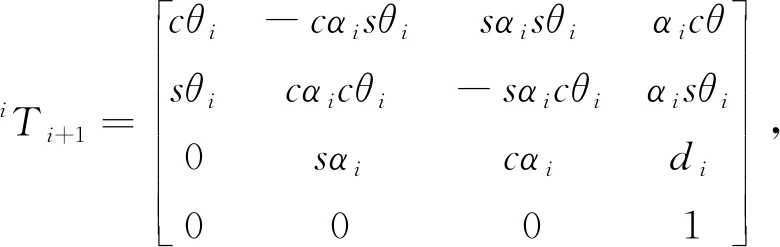
(6)
式中,cθ
=cos
(θ
),sθ
=sin
(θ
),cα
=cos
(α
),sα
=sin
(α
),下文中见此符号含义相同。其末端位姿表达如式(7)所示,其中为简化数学表达式,令a
=2θ
,b
=2θ
。
(7)
把式(7)中各项展开为

(8)

(9)

(10)

(11)
由于气管插管机器人为多个关节耦合联动,单关节有俯仰、偏航两个自由度,在对其进行逆运动学分析时,由上式可分为以下两种情况分析。
(1)当n
=0,则θ
=0,即
(12)
联立解得

(13)
(2)当n
≠0则θ
≠0,即
(14)
联立解得

(15)

(16)
由上述函数表达式易知,当已知蛇形机器人末端位姿时,可用解析法求得关节俯仰和偏航的角度,并且该角度值是唯一确定的,也即关节空间与操作空间存在唯一确定的相互映射关系。
3 仿真分析
3.1 运动学验证
在MATLAB中,运用Fkine和自定义函数分别对正逆运动学进行验证,以θ
=30°、θ
=0°为初始值,在软件中得到机器人位姿、位姿矩阵和关节角如图11所示。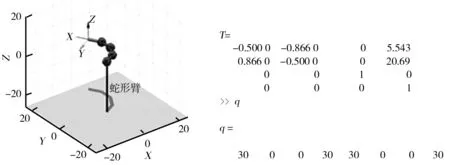
图11 仿真结果
再把初始值带入式(7)、式(16)、式(17)得



不难得出仿真结果与推导计算值相同,验证了模型建立的正确性。
3.2 工作空间求解
根据蒙特卡洛方法,取θ
、θ
在角度变化范围为±30°内的随机值带入,当N
=3 000次可得到蛇形机器人末端工作空间如图12所示。由图12可以看出,工作空间为完整连续的半球面,代表机器人活动范围大,可达域广,满足任务设计需求。
图12 蛇形机器人工作空间
4 结论
研究提出一种基于关节联动的主被动混合蛇形机器人连接方法。通过设计远近端联动构型使蛇形机器人关节间产生联动,实现了减少驱动电机数目、降低控制难度的目的;而后基于所设计的关节构型建立D-H简化模型,推导出气管插管蛇形机器人末端位姿和驱动腱绳长度的解耦映射关系,实现蛇形机器人的运动解耦;最后通过MATLAB仿真验证了运动学分析的正确性,同时也仿真出机器人可达工作空间,满足气管插管术任务需求。
