随机脉冲控制下时变时滞多智能体系统一致性研究
2021-03-09王晨阳吴小太
王晨阳,吴小太
(安徽工程大学 数理与金融学院,安徽 芜湖 241000)
众所周知,多智能体系统在大数据网络分析、无人机编队控制、区块链技术、社交网络以及智能电网等领域都有着广泛的应用。因此在多智能体系统的集群行为研究受到了越来越多的专家学者青睐,特别是在多智能体系统一致性控制研究方面,不同的控制方法被引入多智能体系统的一致性分析中,并获得了丰富的研究成果,如自适应控制、基于事件触发的控制、时间驱动的控制、采样数据控制以及脉冲控制等。
脉冲现象在自然界普遍存在,如人体的脉搏跳动、自然环境的剧变对生物种群的影响、鸟类对行进中飞机的突然撞击等。虽然脉冲发生的时间非常短暂,但却对整个系统运行产生复杂的影响。脉冲控制是一种典型的非连续控制,相对于连续性控制方法具有良好的经济和实用性,因而广泛应用于动态系统控制中,如卫星的燃料优化控制、机器人操纵器的控制等。近年来,脉冲控制在多智能体系统的一致性研究被广泛采用。文献[11]研究了基于脉冲控制、事件触发控制和采样数据控制的两种具有非线性动力学的多智能体系统的一致性问题。文献[12]研究了具有脉冲行为的随机时滞动态多智能体系统的一致性问题。文献[13]提出了一个控制框架,称为脉冲调制间歇性控制,它将脉冲控制和采样控制统一起来研究多智能体系统的一致性。文献[14]研究了有向通信图下的脉冲多智能体系统的一致性问题。
同时,多智能体系统的脉冲控制在工作时会不可避免地受到一些随机因素的干扰,导致脉冲作用的强度发生改变,最终影响了脉冲控制效果。因此,有必要对脉冲控制进行随机刻画。近年来,对于随机脉冲系统稳定性的研究已经取得了一些相关研究成果,然而,对于多智能体系统的随机脉冲控制还需要进一步展开研究,分析脉冲的随机性对多智能体系统一致性控制效果的影响。综上,研究随机脉冲控制下时变时滞多智能体系统的一致性问题,通过引入随机参数来刻画随机脉冲的强度,然后借助Lyapunov函数稳定性的分析方法,得出了随机脉冲控制下时变时滞多智能体一致性的充分条件。
研究的主要贡献体现在以下两个方面:
(1)通过引入随机参数,有效地刻画了一类随机脉冲,并将其应用到多智能体系统一致性研究中,从而提出了一类随机脉冲控制下多智能体系统一致性的分析方法。
(2)借助Lyaponov函数稳定性和时滞动态系统比较定理的分析方法,获得了随机脉冲控制下时变时滞多智能体系统一致性的充分条件。
1 相关定义与引理
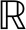
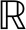
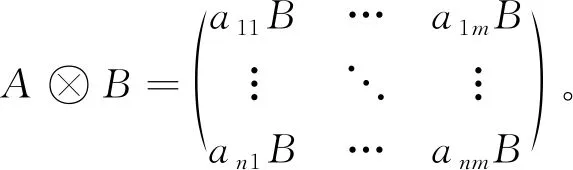
(1)
T
(ε
)表示矩阵的集合,使得每一行的元素之和等于实数ε
。集合M
定义如下:如果M
=(M
)×∈M
,M
的每一行正好包含一个元素1和一个元素-1,而所有其他元素都是零。j
1(j
2)表示每i
行中第一个(第二个)非零元素的列索引。集合H
的定义是H
={{j
,j
},{j
,j
},…{j
1,j
2}}。集合M
定义如下:M
⊆M
并且如果M
=(M
)×∈M
,对于任何一对列索引j
和j
,存在索引j
,j
,…j
,其中,j
=j
且j
=j
,这样对于m
=1,2,…,l
-1,有{j
,j
+1}∈H
。考虑如下随机脉冲控制下的多智能体系统:
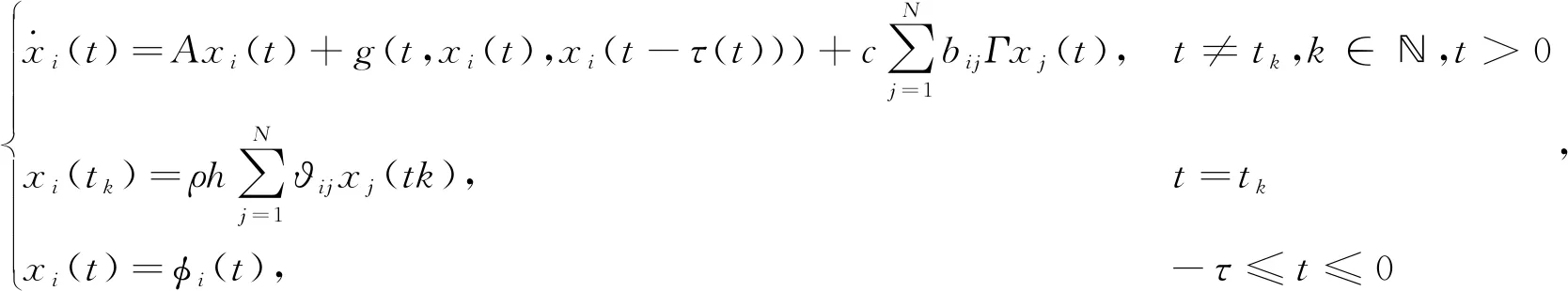
(2)
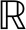
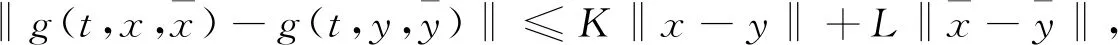
(3)
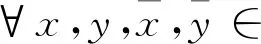
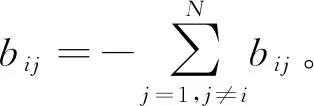
(4)
假设系统(2)的初始条件由式(5)给出
x
(t
)=φ
(t
),-τ
≤t
≤0,i
=1,2,…,N
,(5)
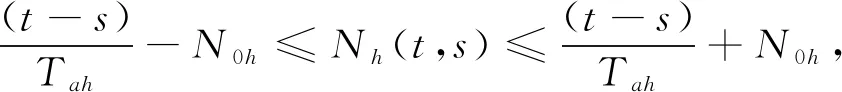
T
h
>0,N
0>0,那么T
和N
0分别称与模态相依的脉冲间和第h
种脉冲强度(h
=1,2,…,δ
)的弹性数。定义
2如果存在
ε
>0,T
≥0和M
>0使得‖x
-x
‖≤M
-,t
≥T
,任意i
,j
=1,2,…,N
,则在初始条件(5)下,多智能体系统(2)可以达到一致。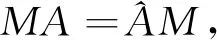
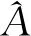
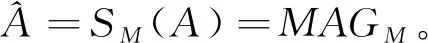
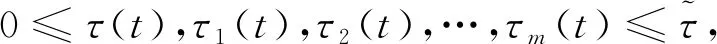
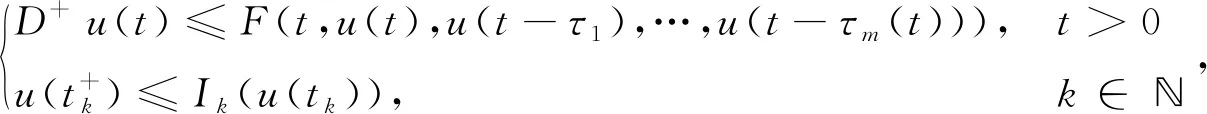
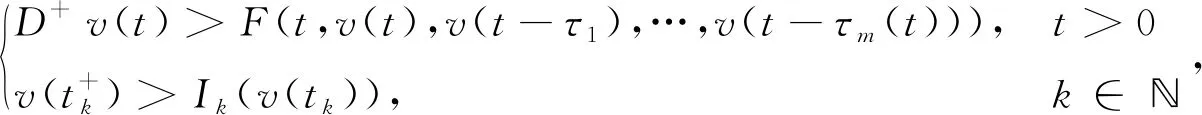
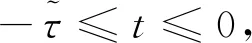
引理
322对于任意矩阵
A
、B
、C
和D
,它们的Kronecker积具有以下特性:(1)(μA
)⊗B
=A
⊗(μB
),其中μ
是一个常数;(2)(A
+B
)⊗C
=A
⊗C
+B
⊗C
;(3)(A
⊗B
)(C
⊗D
)=(AC
)⊗(BD
)。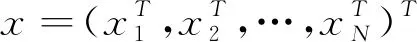
2 多智能体系统的随机脉冲控制
用Kronecker积的形式可以将式(2)表示为
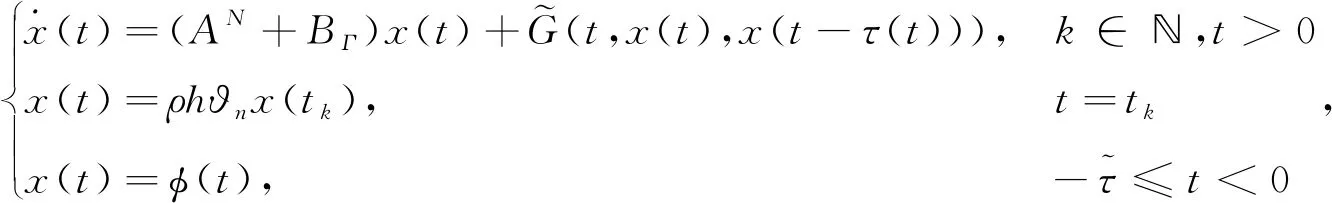
(6)

为了简化表述,现给出一些符号如下
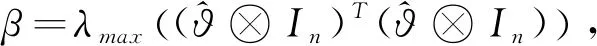
(7)
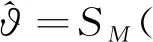
定理
如果存在一个P
×N
阶矩阵M
∈M
,以及满足假设1和定义1的υ
和T
,使得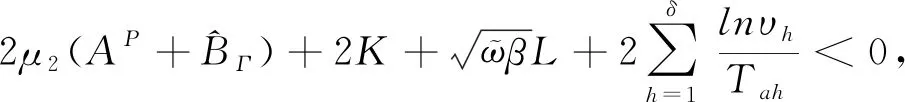
(8)
那么式(2)一致满足
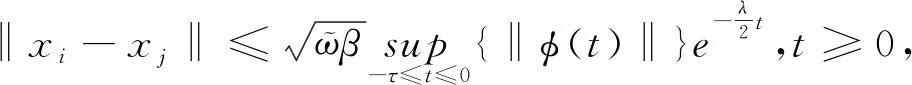
(9)
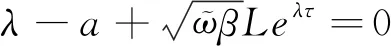
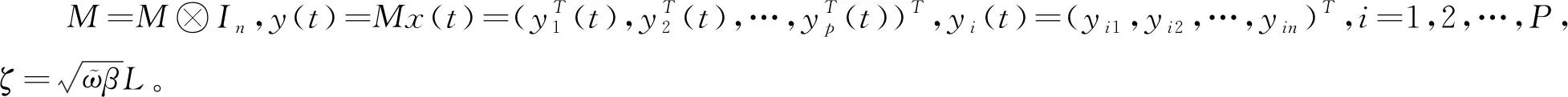
构建一个Lyapunov函数如下:
V
(x
)=x
M
Mx
。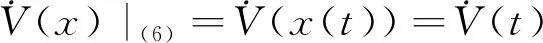
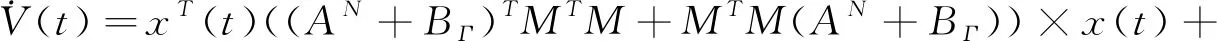
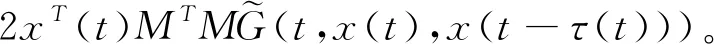
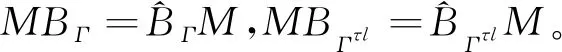
因此,
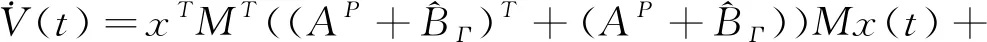
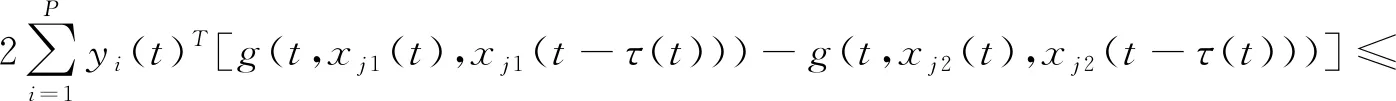
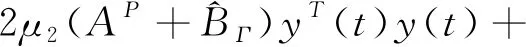
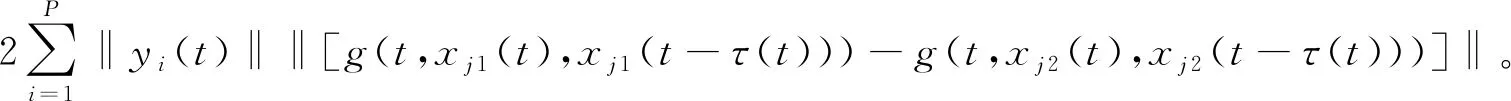
由式(3)得
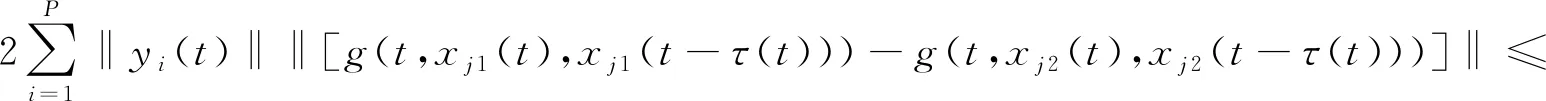
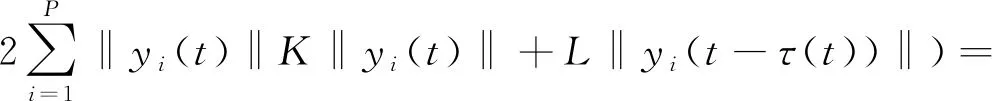
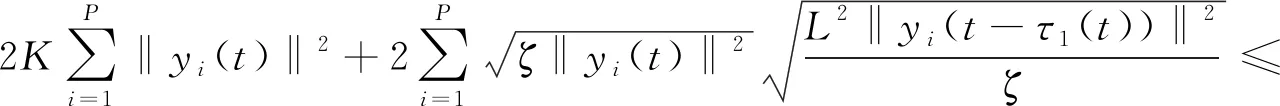
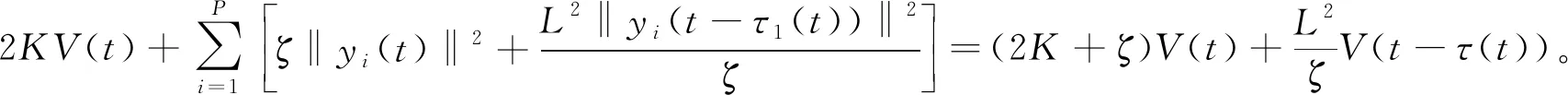
t
∈(t
-1,t
],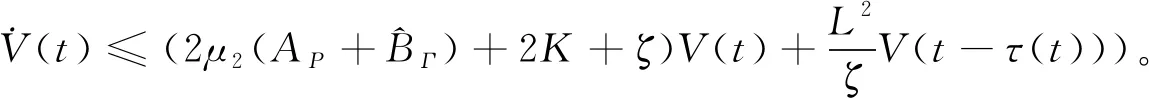
t
=t
,V
(t
)=x
(t
)(ρ
ϑ)M
×M
(ρ
ϑ)x
(t
)=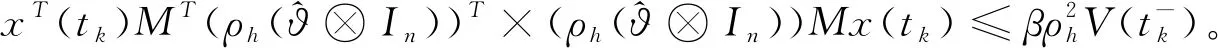
不等式两边取期望,得
ε
>0,令ν
(t
)为如下脉冲系统,即式(10)的唯一解。根据引理2,对于任意t
>0,有ν
(t
)≥V
(t
)≥0。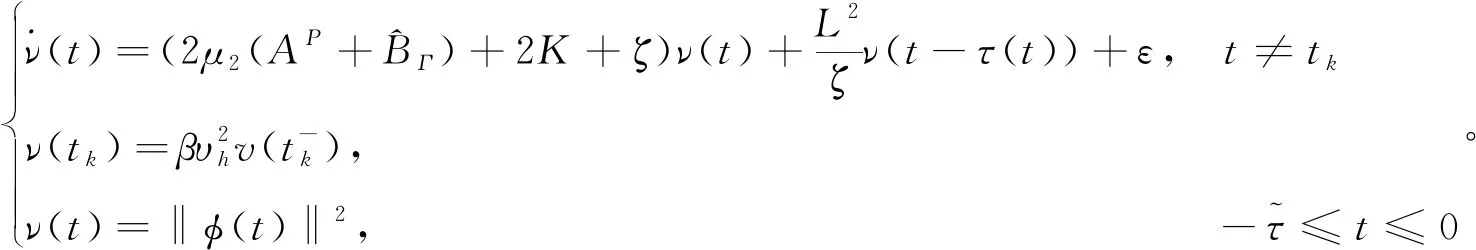
(10)
式(10)的解为
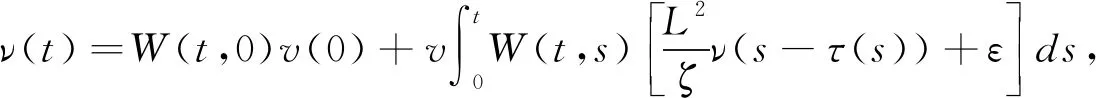
(11)
式中,W
(t
,s
)(t
,s
≥0)就如下方程的解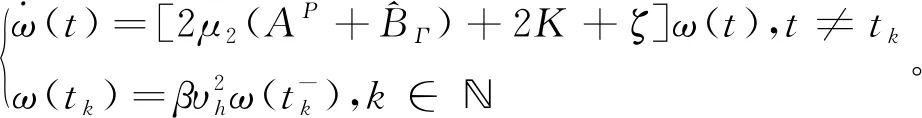
根据定义1,我们可以得出
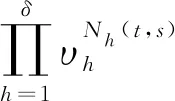
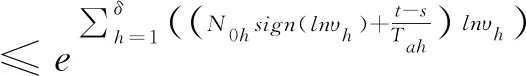
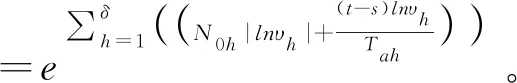
t
≥s
≥0,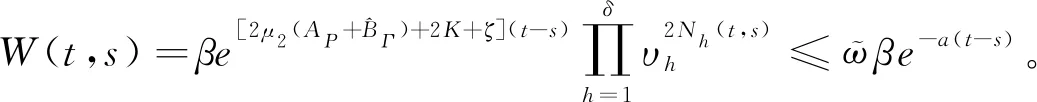
γ
=ϖβsup
-≤≤0{‖φ
(t
)‖},则对于任意t
≥0,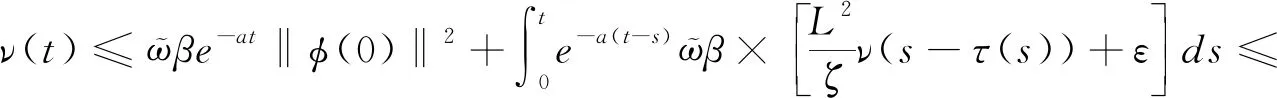

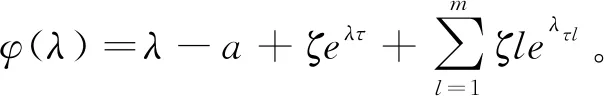
ε
,λ
,a
-ζ
>0,有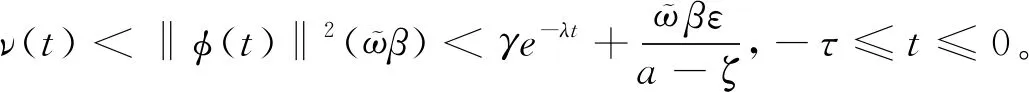
那么,可以通过反证法证明如下不等式
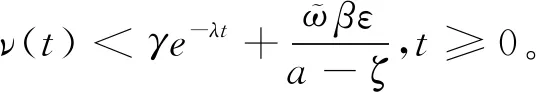
(12)
如果式(12)不成立,则存在一个t
满足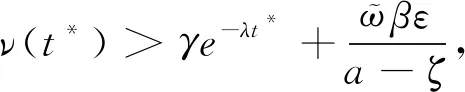
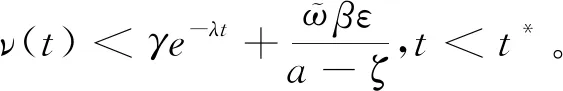
由此,通过下述证明,可以推出一个矛盾

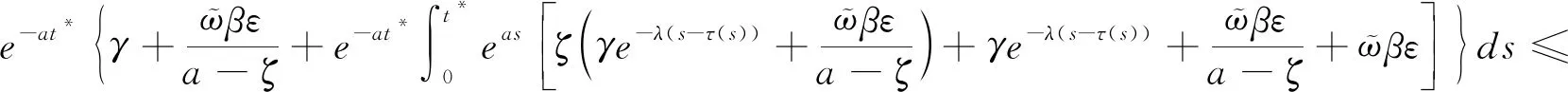
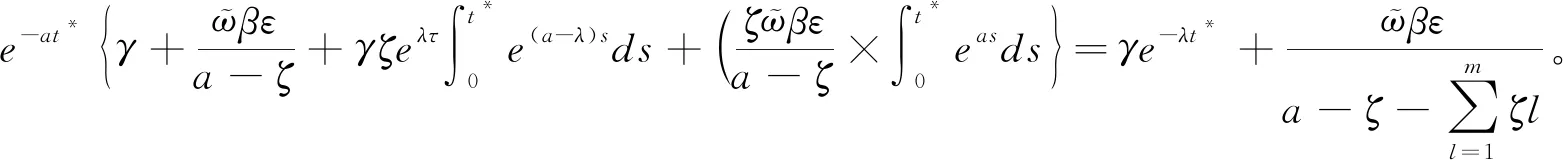
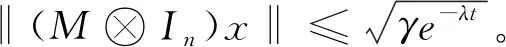
注:研究在引入随机参数来刻画随机脉冲后,通过时滞动态系统比较定理,最终分析得出了定理1中随机脉冲控制下可以使用多智能体系统,即式(2)达到一致的充分条件。
3 结论
研究随机脉冲控制下时变时滞多智能体系统的一致性。考虑到实际应用中一些随机因素对脉冲控制器的影响,引入随机参数来刻画脉冲发生强度。然后通过时滞动态系统比较定理,借助Lyapuno函数工具,获得了随机脉冲控制下时变时滞多智能体系统一致性的充分条件。
