基于Hough变换的花式织物纹样修正

潘苏情，朱 昊

(绍兴文理学院 纺织服装学院，浙江 绍兴 312000)

随着网络技术的发展和普及，数字化技术在纺织领域的发展也越来越广泛，如检测机织物密度、检测织物疵点、模拟机器运行等等。在纺织品纹样设计或来样加工中，需要扫描或拍照上传图像，然而由于试样摆放、拍摄角度或织物自身的原因等，无法绝对地保证横向水平和纵向竖直的状态，即使事先经过人工手动调整，织物图像的偏斜也无法避免。而且由于现有的大部分织物组织分析等算法都对图像倾斜较为敏感，倾斜角度的存在会给识别结果造成较大误差，检测速度也较缓慢，因此，有必要寻求一种准确修正织物图像的办法。

经查阅文献发现，图像几何校正技术在纺织领域已成为研究热点。如潘如如等提出一种利用图像纹理特征实现机织物图像的纠偏方法，由于机织物的纱线是平直的，两根纱线之间的距离与纱线方向相同，只要能对纱线的间隙进行倾斜纠正就可以实现织物图像的纠偏；或者通过傅里叶变换提取图像不同位置直线信号的周期，以周期性最强的直线信息作为判断织物图像中纱线位置的标准，并依此实现了高紧度机织物图像的倾斜纠正。吴海虹等利用图像梯度作为纬纱的走向信息，运用层次Hough变换检测纬纱偏斜角度。

虽然已有大量研究证明图像几何校正技术不管是用于机织物、针织物还是非织造织物，都有所进展和突破，基于的算法也不局限于一种，但是基本上都只适用于同类织物。因此，本研究想寻求一种可同时适用于机织物和针织物的花式织物纹样修正算法。研究采用Canny算子检测图像边缘，Hough变换检测直线，根据横向和纵向的倾斜角对图像进行仿射变换修正。Hough变换主要优点是能容忍特征边界描述中的间隙，并且相对不受图像噪声的影响。此方法不仅能快速将花式织物花型纹样修正，提高工作效率，而且对后续图像检测影响较小，大大提高了图像的准确度。

1 花式织物纹样修正算法设计

Python语言是一种解释性语言，代码简洁明了，上手容易，其拥有各种各样的工具库，若无特殊要求，不需要自己重新编写，即可直接调用，研究中就采用了opencv、numpy、skimage、math、copy、matplotlib等库来进行图像的处理以及多维数组的运算。

研究对倾斜的花式织物进行修正，在扫描图像后，为了突出图像的特征，需要将图像进行灰度化和边缘检测。合适的边缘检测可以减少Hough变换的运算量并增加后续操作的准确度，所以，研究对现有的几种边缘检测方法进行了分析比较，最后决定采用Canny边缘检测算法更为恰当。经过边缘检测后的图像线条明显突出，此时可以采用Hough变换。由于需要同时考虑机织物和针织物的适用性，而针织物线圈横列不一定平行于水平方向，线圈纵行并不一定平行于垂直方向，线圈横列不一定垂直于线圈纵行，所以Hough变换的结果需要分别得到横向和纵向的直线倾斜角度，且普通的旋转变换不能满足要求，需要采用仿射变换进行图像修正。由于Python语言中，修正后图像仍处于矩形画布中，除修正图像以外部分被涂黑，此时需对画布进行裁剪从而得到面积最大图像，最后输出裁剪后的图像即为最终修正结果如图1所示。

图1 花式织物纹样修正算法设计流程

2 数字图像处理

2.1 图像灰度化

一个图像由若干个像素点组成，像素点是图像最小的单位，每个像素点的颜色由R(红色)、G(绿色)、B(蓝色)3个值确定。图像灰度化就是使图像中的每一个像素点都满足R=G=B，这个相等的值称为灰度值。最基础的图像灰度化方法有：最大值法、平均值法、加权平均法。

由于最大值法和平均值法较为简单，且没有考虑亮度通道信息。而加权平均法是将R、G、B 3个值以不同的权值进行加权平均，以此得到的值作为灰度值，将图像灰度化。因此，研究采用加权平均法将图像灰度化。

2.2 图像边缘检测

Poggio提出，边缘或许对应着图像中物体(的边界)或许并没有对应着图像中物体(的边界)，但是边缘具有十分令人满意的性质，它能大大地减少所要处理的信息但是又保留了图像中物体的形状信息。图像的边缘检测就是为了使图像的轮廓更加明显，突出图像的特征的图像处理办法。对现有边缘检测算法，研究分析比较了Laplacian、Sobel和Canny三种边缘检测算法。

Laplacian算法是最简单的各向同性微分算子。各向同性就是无方向性，可以对任何方向进行加强，但其实也得不到任何方向的信息。所以Laplacian算法特别适合用于突出图像中的孤立点、孤立线或线端点，只是其对噪声比较敏感，所以很少用该算子检测边缘。

Sobel算子用于提取边缘，简单快速，对灰度渐变、噪声较多的图像处理效果较好。然而，Sobel算子通过像素平均抑制噪声后，检测出的图像边缘不止一个像素，不能检测出真正的边缘，所以提取的图像轮廓可能会与背景融为一体。

Canny边缘检测只需要处理部分数据量，而且还可以有效提取所需的信息。根据图像设定高低阈值，假如边缘像素的梯度值高于高阈值记为强像素点；介于高低阈值之间记为弱像素点；小于低阈值则舍去。所以Canny算子可以检测出真正的边缘，识出的边缘要更接近图像中的实际边缘。

机织物的边缘检测算法对比如图2所示，针织物的边缘检测算法对比如图3所示。对比三种边缘检测方法，可以明显看出Laplacian边缘检测没有突显边缘，且图像噪声对图像的影响较大；Sobel边缘检测时，原图中颜色相近的区域没有检测出来，即不能严格区分出图像与背景；而Canny边缘检测的效果较好，边缘特征突出，边缘检测完整，有利于下一步操作。

综上所述，研究最终选择采用Canny边缘检测算法，其对机织物和针织物的边缘处理效果都不错，可得到更接近实际的边缘。

图2 机织物的边缘检测算法对比

图3 针织物的边缘检测算法对比

2.3 Hough变换

Hough变换最早是从黑白图像中检测直线，后来的广义Hough变换则可以检测任何曲线。其所实现的是一种从图像空间(直角坐标系)到参数空间(极坐标系)的映射关系。利用点与线的对偶性，可将图像空间的检测问题转换到参数空间解决。

Hough变换原理如图4所示。由图4可知，若需要检测出直角坐标系中的直线

L

，并求其倾斜角，则将直角坐标系中每一个点转换成极坐标中的曲线。此时发现

A

、

B

、

C

、

D

、

E

、

F

点转换到极坐标系中分别为曲线

L

1、

L

2、

L

3、

L

4、

L

5、

L

6，其中有5条曲线相交于

K

点，

L

6也与其他5条曲线有交点，但是交于

K

点的直线更多，说明

K

点对映的直线才是所需检测的直线，此时可根据

K

点坐标得出直线倾斜角。

(1)

(2)

k

=

max

(

max

(

a

)),

(3)

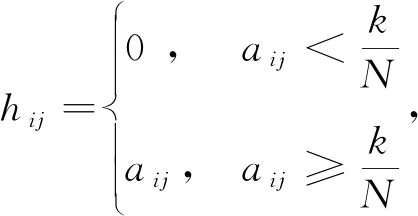
(4)

(5)

max

(

sum

)= ∑=1～

a

,

(6)

θ

=

b

1。

(7)

图4 Hough变换原理

2.4 仿射变换与图像裁剪

仿射变换是将一个平面的点映射到另一个平面内的二维投影，包括平移、旋转、放缩、剪切等，具有很强的实用性，可用于图像配准、图像纠正和纹理纠正，以及创建全景图像等。其保持了二维图形的“平直性”，即仿射变换前平行的两条直线，仿射变换后仍然是直线且平行，所以不会改变织物的花型，效果较好。

仿射变换是一种二维坐标(

x

,

y

)到二维坐标(

u

,

v

)的线性变换，其数学表达式如式(8)所示。

(8)

对应的齐次坐标矩阵表示为

(9)

由上述矩阵可得，若已知仿射变换前的三点及其对应的变换后的三点，则可以确定一个仿射变换矩阵，而且是唯一的仿射变换矩阵，从而可将整个图像进行仿射变换修正。由于织物的摆放、拍摄角度或织物自身的原因等，导致纵横向存在多种倾斜情况，可能会得到不同的变换矩阵，需要分情况讨论。

研究算法中，图像的仿射变换经过旋转和平移。将旋转中心设定为图像中心，由于图像的大小和横纵向倾斜角度已知，图像旋转前后的坐标可根据几何运算求得。以某一横纵向倾斜情况为例(见图5)，选图像中心(

P

1)、经过

P

1的纵向倾斜直线与图像上边界的交点(

P

2)和经过

P

1的横向倾斜直线与图像左边界的交点(

P

3)，以这三点的位置及其对映旋转并平移后三点(

P

1′、

P

2′、

P

3′)的位置确定仿射变换矩阵。

图5 仿射变换和画布扩大

原矩形图像经过仿射变换后变为平行四边形图像，而由于

Python

中坐标值为负的图像部分不显示，所以为了得到完整的变换图像，需要对图像画布进行扩大。由于旋转前后图像均具有对称性，所以可根据原矩形图像两顶点(

Q

1、

Q

2)及仿射变换矩阵，得到平行四边形图像突出正坐标系的两顶点(

Q

1′、

Q

2′)坐标，从而得到横纵向伸出长度，将图像画布扩大，得到完整的图像。此时，画布为矩形，而不存在图像的部分被涂黑，影响美观和后续操作，需要将图像裁剪为矩形，裁剪需知矩形的两个坐标(左上角坐标及右下角坐标)。研究采用中心扩散的算法对图像进行裁剪(见图6)，即从中心点

H

出发，逐渐向两边延伸，每增加1个像素点，就经过此时的

M

点和

N

点分别作垂线交平行四边形上边界于

G

点和

R

点，直到无法同时存在

G

点和

R

点时停止延伸。若同时存在

G

点和

R

点，比较两交点纵坐标(

y

1和

y

2)的大小，选择较大的纵坐标(

y

2)，根据对称的原理很容易得到

T

点纵坐标

y

3。此时根据

S

点和

T

点坐标可计算矩形面积，每一次得到的面积都与上一次得到的面积作比较，得到最大面积时的两个点(

S

点和

T

点)坐标即为最终裁剪所需坐标。经过试验证明，只要仿射变换正确，此算法基本上就可以得到最大面积的裁剪图像且操作方便快捷，裁剪效果良好。

图6 图像裁剪

3 花式织物图像修正效果

为验证算法的可行性，将同一机织物或针织物手动摆放若干不同角度测试修正效果(见图7、图8)。实验证明，该算法可同时运用于机织物和针织物，在允许范围内的任意倾斜角度下都可以进行修正。

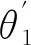
图7 机织物不同倾斜角度修正图像

图8 针织物不同倾斜角度修正图像

4 总结

研究算法旨在寻求一种可同时适用于机织物和针织物的花式织物纹样修正算法，此算法减少了确定阈值的步骤，自动得出横纵向倾斜角度，仿射变换后裁剪得当，效率高，效果好，可行性较高，但同时也存在较大局限，后续算法可考虑从以下方面改进：

(1)二维图像的花型纹样中线条较多时会对Hough变换检测结果产生干扰，如导致检测出的角度为花型纹样角度而不是纵横向倾斜角度，可考虑在忽略纹样并突出纵横向的情况下检测。

(2)拍摄或扫描的图像可能存在扭曲现象，如图像纵横向不一定是直线，可能是弯曲的曲线时，Hough变换效果不好，后续可考虑直线分段修正算法。

表1 不同样品的修正效果