二次域中类数h(k)=1时丢番图方程整数解探讨

王 振 谢 清

（安徽文达信息工程学院，安徽 合肥 230039）

定理1.1[1]：设K为一个二次域，则必有对于K的代数整数环 kO 有：当

当时，

定理1.2[3]：设K是代数数域，OK为K的代数整数环，且类数为h(k),则：

定理1.3[1]：设M满足唯一分解整环，从而对于整数k≥2以及α,β∈M(α,β)=1，当αβ=γk.k∈M时，必有：

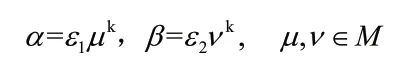
其中ε1,ε2两个元素是M中的单位元素，而且ε1ε2=εk。

1 主要结论证明

证明方程1

无整数解。

分解（1.1）式可知：

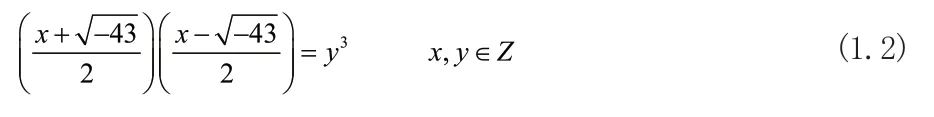
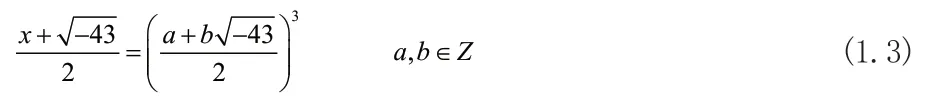
整理等式（1.3）可得：

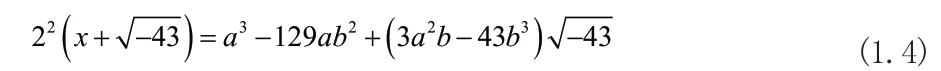
由等式性质比较两边系数易知：

若b=±1，代入2.6式得，与矛盾。

若b=±2 , ± 22由于a≡b(mod 2)同奇同偶，从而由等式(1.6)式得：

综合以上证明可知方程(1.1)无整数解。

证明方程2

无整数解。

分解（1.7）式可知：

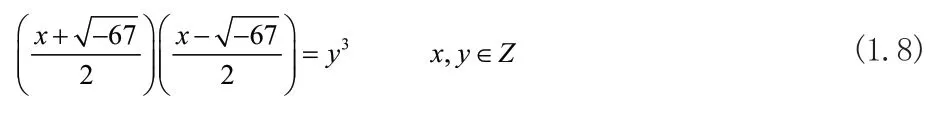
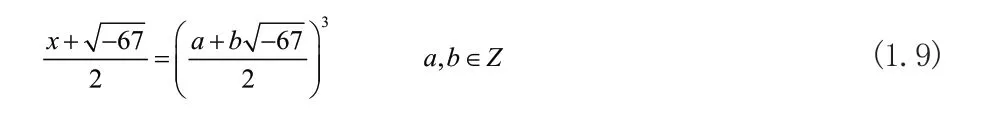
整理等式（1.9）可得：

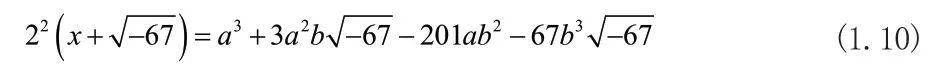
由等式性质比较两边系数易知

由等式（1.12）式知：b=±1 ,±2 ,± 22

若b=±1 ，代入（1.12）式可得3a2= 63或71，显然a∉Z与a Z∈ 矛盾。

若b=±2 , ± 22由于a≡b(mod 2)同奇同偶，从而由1.12式得：

左边22≡22(mod 23)右边b(3a2-67b2)≡0 (mod 23) 矛盾

从而丢番图方程(1.7)式无整数解。