模糊环境下考虑供应中断的再制造闭环供应链研究

王 振，郭健全

(上海理工大学 管理学院，上海 200093)

近些年，随着人们环保意识的增强和环保立法体系的健全，再制造作为环境保护的一项手段，愈来愈为人重视[1-3]。再制造是将废旧的产品进行回收，然后在原先的基础上进行新的生产制造。因此，再制造可以大大降低企业的成本[4-5]。然而，在再制造供应链系统中，诸如市场需求量、回收品质量、供应商供应情况等因素都是不确定，这便极大地增加了再制造供应链系统的复杂性[6-7]。

再制造面临许多挑战，诸如企业对废旧品回收的意愿、消费者对再制造产品的认可。这些挑战最终将导致再制造产品的需求量和回收品质量具有不稳定性和不确定性[8]。Tao等[9]在市场需求不确定的前提下给出了生产商最优再制造策略。Galbreth等[10]在需求不确定的情况下研究了最优回收与再制造策略。Zhou等[11]建立了当市场需求不确定下的再制造供应链模型，并分析需求不确定的影响。Wu等[12]分析了多种质量等级的回收品回收价格，认为不同质量等级的回收品对回收价格的敏感程度也各不相同。以上分别研究了市场需求和回收品质量的不确定性问题，许多情况下，上述不确定性经常是同时存在的。基于此，本文同时考虑需求与回收质量的不确定。

模糊规划法是解决闭环供应链不确定性问题的重要方法之一[13]。Su[14]构建了不同约束条件下再制造系统的模糊优化模型，通过检验得出了模糊约束规划方法能解决再制造单个不确定性问题的结论。Guchhait等[15]采用模糊规划法解决回收时需求量不确定的问题。Hilger等[16]考虑了需求不确定性条件下的制造/再制造混合系统，并采用模糊规划法解决了这一问题。Yadav等[17]提出了用模糊规划法来解决制造商回收时回收质量不确定的问题。以上模糊规划方法是对不确定性进行单独研究的，本文基于对供应链系统的分析，运用模糊机会约束规划方法同时考虑了市场需求量和回收品质量水平的不确定性问题。

供应中断问题越来越受到从业人员的重视[18]。Zhu[19]研究了企业在需求不确定情况下的供应中断问题，并制定了相应的策略，以最大限度地降低采购成本。面对供应风险，Kamalahmadi等[20]用决策树法来解决不同需求下的中断场景。考虑到供应中断，Li等[21]考虑不同回收质量下中断发生的可能性，并制定了相应的策略。以上研究很少将供应中断风险与市场和回收质量不确定联合起来考虑。因此，本文在考虑市场需求和回收质量不确定的基础上，分析了供应中断对再制造闭环供应链的影响，并提出了解决此问题的最优方法。

基于以上分析，本文在需求量和回收品质量模糊不确定的假设前提下，构建了考虑供应中断的再制造闭环供应链总成本模型。并且利用三角模糊变量描述市场需求量不确定性和回收品质量不确定性，然后利用模糊机会约束规划解决模型不确定性问题。同时将供应中断概率设为变量，并采用启发式算法如PSO (particle swarm optimization)算法和GA (genetic algorithm)算法来寻找算例的最优解。本文的研究有助于企业在需求和回收质量模糊不确定的情况下针对不同的供应中断情况制定相应的策略，以达到最优决策的目的。表1为以上文献资料和本文的对比情况。

表 1 文献总结Table 1 Literature summary

1 模型假设与函数构建

1.1 模型假设

1) 需求率和回收品质量未知；

2) 再制造品和新产品包装、售价均相同；

3) 回收品能全部用于再制造[22-23]；

4) 不考虑丢弃、提前期和缺货[24]。

1.2 函数构建

1.2.1 需求和回收质量模糊函数

为有效规避模糊不确定参数的影响，宜采用模糊机会约束规划方法(fuzzy chance constrained programming, FCCP)[25]。模糊隶属函数见图1。将Di看作需求量模糊数，Qi看作回收质量模糊数。记Di=(Di1,Di2,Di3),Qi=(Qi1,Qi2,Qi3)，t为三角模糊集。其模糊隶属函数表示如下

图 1 模糊隶属函数Figure 1 Fuzzy membership function

在探讨清晰化问题之前，提出以下定义：

Ad、Aq分别表示需求量和回收质量不确定时的置信水平。

1.2.2 再制造成本函数

2 系统模型

本文建立了模糊环境下的再制造闭环供应链模型，消费者需求由制造品库存和再制造品库存共同满足。制造商购买原材料生产产品，再制造商将回收来的废旧品进行再制造。再制造系统中包含3种库存，分别是包含制造品库存和再制造品库存的可用库存、原材料库存和回收品库存，物料流动方式如图2。

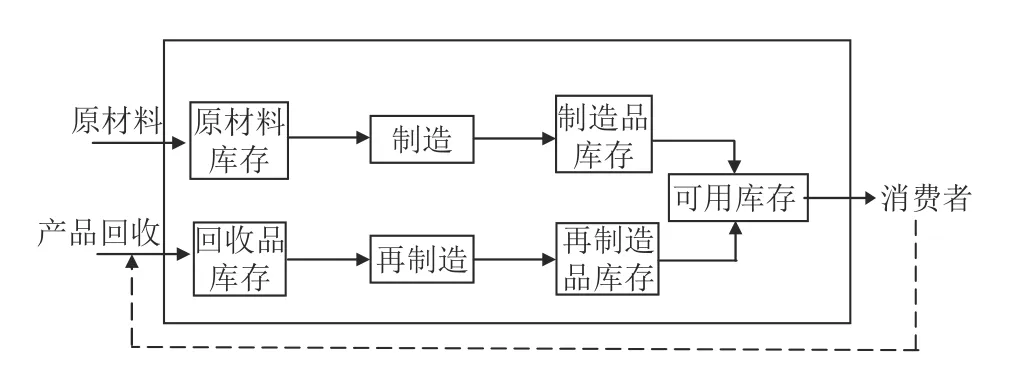
图 2 物料流动Figure 2 Material flow

2.1 库存水平

假设一个周期T中包含n个制造期Tn和m个再制造期Tm，则mDTm=dT，nDTn=DT−dT。回收品、制造品和再制造品的物流方式如图3所示。

库存水平如图4所示，该模型先考虑再制造过程，再进行制造过程。假定再制造率为(1/γ)D，制造率为(1/β)D，并且γ＜1，β＜1。首先，再制造品库存以(1/γ −1)D的速率上升，回收品库存以(α−1/γ)D的速率下降。然后，制造品库存以 αD速率上升，原材料库存以(1/β)D的速率下降[28]。

图 3 物料流动Figure 3 Material flow

图 4 库存水平(m=2,n=2)Figure 4 Inventory levels (m = 2, n = 2)

根据以上分析及图4，T=mTm+nTn，mDTm=αDT，nDTn=(1−α)DT，mIM=(1−γ)αDT，计算可得：IM=(1−β)(1−α)DT/n；IR=(1−γ)αDT/m；Ir=α[(1−α)+α(1−γ)/m]DT；Iraw=nDTn=(1−α)DT。

2.2 平均库存持有成本

设Hm为再制造品的平均库存持有成本，Hn为制造品的平均库存持有成本，Hr为回收品的平均库存持有成本，Hraw为原材料的平均库存持有成本。hs是单位时间可用库存持有成本，hr是单位时间回收品库存持有成本，hraw是单位时间原材料库存持有成本[28]。

2.3 平均总成本

平均制造成本：V4=(1−α)DCn；平均订购成本：V5=Co/T；平均原材料成本：V6=(1−α)DCraw；平均准备成本：V7=(mSm+nSn)/T；其中，Sm为再制造准备成本；Sn为制造准备成本[28]。供应商的原材料供应中断的平均成本：V8=(1−ω)(1−α)Dd1+(1−α)ωDd2。 ω为中断概率。V1、V2公式见1.2.2节。

经过简单的推导和计算，将α=(1−ae−θp0)be−φQ代入平均总成本函数得

3 算例分析

3.1 粒子群算法

3.2 遗传算法

遗传算法(GA)是基于生物学中优胜劣汰的进化规律的一种进化算法原理[32-35]。遗传算法首先将问题参数编码成染色体，然后对染色体进行迭代选择、交叉和变异，从而对种群中染色体的信息进行交换，以生成满足优化目标的染色体的一种方法。因为变异操作是从种群中随机选择一个个体，从个体中选择一个点进行变异，因此产生更好的个体。个体基因Bij的突变操作方法为

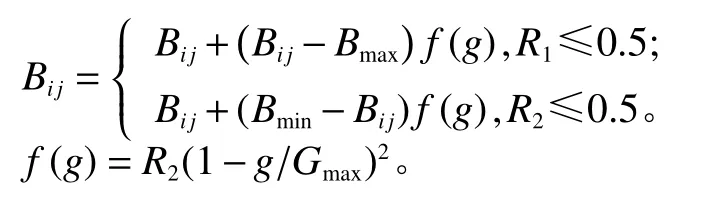
其中，Bmax是基因Bij的上界，Bmin是下界；g是迭代次数，Gmax是最大进化次数，R1、R2是[0,1]区间的随机数。

3.3 置信水平敏感性分析

根据实际情况进行模拟运算，给出企业再制造回收时的需求量与回收质量的三角模糊数，如表2所示。

其中，市场需求量和回收质量水平随置信水平的变化而变化。为了分析置信水平对最优策略的影响，本文采取均匀分布设计法对置信水平赋值，并按10%极差，分别对Ad、Aq赋值70%、80%、90%。在此基础上，对两类置信水平进行交叉从而产生9种情况并代入模型中，运用Matalab软件编写GA和PSO代码，迭代计算后的目标值如表3。

表 2 需求量与回收质量的三角模糊数Table 2 Triangular fuzzy numbers of demand and recovery quality

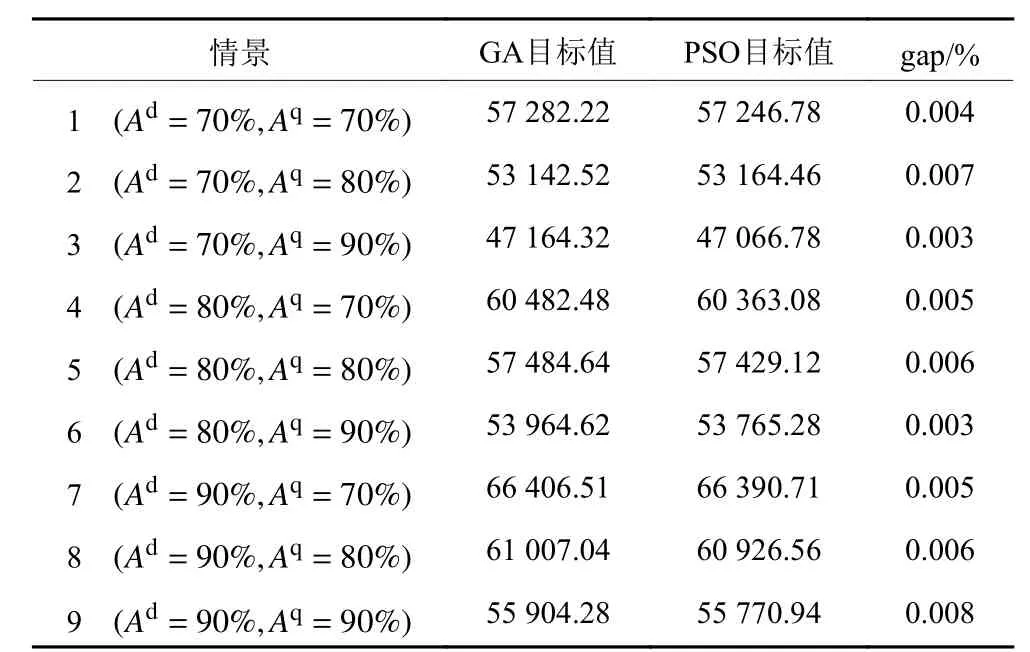
表 3 不同置信水平的目标函数值1)Table 3 Objective function values for different confidence levels

在敏感性分析的基础上，为实现总成本最低的目标，分别对Ad、Aq赋值70%和90%，即当需求量为1 034，回收质量为0.39时达到最优。在预设的最大迭代次数即200代下，GA和PSO分别在第153代和第175代获得最优适应度曲线。由表3可知两种算法的结果偏差未陷入局部最优，因此验证了模型的可信性和有效性。

由表3可知，目标值随Ad置信水平的增加而增加，而随着Aq置信水平的增加而减少。即当需求量一定的情况下，回收质量越高，目标值越小。这是由于当回收质量越高时，再制造成本反而越低，因此平均总成本即目标值越低。而当回收质量一定的情况下，需求量越高，目标值越大。这是由于当需求量越高，回收量相应越高，制造商要保证满足订货需求就需要保持较高的库存水平，进而带来较高的库存成本，因此平均总成本即目标值越高。因此，再制造闭环供应链上的企业应该根据不同的市场环境制定合理的、符合企业发展的生产计划。

由表4和图5可以看出，随着供应中断概率的增加，平均总成本也是逐步递增的。这是因为当供应中断发生时，企业的运作会在一定程度上受到影响，这会给企业带来严重的损失。因此，企业需要制定并实施有效的防范策略，从而避免供应中断风险的发生，以使企业正常的生产运作得以顺利进行。

表 4 不同供应中断概率 ω的灵敏度分析Table 4 Sensitivity analysis of different supply interruption probability

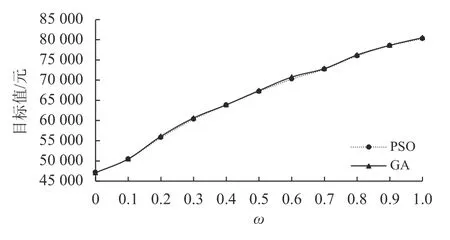
图 5 不同供应中断概率下的总成本波动图Figure 5 Graph of total cost fluctuations under different probability of supply disruption

4 结论

本文在市场需求和回收品质量水平模糊不确定的前提下，构建了考虑供应中断风险的再制造闭环供应链的总成本模型。运用算例，利用模糊机会约束规划解决模型不确定性问题，将供应中断概率设为变量，并采用启发式算法如PSO算法和GA算法来寻找算例的最优解。计算结果表明：不同需求量和回收品质量的组合下企业的成本有不同的变化；供应中断的发生会影响整个供应链系统，为企业的正常运作带来较大的不便，从而使企业蒙受损失。因此，再制造闭环供应链上的企业在面临需求量和回收品质量模糊不确定的市场环境时，应尽量避免供应中断，制定符合企业发展的运作计划，以达到最优决策。