基于Elman神经网络的联合循环机组燃烧室温度模型建模

窦征立，王亚刚

(上海理工大学 光电信息与计算机工程学院，上海 200093)

天然气储量丰富，具有热值高、燃烧产物对环境污染较小等优点，工业和生活需求量日益增多，这也使得燃气-蒸汽联合循环发电机组总装机容量逐年增加[1-3]。因此，对燃气-蒸汽联合循环发电机组系统模型建模则变得越来越重要。但是燃气-蒸汽联合循环发电机组非线性和强耦合的特点，使得燃气轮机的负荷在快速变化时，一些参数的快速变化会导致主蒸汽压力发生变化，影响发电机的出力，同时也会反过来影响联合循环机组的整体负荷，进一步影响供热品质。

神经网络[4]的计算能力通过其大规模并行分布式结构以及其学习能力和由此带来的泛化能力来体现。同时，神经网络也具有非线性、输入输出映射、容错性等优良特性。Elman神经网络具有良好的非线性动态特性，可以对时间序列数据上一时刻的输入输出数据进行充分地学习，以便对下一时刻的输出进行预测。本文将对燃气-蒸汽联合循环机组燃烧室模型进行建模。

1 燃气-蒸汽联合循环发电机组温度模型

燃气-蒸汽联合循环发电机组[5]通常由燃气轮机、蒸汽轮机、余热锅炉等设备组成。燃气轮机在整个联合循环发电机组中起着关键作用[6]，一般由压气机、燃烧室、透平三大部件组成。燃烧室在燃汽轮机中起到了承前启后的作用。

燃气轮机主控制系统[7]包含有燃气轮机的启动控制系统、转速控制系统、加速度控制系统、温度控制系统、停机控制系统和手动FSR(Fuel Stroke Reference)控制系统，这些控制系统通过改变FSR值来改变燃料量的输入。燃气轮机温度控制系统通过比较燃机的排气温度与温度控制参考值的结果来改变FSRT(Fuel Stroke Reference Temperature)。当排气温度高于所设定的温度控制参考值时，燃气轮机机组将降低FSRT的输出，使得排气温度下降到温度控制参考值；当排气温度低于所设定的温度控制参考值时，FSRT增加并超过转速燃料行程基准FSRN(Fuel Stroke Reference N)，温度控制器系统退出控制。因此，温度控制系统是最高温度限制系统。

燃烧室内部工质做功过程为：从压气机出来的压缩空气进入燃烧室与气体燃料进行混合并燃烧，产生的燃气流动至燃烧器出口。本文所建立燃烧室模型的工质流动界限为压气机出口和透平进口的物理边界作为控制对象的界限。假定燃烧室内部焓值、压力和温度均匀分布，燃烧室模型可简化为一个混合反应室，内部工质作为理想气体处理，反映燃烧室动态变化过程关系主要为质量守恒定律和能量守恒定律。因此，根据以上关系建立微分方程来反映燃烧室动态变化过程。其质量守恒方程为

gb=(1-C)gcp+gf

(1)

Δg=gcp+gf-gb

(2)

式中，gcp为压气机出口空气质量流量；gf为燃料质量流量；gb为燃烧室燃烧产生的燃气质量流量；Δg为燃烧室的蓄质；C为损失系数。

从能量转换机理出发，其能量平衡方程[8]为

gfhf+gcphcp+gfηrQg，net-gbhb=Δghb

(3)

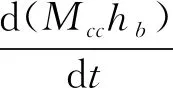
(4)

式中，hf为天然气焓值；hcp为燃烧室进口空气焓值；hb为燃烧室燃烧产生的燃气焓值；Mcc为燃烧室内部质量。

理想气体焓值计算式为

hb=cbTcc

(5)

式中，cb为燃气比热；Tcc为燃烧室出口温度。

将式(5)带入式(4)中，得到燃烧室出口温度的一阶微分方程如下

(6)

式中，τcc为燃烧室时间常数；ηr为燃烧效率，一般通过实验获取[9]，并根据效率与功率变化关系曲线来进行计算

(7)

式中，k为比热比。因此，对于燃烧室温度模型而言，其输入为最少燃料给定基准，并对应一个燃烧室温度设定值；输出为燃烧室燃烧排气温度，可以简化为一个SISO系统[10]。

2 Elman神经网络

FNN(Feedforward Neural Network)是由多个神经元、输入层隐含层以及输出层组成的网络[11]，而RNN(Recurrent Neural Network)是一类用于处理序列数据的神经网络[12]，其结构如图1所示。RNN与FNN的区别在于，RNN的反馈循环会对其过去的输出进行判定，将这一时刻的输出作为下一时刻的输入。RNN在外部序列x(t)的驱动下，系统在t时刻的状态h(t)为

在“互联网+”时代，为应对经营管理数字化、平台化的变化趋势，乡村旅游的经营管理模式应从智慧旅游管理和线上+线下+融合两方面来进行升级转变。

h(t)=f(h(t-1)，x(t);θ)

(8)

因此，RNN将系统的隐藏状态信息保存在网络中，跨越多个时间步，一层一层地向前传递，影响着网络中每一个新样例的处理。RNN优势是在多个时间步长内能够共享相同的权重。由于RNN利用了共享参数的思想，可使RNN能够对不同长度的样本进行学习并泛化。

Elman神经网络[13]是Elman J L提出的一种神经网络，其可以看作是一个具有局部记忆单元和局部反馈连接的循环神经网络，网络结构如图2所示。图中ut为输入层向量；xt为隐含层向量；ht为承接层，用来接收上一时刻结果，并作为下一时刻的输入；yt为输出层向量，输出层是一个全连接层，它的每个节点都和隐藏层的每个节点相连；W为权值矩阵。正是基于这样的特性，Elman神经网络具有良好的动态非线性效果[14]。

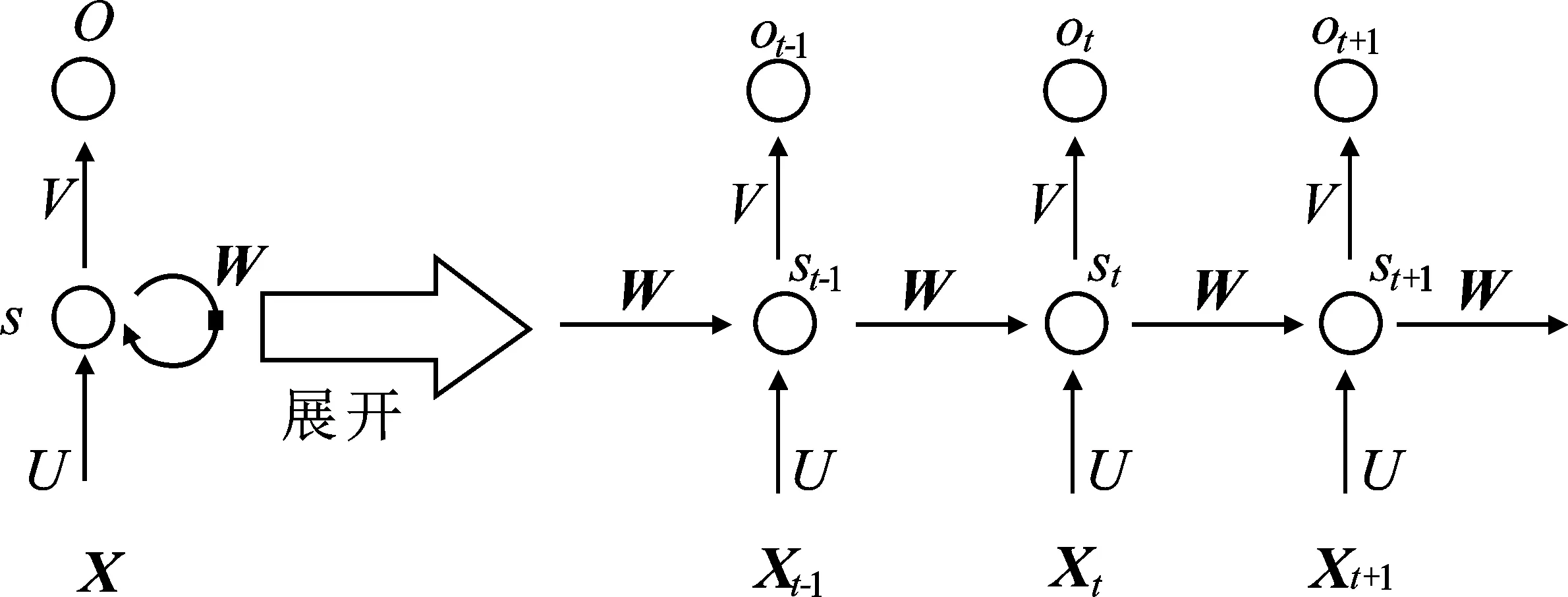
图1 循环神经网络结构图

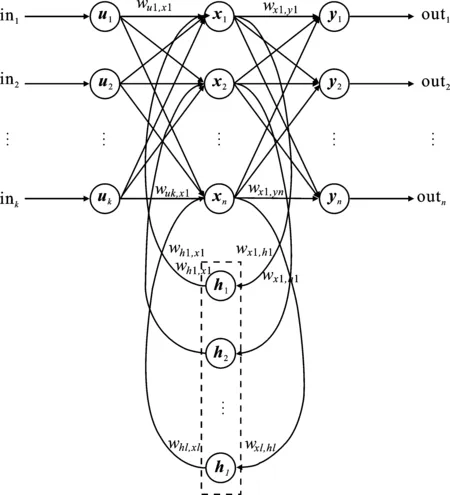
图2 Elman神经网络结构图

3 BPTT算法

BP(Back-Propagation)算法是FNN中的常用算法，一般应用于无动态特性的FNN中，而对动态网络适用性不高。BPTT(BackPropagation Through Time)算法[15]则是将网络按照时间展开，把梯度存储于每个时间步。训练神经网络是为了获得使损失函数最小的一组权值矩阵，即对W进行调整，使得损失L最小。L由式(9)表示

(9)

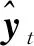
ø由图2可以看出

(10)

(11)

(12)

yt=φ(Wx，yht)

(13)

式中，ht为隐含层输出；ht为隐含层输入；ø为隐含层激活函数；Wx，y为隐含层到输出层的权值矩阵；yt为输出层输入；φ为输出层变换函数；yt为输出层输出。

在时间通道上每个时刻的梯度为

(14)

(15)

式中，Wu，x为输入层到隐含层的权值矩阵；Wx，h为隐含层到承接层的权值矩阵，k=1，…，t。

(16)

(17)

4 燃烧室温度模型建模

本文利用Pytorch深度学习框架建立了燃气-蒸汽联合循环燃烧室温度的Elman神经网络模型，其模型结构为两层Elman神经网络(64，64，1)，即输入层1个节点，2个隐含层各64个节点，输出层一个节点，整个网络偏置设为0，训练次数为1 000次，学习率为0.05，网络的损失函数为均方误差(MSE)。误差分别经BPTT算法到隐含层，并结合SGD算法更新整个网络的权值矩阵，经过不断迭代训练，直至误差收敛[16]，模型训练框架流程图如图3所示。

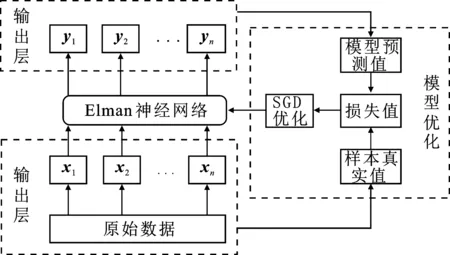
图3 燃烧室温度模型训练流程

原始输入数据经过输入层、隐含层、输出层得到模型预测值，将得到的模型预测值与真实样本值进行计算以获得损失值，并以此为依据进行模型优化。最后，在满足模型训练终止条件的情况下得到最终训练好的Elman神经网络模型用于燃烧室温度预测。

用于Elman神经网络模型训练的燃烧室温度模型的输入输出曲线如图4和图5所示，燃烧室温度模型训练集输入信号为分别在5 s以及25 s时的一个斜坡信号，总时间为140 s，采样时间为0.1 s，训练集共1 515对输入输出数据。

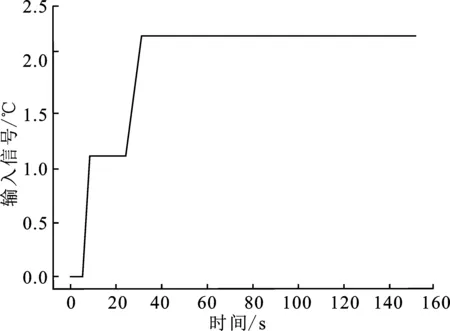
图4 燃烧室温度模型的训练集输入曲线

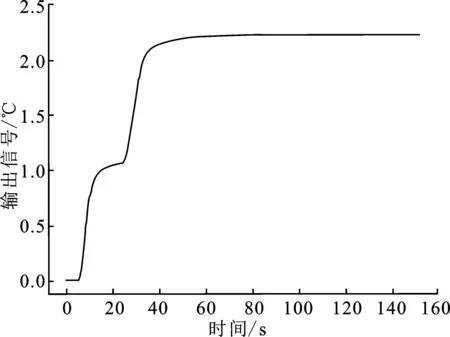
图5 燃烧室温度模型的训练集输出曲线

图6是Elman网络训练误差，由图6可以看出，模型训练至200次左右时已基本收敛，网络训练的损失值约为0.000 4 ℃，模型训练误差非常小，模型精度较高。

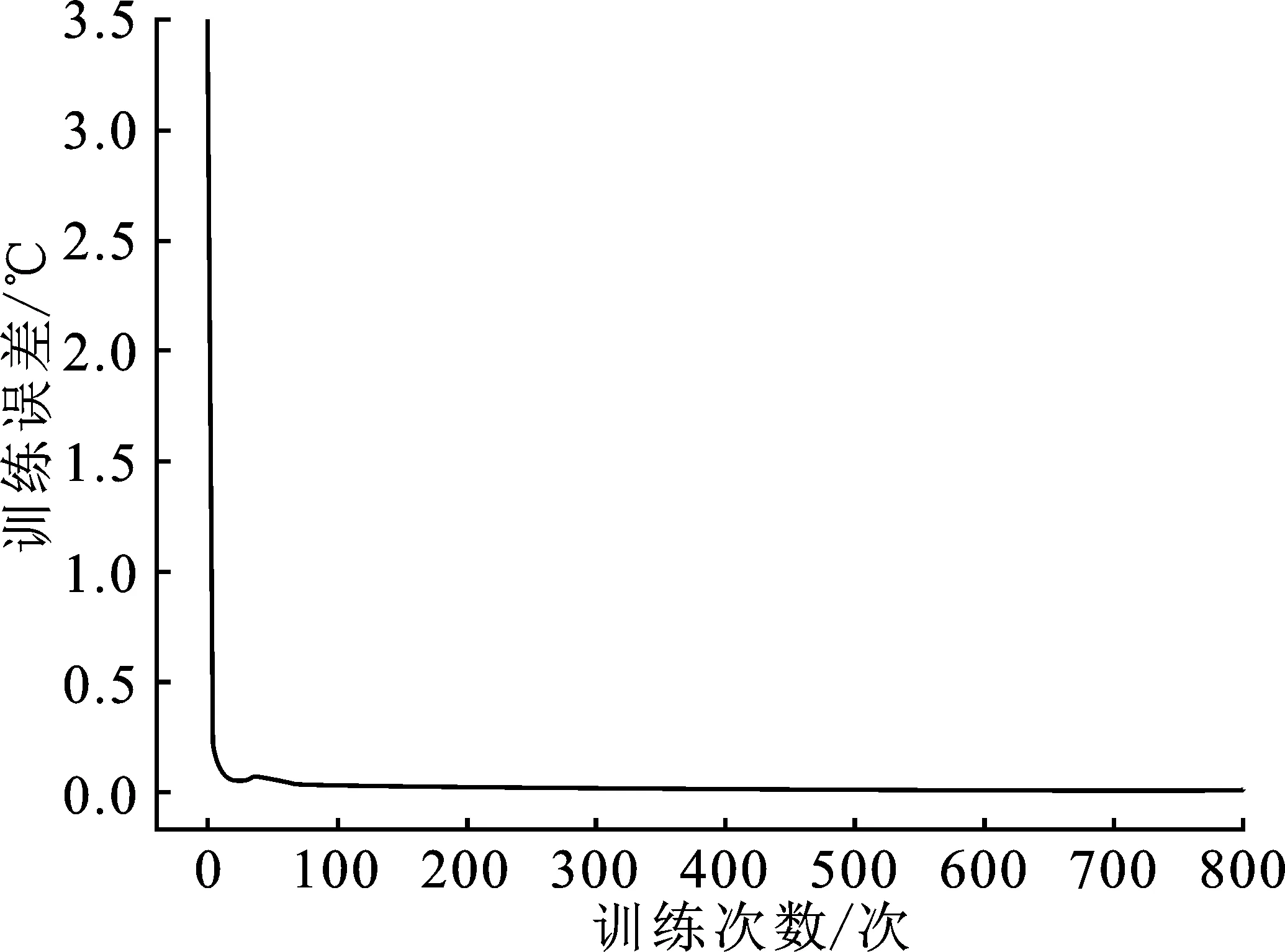
图6 Elman神经网络训练误差曲线

ITAE(Integral Time Absolute Error)性能指标是控制系统的一种常用性能评价指标。如式(22)所示，ITAE的实用性和选择性都比较好。对于离散系统来说，其ITAE性能指标如式(23)所示。

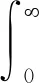
(22)

(23)

式中，T为采样周期；i为采样时刻。选取离散系统ITAE性能指标作为燃烧器温度模型的性能评价。

用于测试Elman神经网络燃烧室温度模型的输入信号为单位阶跃信号及单位斜坡信号，即对温度设定基准增加1 ℃。Elman神经网络温度模型输出响应曲线以及原温度模型的响应曲线如图7和图8所示，Elman神经网络模型输出跟踪输入的误差以及ITAE指标如表1所示。

表1 Elman神经网络模型与原模型ITAE指标比较

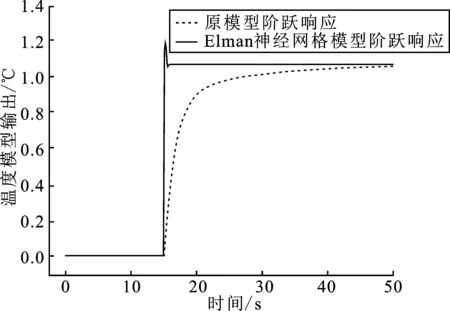
图7 Elman神经网络模型阶跃响应曲线

结果表明，利用Elman神经网络建立的燃烧室模型对阶跃输入及斜坡输入的动态跟踪效果良好，Elman神经网络模型的ITAE指标均优于原模型，分别为16.103 4、8.990 1。统计得到，Elman神经网络燃烧室温度模型跟踪输入的平均误差为0.000 4，误差精度可达0.04%，且建立的Elman神经网络温度模型稳态误差误差较低，精度更高，仅在温度阶跃增加及斜坡输入变化时存在超调。

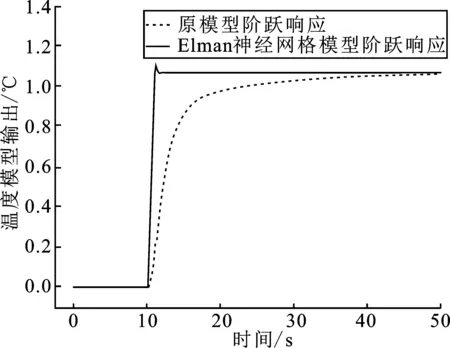
图8 Elman神经网络模型斜坡响应曲线

5 结束语

本文针对燃烧室温度模型具有非线性、强耦合的特点，建立了燃烧室温度的Elman神经网络模型，采用了BPTT算法以及SGD算法进行网络误差的传播和权值更新。仿真结果表明，所构建的燃烧室温度模型能够较好地预测燃烧室温度，其响应速度以及预测误差均优于传递函数模型。证明了本文所提基于Elman神经网络燃烧室温度模型具有一定的可靠性和稳定性，为燃气-蒸汽联合循环发电机组的其他部分建模提供了参考。