基于模态分析的海洋立管运动监测装置优化布置

张振兴，隋鸿冰，刘军鹏*

（1.海洋石油工程股份有限公司，天津 300450；2.中国石油大学（北京）安全与海洋工程学院，北京 102200）

立管是海洋平台结构与海底装置的主要连接件，是海洋油气生产系统的重要组成部分。在复杂的工程环境下，由于浮体运动、立管自重和管土作用等因素、立管容易在端部和触底点区域发生失效，需要在设计时重点关注。此外，在海流作用下，立管作为一种细长杆件，因涡激振动容易发生疲劳损伤。一旦海洋立管出现疲劳损伤和破坏，不仅会对海洋石油生产系统造成影响，而且还会对国家造成严重经济损失甚至造成海洋生态系统的破坏。利用运动监测装置对立管进行健康状态监测是保障生产可靠性的一种手段，受经济、立管所处环境等多种因素的制约，安装在立管上的监测装置数量是有限的。如何使用最少数量监测装置将其合理布置在海洋立管上，并获取近似真实的监测信息便成为海洋立管运动监测装置优化布置最重要的问题[1-2]。

近年来，基于结构模态分析的运动监测装置优化布置方法已经被广泛应用于土木工程结构的健康监测中，王秀丽等[3]通过对管桁架罩棚结构进行模态分析来了解动态响应，确定了监测装置布置的最优方案。NATARAJAN S等[4]发展了基于模态分析的监测装置优化布置方法，提出了配置清晰度指数（Configuration Clarity Index）的概念，并通过使用此种方法对海洋立管进行了监测装置的优化布置。阴宏宇[5]根据有效独立法进行监测装置布点的初选之后，使用模态置信度矩阵法（Modal Assurance Criteria，MAC）进行了海洋立管监测装置布点位置的优化。刘义勇等[6]从模态正交性和参数识别敏感性出发，综合选取了模态置信度矩阵和Fisher矩阵作为评估标准对顶部张紧式立管进行了监测装置布点优化，相对于传统算法提高了收敛精度、收敛速度以及寻优能力。

结构模态参数的改变可以作为结构早期疲劳损伤的标志，成为振动方法进行损伤诊断的切入点，因此，基于结构振动模态分析的损伤诊断法得到了广泛的应用[7]。模态分析在结构的损伤识别中是最基础、最关键的步骤，也同时结合了结构动力学、参数识别、信号采集与分析、振动测试技术等多种技术，是目前学术界普遍认可的一种方法[8]。通过对国内外监测装置优化布置的分析，模态分析在海洋立管运动监测装置的优化布置中是可行的。但是，目前对海洋立管的模态分析进行运动监测装置优化布置的研究中，大部分的研究成果仅进行了单纯的模态分析，并未考虑海洋立管工作状态下的真实海洋环境情况。孙传栋等[9]在使用ABAQUS软件对深水立管进行模态分析时，考虑了立管顶部张紧力对其的影响；刘栋梁等[10]通过使用ABAQUS对海洋立管进行了有限元分析，考虑了波浪和海流的情况，并分析了不同张紧力对立管各阶模态的影响。

不同的优化方法和准则都有着一定的内在联系，却也有着各自的特点，从而根据不同方法以及标准得到的监测装置布点方案可能相差很大。有效独立法、能量法等常用的监测装置布置优化方法均为基于模态独立性的监测装置布置方法，其在一定程度上并不能满足最佳的损伤可识别性。而对于模态清晰度指数和配置清晰度指数的方法则是利用结构响应变化进行的监测装置布置优化方法，拥有更好的损伤可识别性。本文则选择了拥有更好损伤可识别性的模态清晰度指数及配置清晰度指数的方法进行监测装置的布置优化。

海洋环境是一个复杂的环境，仅仅单独考虑张紧力、波浪和海流等情况不能完全模拟真正的海洋环境。本文则考虑了立管顶部张紧力、波浪和海流载荷以及浮式平台垂直运动作用等因素，对海洋立管进行有限元模态分析，使用相关原理将NATARAJAN S等[4]提出的模态清晰度指数和配置清晰度指数进行进一步修正，并通过与海洋立管真实环境下动态响应较大位置进行综合对比，对运动监测装置的布点进行选取和优化，此外通过对立管进行监测装置安装夹具、外壳等附加质量后的模态分析确定监测装置布点方案的正确性，并通过海洋立管的实际算例来进行运动监测装置的布置优化。

1 立管模型分析

1.1 理论分析

在海洋立管的健康监测过程中，需要用到多组运动监测装置或应变监测装置采集的多组数据来预测结构响应。本文选用单一的运动监测装置测量，假设使用的监测装置数量为n，考虑的模态数为m。确定其模态范围内的模态清晰度指数，并将其缩聚为配置清晰度指数，通过配置清晰度指数的比较获得监测装置的布置方案。由于立管上的动应力可用立管的位移进行估算，因此只要获得整个立管的位移，即可使用公式估计立管的动应力从而进行立管的疲劳计算[11]。本文所使用的监测装置为运动监测装置，其监测数据为立管的加速度，需要将测得的加速度数据通过后期的计算处理来获得立管的位移数据并进行立管的健康寿命计算，且海洋立管系统的动力响应可以由一系列离散的点的位移所确定[12]。因此本文在优化布置监测装置时，可直接通过有限元分析获取立管的位移数据来进行监测装置布置计算。

NATARAJAN S等[4]在通过对立管涡激振动响应分析发现，其立管所在的墨西哥湾海域的海洋环境下的主要激励模态范围介于第2阶到第11阶之间，因此在进行模态分析时选择了前15阶模态进行研究分析[13]。通过对立管在海洋环境下的模态分析调查发现，立管在南海海洋环境下的主要激励模态范围介于第3阶到第8阶模态之间[14]，因此在本文的研究中，主要对立管的前十阶模态进行分析研究，并通过NATARAJAN S等[3]研究中的计算原理对其模态清晰度指数和配置清晰度指数的计算求解，由于其求解的主要原理为最小二乘法原理，为了减小计算误差，本文对其计算求解方式进行了一定的修正，使其更适合于本文海洋立管运动监测装置优化布置研究。

1.1.1 模态清晰度指数

模态清晰度是用来确定两个模态之间的空间混淆程度。两个模态响应之间的差异被定义为模态的清晰度。如图2所示，模态清晰度指数越小，两个模态之间越清晰，模态振型越相似。模态清晰度指数计算为监测装置在相同位置处测得的任何两个模态振型最佳拟合之差的平方和，如公式（1）所示。

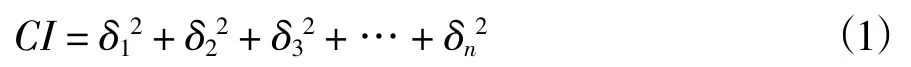
图2 模态清晰度指数

首先，构造矩阵[α]，为了提高计算精度以及加速后期求解速度，因此对矩阵中的每一列位移模态信息进行归一化处理，矩阵中每一列代表每个运动监测装置位置处的位移模态信息。各模态下的动态响应情况均可在矩阵中表现，矩阵中的每个元素代表着立管的各阶模态下监测装置位置处的位移数据，某个位置动态响应越大，矩阵中相应元素数值也就越大。维数为n×m的矩阵[α]表示在n个监测装置位置处和m阶模态下的数值[15]。

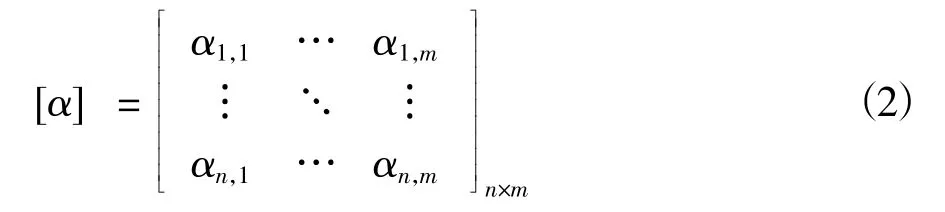
式中，αn，m为第m阶模态下第n个监测装置位置处的位移模态信息。

假设激发了第p阶模态，则可使用最小二乘法计算整个模态范围内的最佳拟合振幅，原式如公式（3）所示，通过使用最小二乘法中回归方程的方法，将最佳拟合振幅的求解公式进行的修正，第p阶模态的[α]p到第q阶模态的[α]q的最佳拟合振幅λp，q由公式（4）给出。

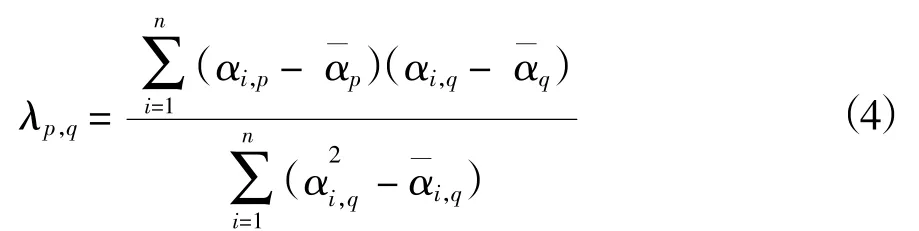
根据最小二乘法原理得到的上述公式以及模态清晰度指数的定义式，可计算得到模态清晰度指数。模态清晰度指数为激发模态p和模态q之间最佳拟合之差。具体由公式（5）所示，

式中，CI为模态清晰度指数；αp、αq为第p和第q模态下各结点的模态信息。

1.1.2 配置清晰度指数

上式求得的模态清晰度指数将通过再计算处理浓缩来表示监测装置布置的代表性指标，计算处理后的参数称之为配置清晰度指数[4]。配置清晰度指数可以简单理解为模态清晰度指数的均方根值也为有效值，其可以在不同响应模态下，计算关注的不同模态的清晰度指数。

首先，利用NATARAJAN S等[4]原文所用公式（6）求得的清晰度指数进行平均化处理，具体由下式所示。

式中，CIp为平均清晰度指数。

通过上式求得的平均清晰度指数，进一步进行不同响应模态下的模态清晰度指数计算。为了更好地适应于本文的研究对象，对不同响应模态下的模态清晰度指数的计算方式进行了简单修正，将计算模态数限制在十阶内，公式如下式。

式中，LMCI为前2阶模态的清晰度指数处理；MMCI为第3到8阶模态的清晰度指数处理；HMCI为第9到10阶模态的清晰度指数处理。

最后，将公式（7）、（8）、（9）中求得的数值带入下式，则可求得所需的配置清晰度指数。

式中，n为监测装置数量；ρl、ρm、ρh为各类模态清晰度缩聚指数考虑的比重。

1.2 立管模型建立

本文对南海流花16-2油田中的某柔性立管进行运动监测装置的布置优化，其构型示意图如图3所示。

图3 流花16-2柔性立管构型示意图

分析中所使用的流花16-2柔性立管所处海域水深400 m，全长600 m，各段长度如表1所示，由于在ABAQUS软件中无法进行固定长度的柔性立管的建模，因此首先在SolidWorks三维绘图软件中对此柔性立管进行建模，之后将模型导入ABAQUS软件中进行分析模型的建立，分析模型如图4所示。

表1 柔性立管各段具体长度 单位：m

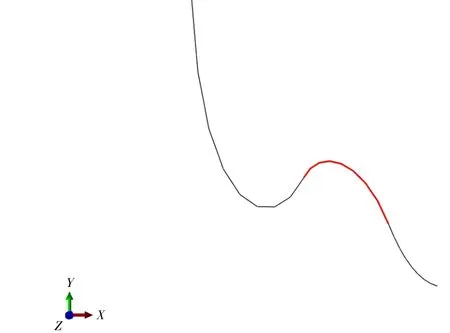
图4 ABAQUS中柔性立管二维模型（红色为浮筒段）

在ABAQUS中选用二维的B21管道结构对建立的模型进行模态分析，其结构主要的材料特性为：立管外径为0.313 94 m，壁厚为0.078 99 m。由于柔性立管有多层结构，并且已知该柔性立管的试验参数，因此在进行模态分析时的所使用的弹性模量等数据均使用柔性立管等效计算后的参数。将柔性立管等效为一层结构，如图5所示，根据圆管的弯曲刚度公式[16]计算柔性立管等效弹性模量。

图5 等效柔性立管截面图

式中，EIpipe为柔性立管的弯曲刚度；E为柔性立管的等效弹性模量；R2为柔性立管外径；R1为柔性立管内径。

通过以上的等效计算，可得到分析所需的各项参数，具体参数的数值如表2所示。

表2 柔性立管各项参数

安装有浮筒的柔性立管如图6所示，考虑到浮筒对于柔性立管的弯曲刚度有一定的影响，本文对立管进行分析时对立管浮筒段进行了单独处理。将浮筒段中浮筒和柔性立管的弯曲刚度进行等效，获得等效弯曲刚度[17]。

图6 安装浮筒的柔性立管[18]

式中，EI立管为柔性立管的弯曲刚度；EI浮筒为浮筒的弯曲刚度。

表3 浮筒基本结构参数

1.3 边界条件及载荷的设定

在ABAQUS中建模完成的柔性立管以30 m为一个单元，将其立管结构分为20个单元，包含21个结点，结点位置在图7中使用代号标出。其中，每个结点将会产生6个自由度的运动[20]，分别为X、Y、Z 3个方向的平移和X、Y、Z 3个方向的旋转。

图7 柔性立管二维模型结点示意图

在流花16-2柔性立管的21个结点中，结点1处为柔性立管与浮式平台的连接处，结点21处为柔性立管的触地点。对于柔性立管的浮筒段，冯铁成[21]在其试验中保留浮筒段的两个平移自由度，在此模拟中也将参照其试验保留浮筒段的两个自由度。因此，在进行柔性立管的模态分析时，对柔性立管模型进行边界条件的设定，结点1处和结点21处由于浮式平台和管土作用的影响，对其自由度进行了限制，参照其他相关文献，将此两结点进行简支约束[22]。将浮筒段（结点13至结点18处）仅保留两个平移自由度，完成了此边界条件的设定，即可对该模型进行完整的模态分析。为了模拟柔性立管更加真实的海洋工作环境，在进行其固有频率和振型求解时，由于浮式平台的垂直运动作用以及立管与平台的连接原因，在柔性立管的顶部设置顶部张紧力以及垂直运动位移[22]；在分析中还考虑波浪和海流的作用，在此将其设置为均匀流场[23]，在考虑柔性立管所承受的波浪和海流作用时，本文对柔性立管所承受的拖曳力和惯性力作用进行了设置。所有边界条件和外部载荷的设定，更为真实地模拟了海洋立管的工作环境，具体设置参数由表4所示。

表4 具体设置参数

在对上述条件进行设置和分析后，通过对分析得到的数据进行MATLAB处理计算，即可得到监测装置的布置方式及布点位置。为了保证得到的布点位置能够满足实际工程环境下使用监测装置夹具、外壳等较重设备进行安装监测并获得全面的监测信息。由于监测装置夹具、外壳等质量较大，对立管的动态响应有着一定影响，因此，本文在得到监测装置的布置方式后，对柔性立管安装监测装置位置处进行附加质量设置，单点质量为50 kg，并进行整体模态分析。

2 结果分析

2.1 ABAQUS有限元结果分析

在对海洋立管的模态分析中，由于只有低阶模态对响应有显著影响[24]，因此本文将前10阶模态作为重点的研究模态[25]，以验证上文中所述理论分析的适用性。

通过对流花16-2柔性立管的模态分析，可得到结构的前十阶模态振型，其中前六阶模态振型如图8所示。在柔性立管的服役期间，浮式平台与立管连接区域（结点6、7处附近）、浮筒段（结点13、14处附近）以及触地区域（结点19、20处附近）的疲劳损伤较大[26]，应为柔性立管健康生命周期监测的重点监测位置，因此在布置时，要保证这三处位置附近有监测装置放置。

图8 柔性立管结构前六阶模态振型

2.2 理论结果分析

通过对柔性立管的前10阶模态进行有限元分析，得到了柔性立管上21个结点处的位移数据，选取总位移数据带入本文第1节中的理论分析中进行计算。由于在ABAQUS有限元软件的模态分析中，本文只选取了前10阶模态，通过对柔性立管在南海海洋环境下的主要激励模态分析，经过其模态分析后所得到的每阶模态的有效质量进行计算，本文所取各模态下的考虑权重ρl为0.36，ρm为0.54，ρh为0.1。

本文的计算实例均使用单一的运动监测装置，布置的目标是使用尽可能少的监测装置来获得最真实和最全面的海洋立管的健康寿命数据。假设除柔性立管最顶端的1号结点和最底端的21号结点之外，其余19个结点均放置监测装置，通过对上一节中的公式计算，将得到一个均布配置清晰度指数（CCI），即均布监测装置时的有效值，数值为7.922。将计算得到的均布配置清晰度指数作为一个标准，与后续进行的选择多组不同数量不同布点位置的监测装置分析所求得的配置清晰度指数进行比较。若在不同位置放置监测装置的配置清晰度指数大于均布配置清晰度指数，即超过有效值，便可认为此种监测装置布置方法可行。但是通过有限元模态分析结果得到的动态响应较大位置（浮式平台连接处、浮筒段、触地区域）均需布置监测装置，因此，在进行布置及位置结点选择时，需要包含这三个区域的结点。

通过上述方法对流花16-2柔性立管进行监测装置的优化布置，对布置数量进行分析，发现选择3个、4个、5个监测装置布置方法时，均不符合布置的要求。当从19个结点中选择6个结点进行监测装置布置时，共有27 132种布置方法。

当选取6个结点布置监测装置时的各种布置方法计算所得到的配置清晰度指数大于均布配置清晰度指数的布置方案有565种，如图9所示，但是满足动态响应较大位置布置监测装置要求的布置方法仅有一种情况，布点位置如表5所示。因此，在流花16-2柔性立管的监测装置布置中，使用监测装置数量最少为6个。虽然此种布置方案满足了布置要求，但是为了获取更加全面的柔性立管监测数据，本文选择了7结点进行监测装置布置方式。

图9 选用6结点监测装置布置方式

表5 6结点监测装置布置方式

当从19个结点中选择7个结点进行监测装置布置时，共有50 388种组合布置方法。分别计算求得这些布置方法的配置清晰度指数并与均布配置清晰度指数对比，共有483种情况符合配置清晰度指数的对比要求，如图10所示。但是满足动态响应较大位置布置监测装置要求的布置方法仅有6种情况，布点位置如表6所示。

图1 安装有监测装置的海洋立管

表6 7结点监测装置布置方式

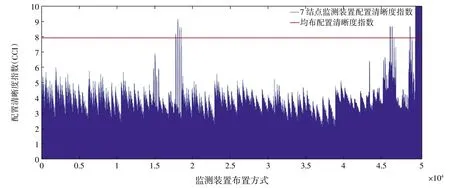
图10 选用7结点监测装置布置方式

最终，选取6种布置方式中的第一种情况，此种布置方式的配清晰度指数的最大，表明与其他情况布置不同的监测装置布置处的动态响应相对来说较大，能够对柔性立管进行更好的监测。

为了更加准确的监测流花16-2柔性立管触地区域和浮式平台连接区域的健康寿命，通过对此立管的计算分析和有限元模拟分析，可以选取获得监测信息更加完善、更加详细的监测装置布置方式。因此，对于流花16-2柔性立管的生命健康周期监测来说，选取7个结点进行监测装置的优化布置将更为有效。

2.3 立管附加质量结果分析

经过上述理论结果分析，确定了7结点的布置方式及布点位置，为了确定布点位置的正确性以及考虑监测装置安装夹具及外壳的质量对柔性立管动态响应的影响，本文在7个监测装置布置位置处进行了附加质量设定，并再次进行模态分析，同2.1节的模态分析相比，此次模态分析后的模态振型及得到的位移数据有所不同，前六阶模态振型如图7所示。

图11 附加质量分析后柔性立管前六阶模态振型

将此次分析得到的位移信息进行处理，得到了附加质量后的均布配置清晰度指数，其值为7.912 6。将此均布配置清晰度指数作为一个标准，并从19个结点中选择7个结点进行监测装置布点分析计算。其中，7结点布置方式如上节计算相同，共有50 388种布置方式，计算求得这些布置方法的配置清晰度指数并与均布配置清晰度指数对比，共有485种情况符合要求，如图12所示。但是满足动态响应较大位置布置监测装置要求的布置方法有9种情况，布点位置如表7所示。

表7 附加质量分析后7结点监测装置布置方式

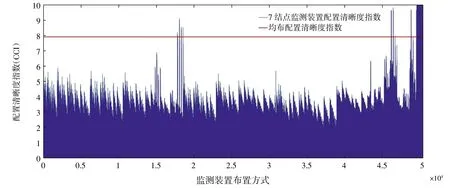
图12 附加质量分析后选用7结点监测装置布置方式

通过对附加质量后的7结点监测装置布置方式的分析，可以发现，得到的9种监测装置布置方式中，前6种与未进行附加质量分析得到的7结点监测装置布置方式相同，且第一种布置方式即为附加质量分析时所使用的监测装置布点位置。因此，可以确定监测装置夹具及外壳的附加质量对于柔性立管整体影响相对较小。

为了验证此种监测装置布置优化的正确性，本文引入模态置信度矩阵（MAC矩阵）方法进行验证，模态置信度矩阵可表示为：

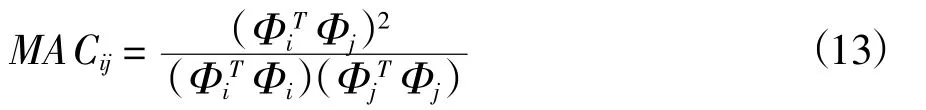
式中，Φi、Φj分别为结构的第i阶和第j阶模态振型向量。

首先，通过上述公式，计算初步测点的MAC矩阵，提取矩阵中非对角元素的最大值；然后，增加一个待测点，重新计算MAC矩阵并提取非对角元素最大值；重复相同操作，直至所有测点都加入布点方案，然后对所有非对角元素最大值进行比较，当数值最小时，此布置方案则为最优。

本文通过模态清晰度指数及配置清晰度指数的方法，求得6个监测装置即可完成柔性立管的动态响应监测，因此，将6个监测装置的布置方式作为初步的布点方案，不断增加测点，直至遍历监测装置数目，进行MAC矩阵的计算，并进行非对角元素最大值比较，MAC矩阵非对角元素最大值变化情况如图13所示。

图13 MAC矩阵非对角元素最大值变化情况

通过对非对角元素最大值比较可以发现，在遍历监测装置数目（19个）时，非对角元素最小，但此种监测方案严重增大了监测成本，因此，7个监测装置的监测方案则成了布置的最优选择，此种监测装置布置方案正与本文方法所求得的7结点监测装置布置优化方案相对应。

通过使用MAC矩阵的评价准则结果分析，可以得到7结点监测装置布置方案是本文对南海流花16-2油田中的某柔性立管进行运动监测装置的布置优化的最佳方案，其最终监测装置布置方式如图14所示。此布置方式中能够较为全面的监测柔性立管各种情况下的动态响应，可作为工程实际中的监测装置布置方式。

图14 监测装置最终布置方式

3 结 论

为了满足海洋立管的生命健康周期监测的要求，本文使用了基于模态分析的监测装置优化布置方法，使用了NATARAJAN S等[4]提出的模态清晰度法和配置清晰度法并通过相关原理对模态清晰度指数和配置清晰度指数的计算方式进行了进一步的修正，对海洋立管的监测装置优化布置及使用监测装置的最小数量进行了分析和计算。

通过对流花16-某柔性立管的ABAQUS分析以及基于模态清晰度法和配置清晰度法的理论分析，对选取6个、7个监测装置布置进行了讨论，确定了此立管最少可使用6个监测装置进行监测。考虑到立管各区域的健康监测和海洋工程监测系统的监测成本和立管自身的工作性能，并以此完善了监测装置的优化布置，最终选取了更为有效的7结点布置方式。此外，本文通过对立管进行附加质量的模态分析，确定了此种监测装置布置方式的正确性。

此种方法能够很好地对立管监测装置进行优化布置，并使其获得较为完善的立管数据，验证了模态分析法对于海洋立管监测装置优化布置的适应性。此方法对于海洋工程健康监测领域有着重要的意义，不仅可以应用在海洋工程领域，对于其他领域的监测装置优化布置也可提供一定的参考。