GPS卫星信号测量波浪技术研究

齐占辉，李明兵*，邓卓雅，于建清

（1.国家海洋技术中心，天津 300112；2.国家海洋标准计量中心，天津 300112）

海洋观测技术对我国的海洋科技进步和海洋安全保障等具有重要的意义。海浪是最重要的海洋环境要素之一，在我国历年发布的海洋灾害公报中，海浪灾害在各种海洋灾害中造成的人员死亡失踪和经济损失都高居第2位。在2020年的《中国海洋灾害公报》[1]中，海浪灾害共造成0.22亿元的直接经济损失，死亡或失踪共有6人。因此，加强海浪的精细化监测和精细化预报对人民生命财产安全、经济建设、海洋灾害预防和海上船舶运输等都有非常重要的作用和意义。波浪浮标是应用最广泛的波浪观测设备，它采用球形体的外形结构，具有良好的随波浪运动的特性，它能够模拟波浪水粒子的圆周运动，现场通过观测浮标的运动数据，就可以解算出波向、波周期以及波高等海浪信息[2-4]。波浪浮标使用简单方便、测量精度高，不受一些海洋环境限制，使得波浪浮标在海浪测量中得到了大规模的应用，使其成为最常用的海浪观测仪器之一。海浪灾害会对沿海地区人民的生命财产安全造成巨大的危害，同时也会对沿海地区繁荣的经济造成巨大的损失，因此需加强波浪的精细化监测和精细化预报，根据观测的当前波浪数据大小以及预报的未来波浪数据大小，及时采取措施疏散沿岸人民群众，加固沿岸防波浪冲击破坏的堤坝等水工建筑物，保护沿岸人民群众的生命财产安全，保障沿岸经济的繁荣快速发展，从而进一步提高沿岸地区抵御波浪灾害的能力。

目前，传统上的波浪浮标是利用重力加速度的原理来测量波浪，它在浮标体里放置加速度传感器、陀螺仪传感器和方位传感器等来获取浮标的运动数据，进而计算出波周期、波高和波向等海浪的特征参数。重力加速度型的波浪浮标在我国非常多的海洋观测点都得到了应用，取得了非常好的波浪观测效果。在国外，成熟的重力加速度型波浪浮标产品主要有荷兰的Datawell波浪骑士测波浮标[5]和加拿大的Triaxys波浪浮标[6]。特别是很多波浪观测仪器在现场海上比测时都把波浪骑士测波浮标观测到的波浪数据作为标准的波浪数据源[7-10]。在国内，广泛应用的重力加速度型波浪浮标产品主要有国家海洋技术中心的SBF6-1型波浪浮标、山东省科学院海洋仪器仪表研究所的SBF3型波浪浮标[11-12]和中国海洋大学的SZF型波浪浮标[13-14]等。中国科学院南海海洋研究所研制的波浪传感器也采用重力加速度的测量原理，其采用捷联姿态补偿方法替代传统机械常平架，使波浪传感器的体积、功耗、造价等均有下降。以上几款重力加速度型波浪浮标产品的技术状态非常成熟，为我国波浪观测事业做出了巨大的贡献。

近几年，全球卫星导航系统在我国海洋领域的应用越来越广泛，深入到了海洋领域中的方方面面。目前，国内外提出了一种利用卫星信号来测量波浪的技术，即卫星测波浮标，它不同于传统上重力加速度的测量原理。卫星测波浮标只需要在浮标体内安装一个卫星信号接收机，不需要再安装额外的传感器就可以测量波浪。卫星测波浮标只要能够接收到卫星信号，就可以测量波浪。目前，国内外多家科研机构都进行了卫星测波技术的研究，并且取得了一些研究成果。荷兰、英国、日本等国家的科研机构对GPS（Global Positioning System）卫星测量波浪进行了研究。特别是荷兰的Datawell公司已经批量生产和销售了DWR-G4、DWR-G7和DWR-G9等3种型号的GPS卫星测波浮标产品[5]，如图1所示。在2003年，荷兰的Datawell公司在澳大利亚布里斯班黄金海岸对GPS卫星测波浮标和传统的重力加速度型测波浮标进行了海上现场比测试验，比测结果如表1所示[15]。从比测结果可以看出，观测到的两组波浪数据很一致。英国也进行了GPS卫星信号测量波浪的研究，其研制的GPS卫星测波浮标在太平洋东海岸和荷兰Datawell公司的重力加速度型波浪浮标进行了海上现场比测试验，如图2所示，两者的数据结果也非常一致[16]。日本也进行了GPS卫星测量波浪的研究，在纪淡海峡，做了一个月的GPS卫星波浪传感器和重力加速度型波浪传感器的海上现场比测试验，从数据的比测结果看，两者测量的波浪参数非常一致，波高误差在10 cm以内，波向误差在5°以内[17]。在国内，国家海洋技术中心、山东科技大学、国家海洋标准计量中心、天津大学等都进行了GPS卫星测量波浪技术的研究，并且都取得了一定的研究成果[18-22]。特别是国家海洋技术中心在2011年就开始了GPS卫星测量波浪的研究工作，逐步解决了GPS卫星测量波浪的关键问题，研制成功了GPS卫星测波浮标，在图3中展示了其实物图、结构组成示意图及硬件组成示意图。在图3中，海面水线在浮标体的中间位置，GPS天线在浮标体的顶部，距离海面有一定的距离，GPS天线能够接收到卫星信号。国家海洋技术中心的GPS卫星测波浮标已经在自然资源部得到了应用，获得了很好的应用效果。同时，国家海洋技术中心在印度洋、西太平洋以及南极西风带等海域布放了若干套GPS卫星测波浮标，浮标在经历了多次台风大浪过程后各部分功能均工作正常稳定。

图1 荷兰Datawell海洋仪器公司的GPS卫星测波浮标[5]

图2 英国的GPS卫星测波浮标与重力加速度型测波浮标的海上现场比测结果[16]

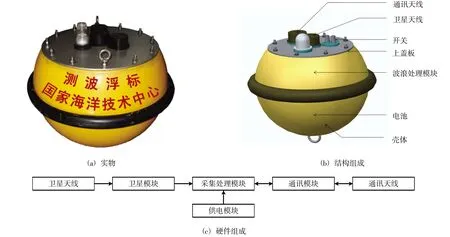
图3 国家海洋技术中心研制的GPS卫星测波浮标

表1 两类测波浮标测得的波浪参数的相关系数[15]

1 卫星信号测量波浪技术原理

卫星信号测量波浪主要是利用卫星导航定位信号的多普勒频移值计算出浮标的运动速度数据，然后由运动速度数据根据海浪理论解算出波向、波周期以及波高等海浪信息。目前，美国的GPS卫星导航定位系统最成熟，导航定位精度最高。因此，以美国的GPS卫星导航系统为例，如图4所示为GPS卫星导航定位信号测量波浪的工作原理示意图及测量算法流程图。GPS卫星测波浮标在海面上随着波浪的运动一起起伏和摇摆，浮标中的GPS接收机从各个方向上的GPS卫星导航系统接收GPS卫星信号。由多普勒频移原理得知，GPS卫星测波浮标和GPS卫星系统两者之间存在有相对运动，使得GPS卫星系统发射的卫星信号载波频率和GPS卫星测波浮标中的GPS接收机收到的卫星信号载波频率是不一样的，它们之间的频率差值称为多普勒频移。它和卫星测波浮标的运动速度、运动位置等运动状态信息都有关系。利用多普勒频移计算出浮标的运动速度，然后再根据运动速度就可以解算出波向、波周期和波高等海浪信息。

图4 GPS卫星导航定位信号波浪测量原理和测量算法流程的示意图

GPS接收机运动速度的获取是GPS卫星测波技术的一个关键核心问题。在美国的GPS卫星信号干扰措施取消之后，利用多普勒频移值计算运动速度的精度能够达到厘米/秒的量级，更高能够达到毫米/秒的量级[23-26]。所以，由多普勒频移值计算出的速度数据能够满足波浪测量的精度要求。

设GPS接收机在t时刻与第i颗GPS卫星的伪距为ρi，如下所示：

在公式（1）中，c表示光速；（xi，yi，zi）表示第i颗GPS卫星的坐标位置，由星历导航电文能够计算得到，是已知量；Δt表示GPS接收机与GPS卫星导航定位系统之间的时钟钟差，是未知量；（x，y，z）表示GPS接收机计算输出来的坐标位置，是已知量。第i颗GPS卫星在t时刻发射的卫星载波信号频率为fi，卫星测波浮标中的GPS接收机接收到的卫星载波信号频率为fri，两者之间的多普勒频移值为：

GPS接收机与GPS卫星导航定位系统的伪距变化率ρi′和多普勒频移值dfri的大小有关，计算公式如下。

其中，GPS卫星信号的多普勒频移值dfri根据GPS接收机的原始频率观测值得到。因此，由公式（3）能够计算出伪距变化率ρi′。由公式（1）求导得：

在公式（4）中，（xi′，yi′，zi′）是第i颗GPS卫星在t时刻的运动速度，根据星历表能够直接查出，是已知量；（x′，y′，z′）是GPS接收机在t时刻的运动速度，是未知量；Δt′是GPS接收机相对于GPS卫星导航系统的时钟钟差变化率，也是未知量。公式（4）中有x′、y′、z′、Δt′共4个未知变量，因此，GPS卫星测波浮标中的GPS接收机需要同时接收到4颗或者4颗以上的GPS卫星导航定位信号才能求解出这4个未知变量。把公式（4）修改为：

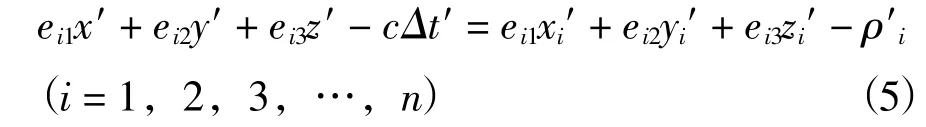
当GPS接收机接收到4颗GPS卫星信号时，即n=4时，则4个未知变量求解为X=A-1L。当GPS接收机接收到4颗以上的GPS卫星信号时，即n＞4时，则4个未知变量求解为X=（ATA）-1ATL。

综上所述，根据GPS卫星导航定位信号就可以解算出浮标的运动速度（x′，y′，z′）。

海浪具有无规律的随机运动特征，因此，通常用随机过程的概率理论来分析和研究海浪。GPS卫星测波浮标在海上现场观测时，对其计算出的浮标运动速度分量z′进行一次时域数值积分并带通滤波后求得海面的位移变化序列，然后利用跨零点法计算出一段时间内海面从大到小排列的波高序列H1、H2、H3、H4…Hn-1、Hn，以及对应的波周期序列T1、T2、T3、T4…Tn-1、Tn。则波高和波周期的特征值计算公式如下。海面瞬时点的波向值θ是由计算出的浮标两个瞬时运动速度分量x′、y′的比值求出，对所有瞬时点的波向值θ进行统计分析，找出出现概率最大的波向值，即为这段时间内波浪的表观主波向。

2 实验室校准试验

国家海洋标准计量中心是我国波浪观测仪器校准检定的第三方专业机构，拥有多种类型的波浪检测装置。在国家海洋标准计量中心对GPS卫星波浪传感器进行了校准试验，评估其波高和波周期的测量精度。试验时把GPS卫星波浪传感器安装固定在波浪校准检定装置的顶端，随波浪校准检定装置一起做圆周运动，模拟波浪水粒子的圆周运动。波浪校准检定装置的旋转直径（1.98 m）用于模拟波浪的高度，旋转周期用于模拟波浪的周期。在试验时，把波浪校准检定装置放置在室外空旷无遮挡且卫星信号接收良好的场所。同时，波浪校准检定装置的结构简单，并不会影响卫星信号的接收。

如表2所示为GPS卫星波浪传感器的实验室校准试验数据结果。在7次试验中，波高的标准值均为1.98 m，波周期的标准值分别为3.8 s、5.0 s、6.3 s、8.4 s、11.1 s、12.4 s、25.0 s。在7次试验的结果中，波周期的最小误差为0.00 s，最大误差为0.16 s，平均误差为0.077 1 s。在校准前，波高的最小误差为0.00 m，最大误差为0.28 m，平均误差为0.138 6 m。对7次试验中的波浪标准值与校准前波高测量值的比值进行平均化处理，得到平均校准系数为0.938 4，写入GPS卫星波浪传感器的配置参数中，进而得到校准后的波高值。在校准后，波高的最小误差为0.00 m，最大误差为0.14 m，平均误差为0.082 9 m，其波高测量精度得到了进一步的提高，达到了实验室校准的目的。

表2 实验室试验数据结果

3 海上比测试验

除了在实验室进行校准试验外，在山东省青岛市近海海域也进行了GPS卫星测波浮标和重力加速度型波浪骑士测波浮标的海上现场比测试验，试验海域水深约为25 m，两套波浪浮标布放距离相距约为0.5 km。在两套测波浮标进行海上数据结果比较时，按照每小时采集一组原始波浪数据，每组数据统计时长约为17.07 min。

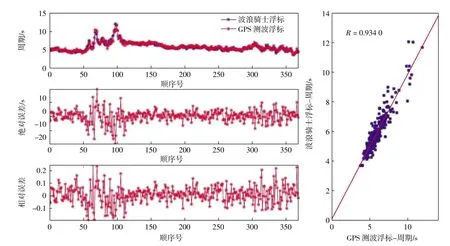
图6 有效周期的数据比较

两套波浪浮标的海上现场比测结果如图5至图7和表3所示。比测时，两套波浪浮标的波高、波周期数据均是通过时域跨零点法计算得到的；卫星测波浮标的波向是通过本文的时域波向统计方法计算得到的，波浪骑士测波浮标的波向是通过波浪谱方法计算得到的。从比测结果中可以看出，两套波浪浮标在本次试验中测量的波周期、波向以及波高的数据变化曲线很一致。波高的相关系数为0.981 6，测量误差大部分在10 cm以内，平均误差为5.24 cm，最小误差为0.01 cm，标准偏差为4.53 cm。波周期的相关系数为0.934 0，测量误差大部分在1 s之内，平均误差为0.31 s，最小误差为0.00 s，标准偏差为0.31 s。波向的相关系数为0.364 0，测量误差大部分在20°之内，平均误差为13.31°，最小误差为0.00°，标准偏差为10.07°。虽然在本次试验中，两组波向数据很一致，但是波向的相关系数较波高和波周期的相关系数低，经分析主要是由于在本次比测期间，该海域的波向值变化趋势不是很大，从而造成波向的相关系数较低，但从数据误差角度分析，两套波浪浮标测量的波向数据也是非常一致的。

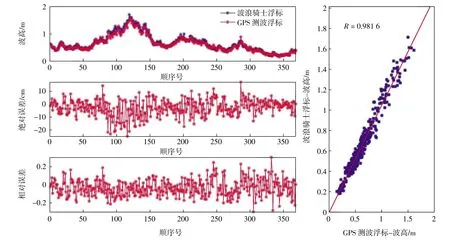
图5 有效波高的数据比较

表3 GPS测波浮标与波浪骑士浮标的波高、波周期和波向的数据比测结果

图7 波向的数据比较

4 结 论

不同于传统上重力加速度型波浪浮标的波浪测量原理，本文详细给出了一种利用GPS卫星导航定位信号测量波浪的技术工作原理。为了验证这一技术工作原理，首先利用国家海洋标准计量中心的波浪校准检定装置进行了实验室模拟测量波浪试验，其波高的平均测量误差为8.29 cm，波周期的平均测量误差为0.077 1 s。然后，在山东省青岛市近海海域进行了GPS卫星测波浮标和波浪骑士测波浮标的海上现场比测试验，从试验结果可以看出，波高的平均误差为5.24 cm，波周期的平均误差为0.31 s，波向的平均误差为13.31°。综上，通过实验室校准试验和海上现场比测试验的结果均验证了本文提出的GPS卫星导航定位信号测量波浪技术工作原理的有效性以及可行性，其波高、波周期和波向的测量精度能够满足波浪测量的精度要求，与传统的重力加速度型波浪浮标的测量精度在同一等级上。传统的重力加速度型波浪浮标由于借助于方位传感器测量波向，因此，周围磁场环境会一定程度上影响波向的测量精度；同样，卫星测波浮标由于借助于卫星信号测量波浪，因此，卫星信号被遮挡也会影响它的测量精度。总之，两种类型的波浪浮标互为补充，共同为我国的海浪观测事业服务。

目前，本文的卫星测波浮标使用的是美国的GPS卫星信号来测量波浪，随着各国卫星导航系统的建造以及完善，特别是我国的北斗卫星导航系统的建造完成和导航定位测量精度的进一步提高，该技术将来可以应用到我国的北斗卫星导航系统进行安全可靠的波浪测量，进一步提高我国的波浪观测技术水平。