硬化土本构模型在砂土海上风电大直径单桩基础的应用

潘珂珂，翟恩地，许成顺，孙毅龙

（1.北京工业大学城市建设学部，北京 100124；2.新疆金风科技股份有限公司，北京 100176）

在海上风电单桩基础承载力计算中，p-y曲线法是工程中常用的一种计算方法，然而该方法是基于是小直径桩模型试验得来的，仅适用于小直径柔性桩[1]。国内外学者大量研究表明p-y曲线法应用于大直径单桩基础承载力计算存在巨大缺陷，p-y曲线法高估了初始地基刚度，并低估了极限土抗力[2-5]。而数值有限元法不受场地约束，是一种有效的考虑桩土作用的大直径单桩基础承载力计算方法。

在有限元法中，选取合理的本构模型是确保计算结果准确的重要因素。2012年，姚仰平等[6]研究了常用岩土本构模型对土的力学特性的反映。2016年，黄茂松等[7]总结了常用本构模型对砂土、饱和黏土及粗粒土的适用性。曾树平[8]分别建立了API规范方法、旋转硬化本构模型和Drucker Prager模型下静载水平受荷桩三维模型，结果表明旋转硬化本构模型和Drucker-Prager模型计算结果与试验结果较吻合。AHMED S S等[9]通过离心试验建立了摩尔—库伦（Mohr-Coulomb，MC）模型和修正剑桥模型下单桩基础在砂土中水平受荷的三维模型，结果表明修正剑桥模型比MC模型更能模拟试验桩体的水平变形。顾栋辉[10]在2017年研究了采用MC模型和修正剑桥模型等本构模型下单桩基础在波浪作用下的动力响应。董士欣等[11]利用PLAXIS 2D软件研究了线弹性模型、MC模型、硬化土（Hard-Soil，HS）模型和小应变硬化土模型的阻尼特性，以及其特性对计算结果的影响。2020年，潘兵等[12]基于室内模型试验，对比p-y曲线法、MC模型和HS模型的计算结果，结果表明MC模型会高估土体的水平向抗变形能力。由上述研究可知，MC模型作为较为粗略的本构模型并不能较好地描述土体在破坏之前的变形行为，而HS模型由于可以同时考虑了土体剪切硬化和压缩硬化等优点，能够较好地描述砂土等土体的水平变形行为。

综上所述，不同的计算方法应用于海上风电基础承载设计存在着差异性。因此本文基于PLAXIS 3D有限元计算平台，建立了MC模型、HS模型下的海上风电大直径单桩基础数值模型，开展了一系列数值模拟计算，并与p-y曲线法计算结果、桩土分析（PileSoil Analysis，PISA）项目[13]场地模型试验结果对比，定量分析了p-y曲线法、MC模型和HS模型3种计算方法应用于大直径单桩基础承载计算的差异性，并开展了关键因素对砂土大直径单桩基础的水平极限承载力影响规律分析。

1 计算模型及参数

1.1 砂土的p-y曲线法

海上风电单桩基础在水平荷载的作用下，桩周土体会产生塑性变形，为了较好地反映土体的塑性非线性变形特性，工程中常采用p-y曲线法来反映桩周土体的变形特性，其骨干曲线如下：

式中，A为短期荷载和循环荷载下的修正系数（循环荷载下A=0.9，静力荷载下pu为深度H处的极限承载力（浅层土下pus=（C1H+C2D）γH；深层土下pud=C3DγH。其中C1、C2、C3为随内摩擦角变化的系数；D为桩径；γ为土体的有效重度）；k为初始地基模量常数；H为深度。

1.2 MC模型

MC模型是一种理想的弹塑性模型，它基于虎克定律和MohrCoulomb破坏准则而建立。MC模型主要参数见表1。相关模型参数可以现场土工试验得到，使用简单方便，该模型在岩土工程研究中得到广泛的应用。

表1 MC模型参数表

1.3 HS模型

HS模型是一种考虑土体剪切硬化和压缩硬化的弹塑性土体本构模型，HS模型主要参数见表2。该模型基于MC模型，引入了土体剪切应力—轴应变双曲线函数关系，同时考虑了屈服面随塑性应变的增加而扩张。因而该模型可以较好地反映土体的压硬性、剪切硬化等特性。

表2 HS模型参数表参

2 数值模型计算和分析

本节基于PLAXIS3D有限元平台，参照PISA项目[13]桩基模型试验参数，建立海上风电大直径单桩有限元模型，开展了一系列数值有限元计算，将计算结果和试验结果进行对比分析，探讨p-y曲线法、MC模型、HS模型3种计算方法的差异性。

2.1 三维数值模型的建立

PISA项目是由牛津大学、伦敦帝国学院和都柏林大学等多个大学联合进行的桩基受力研究项目，其中该项目在法国Dunkirk进行了单桩基础的原型实地试验研究，水平荷载施加在桩顶位置，桩体直径分为0.273 m、0.762 m、2 m。下面基于PISA项目[13]DL2桩体试验数据建立单桩数值模型。DL2单桩基础为直径2 m的钢管桩，弹性模量为210 GPa，密度为7 850 kg/m3，钢管桩壁厚38 mm，基础埋深为10.57 m，地上部分为9.89 m，桩体采用弹性本构模拟，且桩体为实体单元。土体场地周围为绑定约束，顶部自由，桩—土相互作用采用界面单元模拟，其中界面强度折减系数根据经验取值为0.67[14]。水平荷载施加在桩体伸出泥面9.89 m处，整体模型长为20倍桩径，宽为10倍桩径，高为两倍埋深（21 m），具体三维模型如图1所示。

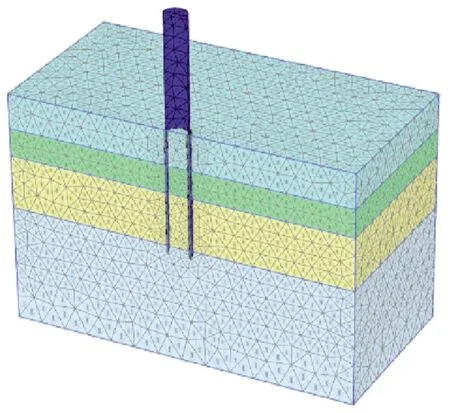
图1 有限元模型

2.2 土体参数的确定

土体为实体单元，分别采用MC模型、HS模型模拟，相应土体参数见表3和表4，MC模型和HS模型参数可以通过PISA项目[15]文献和相关经验公式[16-17]来估算，具体如下：（1）对于MC模型，主要参数有粘聚力、内摩擦角、剪胀角、弹性模量、泊松比。基于室内土工试验数据，内摩擦角选取试验数据中的内摩擦角峰值和泊松比选取0.17，其余参数按照公式进行估算。①剪胀角：其中φ′cs为32°；②弹性模量：E=2G0（1+v），其中G0通过海洋静力触探结果图得到，如图2所示[17]。（2）对于HS模型，除了以上参数以外，主要参数还有参照割线刚度、参照切线压缩刚度、参照三轴卸载/再加载刚度、刚度的应力依赖度指数、卸载/加载的泊松比、相对刚度的相对应力、正常固结的K0常数、失效折减系数，其中刚度的应力依赖度指数、卸载/加载的泊松比、相对刚度的相对应力都采用默认值，分别为0.5 kPa、0.2 kPa、100 kPa。其他参数分别按照以下公式进行估算：①参照割线刚度：=60 000RD/100，其中RD为砂土的相对密度；②参照切线压缩刚度：；③参照三轴卸载/再加载刚度：其中由G0推导得出；④正常固结的K0常数：=1 sinφ′；⑤失效折减系数：=1-RD/8 000，其中RD为砂土的相对密度。（3）对于砂土p-y曲线法的计算，其计算结果通过LPILE软件计算，需要参数包含土体重度、内摩擦角，均可通过室内土工试验数据得到。

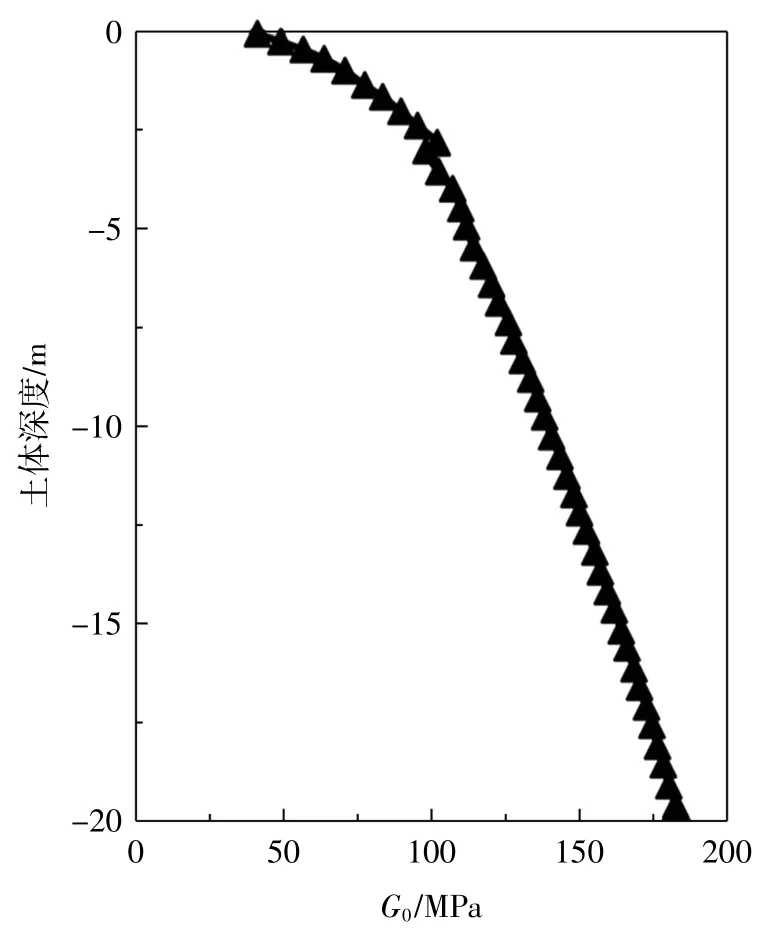
图2 G0值随土体深度变化曲线图[17]

表3 MC模型参数

表4 HS模型参数

2.3 不同计算方法的对比

本节将数值模拟计算结果进行整理，得到了MC模型、HS模型下大直径单桩基础荷载位移曲线和桩身变形曲线，并与p-y曲线法计算结果和PISA项目[13]模型试验结果进行比较，来探究不同计算方法在海上风电基础设计的差异性和适用性。

2.3.1 荷载—位移曲线的对比

图3为p-y曲线法、MC模型和HS模型3种计算方法下DL2单桩基础的水平荷载—位移曲线与试验结果的对比。由图可知，p-y曲线法和MC模型对应的水平荷载—位移曲线初始刚度都明显大于试验结果，且它们对应的水平泥面位移小于实验结果，HS模型的水平荷载—位移曲线与试验结果吻合较好。

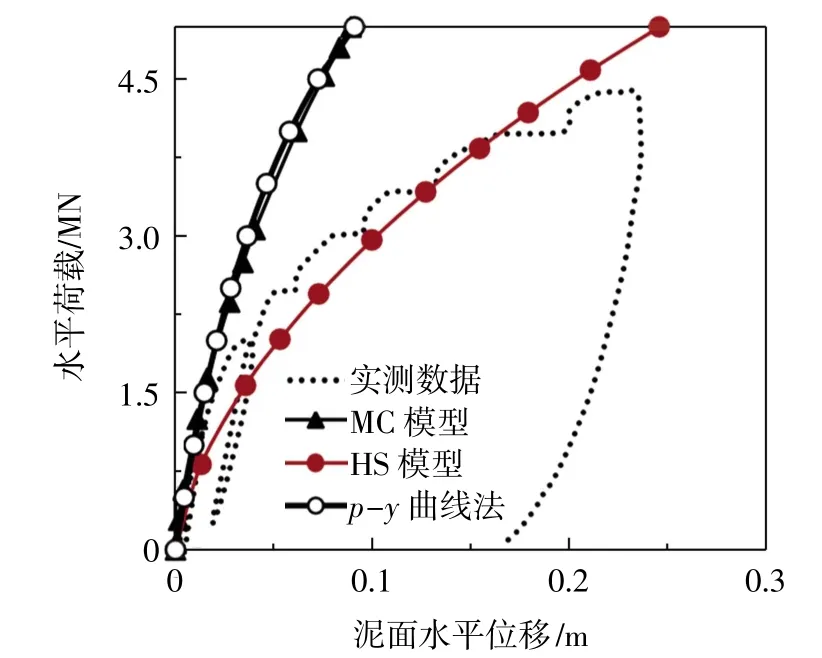
图3 DL2桩荷载—位移曲线

为了确定单桩基础极限水平承载力，研究者们提出了很多以桩基位移或桩基转角为标准的确定方法，其中ZDRAVKOVIˊC L等[18]研究发现当桩基泥面位移为0.1D时，桩基荷载位移曲线达到转点并逐渐平缓，如图4所示，进而认为桩基极限承载力应依据桩基泥面水平位移达到0.1D来确定，随后有研究表明该确定方法不会受到桩基长细比、偏心荷载等因素的影响[19]。因此本文分别选取图中泥面水平位移为0.1D时对应的水平荷载作为桩基水平极限承载力，因此本文分别选取图中泥面水平位移为0.1D时对应的水平荷载作为桩基水平极限承载力，以上三种计算方法的桩基水平极限承载力与试验结果具体对比情况如表5所示，p-y曲线法、MC模型、HS模型对应的DL2桩基水平极限承载力分别为6.25 MN、7.64 MN、4.46 MN，试验结果的DL2桩基水平极限承载力是4.2 MN，由表5可知，p-y曲线法和MC模型的水平极限承载力明显大于试验结果，HS模型对应的水平极限承载力与试验结果吻合程度较好，误差仅为6.2%。

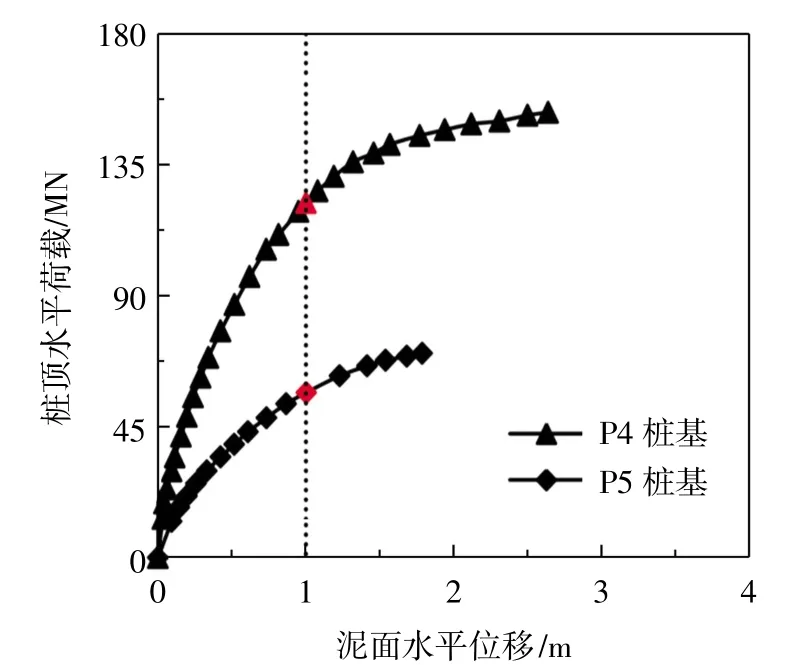
图4 桩荷载—位移曲线[19]

表5 不同计算方法下单桩水平极限承载力

这是由于p-y曲线法和MC模型都高估了土体实际初始地基刚度，并且MC模型没有考虑土体模量会随着应变衰减的特性，HS模型的塑性屈服面能够随着土体应力状态而改变，考虑了土体的压缩硬化和剪切硬化特性。

综上所述，在计算桩基础水平极限承载力时，p-y曲线法、MC模型计算结果过于保守，会导致桩基设计成本增高；而HS模型计算结果较为准确，可以较好地反映大直径桩基在水平极限承载力的水平位移。

2.3.2 桩身位移-埋深曲线的对比

图5 是不同水平荷载下的桩身位移—埋深曲线。由图可知，p-y曲线法、MC模型、HS模型计算结果和试验结果对应的桩身水平变形模式均为刚性转动，刚性转动点为泥面以下8 m处，这是由于该数值模型L/D=5.28，属于刚性桩[20]。图5（a）是水平荷载2.993 MN时p-y曲线法、MC模型、HS模型的桩身位移—埋深曲线与DL2单桩基础试验结果的对比。由图可知，p-y曲线法、MC模型、HS模型对应的桩体泥面位移分别是0.036 m、0.038 m、0.1 m，试验结果对应的桩体泥面位移是0.069 m。p-y曲线法和MC模型对应泥面水平位移分别小于试验结果的47.8%、45.2%，HS模型对应泥面水平位移大于试验结果的44.8%，可以看出HS模型计算结果与试验数据最为接近。图5（b）是水平荷载为3.97 MN时p-y曲线法、MC模型、HS模型的桩身位移—埋深曲线与试验结果的对比。由图5（b）可知，当水平荷载为3.97 MN时，p-y曲线法、MC模型、HS模型对应的桩体泥面位移分别是0.057 m、0.060 m、0.163 m，试验结果对应的桩体泥面位移是0.164 m。p-y曲线法、MC模型、HS模型对应的桩体泥面位移分别小于试验结果的65.2%、63.4%、0.6%；可以看出此时HS模型计算结果试验结果的误差仅为0.6%，可以较好地反映桩基在水平荷载作用下的桩基水平位移。通过图5（a）与图5（b）对比分析可知，由于p-y曲线法和MC模型都具有偏大的初始刚度，以及MC模型无法考虑土体硬化特性，HS模型虽低估了土体初始地基刚度，但能够考虑土体模量的非线性变化，从而HS模型计算结果与试验结果最为吻合。综上所述，HS模型计算结果曲线与试验结果最为吻合，表明了HS模型在海上风电基础极限承载力设计上的显著优势。

图5 DL2桩桩身位移曲线

3 桩土参数取值的影响

本节基于上述HS本构模型的单桩基础模型，建立了埋深24 m的直径为6 m的海上风电大直径单桩基础数值模型，水平极限承载力选取泥面位移为0.1D对应的水平荷载[18]，水平荷载施加在桩体伸出泥面9.9 m处，场地为均质砂土，砂土具体参数如表6所示。随后开展了桩土相关参数对海上风电大直径单桩基础极限承载力的影响规律研究。

表6 砂土参数

3.1 桩—土界面强度折减系数

PLAXIS中桩—土界面数值模拟是通过调节界面强度折减系数Rinter来实现，其中钢材与砂土的界面强度折减系数Rinter的取值范围为0.6～0.7[14]。为说明桩土相互作用对海上风电大直径基础水平承载力的影响，下文开展了强度折减系数Rinter对大直径单桩基础水平极限承载力的影响规律研究。

由图6可知，在砂土地基中，随着界面强度折减系数增加，桩基础水平极限承载力增大。这是由于界面强度是根据相邻的土体的强度参数进行折减来确定，桩—土界面强度折减系数增大，桩—土相互作用加强，从而桩基础水平极限承载力增大。

3.2 埋深

下面开展桩基埋深对基础水平极限承载力的影响规律研究，如图7所示。由图可知，随着钢管桩埋深增加，基础水平极限承载力也逐渐增大，当桩基埋深增加到48 m时，桩基水平极限承载力不再随着埋深增加而增大，并稳定于93.6 MN。主要原因是基础埋深增加，桩土相互作用面增大，桩基水平极限承载力增大，当桩基埋深增加到一定程度，桩土相互作用冗余度较高，因此桩基水平极限承载不再随着埋深增大而增加。

3.3 钢管桩桩径

图8 是钢管桩桩径对海上风电基础水平极限承载力的影响曲线。如图所示，随着桩径的增加，桩基水平极限承载力也在增大。当桩径从4 m增加到12 m，桩基水平极限承载力增大了518%。这是因为桩径增大，桩体抗弯刚度增大，且桩—土相互作用面增大导致桩—土相互作用增强，从而桩基水平极限承载力增大。

图8 桩径对桩基础水平极限承载力的影响

3.4 HS模型参数的影响

3.4.1 参照割线刚度

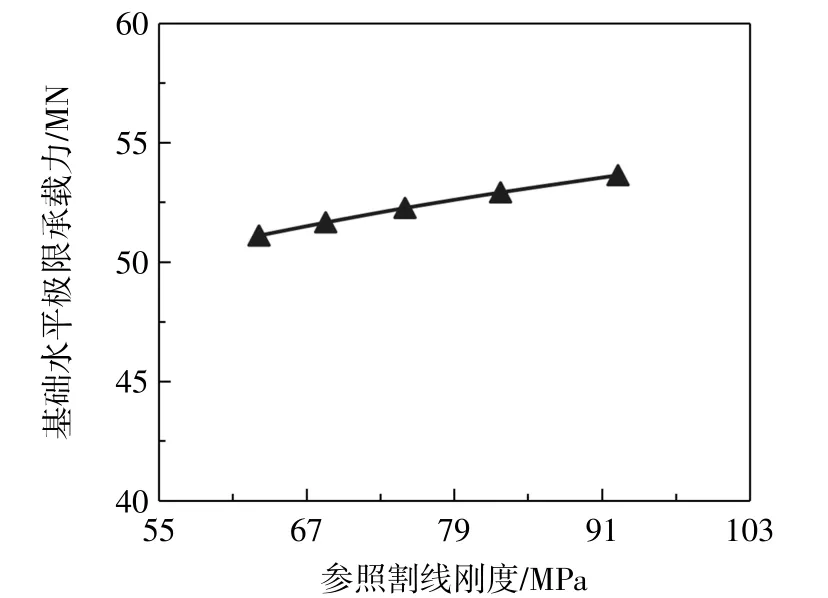
图9 参照割线刚度对桩基础水平极限承载力的影响

3.4.2 参照切线压缩刚度

图10 参照切线压缩刚度对桩基础水平极限承载力的影响

3.4.3 内摩擦角

图11是内摩擦角φ对基础水平极限承载力影响曲线。由图可知，随着内摩擦角的增大，基础水平极限承载逐渐增大。这是因为内摩擦角的增大，桩土相互作用面摩阻力增大，土体对桩体的约束力加强；砂土强度增大，地基承载力增大，因此基础水平极限承载力随着内摩擦角的增大而增大。

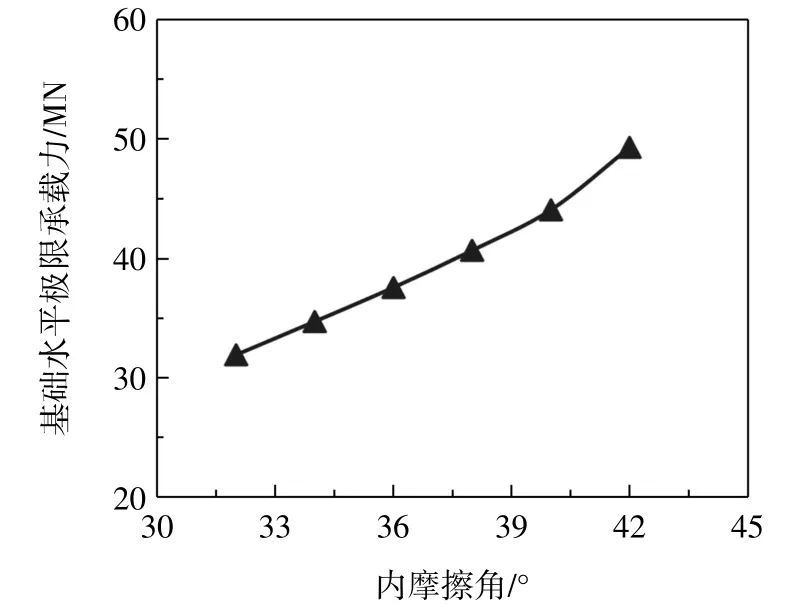
图11 内摩擦角对桩基础水平极限承载力的影响

3.4.4 剪胀角

图12是砂土剪胀角ψ对基础水平极限承载力影响曲线。由图可知，随着砂土剪胀角增大，基础水平极限承载力逐渐增大。这是因为砂土剪胀角的增大提高了土体的抗剪强度，提高了土体地基抗变形能力，从而桩基极限承载力增大。

图12 剪胀角对桩基础水平极限承载力的影响

3.5 桩土参数敏感性

为了对比桩土相关参数对基础水平极限承载力的影响敏感性程度，本文设定一个衡量指标——水平极限承载力变化率。水平极限承载力变化率的计算见式（2）。

式中，ΔFi为参数百分比变化对应的基础水平极限承载力百分比变化范围；Δxi为参数百分比变化范围。

由公式可知，水平极限承载力变化率的数值越大，代表其对应桩土相关参数对基础水平极限承载力的影响程度越大。基于以上理论，将各个参数调整±10%，计算对应的模型水平极限承载力，来探讨界面强度折减系数Rinter、桩基埋深L、桩径D、参照割线刚度、参照切线压缩刚度、内摩擦角φ、剪胀角ψ对海上风电大直径单桩基础水平承载能力的影响程度，如表7所示。

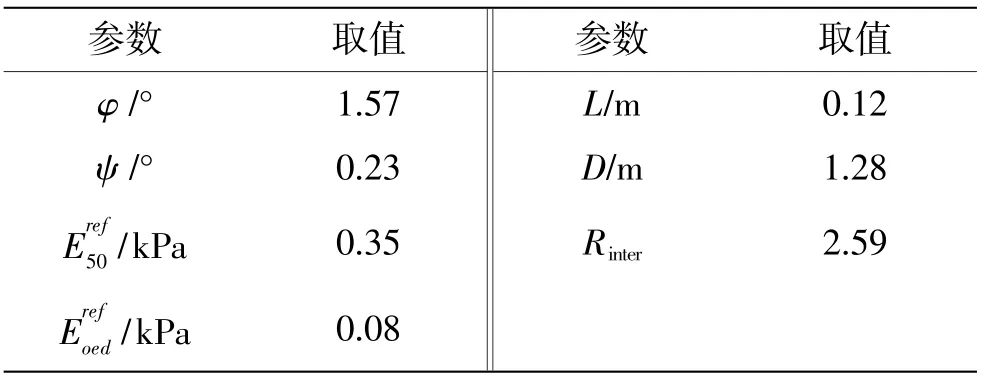
表7 不同桩土参数下基础水平极限承载力变化率

表7是砂土地基中埋深24 m的大直径单桩基础水平极限承载力变化率结果。由表7可知，在砂土地基中，钢管桩桩径对桩基水平极限承载力的影响最为显著，内摩擦角、埋深、参照切线压缩刚度、砂土剪胀角、界面强度折减系数、参照割线刚度对桩基水平极限承载力的影响依次减弱。

4 结 论

本文基于PISA项目[13]模型试验，利用PLAXIS3D有限元平台建立一系列的数值模型计算，并与p-y曲线法计算结果、试验结果比较，来探讨了p-y曲线法、MC模型、HS模型在海上风电大直径单桩水平承载计算的差异性和适用性，此外进一步研究了桩土重要因素对海上风电大直径桩基的水平承载特性影响规律，主要研究结论如下。

（1）HS模型对应的水平极限承载力与大直径单桩基础试验结果吻合程度较好，表明了HS模型在海上风电大直径单桩基础极限承载力设计上具有显著的优势。

（2）在砂土地基中，桩基础的埋深对基础水平极限承载力影响存在一个临界深度，小于临界深度，桩基水平极限承载力随着埋深增大而增大，大于临界深度时，桩基水平极限承载力增加幅度减小，趋于稳定。

（3）在砂土地基中，海上风电大直径单桩基础水平极限承载力随着界面强度折减系数、钢管桩桩径、内摩擦角、剪胀角、参照割线刚度、参照切线压缩刚度的增大而增大；此外钢管桩桩径对桩基极限水平承载力影响最为显著。