深井回采巷道底鼓变形与支承压力关系分析

谷拴成，王兴明，薛 蛟，牛宏新

(西安科技大学 建筑与土木工程学院，陕西 西安 710054)

随着我国煤矿开采逐年向深部发展，在浅部开采时岩体表现为硬岩的力学特性，而在深部开采时岩体表现出软岩的力学特征，致使巷道出现大变形、大地压、难支护等问题。底鼓是伴随矿井开采的一种常见现象，随着开采深度的增加巷道底鼓问题日趋严重，煤矿安全生产受到极大的威胁[1-2]。出现底鼓现象后，巷道内的行人、通风、运输、排水都将受到严重影响[3]。

杨仁树等[4]为研究软岩巷道底板层状特性对底鼓的影响，采用数值模拟与力学分析相结合的方法，对层状底板失稳机理进行了研究；高树生等[5]研究表明，造成底鼓严重的主要原因是回采期间巷道受工作面动压、两帮支护强度低及底板岩性差等影响；张官禹等[6]通过围岩变形监测与现场观察，认为底鼓的关键影响因素主要有底板岩性和结构状态、岩层应力、支护强度、水理作用等；孙晓明等[7]基于欧拉公式，利用压杆稳定理论、莫尔-库仑准则和挠曲破坏力学模型，研究了不同层状岩体巷道底鼓变形的破坏机理；文志杰等[8]根据巷道围岩本构关系及应力作用模式，建立了剪切错动型巷道底鼓力学模型，提出了巷道底鼓力源的计算方程；刘成等[9]分析了煤柱巷道围岩周边应力环境特征及其作用下的变形破坏形态；郑朋强等[10]认为巷道底鼓变形主要是软弱围岩在较高的水平构造应力作用下，产生明显的流变变形所致。

上述相关研究人员针对巷道底鼓机理提出了不同的分析方法，但是关于回采巷道底鼓变形与支承压力关系的分析还存在着许多不足[11-14]。因此，在总结其他学者研究成果的基础上，笔者以铜川玉华煤矿2407工作面回风巷道为研究对象，通过建立巷道底板等效载荷力学分析模型，推导出在支承压力作用下回风巷道底板最大底鼓量的表达式。研究成果可为相似地质环境下巷道底鼓的分析提供参考。

1 工程概况

铜川玉华煤矿2407工作面位于二盘区东翼，为二盘区第6个工作面。回采煤层为4-2煤层，赋存稳定，可采储量约为280.7万t。煤层埋深为600 m，厚度为4.63～7.34 m，平均厚度为6.87 m，煤层由运输巷道至回风巷道逐渐变薄，由终采线至开切眼逐渐变薄。煤层倾角为3°～9°，回采工作面走向长度为1 600 m，倾向长度为240 m。该工作面西南方向布置有盘区生产系统，东南方向毗邻2405工作面，西北方向为二盘区无煤带，东北方向为柴沟煤矿边界。

铜川玉华煤矿2407工作面巷道沿煤层走向布置，倾向布置有2条回采巷道，分别为运输巷道、回风巷道，2条巷道均与二盘区延伸巷道成垂直关系。2407回风巷道位于2405运输巷道以里，与2405运输巷道之间留设煤柱宽度为30 m，通过2407工作面回风巷道联络巷与第二回风巷道联通，主要用于掘进、回采期间2407工作面回风。2407工作面回风巷道空间位置如图1所示。

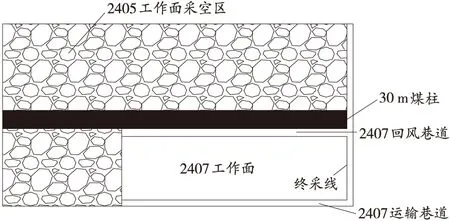
图1 2407工作面巷道空间位置图

2407工作面回风巷道顶板均采用锚网梁索支护，帮部采用锚网支护。锚杆间排距为800 mm×800 mm，帮部使用ø22 mm×2 250 mm麻花头圆钢锚杆，锚固长度350 mm，设计锚固力50 kN；顶板使用ø22 mm×2 600 mm左旋无纵筋螺纹钢锚杆，150 mm×150 mm×8 mm 拱形预应力钢托板，锚固长度700 mm，设计锚固力100 kN。锚索规格：索绳使用ø17.8 mm×8 000 mm预应力钢绞线，锚固长度1.4 m，设计锚固力200 kN，间排距为1 800 mm×1 800 mm。

2 矿山压力显现分析

2.1 支承压力分布

工作面回采过程中回采巷道围岩应力将重新分布，相邻煤柱和实体煤两侧的切向应力也随之改变，在工作面前方和回采巷道侧方形成支承压力[15]。工作面超前支承压力分布如图2所示，巷道两侧支承压力分布如图3所示。其中a为压力增高区、b为压力降低区、c为原岩应力区。

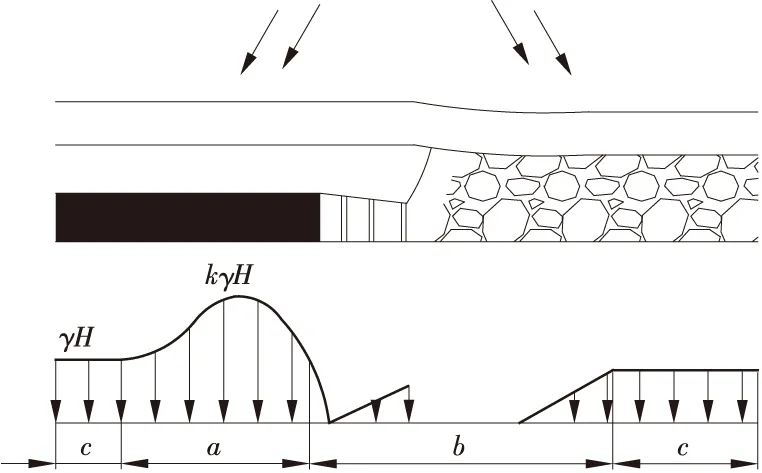
图2 工作面超前支承压力分布图

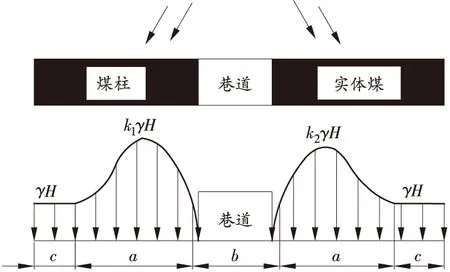
图3 巷道两侧支承压力分布图

2.2 巷道破坏特征

在2407工作面回采过程中，回风巷道发生了严重的破坏变形。根据现场观测结果，巷道破坏特征主要表现为：巷道底板变形量大于顶板变形量，最大底鼓量为1 250 mm，顶板最大位移量为85 mm，均位于巷道中部靠近煤柱一侧；巷道煤柱侧帮部和实体煤侧帮部变形量存在较大差异，煤柱帮最大变形量为315 mm，实体煤帮最大变形量为207 mm。巷道底鼓现象比较严重，导致巷道内的行人、通风、运输受到严重影响，现场需要采用挖底、扩帮等措施才能满足正常生产需要。

笔者主要分析2407工作面回采过程中巷道两侧形成的支承压力对巷道底板变形的影响，不考虑工作面前方形成的超前支承压力对巷道底板变形的影响。

3 支承压力引起巷道底鼓

3.1 巷道底板力学模型建立

工作面回采过程中巷道围岩应力将重新分布，巷道底板在煤帮两侧支承压力作用下将出现底鼓现象。工作面回采后巷道的最终应力状态由初始应力状态和回采过程产生的应力状态构成。由于初始应力状态下巷道不产生变形，则工作面回采后巷道的最终变形量由回采过程中产生的变形量决定[16]。假设煤柱和实体煤两侧的支承压力分布相同，为了计算方便，对煤壁两侧压力增高区载荷及压力降低区载荷进行线性简化。以巷道底板中心为原点，沿巷道水平向右为x轴正方向，垂直底板向下为y轴正方向，建立直角坐标系。在建立模型过程中，将引入等效载荷的概念，巷道底板等效载荷的力学模型如图4所示。

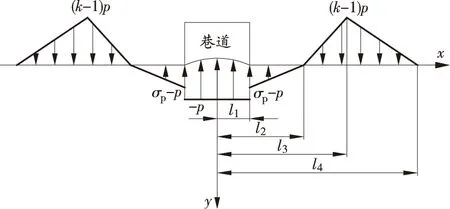
图4 巷道底板等效载荷力学模型

3.2 确定支承压力作用下巷道底鼓量

根据图4建立的巷道底板力学模型，可得在支承压力作用下底板所承受的载荷为：

(1)

式中：l1为巷道宽度的一半，m；l2为煤帮破裂区到巷道中心的距离，m；l3为煤帮塑性区到巷道中心的距离，m；l4为煤帮弹性区到巷道中心的距离，m；k为集中应力系数；p为原岩应力，MPa；σp为巷道煤壁对底板的作用力，MPa。

由弹性力学可知，为了保证位移分量u和w的存在，变形分量必须满足相容方程[17]，即：

(2)

(3)

式中：εx、εy分别为x和y方向的线应变；γxy为x与y两正方向的切应变；σx、σy分别为x和y方向的应力；fx、fy分别为x和y方向的岩体体力分量；μ为泊松比。

由于底板岩体体力分量fx、fy为常量，则式(3)可简化为：

(4)

由弹性力学可知，在体力不变的情况下，存在一个应力函数Φ，满足重调和方程：

(5)

应力函数与应力分量σx、σy、τxy的关系为：

(6)

根据几何方程和物理方程可以确定位移分量：

(7)

式中：G为切变模量，MPa；τxy为x与y两正方向的切应力,MPa。

巷道底板表面处，边界条件为：

(8)

式中：p(x)为巷道底板所承受的载荷，MPa；w为巷道底板垂直方向位移量，m。

求解过程中，采用傅里叶积分变换方法中的余弦和正弦变换，函数f(t)的傅里叶积分变换公式如下[18]：

(9)

其对应的逆变换公式为：

(10)

根据式(9)对式(5)～(7)进行傅里叶余弦或正弦变换，则位移分量的傅里叶变换式如下：

(11)

式中A、B为积分常数。

根据巷道底板表面处的边界条件可确定出积分常数A、B，则可以得到巷道底板位移表达式：

(12)

式中J1(·)为第一类1阶贝塞尔函数。

由式(12)中的第2式可得，巷道底板岩层表面处的位移为：

(13)

利用贝塞尔函数的性质，可以得出在支承压力作用下，巷道底板最大底鼓量为：

(14)

式中：E为弹性模量，GPa；γ为岩层平均重度，kN/m3；H为煤层埋深，m。

分析式(14)可知，在支承压力作用下，巷道底板最大底鼓量发生在巷道中心位置，并且巷道底板最大底鼓量与底板弹性模量呈负相关关系；与底板泊松比的平方呈负相关关系；与上覆岩层载荷γH呈正相关关系；与煤帮弹性区到巷道中心的距离呈正相关关系。

根据玉华煤矿2407工作面回风巷道矿压显现规律、围岩特性、地质环境等条件,取泊松比μ=0.4,弹性模量E=1 GPa,H=600 m,γ=23 kN/m3,煤帮弹性区到巷道中心的距离l4=36 m。

将上述参数值代入到式(14)中可以计算出由支承压力产生的底鼓量为192 mm。现场监测得到巷道总底鼓量为1 250 mm，则支承压力引起的巷道底鼓量占总底鼓量的15.4%。

4 数值模拟分析

4.1 建立数值模型

采用FLAC3D数值模拟软件对玉华煤矿2407工作面回风巷道进行数值计算分析。模型设计为 120 m(x轴)×80 m (y轴)×45 m (z轴)，共划分 64 000 个单元、68 630个节点。模拟过程中，采用Mohr-Coulomb模型，选择大应变模式。模型上表面采用应力边界条件，上表面按上覆岩层的自重计算，施加相对应的垂直应力13.8 MPa，水平应力16.5 MPa。底面固定，4个侧面限制水平位移，计算过程首先建立模型，然后生成原岩应力场，开挖巷道并支护，最后进行回采工作面计算。数值计算模型如图5所示。

图5 回风巷道数值计算模型图

2407工作面直接顶为粉砂岩、细砂岩，水平及波状层理，见植物根茎化石，厚度为3.50～10.72 m，平均厚度为6.45 m，属于中等坚硬至极不坚硬顶板；老顶为细砂岩、中砂岩，局部老顶中含砾石，平均厚度为12.90 m，属于中等稳定顶板；伪顶为泥岩、砂质泥岩，厚度为0.30～0.70 m，平均厚度为0.50 m；煤层为4-2煤，以半亮型为主，沥青光泽；直接底板为泥岩、炭质泥岩，厚度为0.80～2.51 m，一般厚度为1.40 m；其下为根土岩、砂质泥岩，厚度为2.50～14.62 m，一般厚度为9.52 m。

煤层及顶底板岩层力学参数如表1所示。

表1 煤岩层力学参数

4.2 煤柱宽度对底鼓的影响

工作面回采过程中，巷道围岩应力将重新分布，相邻煤柱和实体煤两侧的切向应力也随之改变。通过现场观测了解到2407工作面回风巷道底板破坏比较严重，并且煤柱帮底部也发生了破坏。分析可知，回风巷道底鼓现象严重的原因可能是由于邻近采空区煤柱宽度留设过大导致工作面回采过程中应力叠加所致。因此，分析不同煤柱宽度下巷道两帮煤柱侧及煤壁侧垂直应力分布有重要意义。采用FLAC3D软件模拟计算得到不同煤柱宽度下2407工作面回风巷道两帮煤柱侧及煤壁侧垂直应力分布曲线，如图6所示。

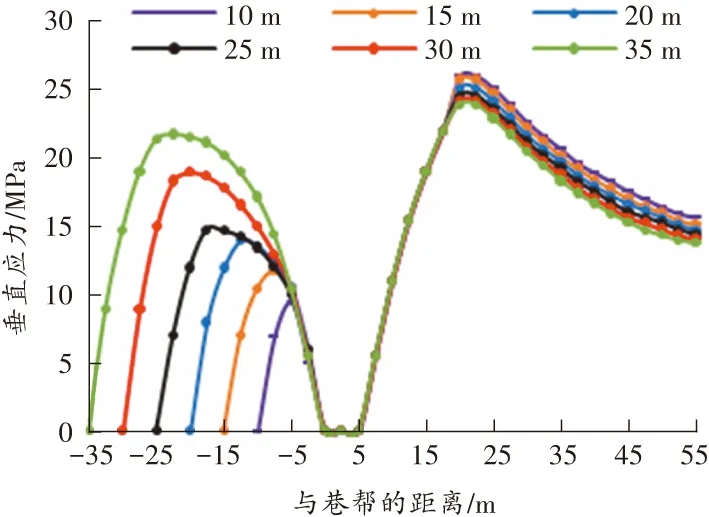
图6 不同宽度煤柱下回风巷道两帮煤柱侧及煤壁侧垂直应力分布曲线

由图6可知，当煤柱宽度不同时，煤柱侧和煤壁侧所受的垂直应力也不同。随着煤柱宽度增大，煤壁侧所受应力逐渐降低，煤柱侧所受应力逐渐增高。当煤柱宽度为10、15、20 m时，煤柱所受应力全部低于原岩应力；当煤柱宽度为 25 m 时，煤柱内垂直应力峰值为14.8 MPa，煤柱具有明显承载能力，并且煤柱内垂直应力呈对称分布；当煤柱宽度为30、35 m时，煤柱大部分范围所受应力高于原岩应力，并且呈现不同幅度增大。巷道煤壁侧垂直应力增高部分影响范围达55 m。

通过上述分析可知，工作面回采过程中煤柱所受应力随着煤柱宽度的增加而呈不同幅度增大。为避免因采动导致煤柱内垂直应力增大而对巷道产生的影响，煤柱宽度不宜大于25 m。当煤柱宽度为 25 m 时，在工作面回采过程中，支承压力对巷道底板破坏的影响最小。

5 现场观测

5.1 塑性区范围分析

为了得到煤柱侧和煤壁侧帮部塑性区范围，现场采用钻孔窥视仪对巷道两帮进行观测。2407工作面回风巷道煤柱侧帮部不同位置破坏区探测图如图7 所示。

(a)6.0 m(b)4.0 m

(c)3.0 m(d)0.5 m

由图7可知，在煤柱侧帮部6.0 m处，巷道还未发生破坏，围岩比较完整；在煤柱侧帮部3.0～0.5 m内，巷道围岩出现不连续情况，说明塑性区范围在3.0～0.5 m；在煤柱侧帮部0～0.5 m内，巷道围岩基本已经全部破碎，则此区域为围岩破碎区。

2407工作面回风巷道煤壁侧帮部不同位置破坏区探测图如图8所示。

(a)6.0 m(b)4.0 m

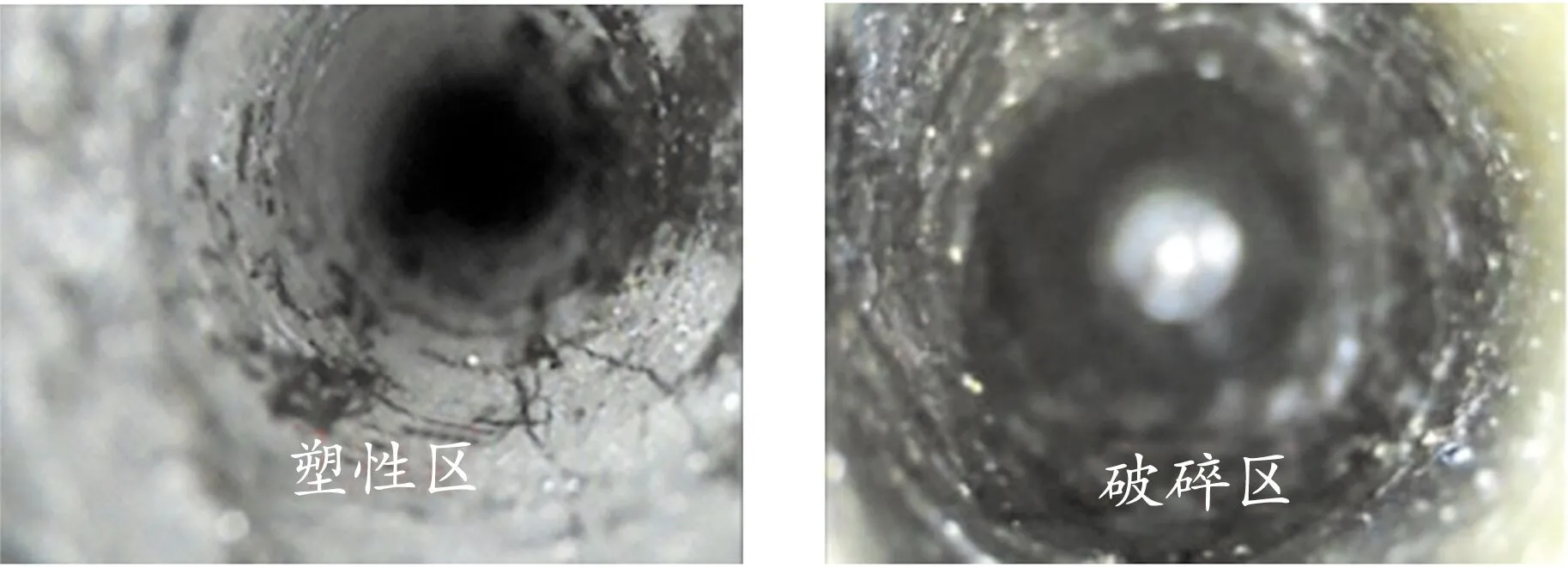
(c)2.5 m(d)0.5 m

由图8可知，在煤壁侧帮部6.0～2.5 m内，巷道还未发生破坏，围岩比较完整；在煤壁侧帮部 2.5 m处，巷道围岩逐渐出现破坏区；在煤壁侧帮部2.5～0.5 m内，巷道围岩出现不连续情况，说明塑性区范围在2.5～0.5 m；在煤壁侧帮部0～0.5 m内，巷道围岩基本全部破碎，则此区域为围岩破碎区。

综上分析可知，受深井回采巷道工作面采动影响，靠近采空区一侧的围岩比远离采空区一侧的围岩变形要大，并且塑性区范围也较大。这是由于采动应力在传递时巷道起到了卸压槽的作用，使得应力传递被中断。

5.2 工业性试验分析

根据研究成果，进行现场工业性试验分析。铜川玉华煤矿2403工作面位于二盘区东翼，工作面回风巷道煤柱留设宽度为25 m，其地质情况与2407工作面类似。在巷道中距离回采工作面80 m处布置矿压观测站，在测站内顶板、底板、煤柱帮、煤壁帮均匀布置矿压观测点，监测2403工作面回采期间巷道围岩变形量，结果如图9所示。

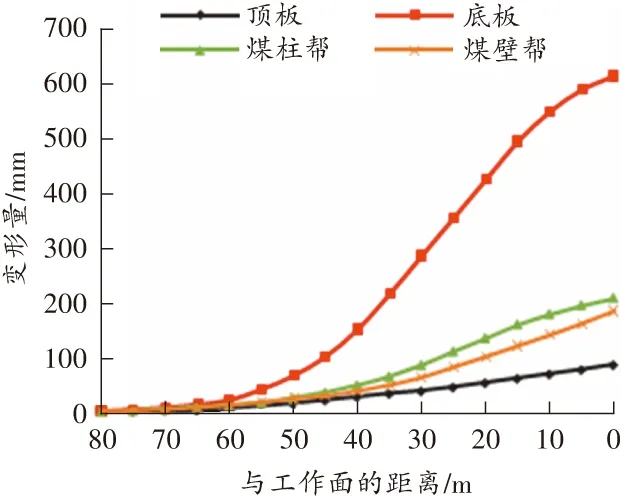
图9 巷道围岩变形量监测曲线

由图9可知，顶板最大下沉量为86 mm，底板最大底鼓量为615 mm，煤柱侧帮部最大变形量为 207 m，煤壁侧帮部最大变形量为184 m。2403工作面回采巷道内行人、通风、运输、排水都能够正常进行，巷道围岩变形控制效果较好。实践表明，煤柱尺寸对巷道围岩变形具有一定的影响，留设25 m煤柱与留设30 m煤柱相比较，巷道底鼓量明显减小。

6 结论

1)工作面回采过程中在巷道两侧形成固定支承压力，通过建立巷道底板力学分析模型，推导出在支承压力作用下巷道底板最大底鼓量的表达式。经计算，支承压力引起的巷道底鼓量占总底鼓量的15.4%。

2)通过FLAC3D软件模拟得到不同宽度煤柱条件下巷道煤柱侧及煤壁侧垂直应力分布。当煤柱宽度为25 m时可减小采动影响，支承压力对巷道底鼓变形的影响最小。

3)在采动影响下，巷道两侧帮部塑性区呈不对称分布。煤柱侧帮部塑性区范围较大，煤壁侧帮部塑性区范围较小。说明采动应力在传递时巷道起到了卸压槽的作用，使得应力传递被中断。