耦合效应下的煤矿顶板事故风险因素评价研究

王慧雯，薛 晔，薛崇义

(太原理工大学 经济管理学院，山西 太原 030024)

我国煤矿顶板事故是发生次数和死亡人数最多的煤矿生产事故[1]。如何对煤矿顶板事故进行科学有效的预防一直是一个重要课题。其难度在于：一是没有科学的方法去量化风险因素，风险信息具有模糊性，尤其是在人为因素和管理因素的量化过程中，往往具有很强的主观偏好；二是人为(人)、设备(机)、环境(环)、管理(管)四大因素对煤矿顶板事故风险的作用不是线性相加，而是存在多种类型的耦合作用。因此，如何有效识别重要的风险因素及其耦合类型对煤矿顶板事故的防范具有重要意义。

目前，关于煤矿顶板事故风险分析的研究主要有：王琦等[2]从地质角度分析了煤矿顶板事故的原因和机理，提出了基于超前地质预报的煤矿顶板事故支护预案防治方法；姬亚东[3]运用聚类分析对煤矿顶板涌水的关键因素进行分区，并进一步采用模糊综合评价法将煤矿顶板涌水风险划分为4个等级；李博杨等[4]建立了煤矿顶板事故风险的评价指标，并集合灰色关联法和集对分析法对顶板事故风险进行了评价；高平等[5]利用行为安全“2-4”模型分析了煤矿顶板事故的不安全动作，结果表明“违章指挥”和“未检查工作环境”是顶板事故的主要不安全动作；李海丽等[6]基于系统动力学等方法提出了一种矿山顶板事故风险的分析方法，可以寻找风险防范中的不足；明崯崯等[7]总结出煤矿顶板事故的24种影响因素，并利用ISM法研究了煤矿顶板系统的多级递阶系统；李贤功等[8]结合相关性分析和k2算法，建立了顶板事故原因分析的贝叶斯网络模型，并分析了各因素对顶板事故的影响程度；陈晓勇等[9]基于G1-DEMATEL法定量分析了煤矿顶板事故的风险因素，结果表明“内部管理机制”和“违章指挥”是煤矿顶板事故风险的关键因素。

综上所述，当前关于煤矿顶板事故的风险分析已取得丰富成果，但是较少能综合考虑风险信息模糊性和因素间的交互耦合效应，因此笔者利用复杂系统的通用分析工具N-K模型量化煤矿顶板事故风险因素耦合效应，针对风险信息的模糊性，构建基于直觉模糊集和逼近理想求解模型(TOPSIS)的煤矿顶板风险因素的评价模型，并对我国2008—2018年发生的185起典型煤矿顶板事故进行实例分析，以得到影响煤矿顶板事故的关键风险因素和主要耦合形式，为煤矿顶板事故的科学防范提供参考。

1 煤矿顶板事故风险因素的耦合效应

1.1 风险因素的耦合分析

当系统中拥有两个或两个以上元素时，如果风险因素相互影响会增加风险强度，即使系统中各个因素的风险线性相加未能突破阈值，也会导致风险事故发生，这就是风险演化过程中重要的风险因素耦合效应[10]。煤矿生产系统是一个复杂的社会技术系统，在生产过程中有许多煤矿顶板事故风险因素，根据相关研究成果及事故致因理论[11]，风险因素可分为人为因素、设备因素、环境因素和管理因素四大类。依据相关的研究成果，可将煤矿顶板事故的风险因素的耦合分为单因素耦合、双因素耦合、多因素耦合3种类型[12]，具体见图1。由于煤矿顶板事故风险中单因素耦合风险明显较低，而4个因素之间的耦合又涉及到全部风险因素，因此笔者在对各风险因素的评价研究中只讨论双因素耦合和三因素耦合情况。

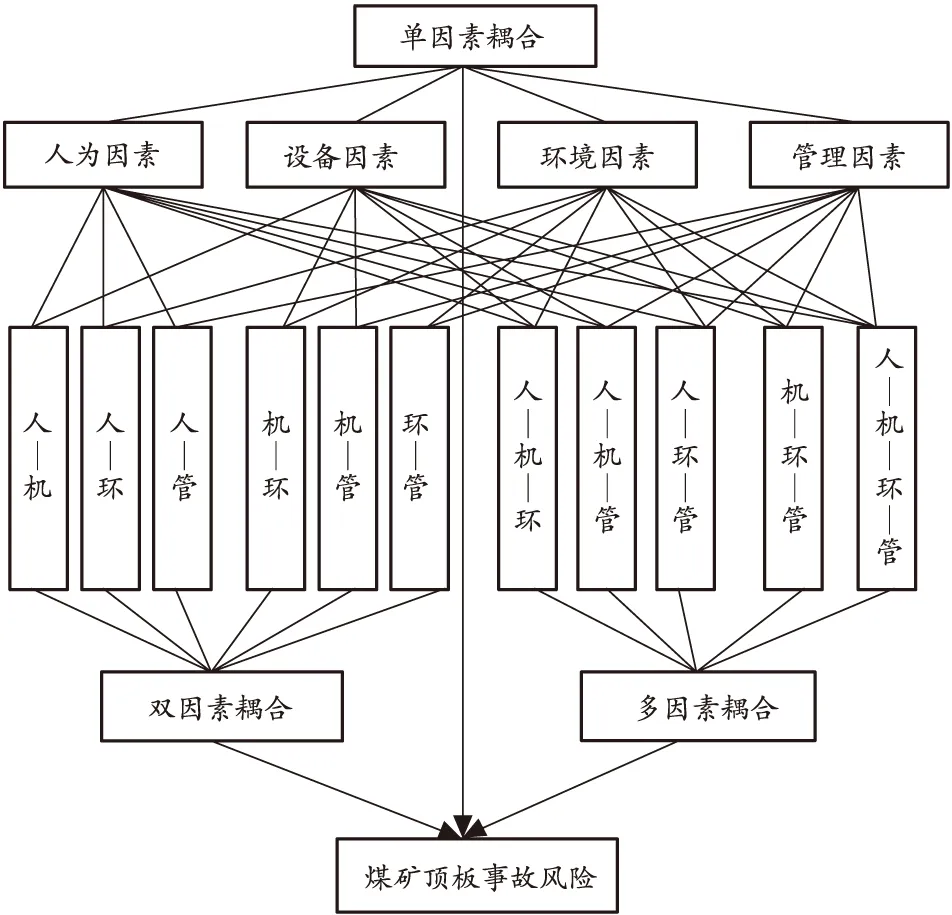
图1 煤矿顶板事故的风险因素耦合类型

1.2 风险因素耦合N-K网络量化模型

N-K网络量化模型常用于复杂动态系统，在煤矿的水灾和瓦斯事故风险分析方面已经得到应用[13-15]。煤矿顶板事故的引发也是复杂系统中风险因素耦合变化的结果，因此可以用N-K模型来量化煤矿顶板事故中的风险因素耦合效应。在N-K模型中N是系统中元素的个数，K是系统中相互耦合关系的个数，若每个元素有n种状态，则系统共有nN种耦合形式。N-K模型通过计算N类因素的交互信息T来量化因素耦合后对系统的影响程度。在已发生的系统故障记录中，若某种类型耦合形式的频数高，则该类型耦合形式引起系统风险的可能性更大。N-K模型根据信息理论的知识计算N类因素的交互信息T，具体公式如下[16]：

(1)

式中：x1,x2,…,xN是系统中包含的N个因素；I表示各因素的状态，每个因素有n种状态;PI1PI2…PIN为当因素x1在状态I1，x2在状态I2,…,xN在状态IN时发生风险事故的概率。

T(x1,x2,…,xN)表示因素x1～xN的N个因素耦合效应评价值，其值越高，证明此N类因素耦合时发生风险事故的概率越高，对系统的整体影响越大。

同理，可计算该系统中任意N-1,N-2,…,2个因素耦合效应的评价值。

将N-K模型应用到煤矿顶板事故中，设事故的4类风险因素人、机、环和管为xj(j=1,2,3,4)，风险因素xj的状态共有两种，记为Ij，Ij=0表示风险因素xj不存在，Ij=1表示存在风险因素xj，系统共有6种双因素耦合效应类型和4种三因素耦合效应类型，根据N-K模型，各类型耦合效应的评价值T的计算公式(以T(x1,x2)和T(x1,x2,x3)为例)如下：

(2)

2 煤矿顶板事故风险因素的评价

2.1 加权直觉模糊集决策矩阵建立

煤矿顶板事故的人、机、环、管四大影响因素参与的双因素耦合效应和三因素耦合效应可被视为因素的两种属性，设煤矿顶板事故的4类风险因素均有2个属性oi(i=1,2)，风险因素xj关于属性oi的值记为aij，a1j表示风险因素xj参与双因素耦合效应评价值之和，a2j表示风险因素xj参与三因素耦合效应评价值之和。aij的计算公式(以a11和a21为例)如下：

(3)

对四大风险因素的评价可转换为多属性决策问题，首先需要构建决策矩阵[17]，步骤如下：

1)计算aij转换后的直觉模糊集Fij〈uij,vij〉，uij和vij计算公式如下：

(4)

式中:uij和vij为风险因素xj关于属性oi的隶属度和非隶属度，uij∈[0,1]，vij∈[0,1]，且0≤uij+vij≤1；αi和βi为根据实际情况设定的参数，αi∈[0,1]，βi∈[0,1]，且0≤αi+βi≤1。

2)计算属性oi的权重ωi。根据离差最大化思想，采用直觉模糊集的距离公式计算各属性权重[18]，计算方法具体如下：

(5)

(6)

式中：d(Fij,Fik)为直觉模糊集Fij〈uij,vij〉与Fik〈uik,vik〉之间的距离；πij为直觉模糊集Fij〈uij,vij〉的犹豫度，πij=1-uij-vij。

(7)

2.2 基于TOPSIS的风险因素评价模型

TOPSIS(Technique for Order Preference by Similarity to Ideal Solution)是在多目标决策分析中常用的一种模型，其基本思路是根据现有决策方案得出正理想解和负理想解，然后通过计算分析所有决策方案与正理想解的相对逼近程度来得到各种方案的评价值，因此也称逼近理想求解法[19]。该模型对样本量无特别要求，无参考序列干扰，计算结果更加客观，将该模型与直觉模糊集相结合，使具有模糊性的风险信息得到更加准确的评价[20]。故笔者在前文构建的加权直觉模糊集决策矩阵基础上，基于TOPSIS模型提出了耦合效应下煤矿顶板事故风险因素的评价方法，具体过程如下：

1)计算直觉模糊集正负理想解向量A+和A-。其计算公式如下：

(8)

2)计算风险因素xj两个属性的评价值向量Aj与A+、A-的欧几里得距离d(Aj,A+)与d(Aj,A-):

(9)

3)计算风险因素xj的综合评价值φj:

(10)

φj越大，代表风险因素xj两个属性的评价值向量Aj与最优解向量A+的相对贴近度越高，证明风险因素xj对煤矿顶板事故的影响越大。

3 案例分析

3.1 耦合效应下的风险因素评价

根据国家相关部门公布的煤矿顶板事故调查报告，统计出我国2008—2018年185起典型煤矿顶板事故的发生原因，并根据人、机、环、管四大风险因素进行归类，进一步计算每一类风险因素耦合形式的发生的次数f和频率P，以频率P的值表示各类风险因素耦合形式引起顶板事故的概率，结果如表1所示。

表1 煤矿顶板事故中不同风险因素耦合类型的次数和频率

1)将表1的数据代入式(2)，可计算得到各风险因素耦合形式的评价值T(x1,x2,…,xn)：T(x1,x2)=0.046 130，T(x1,x3)=0.027 981，T(x1,x4)=0.009 388，T(x2,x3)=0.027 674，T(x2,x4)=0.043 211，T(x3,x4)=0.030 125，T(x1,x2,x3)=0.085 001，T(x1,x2,x4)=0.082 039，T(x1,x3,x4)=0.077 031，T(x2,x3,x4)=0.086 184。

2)将评价值T(x1,x2,…,xn)代入式(3)，可计算得到各风险因素的属性值aij，结果见表2。

表2 各风险因素的属性值

3)将属性值aij代入式(4)转换为直觉模糊集，经比较判断选取α1=α2=0.8，β1=β2=0.1，得到初步的直觉模糊集决策矩阵F：

F=(〈uij,vij〉)2×4

4)将决策矩阵F的信息代入式(5)和(6)，计算得到属性权重ω：ω1=0.465，ω2=0.535。

A+=(〈0.372,0.033〉,〈0.428,0.035〉)T；

A-=(〈0.263,0.047〉,〈0.282,0.053〉)T。

d(A1,A+)=0.180，d(A1,A-)=0.022；

d(A2,A+)=0.023，d(A2,A-)=0.182；

d(A3,A+)=0.100，d(A3,A-)=0.137；

d(A4,A+)=0.110，d(A4,A-)=0.132。

8)将d(Aj,A+)与d(Aj,A-)代入式(10)，计算得到风险因素xj的综合评价值φj：

φ1=0.891，φ2=0.111，φ3=0.421，φ4=0.455。

因此，影响煤矿顶板事故的四大风险因素的重要性排序为φ1>φ4>φ3>φ2。

3.2 计算结果分析

1)根据N-K网络量化模型计算的各风险因素耦合类型的耦合效应评价值T可知，耦合风险因素的增加会增大煤矿顶板事故的风险。在双因素耦合类型中，人为因素和设备因素耦合的风险最高，设备因素与管理因素耦合风险相对较高，表明当设备状况较差时，主观因素(人为操作或管理不当)容易引起顶板事故。在三因素耦合类型中，设备因素、环境因素和管理因素耦合的风险最高，设备因素、环境因素和人为因素耦合的风险相对较高，表明当两个客观因素(设备状态不良和环境较差)完全耦合时，任一主观因素均易引起顶板事故。

2)根据直觉模糊集和TOPSIS的风险因素综合评价值φj可知，人为因素>管理因素>环境因素>设备因素。结合耦合效应评价值T表明，客观因素是煤矿顶板事故风险的基础性因素，较少能单独引发煤矿顶板事故；主观因素是煤矿顶板事故风险的活跃因素，往往和客观因素耦合时会增大风险。

4 结论

1)根据N-K模型计算的不同风险因素耦合效应的评价值，可以有效地表征风险因素间交互耦合时的煤矿顶板事故风险态势。

2)直觉模糊集可以有效地处理煤矿顶板事故风险因素的不确定信息，将风险因素的评价转换为直觉模糊集多属性决策问题。

3)根据TOPSIS模型，建立了耦合效应下煤矿顶板事故风险因素的评价模型，利用该模型可以有效地评价各风险因素对煤矿顶板事故风险防范的重要性。

4)根据实例分析结果，主观因素，尤其是人为因素是顶板事故风险的决定性因素，因此要加强顶板安全教育培训,规范相关安全操作，提高人员自我保护意识。客观因素是顶板事故风险的基础性因素，要全方位保障设备的良好状态和环境的稳定性。