选煤厂原煤仓瓦斯超限治理研究

马 恒，郭 瑶，梁腾飞，艾纯明

(1.辽宁工程技术大学 安全科学与工程学院，辽宁 阜新 123000；2.矿山热动力灾害与防治教育部重点实验室，辽宁 阜新 123000)

在选煤厂原煤仓中，煤粒的存在方式和采空区的遗落煤有相似之处，都属于多孔介质的范畴[1]。前苏联学者[2]开创性地应用达西定律—线性渗透定律描述了瓦斯在煤层内的运动状态；我国学者周世宁等[3]首次将多孔介质理论应用于煤层中，开辟了运用渗流理论治理煤层瓦斯的先河。针对原煤仓瓦斯超限问题，李丹天等[4]提出将通风口设置在原煤仓顶部的方案，以减少煤仓内积累的瓦斯，为原煤仓瓦斯的治理提出了新的优化思路；郭亚迪等[5]对原煤仓进行正压通风和负压抽风联合改造，从理论上证明了混合式通风治理瓦斯的可行性；王兵建等[6]对圆筒煤仓仓下瓦斯积聚的原因和分布规律进行了研究，为选煤厂制订防范措施提供了理论依据。笔者以铁东选煤厂原煤仓为例，对原煤仓内部瓦斯涌出规律进行数值模拟，以期得出煤仓内部瓦斯的分布规律，通过对不同通风方式与风速的方案模拟结果进行分析对比，得出治理原煤仓瓦斯超限的优化方案，可为其他选煤厂原煤仓治理瓦斯超限提供参考。

1 选煤厂原煤仓数值模拟

1.1 数学模型的建立

原煤仓内部气体的流动方式是间断式流动，将其视为空气在多孔介质区域的运动，使用间断空间区域的计算方程[7]。使用模型为选煤厂原煤仓，由煤堆叠形成的空间可被视为多孔介质，其孔隙率取值范围为0～1。

1)组分运输方程

原煤仓内的气体是空气和瓦斯的混合气体，而由于在原煤仓中堆叠的煤体会不断地涌出瓦斯，改变了原煤仓内预混气体的组分浓度[8]。在该过程中，所有组分之间符合组分质量守恒定律[9]：

(1)

式中：t为时间，s；ρ为气体密度，kg/m3；Yi为质量分数；v为速度，m/s；Ri为反应产生净速率；Si为组分生产率；Ji为扩散通量，由Fick定律[10-11]给出。

在湍流模型中，扩散通量表达式为：

(2)

式中：Di,m为质量扩散系数；μt为动力黏度，Pa·s；Sct为湍流施密特数，取值0.7；DT,i为热扩散系数；T为温度，K。

2)原煤仓控制微分方程

将原煤仓内空间看作具有梯度变化的渗流空间，通过引入的空度因子在多孔介质中应用质量守恒定律和纳维斯托克斯方程[12-13]，假设气体密度不发生改变，不受紊流效应的干扰，可以导出：

(3)

式中：ui、uj为速度分量，m/s；xi、xj为渗流方向；gi为加速度分量，m/s2；p为气体压力，Pa；μ为黏性系数，kg/(m·s)；Fi为瓦斯流动阻力，Pa/m。

1.2 原煤仓物理模型建立及边界条件确定

物理模型选取铁东选煤厂1号原煤仓，根据实际测量数据，将原煤仓分为3个部分：第1部分为原煤仓放煤口的倒圆台形结构，圆台高8 m，上、下部直径分别为20、3 m；第2部分为圆柱体结构，高度为38 m，其直径与圆台上部直径相同；第3部分为圆柱体结构，其上部的3个正方形窗口，边长为3 m，其中2个对立的窗口为通风口，另一个窗口为原煤进口。仓内为半封闭状态，底部煤体赋存了大量瓦斯，易导致煤仓内瓦斯浓度(甲烷体积分数，下同)超标，遇明火易引发爆炸事故。

采用有限体积法中的拓扑划分方式对原煤仓进行网格划分，采用自适应性网格。网格总数为20万个，将原煤仓划分成12个区域，第1部分底部区域划分为 44 644个网格；第2部分圆柱体部分划分为10个区域，且每个区域网格数量一致，均为 11 065个；第3部分中通风口和进煤口附近区域划分为 9 751个网格。原煤仓网格划分如图1所示。

图1 原煤仓网格划分图

边界条件主要为进出风口，将进煤口设定为风量进口，采用速度入口的方式，即VELOCITY-INLET；2个出风口不采取机械通风的方式，而是将其定义为自由出口，且出口使用率为1。数值模拟条件设置情况见表1。

表1 数值模拟条件设定

多孔介质孔隙率计算公式如下：

q=1-1/kp

(4)

式中：q为多孔介质孔隙率；kp为碎胀系数，取经验值1.3。

通过计算得到原煤仓煤体之间的孔隙率q=0.231。原煤仓内煤堆叠的方式呈线性变化，因此孔隙率也呈线性变化，在物理建模和网格划分过程中单独定义12个计算区域的孔隙率，将h=15 m处计算区域的孔隙率设为0.231，计算区域每升高或降低一个区域孔隙率增加或减少0.020，其值增加或减少0.020，这样可保证模拟结果的准确性。

原煤仓内涉及多孔介质流动问题，将黏性损失与惯性损失之和作为动量守恒方程[14]中的附加动量损失源项。1/k为黏性损失系数，f为惯性损失系数，其计算公式如下：

(5)

(6)

式中：k为多孔介质渗透率，m2；b为原煤仓煤体平均粒径，m。

1.3 原煤仓源项确立

为研究瓦斯在原煤仓内的运移规律，在原煤仓进煤口进行实地采样，原煤仓内部瓦斯的平均涌出量[15]Q0如表2所示。

表2 原煤仓瓦斯涌出量

通过计算得到原煤仓内瓦斯密度ρ为0.7 kg/m3，原煤仓内煤体的总体积Vc为9 420 m3，在Fluent模拟计算中煤体解吸出的瓦斯量q源被视为源项，其计算公式如下：

(7)

式中：q源为原煤源项，kg/(m3·s)；Q0为瓦斯的平均涌出量，m3/min。

1.4 数值模拟及结果分析

不借助任何通风设备，模拟自然条件下原煤仓的瓦斯运移情况。根据铁东选煤厂所处环境的年平均气温变化，得到该地区夏季室外平均气温为20 ℃，该温度下原煤仓内瓦斯浓度(CH4体积分数，下同)的模拟结果见图2。

图2 20 ℃时原煤仓内瓦斯浓度分布三维云图

该地区冬夏两季室外平均气温温差较大，冬季室外的平均气温为-20 ℃，该温度下原煤仓内瓦斯浓度的模拟结果见图3。

图3 -20 ℃时原煤仓内瓦斯浓度分布三维云图

由图3可知，根据原煤仓内瓦斯浓度，由上至下可将原煤仓划分为4个区域：中空区、自然堆积区、亚压实区、压实稳定区。其中中空区位于原煤仓顶部至下方10 m处，该区域为流体流动区域，区域内气体成分为瓦斯和空气；自然堆积区位于中空区下方边缘处至其下方3 m处，该区域煤体相对松散，在整个煤体中孔隙率最大，瓦斯在该区域的上升过程中阻力最小，因此该区域内瓦斯浓度相对较低。随着原煤仓内煤体体积增加，煤体间的缝隙减小，煤体释放的瓦斯不能迅速扩散，会在仓底积聚，所以在整个原煤仓内仓底处的瓦斯浓度是最高的。

由图2、图3可知，在冬季原煤仓中空区的瓦斯浓度大于3.0%，而夏季瓦斯浓度大于4.0%，位于原煤仓内底部储煤区域的瓦斯浓度大于5.0%。瓦斯浓度在中空区呈线性变化，该区域内瓦斯浓度与原煤仓高度呈正比关系，而该变化关系仅适用于原煤仓体内部，而在通风口处的瓦斯浓度比同高度原煤仓内部的瓦斯浓度低，在整个原煤仓内瓦斯浓度最低，约为3.2%。

根据上述模拟结果，对照《煤矿安全规程》(以下简称“规程”)[16]，该原煤仓内中空区内的瓦斯浓度已超过规程限定值(1%)，表明该原煤仓上方非煤区域内瓦斯浓度明显超标。因此可判定该原煤仓处于瓦斯超限状态，该选煤厂存在安全隐患。

1.5 实测数据对比

采用瓦斯浓度传感器对原煤仓中空区的瓦斯浓度进行实时监测，传感器安装于胶带支架上，瓦斯浓度传感器布置如图4所示。

图4 瓦斯浓度传感器平面布置图

为验证数值模拟结果的准确性，将改造前原煤仓内瓦斯浓度变化的实时监测数据(2017年7月 25日)与数值模拟结果进行对比，绘制出瓦斯浓度随时间变化的对比图，如图5所示。

图5 瓦斯浓度随时间变化对比图

模拟所得该原煤仓中空区夏季的瓦斯浓度为3.6%，而实际监测数据显示该区域的瓦斯浓度在3.6%上下波动，二者结果基本一致，表明本文采用的数值模拟方法是准确的。

2 选煤厂原煤仓瓦斯超限治理方案

模拟结果及实测结果表明该选煤厂原煤仓的瓦斯超标情况较严重，需要对原煤仓采取措施，以满足规程要求。笔者从安全和经济的角度出发，通过增加原煤仓通风口的数量,以及仓外通风设施对原煤仓进行优化改造，采用4种优化方案并进行模拟，通过对比和分析，选取最优的解决方案，以解决该原煤仓瓦斯超限的问题。

2.1 一进两出、正压通风可行性分析

1)方案1：正压通风，风速为1.0 m/s。

在原煤仓现有结构的基础上，添加风机，向煤仓内进行正压通风，风速为1.0 m/s。两侧窗体结构为风流的自由出口，将煤仓内的预混气体排出煤仓体，降低煤仓内的瓦斯浓度。该模拟过程中环境温度为20 ℃，模拟结果如图6～8所示。

图6 正压风速1.0 m/s时原煤仓瓦斯浓度分布三维云图

图7 正压风速1.0 m/s时原煤仓z=38 m位置速度矢量图

图8 正压风速1.0 m/s时原煤仓z=35 m位置速度矢量图

由图6可知，通风过程中原煤仓仓底的瓦斯浓度小于2.4%，而中空区的瓦斯浓度为1.2%，部分区域的瓦斯浓度仍然超过规程限定的数值。

由图7、图8可知，在35 m以上区域存在局部阻力，因此产生了两处涡流，瓦斯在该区域出现了积聚现象，因此方案1无法解决原煤仓瓦斯超限的问题。

2)方案2：正压通风，风速为1.6 m/s。

不改变方案1的边界条件，只增大进口处的风流速度，将风速提高至1.6 m/s，模拟结果如图9 所示。

图9 正压风速1.6 m/s时原煤仓瓦斯浓度分布三维云图

由图9可知，方案2未能改变压实稳定区的瓦斯浓度，因此压实稳定区瓦斯浓度小于3.0%；而中空区的瓦斯浓度降低至0.8%，表明原煤仓内瓦斯浓度处于安全生产规程范围内。

通过对比方案1、2的模拟结果可知，方案2符合安全生产规程。由于低风量能降低煤仓内煤与氧气发生氧化反应的概率，也会减少煤的风化过程，因此需提出减小风量的方案，以达到安全生产要求。

2.2 两进两出、正压通风可行性分析

在原煤仓现有结构的基础上，增加煤仓通风口的数量，使其通风方式为对称通风，同时增加通风机数量，每个通风机对应一个通风出口。

1)方案3：正压通风，风速为0.5 m/s。

新的物理模型的网格划分方式与原物理模型一致，如图10所示。将2个进口的风速均设置为 0.5 m/s，模拟结果如图11～13所示。

图10 原煤仓网格划分图Ⅱ

图11 正压风速0.5 m/s时原煤仓内瓦斯浓度分布三维云图

图12 正压风速0.5 m/s时原煤仓内z=38 m位置速度矢量图

图13 正压风速0.5 m/s时原煤仓内z=35 m位置速度矢量图

由图11可知，储煤区是原煤仓中瓦斯浓度最高的区域，该区域瓦斯浓度为2.0%，原煤仓的瓦斯浓度由上至下逐渐减小，煤体上部与空气接触的部位瓦斯浓度最低为1.2%；中空区部分瓦斯浓度虽略有差别，但总体不超过1.0%，进风口处是瓦斯浓度最高的区域，瓦斯浓度大于1.0%。

由图12、图13可知，中空区的阻力较小，没有产生明显的气流涡旋，导致进风口区域之间瓦斯浓度略高的原因是类似于风流经过障碍物后速度减小导致微风区效应的产生，这部分区域气体的流动较缓慢，聚积的瓦斯不能快速被风流稀释排出煤仓外。

2)方案4：正压通风，风速为0.7 m/s。

在方案3的基础上增大风流速度，每个进风口的风流速度增加至0.7 m/s，模拟结果如图14～16所示。

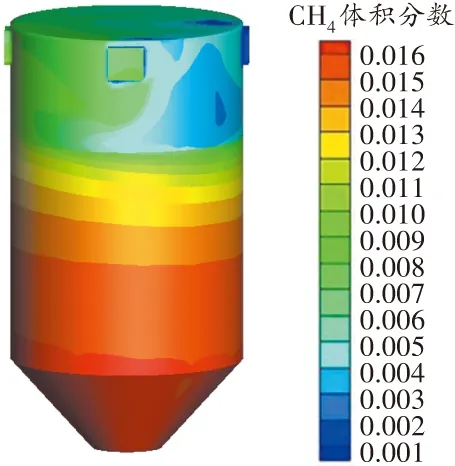
图14 正压风速0.7 m/s时原煤仓内瓦斯浓度分布三维云图

图15 正压风速0.7 m/s时原煤仓内z=38 m位置速度矢量图

图16 正压风速0.7 m/s时原煤仓内z=35 m位置速度矢量图

由图14可知，原煤仓中瓦斯浓度最高值为1.6%，煤仓内瓦斯浓度基本符合安全生产规程要求，中空区的瓦斯浓度小于1.0%。

由图15、图16可知，在该通风方式下，煤仓内局部阻力较小，中空区不存在气流涡旋现象，风流分布较为均匀。

方案4是理论上最为理想的优化方式，既降低了中空区的瓦斯浓度，又使煤仓内煤体的瓦斯浓度符合规程规定值、进风量减少，所以该方案为治理原煤仓瓦斯超限的最优方案。

2.3 煤仓风量需求确定

在夏季通风过程中，方案4所需的最大风量Q=756 m3/min。在冬季煤体瓦斯的释放速度较缓，可降低通风需求，采用方案4的边界条件对-20 ℃时的原煤仓进行数值模拟研究，设置进口风速为0.5、0.6 m/s。模拟结果如图17～18所示。

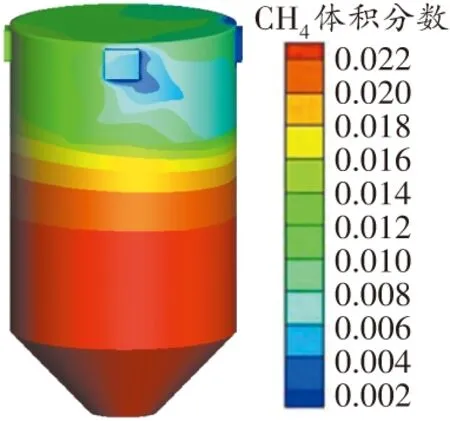
图17 冬季风速0.5 m/s时原煤仓内瓦斯浓度分布三维云图

由图17、图18可知，当风速为0.5 m/s时可以满足压实稳定区的瓦斯浓度要求，但中空区的瓦斯浓度超标；当风速为0.6 m/s时，原煤仓各处的瓦斯浓度均符合安全生产要求。

通过模拟可知，原煤仓处于-20 ℃低温环境时，通风量要小于20 ℃正常室温时的通风量，该条件下所需通风量Q为648 m3/min。

3 结论

1)通过建立原煤仓的物理模型，采用数值模拟方法得到原煤仓内瓦斯的分布状态，瓦斯浓度呈梯度分布，自上至下逐渐增高，由上至下可将原煤仓划分为4个区域，即中空区、自然堆积区、亚压实区、压实稳定区，从储煤区域涌出的瓦斯会聚积在原煤仓顶部的中空区。

2)对选煤厂原煤仓数值模拟结果及现场实测数据进行对比分析，验证了数值模拟结果和数值模拟手段的准确性。

3)增加通风口数量，形成进出比例相同的通风系统，根据室外温度的不同，定义不同的进风速度，根据安全生产规程规定的原煤仓瓦斯浓度得到冬夏两季的进风速度为0.7、0.6 m/s。