灯盏花挥发性组分结构与保留时间关系研究

李建凤，廖立敏*

1内江师范学院化学化工学院；2“果类废弃物资源化”四川省高等学校重点实验室，内江 641100

灯盏花是菊科植物短葶飞蓬(Erigeronbreviscapus)的全草，又名灯盏细辛、东菊[1]。灯盏花主要生长在我国云南、广西、四川、贵州、西藏等高海拔地区。灯盏花性寒、微苦、甘温辛，具有散寒解表、祛风除湿、活血化瘀、通经活络、消炎止痛等功效[2]。目前，灯盏花在临床上主要用于心脑血管疾病、糖尿病、肾病和眩晕等疾病的治疗。Xu等[3]利用固相微萃取、气相色谱-质谱联用技术对灯盏花中的挥发性成分进行了定性分析。化合物结构与色谱保留时间关系研究，对于分析化合物的色谱保留行为、辅助鉴定化合物等具有重要的意义[4]。化合物结构参数化表征是建立化合物结构与性质关系的关键步骤之一，目前研究者在这方面做过许多工作，如He等[5,6]利用分子连接性指数和分子拓扑指数对果酒、香水百合头中部分挥发性成分进行了结构-保留关系研究，Zhang等[7]利用分子连接性指数对燃料油中有机硫化物进行了结构-保留关系研究，均取得较好的结果。分子连接性指数和分子拓扑指数都属于分子二维结构描述符，它的优点就是计算快速、简便、易懂，缺点是不能区分顺反异构、光学异构等现象；又如Jing等[8]利用三维全息原子场作用矢量对部分脂肪酸进行了结构-保留关系研究，Liu等[9]利用化合物三维结构计算结构参数值对饱和醇类化合物进行了结构-保留关系研究，均取得较好的结果。分子三维结构描述符，它的优点就是基于化合物分子三维立体结构计算，更加接近化合物分子实际存在的状态，可以区分顺反异构、光学异构等现象，缺点是需要进行分子结构优化、计算复杂、难懂、工作量大，有时还可能涉及到探针选取、网格划分、分子重叠等不确定因素[10]。本文在前人的基础上构建新的二维结构描述符，对灯盏花中出现的多类有机化合物进行结构表征，进而运用多元线性回归(MLR)和偏最小二乘回归(PLS)两种方法建立化合物结构与保留时间关系模型，分析影响化合物色谱保留时间的结构因素，为挥发性化合物结构-性质关系研究提供参考。

1 材料和方法

1.1 实验材料

以灯盏花中的64种挥发性有机化合物为研究样本，化合物保留时间是以HP-5 ms(30 m×250 μm×0.25 μm)为色谱柱分离得到，柱箱升温程序为：初始温度50 ℃，保持1 min，以5 ℃/min升至220 ℃保持6 min，再以10 ℃/min升至260 ℃保持15 min。进样口温度280 ℃。采用脉冲不分流进样模式。载气使用高纯氦气，流速为1.0 mL/min。按照色谱保留时间(tR)[3]大小顺序列于表1，取序号个位数为“0”和“5”的化合物(用“*”标注，共12个)为测试样本集，测试样本集不参与建模，仅用于评价模型的外部预测能力，其余52个化合物为训练样本集用于建立模型。

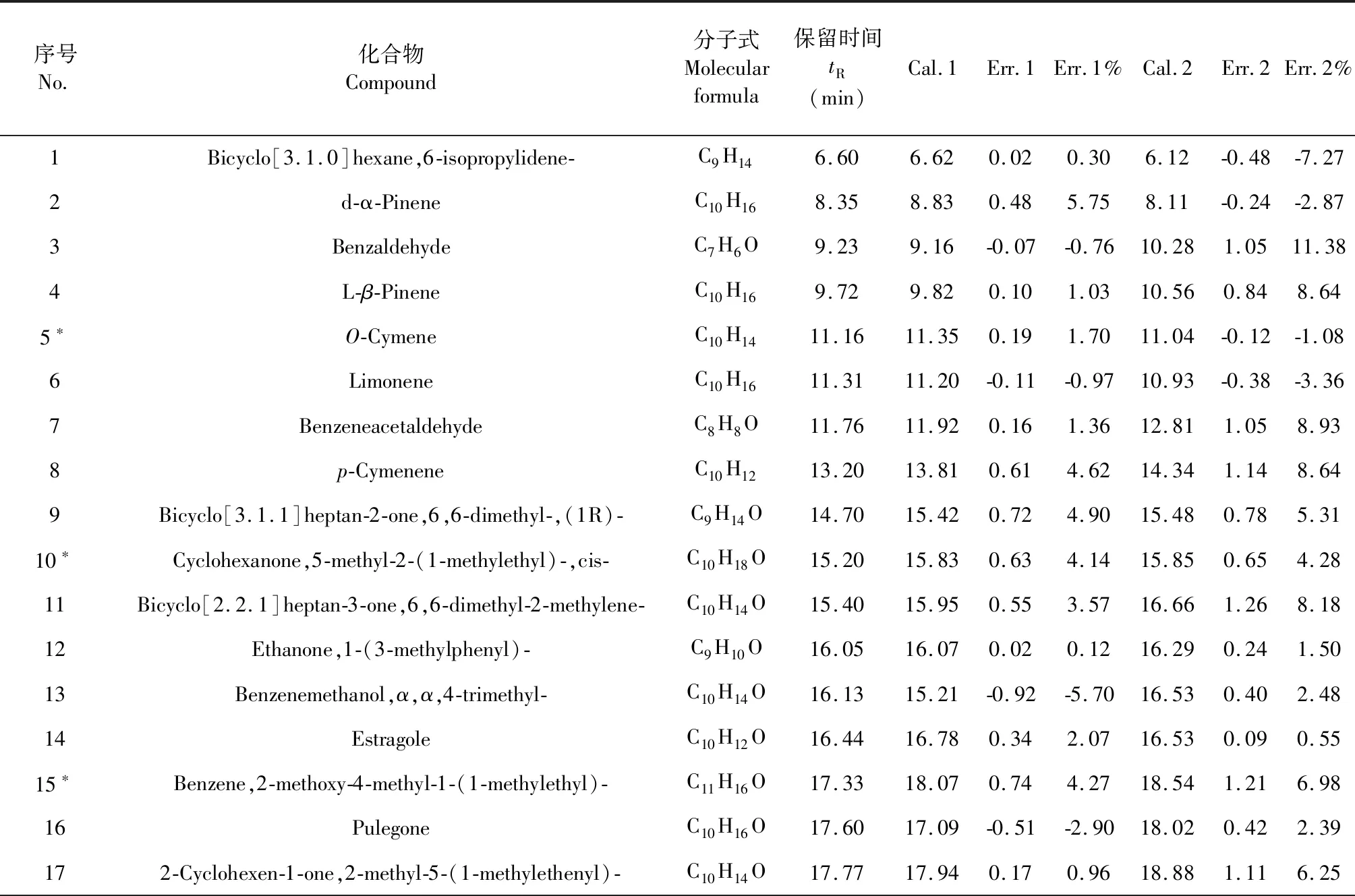
表1 64种挥发性有机化合物及其色谱保留时间Table 1 64 volatile organic compounds and their chromatographic retention times

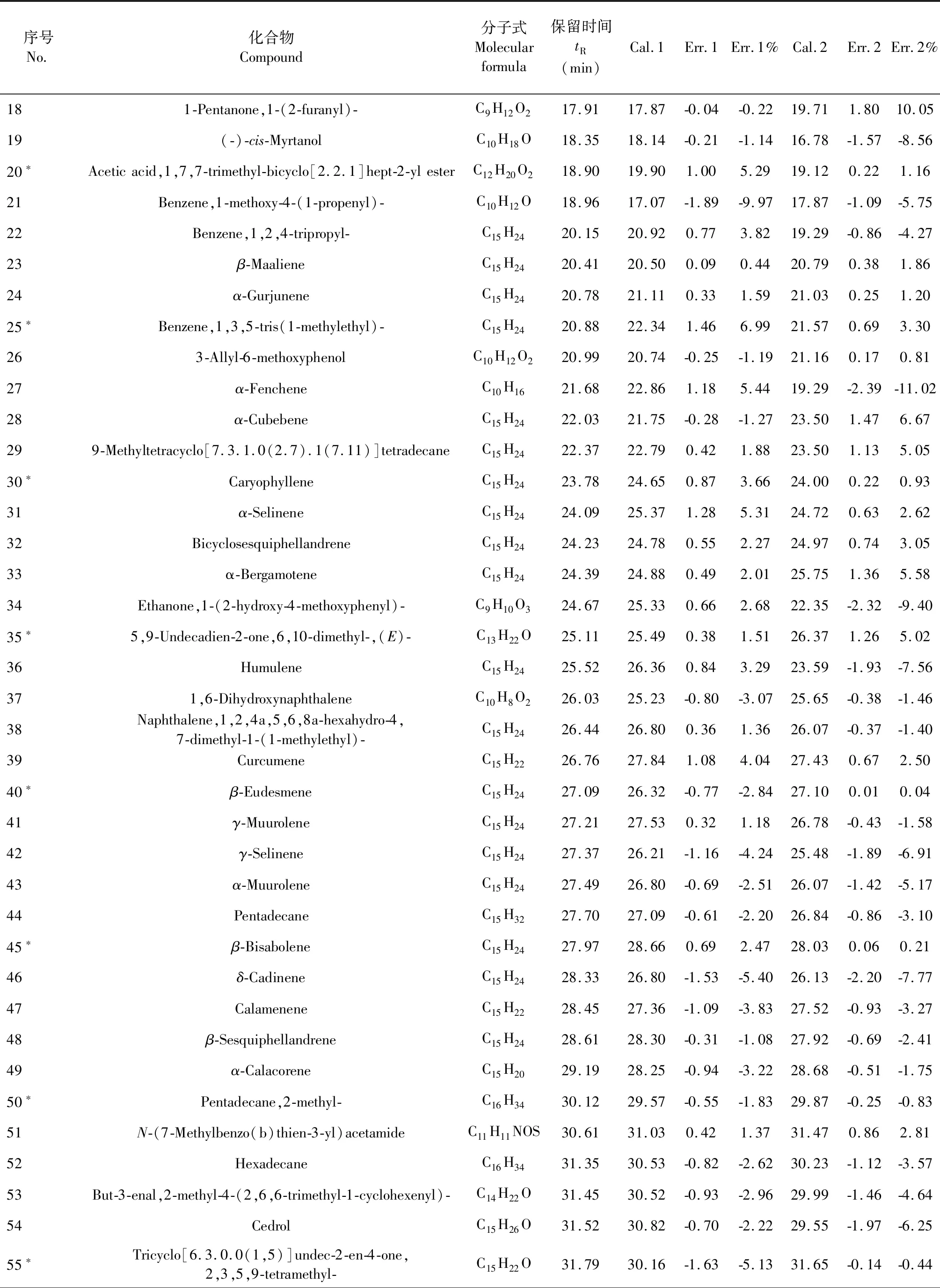
续表1(Continued Tab.1)

续表1(Continued Tab.1)

多元线性回归使用的是SPSS13.0软件、偏最小二乘回归使用的是SIMCA-P 11.5软件。

1.2 实验方法

1.2.1 化合物分子结构表征

构建化合物结构与性质之间的关系模型，化合物结构参数化表征是关键步骤之一。认为化合物中的非氢原子以及它们之间的关系对化合物色谱保留时间产生影响，而氢原子影响通常被忽略。不同类型的非氢原子以及不同类型非氢原子之间的关系对化合物色谱保留时间影响不同，参照文献[11-13]方法将化合物中的非氢原子按照其连接的其它非氢原子数分为4类，与k个其它非氢原子相连的非氢原子属于第k类非氢原子，例如与2个其它非氢原子相连的仲碳原子属于第2类非氢原子。在参考文献[14-16]的基础上，对化合物中的非氢原子进行参数化染色，见式(1)。

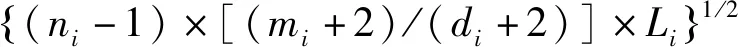
(1)

式中i为非氢原子在分子中的编码；ni为非氢原子i的原子核外电子层数；mi为价电子数，di为非氢原子i的成键电子数，也就是氧化数；Li为非氢原子i与相邻非氢原子直接连接的化学键数(δ键取值为1，π键取值为0.5)。非氢原子i的ni越大，其半径就越大，相应的原子体积就越大，相应的Zi值也就越大。

非氢原子自身对化合物色谱保留时间的影响，按照式(2)进行分类累加。

(2)

式中，k表示非氢原子i的原子类型，Zi按式(1)计算。根据非氢原子的分类，对于一个有机化合物分子中最多含有4类非氢原子，因此最终可得到4个非氢原子自身对化合物保留时间的影响项，用x1、x2、x3和x4表示。

4类非氢原子之间可以有10种不同的组合，即m11、m12、…、m44，简写为x5、x6、…、x14，m13表示第1类非氢原子与第3类非氢原子之间的关系，以此类推。非氢原子之间的关系并非某种具体的相互作用，而是要反映出相关程度随着非氢原子间的距离的增大而减小，随着非氢原子自身某种性质的增大而增大，式(3)可以满足此要求。

(n=1，2，3，4；n≤l≤4)

(3)

Z按式(1)计算；dij为非氢原子i、j之间的相对距离(即键长之和与碳碳单键键长的比值，如果i、j之间有多条路径，则以最短的为准)；n和l为原子所属类型，α=0.5。这样一来，对于一个化合物经参数化表达后最多可得14个变量(结构描述符)。

1.2.2 建模与评价

(4)

(5)

2 结果与讨论

2.1 分子结构表征

化合物经分子结构表征后得到14个变量，由于变量数较多，在此没有全部列出。部分用到的变量列于表2。

表2 化合物的结构参数化表征结果Table 2 Structural parameterized characterization results of compounds

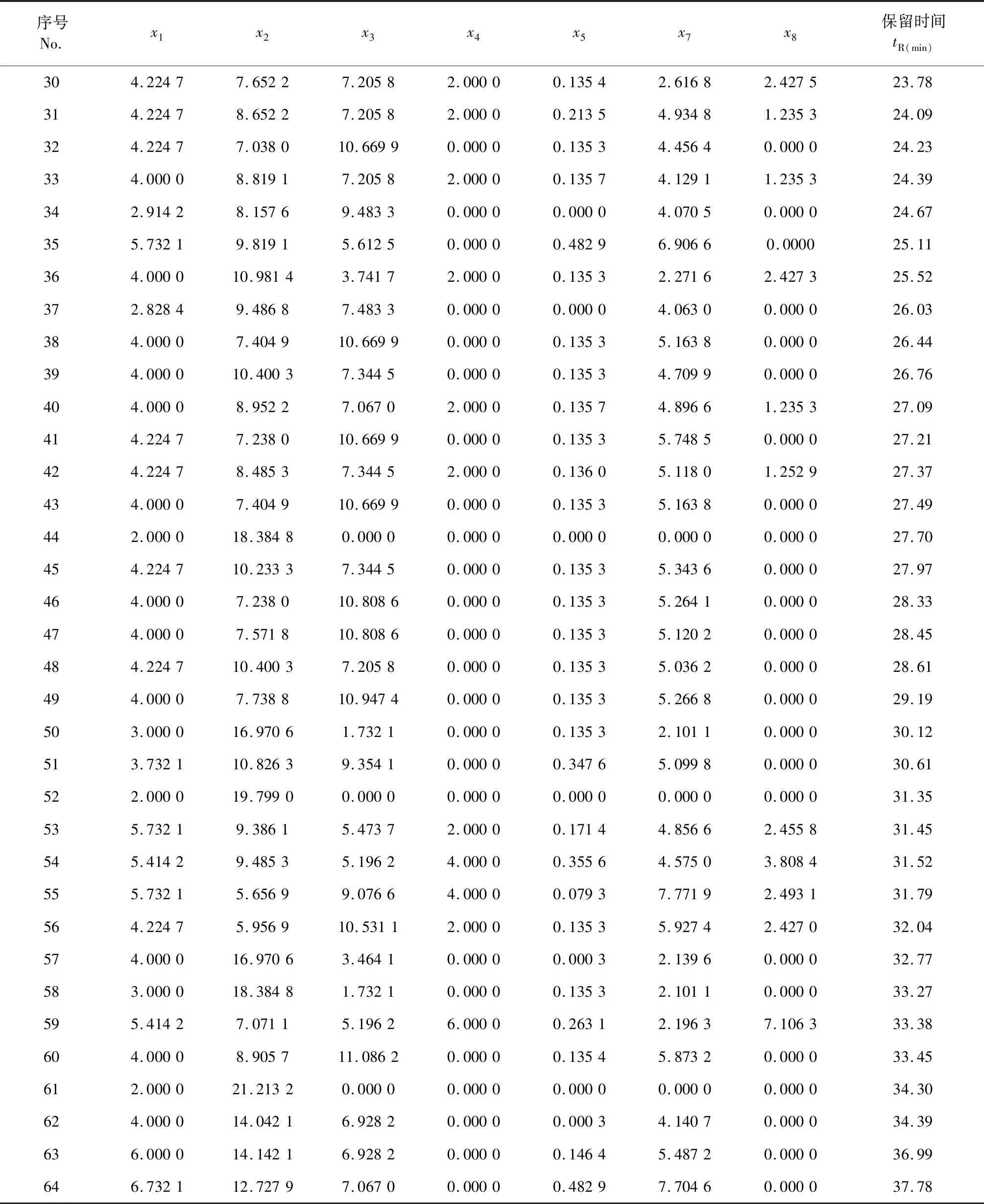
续表2(Continued Tab.2)

2.2 化合物结构与色谱保留关系

2.2.1 多元线性回归模型

本研究的训练集样本数为52个，而变量数多达14个，不符合N/n≥5的经验规则，因而在确定最优模型之前应该对变量进行筛选，将与化合物色谱保留时间(tR)相关性不大的变量进行剔除。逐步回归(SMR)是筛选变量的常用方法，建模前运用逐步回归依据变量显著性大小顺序逐步引入候选变量，根据每一步所得模型的相关系数(R2)及标准偏差(SD)进行综合考量后选出最佳变量组合进行回归建模。对选定的模型变量间的共线性进行评价，计算方差膨胀因子(VIF)，如果某变量的方差膨胀因子(VIF)大于或等于20，则应减少变量建模。在逐步回归中，相关系数(R2)和标准偏差(SD)随变量的引入而发生变化，为便于直观分析将其变化情况绘图于图1及图2中。

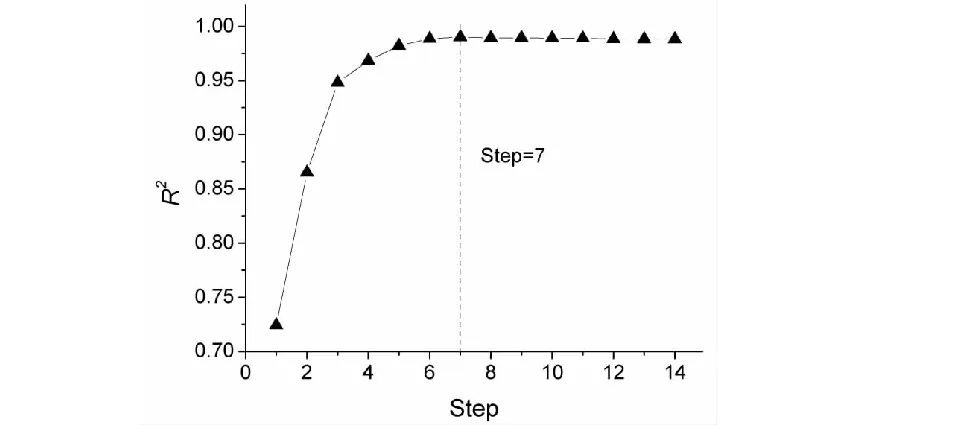
图1 R2在逐步回归中的变化情况Fig.1 Changes of R2 in stepwise regression

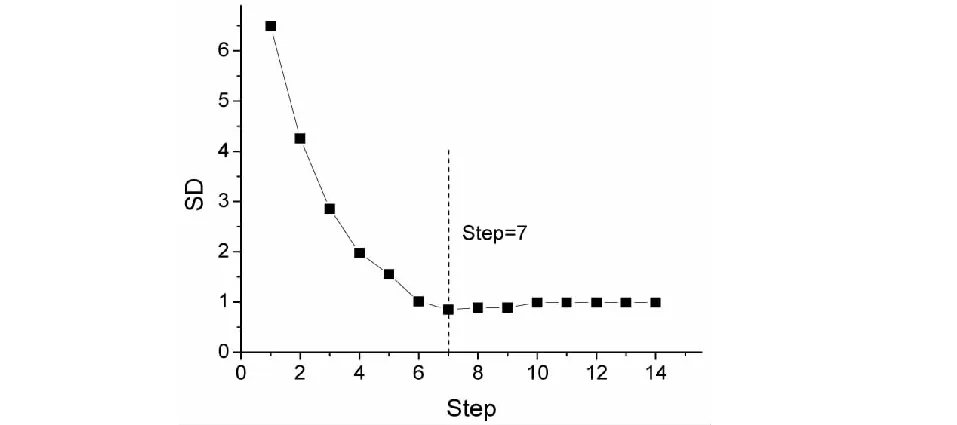
图2 SD在逐步回归中的变化情况Fig.2 Changes of SD in stepwise regression

从图1中可以发现，相关系数(R2)随着变量的引入而增大，起初增大的趋势明显，当逐步回归进行到第7步时相关系数(R2)接近最大值，之后相关系数(R2)增大趋势放缓。同样，图2中可以发现，标准偏差(SD)随着变量的引入而逐渐减小，起初减小的趋势明显，当逐步回归进行到第7步时标准偏差(SD)达到最小值，之后标准偏差(SD)略有增大。对7变量模型进行回归诊断，发现变量x8的方差膨胀因子(VIF)最大，且值仅为13.045 2，变量之间没有明显的共线性。当变量继续引入，逐步回归进行到第8步，虽然相关系数(R2)略有增大，然而此时最大变量方差膨胀因子(VIF)远大于20，说明8变量模型不可靠。综合各方面的考量后，认为应该选择逐步回归第7步所得变量组合(x1、x2、x3、x4、x5、x7、x8，列入表2)进行建模(M1)，如式(6)。

tR= -18.629 3+0.479 4×x1+2.434 4×x2+1.640 6×x3

-1.601 5×x4-8.006 6×x5+1.755 8×x7+4.322 7×x8(6)

2.2.2 偏最小二乘回归模型

偏最小二乘回归(PLS)也是化合物结构和性质关系研究中常用的方法之一，特别适合于样本数较少而变量数较多的情况下建模。变量x1、x2、x3、...x14作为自变量X，化合物色谱保留时间(tR)作为因变量Y，建立偏最小二乘回归模型(M2)。相关系数(R2)及交互检验的相关系数(RCV2)随主成分数(A)的变化情况见图3。图3中可以看出当主成分数(A)达到6个时，相关系数(R2)接近最大值，交互检验的相关系数(RCV2)达到最大值，应该选择6个主成分进行建模(M2)。52个训练集样本在PLS前2个主成分得分空间散点分布绘于图4，图4中可以发现全部样本得分点都落在95%置信度的椭圆置信圈内，没有出现一个异常点，反映出构建的结构描述符能较好地表现挥发性有机化合物的分子结构特征，并在统计模型中得到正确的表现。

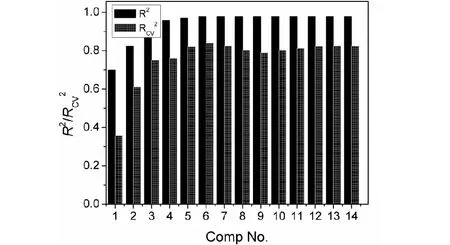
图3 相关系数随主成分数的变化情况Fig.3 Correlation coefficient change with the number of principal components

图4 样本在前2个主成分得分分布Fig.4 Distribution of the top 2 principal component scores of the sample

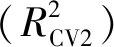
为验证模型结果是否为偶然所得，对模型进行20次Y向量随机排序验证。以Y原始向量和经过随机排序的Y向量相关系数对模型的R2和RCV2作图于图5。根据Andersson等[20]提出的判断标准，R2和RCV2在纵轴上的截距分别不得超过0.300和0.050。从图5中可以发现所建PLS模型的R2和RCV2的截距分别为0.105和-0.882，因而认为模型的优良结果并非偶然，偏最小二乘回归模型(M2)可以用于分析化合物结构对色谱保留时间的影响。

图5 Y向量随机排序验证结果Fig.5 Y vector random sorting verification results

变量重要性可以反映出变量与Y之间的相关程度，通常认为变量重要性投影(VIP)值大于1的变量与化合物色谱保留时间(tR)相关性大。变量重要性投影见图6，图6可以看出变量x2、x1、x9这3个变量的VIP值大于1，说明这3个变量与化合物色谱保留时间(tR)相关性大。x1、x2分别为第1、2类非氢原子自身对化合物色谱保留时间的影响，x9为第2类非氢原子之间的关系对化合物色谱保留时间的影响。第1类非氢原子对应取代基的末端原子，而第2类非氢原子的多少决定了链的长度，说明化合物支链越多、链越长，即伯、仲碳原子越多，化合物可能具有较大的色谱保留时间(tR)值，这与表1中的数据特征基本吻合。

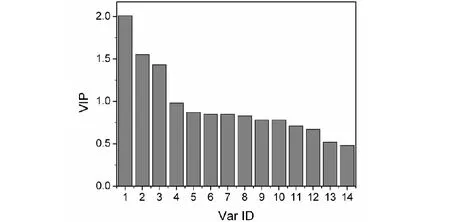
图6 变量重要性投影图Fig.6 Projection of variable importance

2.2.3 模型结果与比较

多元线性回归(MLR)模型(M1)和偏最小二乘回归(PLS)模型(M2)对训练集化合物的色谱保留时间进行了计算，对不参与建模的预测集化合物色谱保留时间进行了预测，M1和M2对化合物的计算值及预测值分别列于表1的Cal.1和Cal.2列，Err.1和Err.2分别为误差，Err.1%、Err.2%分别为百分误差。两模型对化合物保留时间的计算值与实验值相关性，见图7。图7中容易看出所有样本点都落在正方形45°对角线附近，说明两模型对化合物保留时间计算值与实验值相关性好，两者间误差不大。另外，图上可以看出Cal.1的样本点与Cal.2的样本点分布大体相似，说明模型(M1)与模型(M2)的质量大体相当。

图7 模型预测值与实验值的相关图Fig.7 Correlation diagram between model predicted values and experimental values

模型对化合物保留时间计算值的误差可以反映模型预测的准确性，两模型计算误差分布见图8。图8中可以发现大部分样本的预测误差值都处于2倍标准偏差(±2SD)范围以内，对于模型(M1)、模型(M2)均仅有2个化合物(3.13%)超出±2SD1、±2SD2，说明两模型对化合物保留时间预测较为准确，误差都处于可以接受的范围内。另外，绝大多数样本的Err.1小于Err.2，±2SD1线处于±2SD2线内侧并更加靠近中的“0”线，说明模型(M1)的质量略优于模型(M2)。

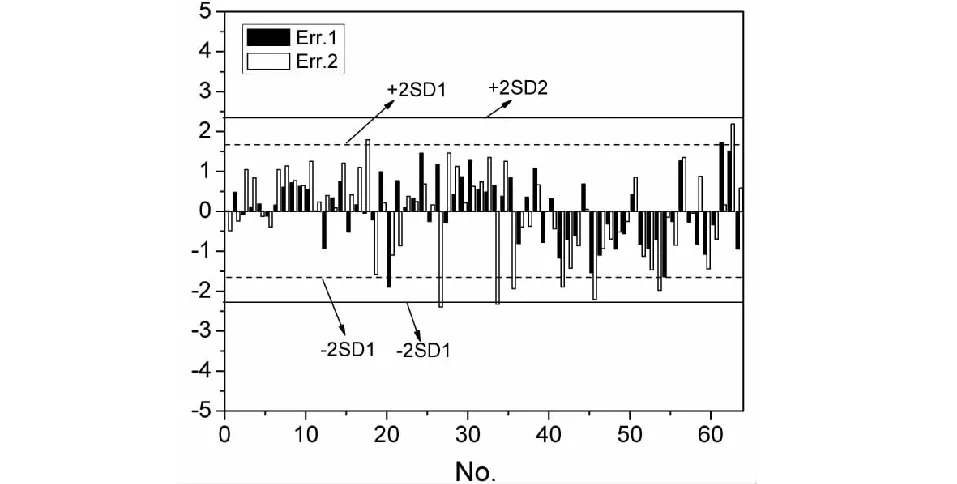
图8 模型对样本保留时间预测误差Fig.8 Model prediction error of samples′ tR

本文所研究的化合物结构跨度大，包括了33种烃类、9种酮类、8种芳香族类、4种醇类、3种醛类、3种醚类、2种酚类和2种酸类等类型化合物，含有氧、硫、氮等杂原子，含有单键、双键、三元环、四元环、五元环、六元环、七元环、八元环、十一元环等结构，说明构建的结构描述符普适性强。对于复杂样本体系的定量结构与保留时间关系研究已有一些报道，为便于对比，现将本文结果与部分文献结果列于表3，可以发现本文所取得的结果明显优于文献。

表3 模型比较Table 3 Comparisons among different QSRR models

3 结论

通过构建非氢原子之间的关系得到新的结构描述符，对灯盏花中的64种挥发性有机化合物结构进行了参数化表征，运用多元线性回归(MLR)和偏最小二乘回归(PLS)方法构建了化合物结构与色谱保留时间的关系模型。经检验模型具有通良好的拟合能力、稳定性和外部预测能力。分析了影响化合物色谱保留时间的结构因素，结果表明化合物的伯、仲碳原子越多，色谱保留时间(tR)值就越大。构建的化合物结构描述符为二维结构描述符，计算简便、快速、易懂、通用性强，对于化合物结构与性质关系研究具有一定的参考价值。