基于遗传算法的词语语义相似度计算研究

杨 泉

(北京师范大学，北京 100875)

0 引 言

语义相似度是对给定的语言对象间语义相似程度的衡量，通常用[0,1]之间的数值来表示。语义相似度计算就是计算语义相似度具体数值的过程。语义相似度计算对象的层级可分为词、短语、句子、篇章，该文主要研究词层级上两个词之间的语义相似度计算问题。

语义相似度计算目前在机器翻译、人机问答、情感计算、信息提取等很多领域中都有着广泛的应用[1]。语义相似度计算方法主要分为两类：一类是在大规模语料的基础上直接统计和计算的方法；另一类是根据某种已有知识本体(ontology)或分类体系(taxonomy)来计算的方法[2-3]。基于语料库的方法对语料的依赖性较大，需要在大规模精确标注语料的基础上进行，但语料的规模、内容、范围以及标注的标准和规范难以统一，而且可解释性较差；而基于知识本体或分类体系的方法在这些方面就显示出了其优越性，越来越多的专家学者都进行了有效的尝试。

用于语义相似度计算的汉语知识本体目前主要有《知网》[4]和《同义词词林》[5]。前人研究中有很多利用《知网》的树状结构或概念义原来进行语义相似度计算，如文献[6]介绍了一种基于《知网》树状结构的语义相似度计算方法；文献[7]在综合考虑《知网》义原距离、义原深度、义原宽度、义原密度和义原重合度的基础上，利用多特征结合的方法计算词语相似度；文献[8]基于对《知网》中词语、义项和义原三个层次概念的研究，针对词语相似度计算中结果合理性的问题，提出了一种结合信息论研究中熵的概念的新的词语相似度计算方法。但是与《知网》相比较而言，《同义词词林》内部结构比较清楚，可以较为容易地转化成树形图来计算词语的深度和路径，国内也有很多研究人员利用《同义词词林》计算词语之间的语义相似度，文献[6,9]利用《词林》的编码及结构特点，结合词语的相似性和相关性，计算语义相似度。文献[10]提出了一种综合《知网》与《同义词词林》的计算方法。《词林》部分采用以词语距离为主要因素、分支节点数和分支间隔数为微调节参数的方法计算语义相似度。文献[11]根据《词林》提出了一种基于路径与深度的算法。该方法通过两个词语义项之间的最短路径以及它们的最近公共父节点在层次树中的深度计算出两个词语义项之间的相似度。在计算过程中为分类树中不同层之间的边赋予不同的权值，同时通过两个义项在其最近公共父节点中的分支间距动态调节词语义项间的最短路径。文献[12]提出了一种基于路径与《同义词词林》编码相结合的语义相似度计算方法。该方法认为《词林》编码体系是按从左到右依次递增的关系排列分支，距离越近的概念分支间隔越小，编码距离也越近，由此根据每个分类节点下面的分支节点顺序及编码规律设计了计算模型。

以上这些模型都是根据经验建立语义相似度的函数表达式，主要从两个方面提高计算语义相似度的准确性：一是如何使用知识本体中的知识并进行量化；二是如何选择更合适的函数表达式。由于《同义词词林》的内部结构清晰简洁，使用深度、距离和节点分支数作为基础知识进行相似度计算已经成为共识。因此如何突破已有经验的局限性，寻找并建立更加合理的相似度函数表达式是进一步完善基于《同义词词林》的语义相似度计算方法的主要途径。

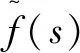
1 《同义词词林》简介

《同义词词林》是梅家驹等人1983年编撰的可计算汉语词库，后经哈工大信息检索研究室扩展编辑为《哈工大信息检索研究室同义词词林扩展版》(下文简称《词林》)。经统计《词林》共有77 456条词语，分为12个大类；95个中类；1 428个小类；4 026个词群和17 817个原子词群。前面四个层级的节点都代表词语的类别，第五层叶子节点上是原子词群，每个原子词群可用一个8位编码唯一表示。表1展示了《词林》中的义项编码。

表1 《词林》义项编码

第八位编码只有三种情况：其中“=”代表“相等、同义”关系；“#”代表“不等、同类”关系；“@”代表“唯一、独立”关系。前七位编码确定后就可以唯一确定一条编码，不存在前七位编码相同而第八位不同的情况。

在大类中A、B、C类多为名词，D类多为数词和量词，E类多为形容词，F、G、H、I、J类多为动词，K类多为虚词，L类是难以被分到上述类别中的一些词语，各大类编码具体含义如表2所示。

表2 《词林》大类编码含义

《词林》结构安排中大类和中类的排序遵照从具体到抽象的原则[5]，每个大类都可以转化为一个树形结构图，比如E大类下面分为6个中类，从“外形”到“境况”，详见图1。

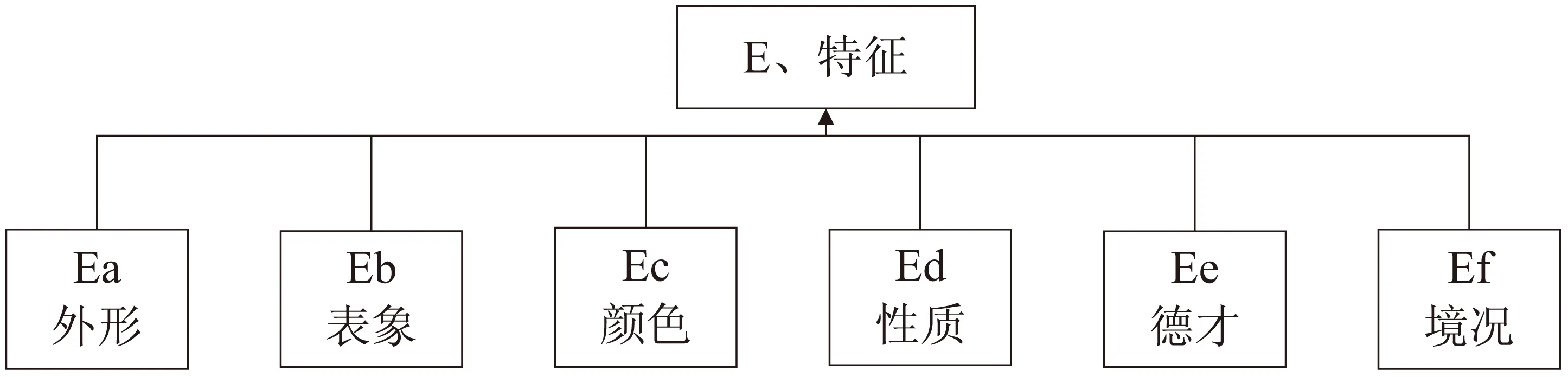
图1 《词林》E大类语义场

通过上文对《词林》整体架构的分析，其义项编码可以直接映射为一个树形结构图，所有的词语都可以对应到叶子节点的词群里。实际上这个树形结构图就是使用的知识本体，而每个知识本体反映的都是作者对于世界知识的认识，语义相似性是世界知识很重要的一个组成部分，作者在编著《同义词词林》时就已经融入了语义相似信息，只是没有把这种相似性信息数量化、数值化。因此基于《词林》的两个词语之间的语义相似度计算，实际上就是解析蕴含于知识本体中的语义相似信息，将其形式化后转化为可计算的函数表达式，最终计算出量化的数值。

2 基于遗传算法的语义相似度计算模型

表1说明《词林》中共有五个层级，为便于计算，该文在第一层级上面再引入一个虚拟层级，称为第0层，对应树形结构图中的根节点，记为R。在此情况下《词林》共有六层节点、五层边，所有词语都落在树形结构图最底层的叶子节点上，所有叶子节点都是一个原子词群。在该树形结构中将两个节点之间最小的边数称为两个节点之间的路径长度或距离。将各非根节点到根节点R的距离称为该节点的深度。

计算语义编码分别对应不同的叶子节点的词语s1与s2的语义相似度S，根据《词林》编码规则，这两个词语在其最近公共父节点处分离，分属不同类别。将其公共父节点记为F，将F的深度记为D。从《词林》体系中可以直观地看出，F在《词林》体系中所处层级越高，则D的取值越小，此时s1与s2分离得越早，相似度就低；相反F在《词林》中所处层级越低，D的取值越大，则s1和s2分开得越晚，其相似度就高。因此D的取值与S成正比关系；而F的位置与S成反比关系。这从语言学角度也很容易理解，当两个词语所处的分支层的公共父节点越低，说明这两个词语所在的类别距离越近，两个词语的语义相似程度就越高；相反当两个词语所处的分支层的公共父节点越高，说明这两个词语所在的类别距离越远，两个词语的语义相似程度就越低。上述分析表明在《词林》所表示的知识本体中，两个词语s1与s2的最近公共父节点的深度对其相似度起决定性作用。例如“我们”的语义编码为“Aa02B01=”，“你”的语义编码为“Aa03A01=”，“消毒剂”的语义编码为“Br13D04#”。“我们”与“你”的语义类别在同一个大类A中，而“我们”与“消毒剂”的语义类别分别在A和B两个大类中，因此前两者的语义相似度一定高于后两者。

在树形结构中还常用两个节点间的路径长度H来表示两个节点之间的关系。任意两个叶子节点之间的路径长度H就是它们到其最近公共父节点路径长度之和，根据《词林》中树形结构的特点：所有叶子节点到根节点R的路径长度相同，在此记为常数C；叶子节点到其公共父节点的路径长度也相同。而叶子节点到根节点的路径长度等于叶子节点到其任意父节点的路径长度与该父节点到根节点路径长度之和。由此可以得出路径长度与深度之间的关系式：

(1)

该结论说明路径长度和深度是两个能够相互表示的量，该文在计算相似度时选择将深度作为主要因素。文献[2]在总结基于WordNet的英语语义相似度计算方法中有一类使用路径和深度的计算方法，但由于WordNet与《词林》的组织架构不同，在WordNet中不同的词语可能具有不同的深度，这种叶子节点深度不均匀，义项遍布所有节点的组织方式与《词林》是截然不同的。

在《词林》体系中，词语按照类别逐级细分，在同一个类别中的排序遵照从具体到抽象的原则进行排列(如图1所示)。这说明在同一个类别层级中，意思接近的两个分类其排列的位置也会接近，对应到树形结构中，就是在同一个节点上排列的分支中，离得越近的分支其代表的意思也越接近。因此词语s1与s2的语义相似度除由其最近公共父节点的深度决定外，也会受到该父节点处两个叶子节点所在分支的位置关系以及最小公共父节点处分支总数的影响。将最近公共父节点所含分支总数记为N，将s1与s2所在分支的间隔数记为K。在《词林》框架体系下，对s1与s2两个待计算相似度的词语，根据前面分析和相关文献中的研究结果，整合为如下相似度关键信息x：

x=D+K/N

(2)

其中，D为最近公共父节点深度；N为最近公共父节点处分支总数；K为词语所在分支间隔数。则s1与s2之间的语义相似度y可以表示为关键信息x的函数：

y=F(x)

(3)

目前所有基于《词林》的语义相似度计算模型都属于这个框架，只不过不同模型使用了不同的函数。如果把一些计算语义相似度的函数放在一起，然后再制定一个评价这些相似度计算函数的规则来评价，则这些函数就可以看成是一个具有不同竞争优势的种群。借鉴遗传算法的思想，对由相似度函数构成种群进行生物进化方面的选择、交叉和变异等操作来使种群进行不断繁衍，从而得到新的种群即新的相似度计算函数。根据自然选择优胜劣汰的规律，有理由相信能够找到比单纯通过经验建立的更好的相似度计算函数。为实现这个目标，执行以下操作：

(1)函数编码。

首先需要将函数映射为便于使用遗传算法的表示形式。该文将函数用树的形式进行编码，目的是把函数转化为利于计算机操作的形式。这种方法将函数中包含的四则运算、复合运算作为树的中间节点，将自变量x作为树的叶子节点。例如对于具有如下形式的相似度计算函数：

y=F(x)=w1x2+w2R+w3ex+w4sinx

本文的验证问题可描述为：给定系统状态转换模型TS，系统安全属性φsafe以及系统运行时的观测序列o1,…,ot，目标是 (1)计算在t时刻系统满足安全属性的概率Prt(TS φsafe|o1,…,ot;TS)，(2)当系统违背安全属性时，求解系统最大可能的执行路径作为系统违背安全属性的反例.针对该问题，图1给出了本文验证方法的框架.

(4)

其中，w1,w2,R,w3,w4为常数，则可以表示为图2所示的树状结构。

图2 函数编码的树状结构

根据这种思想，语义相似度计算函数的自变量就是上面的《词林》信息x，将基本初等函数作为基本的函数集F={x,sinx,lnx,ex,arcsinx}，取四则运算为运算集H={+,-,×,÷}。在生成函数种群时，只需从不同集合中选取元素填入相应节点，就可以生成不同的函数，反复操作2M次即可生成一个含有2M个函数的初始种群。

(2)适应度函数。

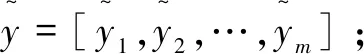
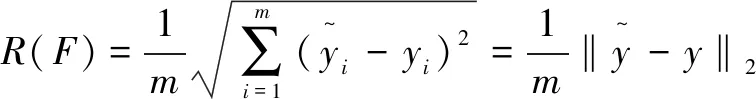
(5)

显然R(F)越小，相似度函数F的计算结果与标准结果就越接近，该个体在种群中就越优秀，具有更强的竞争力。

(3)选择。

要完成种群的更新需要从父代群体中选取部分个体，以便生存和繁衍产生下一代群体，这种操作称为选择。该文采取优者胜出的选择方法，将当前种群中的2M个函数按照适应度R(F)从小到大进行排序，然后将适应度最好的M个函数保留，将较差的M个函数淘汰，以保留下来的M个函数为基础进行下面的操作形成下一代种群。

在遗传算法中交叉是利用父代个体形成子代个体的过程，该文研究的个体是函数，在将函数编码后，随机设置交叉点，然后在交叉点处进行断开和重组，完成基因交换，生成新的个体。具体过程如图3所示，左边为选择的两个个体，图中方框处为选择作为断点的节点位置，然后分别交换和重组后，得到右侧两个新生成的个体。

图3 交叉生成新的个体

(5)变异。

遗传算法中的变异，是指将个体编码串中的某些基因用其他等位基因来替换，从而形成新个体的过程。例如图4中，左侧为选中的变异个体，其中方框处为选择的变异位置，右侧为该位置变异后生成的新个体。

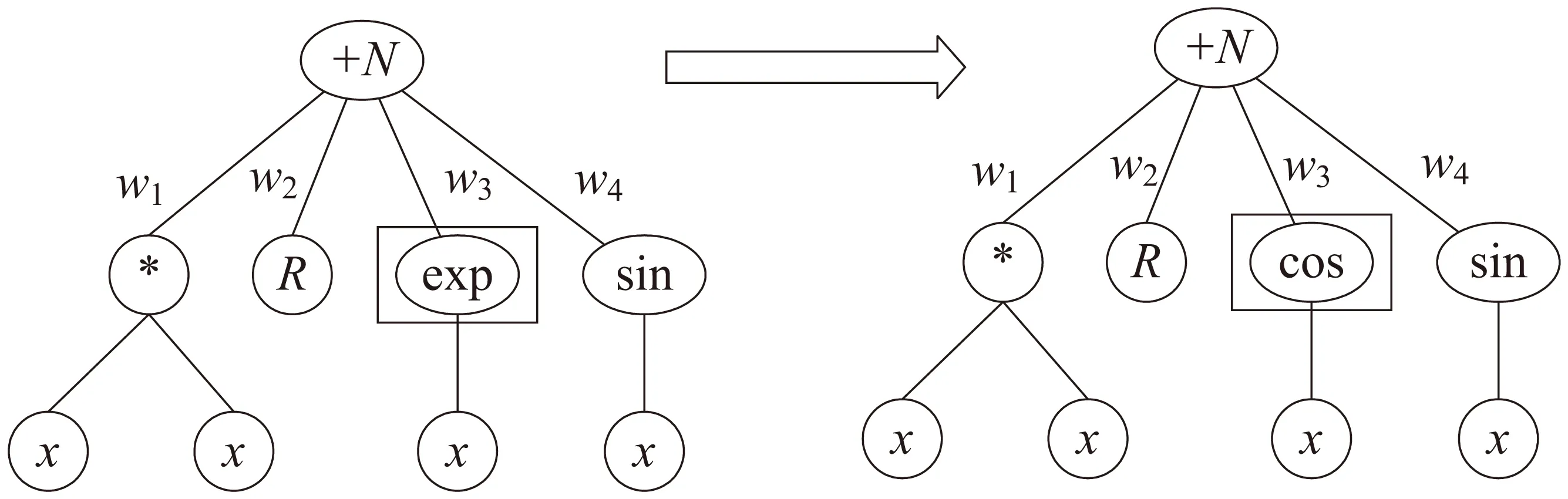
图4 变异生成新的个体

以上过程描述了一种基于遗传算法的相似度函数构建模型，该方法使用遗传算法的思想，随机生成一系列函数个体组成初始的“种群”，然后根据适应度函数来评价个体的适应度。若当前种群中的函数所计算的语义相似度都不能满足要求，则模拟生物进化中的基因变异、复制、删除等行为，繁衍生成新一代种群，经过不断迭代，寻找更好的语义相似度计算函数。下面根据遗传算法的思想为《词林》建立语义相似度计算模型，具体算法描述如下：

第1步：给定m组词语的《词林》信息{x1,x2,…,xm}和标准相似度结果{y1,y2,…,ym}，基本函数集F={x,sinx,lnx,ex,arcsinx}，运算符号集H={+,-,×,÷}，最大进化代数T。

第2步：随机生成包含2M个计算语义相似度的函数初始种群：{F1,F2,…,F2M}。

第3步：当进化代数小于最大进化代数时，生成新的计算语义相似度函数种群，完成种群繁衍迭代。具体方法如下：

①选择：计算种群内全部语义相似度函数个体{F1,F2,…,F2M}的适应度，保留M个适应度最好的语义相似度函数个体；

②交叉：随机选择两个语义相似度函数，通过交叉生成新的函数，重复四分之三M次，生成复四分之三M个新的语义相似度函数；

③变异：随机选取四分之一M个语义相似度函数，然后随机选取节点进行变异，生成四分之一M个新的语义相似度函数；

第4步：回到第3步继续进化，直到达到最大进化代数；

第5步：计算最终得到的种群中M个语义相似度函数的适应度，并将最优个体作为最终相似度计算函数。

该方法中采取了优者胜出的选择方法，每一代中的最优个体会保留到下一代中，随着种群的繁衍，该方法会得到越来越优秀的个体，即越来越好的相似度计算函数。如果达到最大繁衍代数后，得到的相似度计算函数还不够理想，可以适当增加种群大小，即增加迭代次数，甚至反复执行该方法，直到得到满意的相似度计算函数为止。

3 实验及结果分析

目前国际上对语义相似度算法的评价标准普遍采用Miller & Charles发布的30组英语词对集(简称MC30)的人工判定值作为比较或学习的标准[14-15]。该文首先根据《词林》提供的关于这30组词对的信息计算其相应的词对信息值x；然后使用遗传算法模型寻找关于x的相似度函数表达式；最后，使用新找到的模型重新计算词对相似度并与标准结果和相关结果进行对比。在试验中设定函数构成分量的长度为3；此时函数关系式可表示为：

F(x)=w1f1(x)+w2f2(x)+w3f3(x)

(6)

初始种群的数量为50，在遗传算法开始时随机产生50个函数{Fi(x),I=1,2,…,50}；此后每代种群的最大数量为100，即有100个候选函数；种群的最大进化代数为1 000代。若达到最大进化代数，则选取最后一代中最优的函数作为相似度计算模型。经过运行模型算法，最终选定的函数模型为：

(7)

利用式(7)计算得到的语义相似度结果如表3所示。

表3 语义相似度计算结果

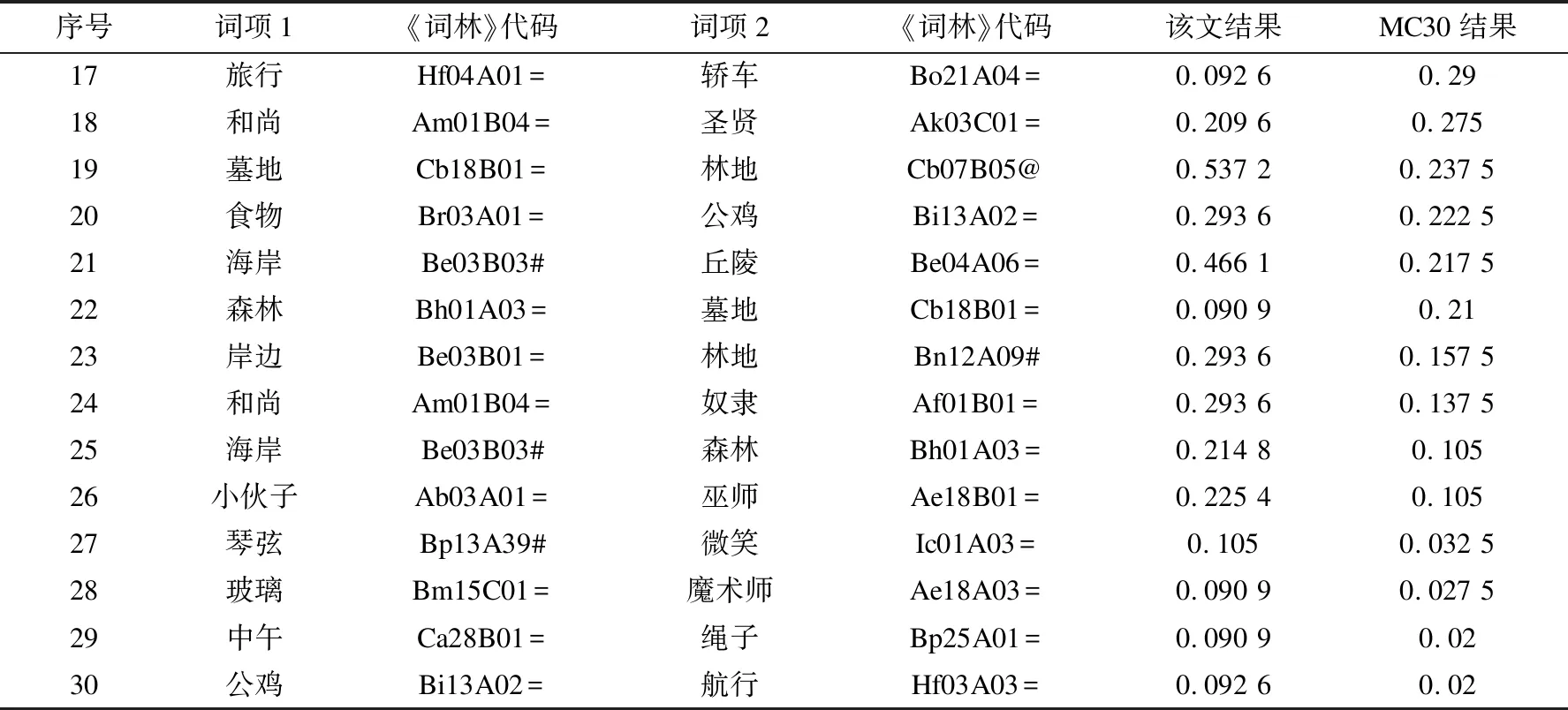
续表3

遗传算法模型对MC30语义相似度的具体计算结果如表3所示，该文计算结果与皮尔逊相关系数为r=0.864 5。在实际应用中一般认为：当r≥0.8时，两个变量间高度相关；当0.5≤r<0.8时，两个变量中度相关。以上结果说明，该文提出的语义相似度计算模型能够表达《词林》中包含的词语相似度关系，与人工值有较强的相关性。从表3中的相似度计算值中可以看出，仍然存在该文计算结果与MC30的人工判定值有较大差异的词对，比如第10个词对“食物(Br03A01=)”与“水果(Bh07A01=)”；第14个词对“兄弟(Aa02A07=)”与“和尚(Am01B04=)”。其差异的深层次主要原因是《词林》中对该词对的相似度判断标准与MC30的判断标准在语言学认识上的差异。这种差异既有不同判定者主观因素，也有不同语言之间在翻译时所带来的差异。

4 结束语

该文所提出的语义相似度计算方法是在《词林》体系中词语的深度、路径和分支节点信息基础上进行的，充分利用了人工智能遗传算法强大的搜索能力，所得相似度计算模型更为准确合理。在此研究过程中发现，已有的模型中有一些词语无论使用哪种方法，其计算结果均不理想，这种情况一般既有知识本体中义项定义或者词语分类不合理的原因，也有相似度计算模型不够完善的原因。为了克服前人研究中的不足，在知识方面充分利用《词林》已有的词语信息；在算法方面利用遗传算法从更大更广的函数空间中寻找函数模型，因此所得结论中既能得到较为理想的计算结果，也能更好地反映出语言知识层面的关系。