基于博弈和网络流的任务打包定价模型

杨焕煜，邵子朋，高汉成，沙 超，王汝传

(南京邮电大学 计算机学院、软件学院、网络空间安全学院，江苏 南京 210003)

0 引 言

“拍照赚钱”是当下新颖的一种商业模式，企业借助互联网等平台将任务发到“线上劳务市场”，“移动工作者”在平台上接受任务，完成任务并获得相应的报酬。然而，如果任务定价不合理，就会出现任务闲置的现象，而导致商品检查任务的失败。因此，如何制定一个合理的任务定价，是这种商业模式优先考虑的事情。该文提出了基于博弈和网络流的任务定价方案，在提高任务完成率的情况下使企业发布任务的成本最小。

1 基于博弈的任务定价模型

为了对“拍照赚钱”平台的任务合理定价，需要对平台已结束任务信息进行分析，从而得到平台任务的定价规律。

平台任务的定价与任务偏僻程度、周围的会员密集程度和任务密集程度有关。首先利用k-means聚类方法对任务进行聚类，并得到任务的中心点，计算任务距离中心点的距离作为任务的偏僻程度。然后利用最小二乘法拟合平台的任务定价公式M(p,c,t)，其中p为任务的偏僻程度，c为任务周围会员的密集程度，t为任务所在地任务的密集程度。

通过上述步骤可以得到平台发布任务的定价规律，但这些任务的定价并不是十分合理，如没有考虑会员信誉度因素的影响。为了弥补传统定价方案的缺陷，提高任务的完成率，对未完成的任务进行价格调整。

平台与会员之间的交易是一种不完全信息静态博弈，平台和会员都是决策者，每个决策者都有自己的决策变量和目标，决策者的行为相互影响，与之相对应的均衡概念为贝叶斯-纳什均衡[1-7]。

1.1 模型建立

假定对于每一个任务，平台的定价为Ms(vs)，即平台认为任务的价值vs时，平台给出的定价为Ms(vs)；会员的定价为Mc(vc)，即会员认为任务的价值为vc时，会员给出的定价为Mc(vc)。则vs为平台接受的最高价格，vc为会员接受的最低价格。

首先，对所建立模型做以下五条假设：

①商家知道任务对自己的真实价值vs，也就是可以支付的最高价值；会员知道任务对自己的真实价值vc，也就是自己做一单任务能接受的最低价格。

②商家不知道任务对会员的真实价值，但知道其概率分布；会员不知道任务对商家的真实价值，但也知道其概率分布。

③由k-means聚类方法得到平台发布任务的定价规律，而会员也有先验经验，对每个任务的定价有自己的估计。需要让商家的出价和会员的期望定价在相同的区间范围内浮动。这个区间只要长度范围一定，就可以任意设定，只要乘上某个参数就可以得到需要的真实值。故不妨假设vs和vc都服从[0,1]上的均匀分布。

④对一组任意给定的vs和vc，如果会员以价格m接单完成任务，则商家比预期任务定价节省m-vs，会员比预期多赚m-vc；如果不成交，双方效用都为0。平台和会员都希望自己的利润最大化，最优定价应该在vs和vc之间。

⑤以上信息为双方所共有。

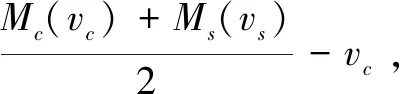
P{Ms(vs)≥Mc}

(1)

其中，E[]表示在条件Ms(vs)≥Mc下Ms(vs)的期望，P{}表示事件的概率。

P{Ms≥Mc(vc)}

(2)

如果价格组合(Mc(vc),Ms(vs))同时满足(1)、(2)，即构成一个均衡。

1.2 线性价格均衡

博弈问题存在许多均衡，该文采用线性价格均衡法。

假设会员和APP平台的报价分别是任务对二者价值的线性函数，表示为：

Mc(vc)=ac+cc·vc

(3)

Ms(vs)=as+cs·vs

(4)

确定系数ac、cc、as、cs(假设均为正数)，使二者价格组合(Mc(vc),Ms(vs))同时满足(1)、(2)。

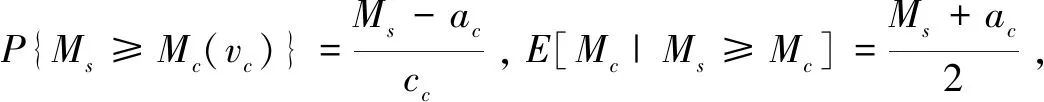
(5)

这是一个二次函数的优化，其最优解为：

(6)

类似地，假设平台的战略为(4)，则对于给定的vc，当Mc∈[as,as+cs]时，由式(1)可得会员的最优反应为：

(7)

(8)

(9)

当且仅当Ms(vs)≥Mc(vc)时交易实际上才能发生，将式(8)、式(9)代入得到交易条件为：

(10)

交易效率为能够实际发生的交易的期望价值与有利的全部交易的期望价值的比值，可求得此时任务完成的概率为[8]：

(11)

1.3 任务重新定价

寻找平台所有任务中的最高定价Mmax，设满足任务完成率为α的最小定价为Ms。由式(9)可得平台最小定价为：

(12)

联合式(10)、式(12)可得满足任务完成率为α的最小定价Ms和会员劳动力价值vc。

设任务调整的价格为f，调整未完成任务的定价，使调整后任务定价需大于Ms，即：

f=max(Mi-Ms),i=1,2,…,R

(13)

其中，R为任务总数，Mi为平台对每个任务的定价。

综上所述，任务经过调整后的定价模型为：

(14)

2 基于网络流的任务打包模型

在实际情况下，多个任务可能因为位置比较集中，导致用户会争相选择，将任务联合打包发布可以提高任务完成率，同时降低APP平台的花费。针对该问题建立网络流模型[9-14]，并建立目标函数以得到最佳任务打包方案。

2.1 网络流模型建立

构造加权有向图G={V,E}，如图1所示。网络分为四层，分别为源点S、任务点Ci(i=1,2,…,R)、会员点Di(i=1,2,…,R)、汇点T，其中R为任务总数，H为会员总数。对于图中的每一条边e∈E均带有三个权值：容量capacity(e)、流量flow(e)和费用cost(e)。在S与所有的Ci之间添加有向边，这些边的容量为1，流量为1，花费为0。

图1 网络流模型结构示意图

根据会员预定任务开始时间和信誉度确定会员优先级，预定任务时间越早且信誉度越高优先级越大，APP平台按照会员优先级从高到低给会员分配任务。首先对每个会员i，以会员为圆心寻找半径为d1圆的区域内的所有任务，然后在这些任务中不断搜寻距离最小的两个任务，若找到两个任务m、n间距离小于d2，则将这两个任务打包，并在网络中添加有向边、，且容量、capacity()=1，流量、flow()=1。由于两任务相距很近，会员完成任务方便，可以将二者的价格以一定比例降低，二者距离越近，降价越多，即：

(15)

(16)

其中，α为降价系数[15]。

剩余未打包的任务，对所有剩余任务k，若任务在已结束项目中为完成状态，则在网络中加入有向边,且容量capacity=1，流量flow=1，cost=Mk；若任务在已结束项目中未完成，则可认为此任务不会被该会员完成，此时在网络中加入有向边,且容量capacity()=1，流量flow()=0，cost()=0。

最后在所有Di与T之间添加有向边，对于会员i，容量为该会员的预定任务限额，即：

capacity()=li

(17)

流量为该会员完成的任务总数，即：

(18)

花费为该会员完成任务的花费总和，即：

(19)

至此，网络流模型建立完成。

2.2 目标函数确定

以平台花费最少、任务完成数量最高为目标求解出的打包的方案即为所求的任务打包方案，即目标函数为：

(20)

3 模型求解

该文使用的数据集来源于2017年高教社杯全国大学生数学建模竞赛。对任务数据信息进行分析得到平台任务定价规律，并根据以上建立的基于博弈的任务定价模型和基于网络流的任务打包模型对任务定价方案进行变更，求解出最佳任务定价、打包方案。

3.1 求解平台定价规律

首先将所有任务信息、会员信息导入地图，并在地图中标注所有任务信息。导入后发现大部分任务是分布在广东省内的佛山、广州、东莞、深圳四个城市之中，有若干任务点分布偏离太大作为异常数据不予处理。

会员分布如图2所示，导入后发现大部分会员是分布在广东省内的佛山、广州、东莞、深圳四个城市之中，有若干会员分布偏离太大作为异常数据不予处理。

图2 会员分布

对任务坐标点进行聚类分析，根据任务的密集程度可将任务分为四类，四类任务的中心点分别位于广州、东莞、深圳、佛山四个城市，即每类任务都以其中心城市为中心向周围扩散。用k-means聚类算法画出任务分布的聚类图，如图3所示。

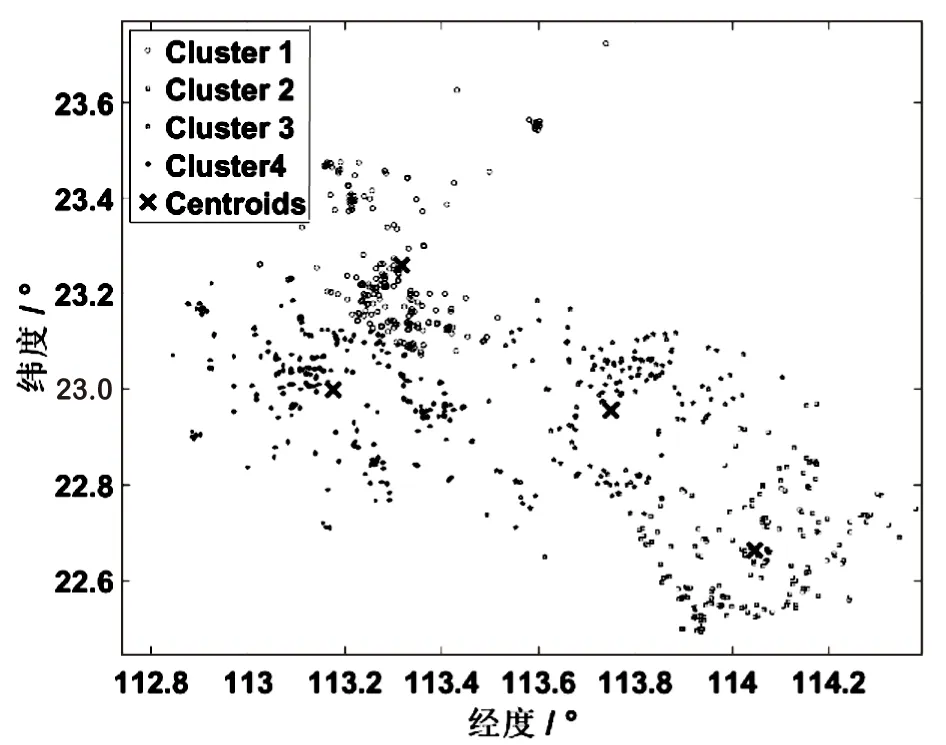
图3 任务聚类

计算任务距离中心点的距离作为任务的偏僻程度p，任务的偏僻程度越大，任务定价越高。以每个任务为中心，半径2 km的范围内会员的数量记为会员的密集程度c，半径2 km的范围内任务的数量记为任务的密集程度t，会员、任务密集程度越大，任务定价越低。

利用最小二乘法拟合平台的任务定价公式M(p,c,t)，分别尝试拟合一次、二次、三次函数，发现拟合出的二次和三次函数误差相差不大，因此这里采用二次函数形式，得出平台的任务定价规律如下：

M=72.203+0.062 7·c2-0.797 7·c+

0.018 9·t2-0.702·t-0.000 091 476·p2+

0.021 6·p

(21)

分析可知当前任务未完成原因主要有：

①任务完成率与任务定价水平有关，标价越高的任务，完成率越高。

②繁华地带任务未完成率远大于外围地区。这可能是因为市中心人们生活节奏快、工资高、空闲时间少，任务定价没有足够的吸引力等。而外围地区恰好相反。

③与地区收入水平有关，比如深圳会员数量多、交通好，但定价相对太低，对人群没有足够的吸引力。

④地理位置：地理位置的差异会影响到任务的完成。当地形复杂时，任务也就变得更加困难，导致任务的无法完成。

⑤人口密度：在人口密度小的地方，会有很多任务未完成。

⑥突发状况：实际生活中，人们总会遇到各种事情，心情不好、堵车、假期、店家拒访等。这些突发状况使任务完成的可能性降低。且天气恶劣时，人们的参与意愿会降低，可能会由很多任务未完成。

3.2 基于博弈的任务定价模型求解

计算佛山、广州、东莞、深圳四个区域已结束任务的完成率分别为67.4%、54.7%、95.3%、36.2%。由于东莞任务完成率以达到95.3%这一较高水准，因此不再对以东莞为中心的区域内的任务进行定价调整。利用上述任务定价模型分别对佛山、广州、深圳三个区域内的任务进行重新定价。求解出佛山、广州、深圳三个区域的会员劳动力价值、最小定价、价格调整大小，如表1所示。

表1 会员劳动力价值、最小定价和价格调整大小

新定价方案与原定价方案进行比较，原定价方案中平台需支付总花费为57 707.5，调整定价后平台总支付花费为60 011.5，平台每件任务平均花费上涨3.9%，任务完成率整体提高到95%，即总任务完成率提高了31.6%。

与应用基于博弈论的任务定价模型之前的任务完成情况对比可知，平台增加的花费相比于任务完成率的上涨程度可以说微不足道，平台在微小的损失下大幅度提高了任务完成率，体现了任务定价模型的普适性与最优性。可以说，通过价格博弈模型的定价方案，最大化了APP平台和会员的利润。

3.3 基于网络流的任务打包模型求解

基于任务、会员地理位置信息，设置合适的搜索半径；根据市场规律，设置降价系数α=0.5。对上述网络流模型进行求解，求解出共有152个任务被打包为76组任务包，部分打包结果如表2所示。

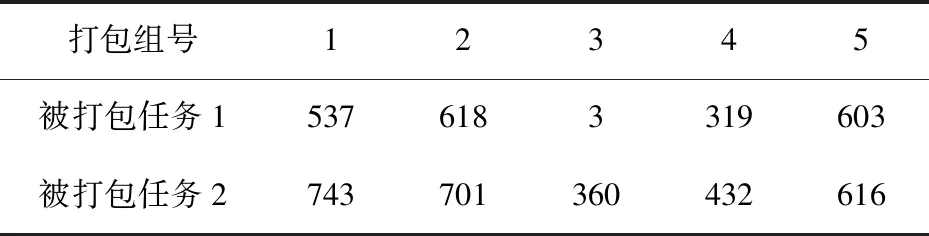
表2 部分打包结果

计算打包后平台所需支付总花费为57 416元，相比于第一步修改定价后平台总花费下降了2 595元。同时总任务完成率为95.45%。

通过基于网络流的任务打包模型，在降低平台花费的同时任务完成率仍略有提高，进一步提高了APP平台和会员的利润，充分证明了模型的有效性和正确性。

4 灵敏度分析

针对任务打包模型，为了进一步检验采用的搜索半径、降价系数的合理性，该文对搜索半径和降价系数分别进行了灵敏度分析。

4.1 搜索半径灵敏度分析

根据任务和会员的密集程度，该文以0.1为步长，在搜索半径范围内计算任务打包结果、任务完成率及平台的总花费数额，计算结果如表3所示。

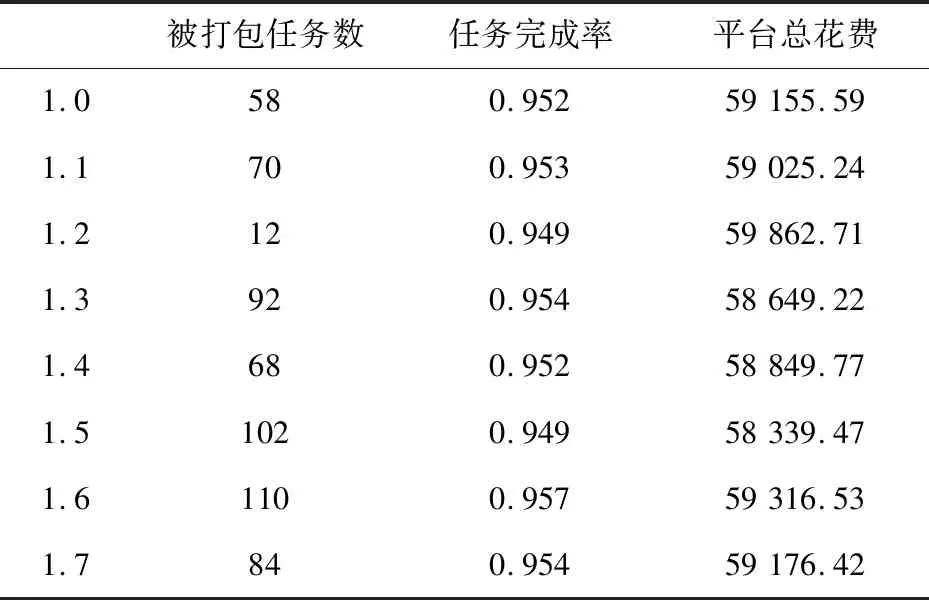
表3 搜索半径灵敏度分析

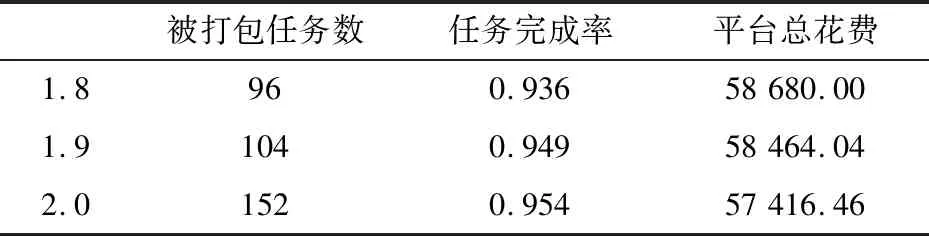
续表3

为了更加清楚地显示搜索半径对任务打包结果的影响，根据以上结果作散点图，如图4、图5所示。

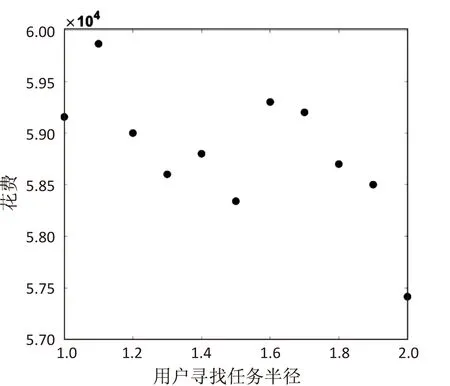
图4 搜索半径对平台花费的影响

图5 搜索半径对任务完成率的影响

由图4、图5可知，在范围内任务的完成率和平台的花费金额均呈波动状态。在文中取值时，APP平台的花费最低且任务完成率相对较高，此时APP平台和会员双方得到的利益最大。

4.2 降价系数灵敏度分析

为了增加可信度与真实性，该文对降价系数进行灵敏度分析。以0.1为步长，在范围内计算平台的总花费数额，绘制降价系数对APP平台花费的结果，如图6所示。

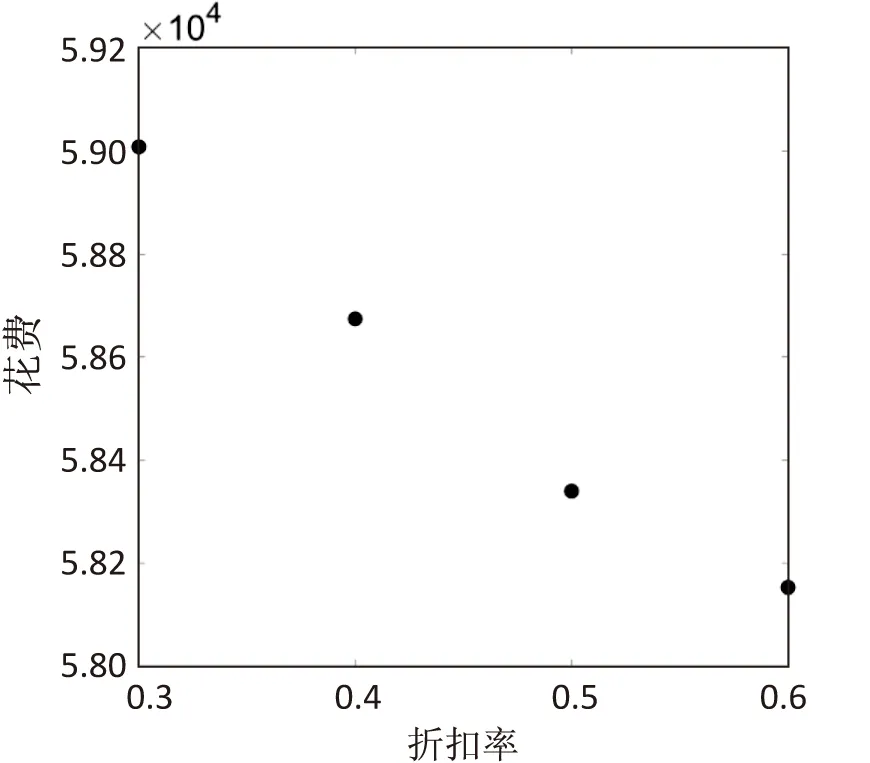
图6 降价系数对平台花费的影响

由图6可知，APP平台的花费会随着降价系数的增加而减少。但是根据任务未完成原因的分析，任务完成率与任务定价水平有着密切的关系，在实际生活中标价越高的任务，完成率越高，当标价过低时任务对用户的吸引力也会有所降低，因此采取较为折中的降价系数α=0.5。

5 优势与创新点

该文提出的定价规律模型的建立更多基于理性分析和合理推导，结合实际情况对任务完成情况给出解释。利用多元回归方程刻画任务定价的各项细节，将任务定价问题一般化，从而避免了当数据发生变动时，定价原则随之变动的问题。

考虑到商家与会员之间的价格博弈的关系，切合实际，利用博弈论很好地模拟出任务的完成率，并且保证了商家收益尽可能大。

建立任务打包模型，从网络流中最小费用最大流的视角看待整个问题，在最大化任务完成率的同时将公司所需费用考虑在内。打包原则贴合实际容易被人们接受。

在数据处理方面，针对所给数据进行详细分析，得到任务执行的具体情况，在进一步进行划分后，得到的数据具有比较明显的地域特征，为制定定价方案提供了数据资料。

6 结束语

提出了基于博弈和网络流的任务打包定价模型，即在已结束的任务信息基础上，首先引入贝叶斯-纳什均衡理论重新建立任务定价方案，然后再基于最小费用最大流思想建立网络流模型将部分任务联合打包发布，在保障任务的完成率的前提下使企业付出酬金最小。在所用示例中，重新定价后，平台任务完成率提高至95.45%。

但是在引用博弈论时将每个城市的所有会员的理想价格定为统一的价格，没有考虑各个会员之间的经济、社会地位等因素会对理想价格的影响，从而使理想价格与个别会员存在一定偏差。

“拍照赚钱”这种移动互联网下的一种自助式服务模式正随着移动互联的发展不断在人们的日常生活中普及。该文基于移动互联网下“拍照赚钱”的任务定价与打包模型有着重要的现实意义，对于任务接受者来说，完成多个任务所需的时间更少，获得的报酬更高，获取适合自己的任务信息更加方便。对于“拍照赚钱”软件来说，增加了任务完成率，能够吸引更多人使用该任务平台，增加了软件平台的收入。该文采用多元非线性回归方法以及基于网络流的最小费用最大流算法所建立的任务定价与打包模型在日常生活中的诸多问题中也有着广泛应用，对其他定价、规划问题也有一定的指导作用。