融合残差网络和极限梯度提升的音频隐写检测模型

陈 朗，王让定，严迪群，林昱臻

（宁波大学信息科学与工程学院，浙江宁波 315211）

（*通信作者电子邮箱wangrangding@nbu.edu.cn）

0 引言

伴随着互联网和多媒体处理技术的飞速发展，互联网平台上涌现出越来越多的数字媒体应用，数字媒体安全问题变得日益突出，已成为数字经济等领域迫切需要解决的难题。在信息安全领域，保障信息安全的技术有密码术和信息隐藏。然而，应用密码术获得的密文在公开信道上传输，很容易引起第三方的监听进而采取手段破坏隐蔽通信；信息隐藏则很好地解决了密码术存在的问题，它将密信以“暗度陈仓”的方式隐藏在另一非机密载体中进行传输，从而可实现隐蔽通信。广义的信息隐藏包括隐写术和隐写分析：隐写术利用人类感官对数字信号的感知冗余性将秘密信息隐藏到数字媒体中，目的是避免引起检查者的注意；相反的，隐写分析则是通过分析载体对象和嵌密对象在感知和统计特征上的差异来判别载体中是否隐藏密信。

近二十多年来，研究人员在采用传统方法进行音频隐写分析方面做了大量工作，主要集中于手工特征的设计上。Johnson 等［1］通过短时傅里叶变换（Short-Time Fourier Transform，STFT）提取音频统计特征，以支持向量机（Support Vector Machine，SVM）作为分类器；实验结果显示，该方法对较低嵌入率下最低有效位（Least Significant Bit，LSB）隐写算法并不能有效检测。Kraetzer 等［2］第一次提出了基于梅尔倒谱（Mel-cepstrum）的网络协议（Internet Protocol，IP）语音隐写检测方法，以梅尔倒谱特征作为SVM 的输入。Liu等［3］提出了基于时域导数频谱和梅尔倒谱的音频隐写检测方法，以傅里叶频谱统计和二阶差分滤波器获取的梅尔倒谱系数作为提取的手工特征，采用SVM 作为分类器；实验结果显示，相较于仅提取梅尔倒谱特征的方法，该方法的检测准确率有明显提高。Liu 等［4］将梅尔倒谱系数和根据二阶差分滤波器获取的马尔可夫转移矩阵作为提取的手工特征，并研究了音频信号复杂度和检测准确率之间的关系；实验结果表明，对LSB等低隐蔽性隐写算法检测准确率达到90%以上。Geetha 等［5］设计了一种基于音频质量测度的特征，计算载体音频和嵌密音频的Hausdorff 距离作为失真度测量特征。王昱洁等［6］提出了一种基于改进离散余弦变换（Modified Discrete Cosine Transform，MDCT）量化系数统计特征的高级音频编码（Advanced Audio Coding，AAC）隐写检测方法，从MDCT 量化系数中提取了广义高斯分布模型的参数、量化系数分布直方图的频域统计矩、帧内和帧间MDCT 系数的隐马尔可夫转移矩阵的部分数据作为手工设计的特征，采用SVM 作为分类器；实验结果表明，该方法对基于MDCT 量化系数的直接扩频隐写算法检测效果较好。王昱洁等［7］还提出了一种基于模糊C 均值聚类（Fuzzy Cmeans Clustering，FCC）和单类支持向量机（One Class Support Vector Machine，OC-SVM）的音频隐写检测方法，首先提取短时傅里叶频谱统计特征和基于音频质量测度的特征，然后对提取的特征进行FCC聚类从而得到C个聚类，最后以OC-SVM作为分类器；实验结果表明，对几种经典隐写算法在满嵌时总体检测率达到85.1%。Han 等［8］提出了一种基于线性预测的音频隐写检测方法，提取了线性预测系数、线性预测残差、线性预测频谱和线性预测频谱系数，将它们的最大值作为SVM的输入特征；实验结果表明，该方法对四种低隐蔽性传统隐写算法的检测准确率均在96%以上。Ren 等［9］提出了一种基于帧内和帧间的改进离散余弦变换系数差异的高级音频编码音频隐写检测方法。

随着人工智能时代的到来，不同的深度学习网络相继被提出，在许多领域已经达到了目前最好的效果，尤其是在语音识别和计算机视觉领域。Chen 等［10］首次提出了针对LSB 匹配隐写的卷积神经网络（Convolutional Neural Network，CNN），该方法的检测准确率高于手工提取特征的传统方法。随后，Lin等［11］提出了一种改进的CNN，首先采用四阶差分滤波器计算残差进行预处理，其中滤波器参数在网络中设置为可训练的；再将预处理后的音频数据输入到网络中，采用迁移学习的策略进行低嵌入率下音频隐写检测。Wang 等［12］提出了一种在熵编码域（Entropy Code Domain）对MP3 进行隐写分析的CNN，使用量化改进的离散余弦变换（Quantified Modified Discrete Cosine Transform，QMDCT）特征作为网络的输入的浅层特征，准确率相较于以前的隐写分析方法提升了20%以上。Yang 等［13］融合了CNN 和循环神经网络（Recurrent Neural Network，RNN）的优势，提出了一种联合CNN 和长短期记忆（Long Short-Term Memory，LSTM）网络的模型CNN-LSTM 用于检测网络协议语音流（Voice over Internet Protocol，VoIP）上基于量化索引调制（Quantization Index Modulation，QIM）的隐写算法，其中的LSTM 用于学习音频载体的上下文信息，CNN用于学习分类特征。

然而，上述方法不能有效检测高隐蔽性音频信息隐藏算法，如STC框架［14］下的音频隐写算法。基于此，本文提出了一种融合深度残差网络和极限梯度提升（eXtreme Gradient Boosting，XGBoost）［15］的音频隐写检测模型ResNet-XGBoost。基于ResNet-XGBoost模型的音频隐写检测方法首先采用残差网络模型提取输入音频的高维抽象特征，再用XGBoost 模型对残差网络提取的高维抽象特征进行分类。实验结果显示，该方法对STC音频隐写算法在三种不同嵌入率下的检测准确率相较于传统提取手工特征的检测方法和基于深度学习的检测方法均有显著提升。

1 STC框架

STC 框架下的隐写算法属于一种基于校验网格编码的最小化嵌入失真隐写算法，具备嵌入容量大、安全性高等优势。隐写设计者先定义失真函数，采用维特比算法获取合适的原始载体修改模式，使得嵌入秘密信息后的总体失真接近理论最小值；而接收方不必知道失真函数，仅根据校验矩阵便可提取出密信。

假设原始载体为二进制向量X∈{0，1}n，嵌密载体Y∈{0，1}n，秘密信息M∈{0，1}m，且n≥m。定义嵌入函数为Emb：{0，1}n×{0，1}m→{0，1}m，提取函数为Ext：{0，1}n→{0，1}m且满足如下条件：

构造一个矩阵（亦即校验矩阵，其结构如图1 所示），使得嵌密载体满足：

若嵌入操作相互独立即互相不影响，则嵌入密信后引起的载体失真为加性失真。定义嵌入密信后的总失真函数为：

其中：D(X，Y)为嵌入密信后的总失真；i为当前载体位置索引；n为载体长度；ρi为当前元素变化引起的失真，在复杂区域取值较小，在平滑区域取值较大。

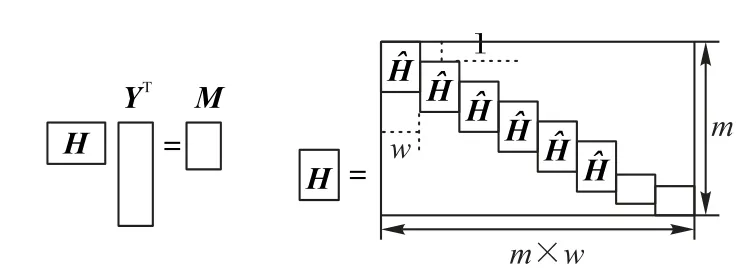
图1 校验矩阵示意图Fig.1 Schematic diagram of check matrix

STC 隐写的目标是使得总失真函数尽可能小，即求解最优的Y，既满足HYT=M又使D(X，Y)最小，其嵌密和提取过程的数学表达为：

STC 过程在网格图上完成，求解Y时可将所有满足条件HYT=M的可行解Y在网格图中用一条路径表示。STC 在所有路径中选择具有最小权重的路径，该路径对应一个最佳矢量Y，使HYT=M，并且使得嵌入总失真函数D(X，Y)达到最小。维特比算法包括前向计算和反向计算，利用该算法可求解出最佳Y。

STC 音频隐写一般将STC 和失真代价结合。首先利用失真函数计算载体中每个元素被修改后的失真代价，再应用STC 确定需要修改的位置并进行嵌密操作，从而得到嵌密音频。STC音频隐写流程如图2所示。

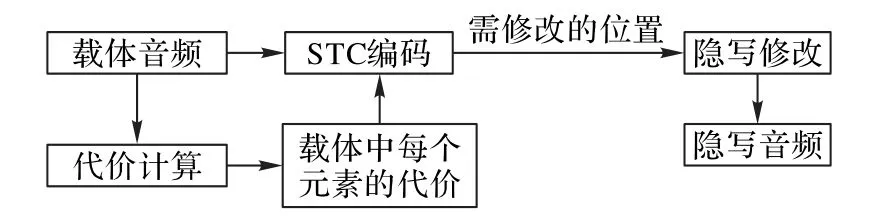
图2 STC音频隐写流程Fig.2 Flowchart of audio steganography based on STC

2 极限梯度提升算法

XGBoost 是［15］一种改进的梯度提升算法，改进点在于采用二阶导数优化目标函数。它融合多个弱分类器进而演化成强分类器，基分类器为分类回归树（Classification And Regression Tree，CART）。

XGBoost 的目标函数由训练损失和正则化项两部分组成，定义如下：

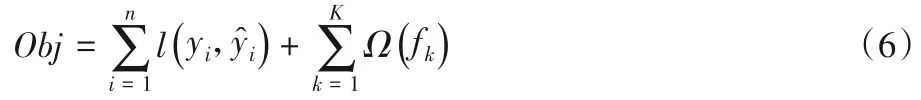
其中：fk为第k棵树模型的函数表达式；yi为第i个样本xi的真实标签为第i个样本xi的预测值。而XGBoost 是一个加法模型，故预测值为每棵树预测值的累加之和，即

将K棵树的复杂度之和作为正则化项，用于防止模型过拟合。假设第t次迭代训练的树模型为ft，则有：

XGBoost 模型在训练过程中，当建立第t棵树时，采用贪心策略进行树节点的分裂。每次分裂成左右两个叶子节点后，会给损失函数带来增益，其定义如下：

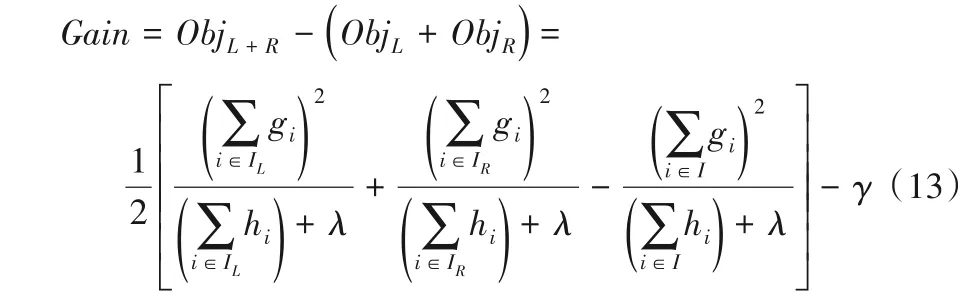
若Gain＞0，则将此次分裂结果加入模型构建中。

3 基于模型融合的音频隐写检测

3.1 ResNet-XGBoost模型总体结构

考虑到卷积神经网络在特征提取上的优势，本文提出了一种基于ResNet-XGBoost模型的音频隐写检测方法。该方法的思路是利用残差网络提取高维抽象特征，并将其作为XGBoost 分类器的输入，再结合实验结果和网络结构调整得到最终的模型结构，如图3 所示。首先，输入到模型中的音频通过高通滤波器（High-Pass Filter，HPF）的预处理后，利用第一阶段的三个卷积层进行初步特征提取；接下来，经过五个阶段的残差块和池化操作进一步提取深层次特征；最后，经过全连接层和Dropout［16］层将最终提取的特征作为XGBoost 分类器的输入进行分类，进而输出模型分类结果。

3.2 截断线性单元

在神经网络中应用非线性激活函数可增强特征学习能力。到目前为止，Sigmoid、Tanh、修正线性单元（Rectified Linear Unit，ReLU）等非线性激活函数已相继提出，其中尤以ReLU 在计算机视觉等领域应用较好的泛化能力。ReLU 表达式如下：

ReLU 能适应计算机视觉领域被检测目标的数据分布（被检测信号信噪比较高），但在隐写分析任务中由于隐写噪声微弱即被检测信号信噪比低，若采用ReLU 激活函数，会使得模型不能提取有效的特征。因此，引入了如下的线性截断单元（Truncated Linear Unit，TLU）［17］激活函数：

其中，超参数T为线性截断阈值，根据实验确定。

本文方法在阶段1 的第一个卷积层的卷积核大小为1× 1，卷积核个数为8，且使用了TLU 激活函数，实验中发现T=3 时，检测效果较好；第二个卷积层的卷积核大小为1× 5，卷积核个数为8；第三个卷积层的卷积核大小为1× 1，卷积核个数为16。

图3 本文模型总体结构Fig.3 Overall structure of the proposed model

3.3 池化层

为消除特征中的冗余信息和减少来自卷积层的参数个数，通常在卷积层后进行池化操作。池化也可被认为是一种卷积操作，分为最大池化和平均池化。最大池化输出滑动窗口的最大值，用于提取纹理特征；平均池化输出滑动窗口的平均值，用于保留背景信息。根据隐写分析任务的特点和实验效果，本文使用了平均池化，可在一定程度上防止过拟合，为使模型更好地学习到残差，需在第6 阶段后汇聚高维特征，因此，除了第6 阶段残差块后使用了全局平均池化，其余阶段均使用平均池化，池化窗口大小为1×3，步长为2。

3.4 残差层

残差网络最早由He等［18］提出并应用于图像识别，设计了一个多达152 层的深度卷积神经网络，在ImageNet 大规模视觉识别挑战赛图像分类任务上识别错误率仅为3.57%，夺得了图像分类组第一名。残差网络在CNN 的基础上做出了些许改进，有效避免了梯度消失和梯度爆炸的问题，解决了CNN层数过深时准确率下降的缺陷，残差块基本结构如图4 所示。假设某段神经网络的输入为x，期望输出为H(x)，则在残差块中学习目标为F(x)=H(x)-x，其中F(x)为残差。

图4 残差块基本结构Fig.4 Basic structure of residual block

将输入音频x记为：

其中：c为载体音频；0代表零信号，即无隐写；m为嵌入秘密信息后产生的微弱信号。

将x输入到残差学习块中，恒等映射块将x传输到输出节点，同时，残差学习块F(x)将学习到残差m，并将其与输入x汇合输出。因此，可将残差m类比为隐写噪声，利用残差学习即可学习到隐写噪声的数据分布，使得残差网络非常适合于隐写分析任务。

本文残差网络模型采用的残差块如图4 所示。残差映射部分由3 组基本单元构成，其中基本单元包括1× 1 卷积核、1× 5 卷积核、批规范化和tanh 激活函数。在该残差块中，输入维度为D，经过残差学习后，输出维度为2D。在本文残差网络模型中，阶段2～阶段6中“5个残差块堆叠”后面括号内的参数分别表示输入和输出维度。以阶段2 为例，（16，32）表示残差块的输入维度为16，输出维度为32。每个阶段的残差层由5个结构如图5所示的残差块堆叠而成，其输入维度和输出维度按图3中残差层参数设置。

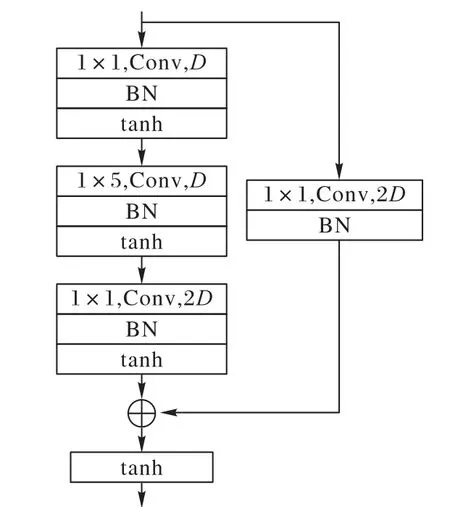
图5 本文采用的残差块Fig.5 Residual block used in the paper

3.5 全连接层和Dropout层

本文模型ResNet-XGBoost 的残差网络中有两个全连接层，并且分别在每个全连接层后加入了一个Dropout［16］层，其中第一个全连接层的神经元个数为1 024，第二个全连接层的神经元个数为256。

在训练深度神经网络时难免出现过拟合现象，为解决这一问题，通常的思路是采用模型集成，即训练多个模型进行组合，但是训练多个模型会耗费巨大的计算量。因此，Dropout作为一种典型的正则化手段应运而生，一定程度上能有效防止出现过拟合。通俗地讲，Dropout 就是在神经网络前向传播过程中，以一定概率p∈{0，1}抑制神经元，在测试时，激活所有神经元，但需将每个神经元的输出乘以p。

假设一个神经网络有L个隐藏层，l∈{1，2，…，L}为隐藏层数序号，z(l)为第l层的输入向量，y(l)为第l层的输出向量，w(l)和b(l)分别为第l权重和偏置。则若在前向传播过程中不使用Dropout，对隐藏节点i有：

其中：l∈{0，1，…，L-1}，f为激活函数。

若在前向传播过程中使用Dropout，对隐藏节点i有：

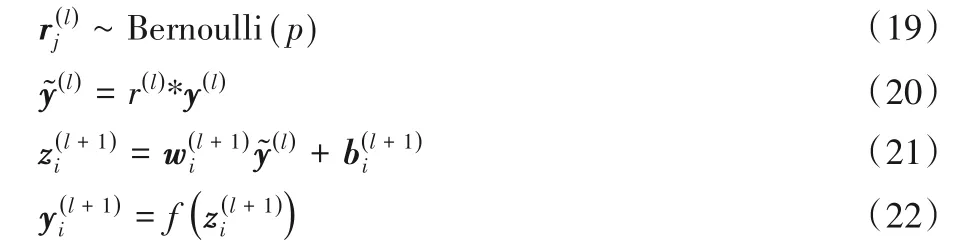
其中：Bernoulli函数的作用是以概率p随机生成一个由0、1 组成的向量；y(l)为第l层隐藏层的输出。

实验中通过多次调参发现，第一个Dropout层抑制概率取0.3，第二个Dropout 层抑制概率取0.1 时，提取的特征输入到XGBoost分类器中的检测效果最好。

3.6 XGBoost分类器

本文方法的思路是先利用残差网络提取高维抽象特征，再将提取到的输入到XGBoost 分类器中进行分类。XGBoost分类器融合多个分类回归树进行分类，具有较好的泛化能力，其参数设置显得尤为重要。实验中多次调参得出XGBoost 分类器最优参数组合：学习率取0.1，树的深度取150，训练轮数取1 000，其余均为默认的参数，此时检测性能可达到最优。在XGBoost 模型训练过程中，使用了logistic 和hinge 两种损失函数，其表达式分别为：

其中，z1、z2均为分类器的预测输出。

对于XGBoost 分类器来讲，使用logistic 损失函数时，分类器输出给定输入样本属于正类的概率；使用hinge 损失函数时，分类器输出给定输入样本的分类结果。在实验中发现，在保持除了损失函数外的所有参数不变的条件下，损失函数为hinge时的分类准确率明显高于logistic。

4 实验与结果分析

4.1 实验设置

实验数据集来源于TIMIT 语料库［19］，其中包含6 300 个采样频率为16 kHz、量化位数为16 的无压缩单声道音频，将每段语音切割成时长为1 s的音频片段，选取其中15 000个作为用于隐写的原始音频，并分别利用LSBM 和STC 隐写算法嵌入密信，从而生成15 000个嵌密音频。

实验时将15 000个原始音频和15 000个嵌密音频组合在一起，合计30 000个音频片段，其中，24 000个为训练集，6 000个用于验证与测试。残差网络模型的训练批次大小为64，输入到XGBoost 分类器中的高维抽象特征维度是256。实验硬件环境是内存大小为11 GB 的NVDIA GTX1 080Ti GPU，软件环境是Tensorflow和Keras深度学习框架。

4.2 模型微调对实验结果的影响

4.2.1 高通滤波器阶数对检测准确率的影响

本文采用的高通滤波器为差分滤波器［4］，在训练过程中发现，将其参数设为固定时检测效果较好。隐写相当于向原始载体中添加了微弱的噪声，需比较嵌入密信前后的载体差异即计算残差，以此提高信噪比，使得特征学习更充分。为研究滤波器阶数对检测准确率的影响，分别在嵌入率为0.5 bps（bit per sample）时对LSBM 和STC 进行检测，实验结果如图6所示。实验结果表明，高通滤波器阶数取6 时，隐写检测准确率最高；当滤波器阶数大于6时，隐写检测准确率反而下降。

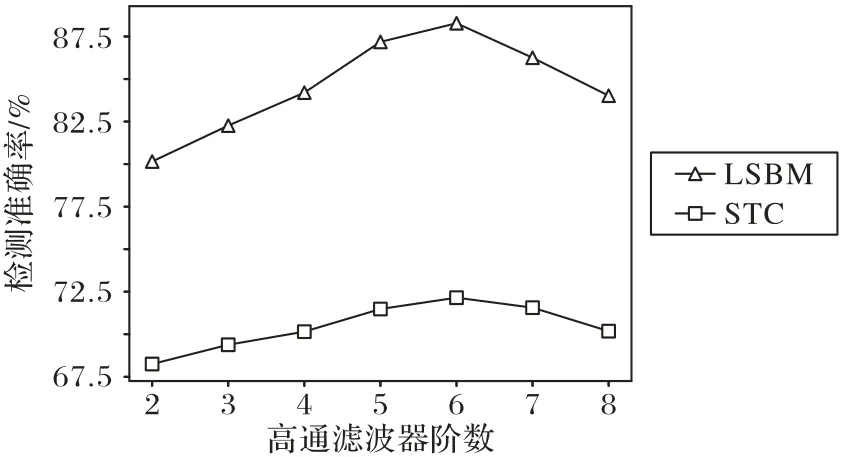
图6 高通滤波器不同阶数对应的检测准确率Fig.6 Detection accuracies corresponding to different orders of HPF

6阶高通滤波器参数设置如下：

4.2.2 模型结构对检测准确率的影响

通过修改用于提取特征的残差网络的不同结构参数，比较每种修改情况下对LSBM 隐写算法的检测准确率，其中LSBM 嵌入率为0.5 bps，修改的网络结构参数如表1 所示。为比较修改不同的网络结构参数后模型检测准确率的波动范围，对于每个不同的模型进行10次实验，实验结果如图7的箱形图所示。本文模型平均检测准确率为86.58%，与其他9 种模型相比，检测准确率最高且较稳定；模型#2 的平均检测准确率为83.48%，原因可能是移除高通滤波器后，模型不能有效学习到残差；模型#3 的平均检测准确率为82.59%，原因可能是移除TLU激活函数后，模型提取的特征数据缺失规范化；模型#4 和#5 的检测准确率介于81.12%和86.85%之间且波动范围较大；模型#6 的检测准确率在75.12%和87.25%之间，有时检测准确率高于模型#1，但有时检测准确率陷入局部最小值；模型#7 的检测准确率波动范围小，但平均检测准确率仅为79.14%，原因是梯度消失；模型#8 的检测平均检测准确率为85.6%，原因是可能发生过拟合；模型#9 的平均检测准确率为74.72%，在9 种模型中是最低的，恰恰印证了XGBoost 分类器的有效性。XGBoost 分类器能提高检测准确率的一个重要原因是，XGBoost 模型在训练过程中不断优化当前决策树，并融合多棵当前最优决策树进行分类，是集成学习的一种体现。综上所述，本文模型收敛快，检测准确率最高，因此，相较于其他8种模型，本文模型是最有效的。

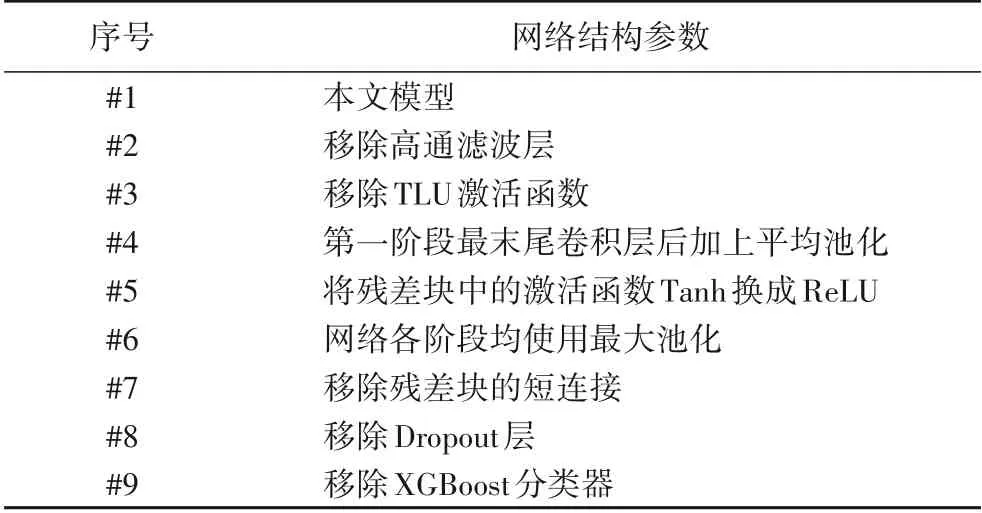
表1 修改的网络结构参数Tab.1 Modified network structure parameters

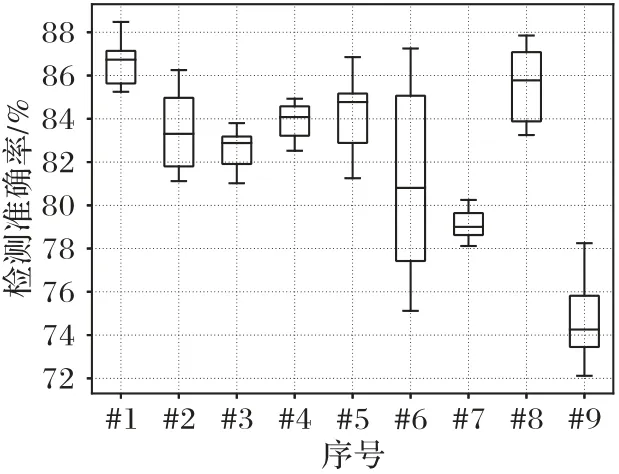
图7 嵌入率为0.5 bps时不同模型的LSBM隐写检测准确率箱形图Fig.7 Box plots of the detection accuracies acquired from different models for LSBM steganography with embedding rate of 0.5 bps

4.3 结果对比分析

为进一步证实本文方法的优势所在，对比了文献［3-4，20］分别提出的传统基于手工特征的音频隐写检测方法和文献［11］提出的深度学习检测方法对LSBM 和STC 在不同嵌入率下的平均检测准确率，其中平均检测准确率为10 次重复实验结果取平均值。对于STC 嵌密，为研究嵌入率相同即子校验矩阵宽度相同而子校验矩阵高度不同对隐写检测准确率的影响，由于在STC 隐写中，子校验矩阵高度取值范围为6 ≤h≤15，为简化实验，分别在子校验矩阵高度为7、8和9 时进行嵌密。实验结果如表2、3所示。

从表2可知，本文方法对三种不同嵌入率下的LSBM 隐写算法检测准确率相较于文献［3-4，20］和文献［11］的方法均有明显提升。对0.5 bps 的LSBM 隐写检测，本文方法的准确率比文献［3-4，20］和文献［11］的方法分别提高了28.46 个百分点、16.23个百分点、15.22个百分点和10.16个百分点。

表2 不同检测方法对LSBM隐写检测准确率 单位：%Tab.2 Detection accuracies of different detection methods for LSBM steganography unit：%

表3 显示了不同方法对子校验矩阵高度分别为7、8 和9时的STC 隐写算法检测准确率，可知本文方法对不同嵌入率下的STC 隐写算法检测准确率明显高于文献［3-4，20］和文献［11］的方法，且已达到了目前最好的效果。以STC 隐写子校验矩阵高度h=7 时为例，本文方法对0.5 bps 的STC 隐写算法检测准确率比文献［3-4，20］和文献［11］的方法分别提高了22 个百分点以上、12.75 个百分点、12.25 个百分点、11.07 个百分点。文献［3］方法不能检测STC 隐写算法的一个重要原因是，STC 隐写会使得嵌入密信后引起的失真最小，即隐写噪声极其微弱，以此保证STC隐写具有很高的隐蔽性，使得基于传统手工特征的音频隐写检测方法很难提取到有效的特征。通过表3 的实验结果可知，就STC 隐写而言，子校验矩阵高度越高，安全性越高，即越抗隐写检测。

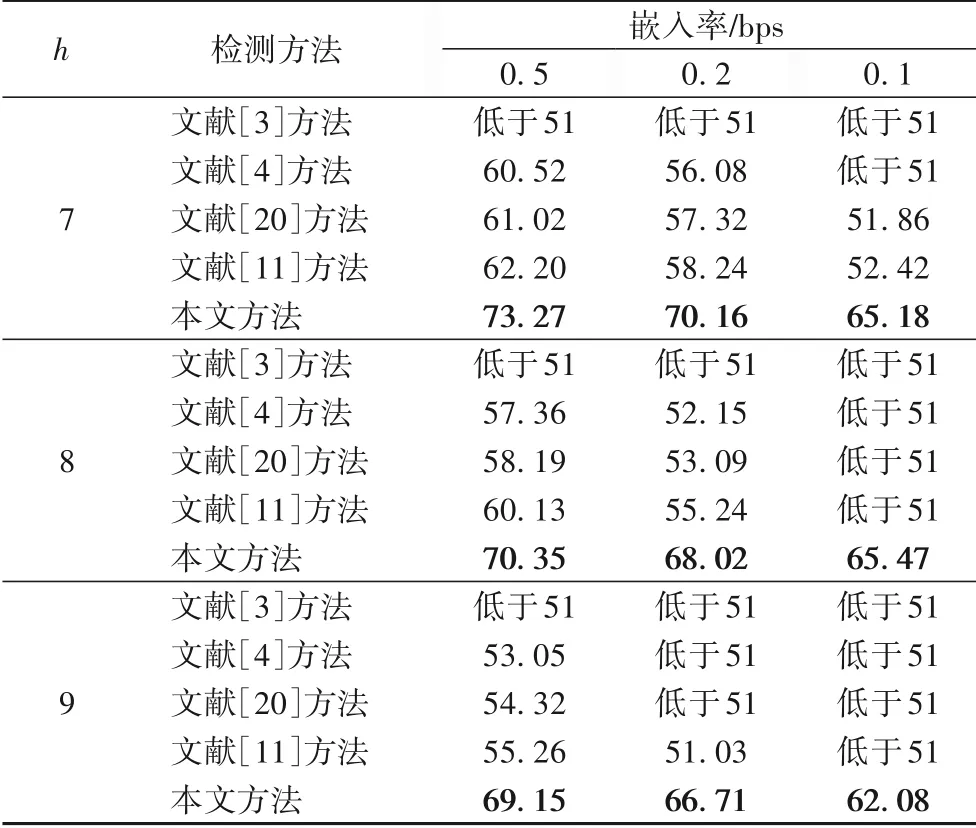
表3 不同检测方法对h=7，8，9时的STC隐写检测准确率单位：%Tab.3 Detection accuracies of different detection methods for STC steganography when h=7，8，9 unit：%

同时，对于0.5 bps的LSBM隐写和STC隐写（子校验矩阵高度h=7）检测，文献［11］方法和本文方法的ROC 曲线如图8 所示。其中：横轴表示假阳率（即虚警率），纵轴表示真阳率（即检测率）；实线表示随机猜测，判断载体隐写和未隐写的概率均为50%。ROC 曲线下面积（Area Under ROC Curve，AUC）表征了检测器对此类隐写对象的适用性程度。由图8可知，本文方法在两种隐写算法下的AUC 均大于文献［11］方法，即本文检测器性能更优。

图8 两种深度学习检测方法对LSBM隐写和STC隐写的ROC曲线Fig.8 ROC curves of two deep learning detection methods for LSBM steganography and STC steganography

5 结语

针对现有隐写检测方法对STC音频隐写算法难以检测的问题，本文提出了一种融合深度残差网络和极限梯度提升的音频隐写检测模型ResNet-XGBoost。基于ResNet-XGBoost 模型的音频隐写检测方法首先构建了一种用于提取高维抽象特征的深度残差网络模型，再将利用其提取的特征作为XGBoost 模型的输入进行分类。实验中比较了本文方法和其他四种经典音频隐写检测方法对LSBM 隐写算法和STC 隐写算法的检测准确率，实验结果表明，相较于传统提取手工特征的检测方法和基于深度学习的检测方法，本文方法检测准确率最高且有明显提升。STC 隐写中子校验矩阵高度较高时的检测准确率低于子校验矩阵高度较低时，证明了子校验矩阵高度对隐写检测准确率有直接影响，子校验矩阵高度越高，隐写算法越难以检测。同时，本文方法采用深度残差网络提取高维抽象特征并用XGBoost 模型分类，相较传统的隐写检测方法通常集中于依靠经验设计手工特征，本文方法则从一个新的角度出发提取特征，避免了耗费大量精力着眼于复杂的手工特征设计上。

后续工作将研究基于STC框架的自适应音频隐写的检测算法，考虑到自适应隐写嵌密集中于复杂区域上，研究重点则聚焦于隐写信号的提取和放大，然后采用本文方法进行隐写检测。