线间潮流控制器模型预测控制参数辨识研究

华国武，周渊深，吴迪，王在福，叶青

(1.中国矿业大学 a.电气与动力工程学院;b.信息与控制工程学院,江苏 徐州 221008；2. 江苏海洋大学 电子工程学院，江苏 连云港 220005)

自柔性交流输电系统(flexible AC transmission system，FACTS)被提出，柔性交流输电技术得到了快速的发展。目前柔性交流输电装置已经发展到第三代，其中最具有代表性的装置为统一潮流控制器(unified power flow controller，UPFC)[1]，近年来国内外对UPFC的研究得到了很大的进展，国内首个UPFC工程于2018年在南京西环网得以应用[2]。美国西屋科技的Gyugyi博士在提出UPFC之后于1999年又提出了线间潮流控制器(interline power flow controller，IPFC)技术。与UPFC相比，IPFC性能更为强大，它不仅可以像UPFC一样直接控制目标线路功率，还能同时控制多条输电线路中功率的流动，且UPFC只可以控制1条线路上的功率，而线路有功功率和无功功率可能会超过系统所允许的最大限定值。若线路上的功率超过所承受的极限，电力系统的稳定性和安全性就会受到严重的影响。IPFC控制的线路包含1条从线和多条主线，可以人为地选择多条线路之间的潮流进行控制，将重载线路上的功率按照需求转移至轻载线路上，实现潮流的重新分布[3]。

目前IPFC没有实际投入运行的工程，还处于理论研究状态。根据可检索到的文献可知，目前国内外主要在IPFC对电力系统多目标潮流优化效果[4]、低频振荡的抑制能力[5]、潮流控制能力[6]等方面进行研究，还没检索到有关IPFC系统参数辨识的相关文献。

文献[7]将模型预测电流控制方法应用于电压源逆变器，利用建立准确的数学模型和当前时刻的电压、电流值，预测下一时刻的目标电流值，将电流误差限制在一定范围之内，稳态性和暂态性较好，且电流畸变率低。文献[8]将有限控制集模型预测控制(finite control set model predictive control，FCS-MPC)应用于多种类型的功率变换器，FCS-MPC通过1个价值函数就可以对多个目标进行控制和优化，与模糊控制、经典的PI控制相比较，突出了模型预测原理简单、应用范围广等优点。

模型预测电流控制方法的控制效果好，响应速度快，缺点是控制效果受搭建的系统模型影响，若系统的模型不准确则控制效果也会不准确；因此，为提高系统的控制效果，需要对系统的参数辨识进行研究。

文献[9]将最小二乘法参数辨识应用到静止无功发生器(static var generator,SVG)上，通过将系统检测到的数据转变成最小二乘格式反馈给控制系统，提升了包含SVG电力系统的暂态稳定性，同时提高了控制的精确性。文献[10]为了克服系统参数变化对系统控制效果的影响引入在线参数辨识，因传统递推最小二乘法参数辨识占用存储空间大及旧数据对新数据产生影响，引入带遗忘因子的最小二乘法参数辨识，通过选取不同的遗忘因子提高了系统的控制精确性和参数辨识速度。

为提高系统的响应速度，本文选择将模型预测电流控制方法用于IPFC上。为减少系统内电阻、电感值的变化对系统控制精度、稳定性的影响，引入模型预测在线参数辨识。传统最小二乘法参数辨识具有占用存储空间大、旧数据影响新数据等缺点，本文引入带遗忘因子的最小二乘法对系统进行参数辨识，并通过仿真验证该方法的有效性。

1 IPFC原理

IPFC的控制目标是准确控制多条输电线路的潮流。一般来说，IPFC采用多个连接在同一个直流终端的变流器(voltage source converter，VSC)，每个VSC可以为自己的线路提供串联补偿。因此也可以将IPFC看作是多个串联同步补偿器共用1个公共的直流电容，从而整个系统的有功功率就可以通过公共直流电容从过载线路向欠负载线路进行适当的传输。

N条线路组成的IPFC模型如图1所示，其中：T1、T2……TN为变压器,N为自然数;US为线路发送端电压；Udc为直流母线电压。

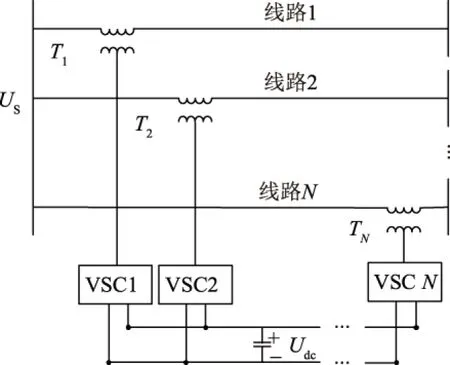
图1 N条线路组成的IPFC模型Fig.1 IPFC model consisting of N lines

N条支路通过1个直流电容连接在一起，直流电容向线路输出任意的有功功率提供能量，每个VSC通过串联变压器输出幅值和相角均可调的电压，相当于在线路上串联1个任意的电压源，该电压源与线路的初始电压相叠加，改变了线路的参数，从而改变线路上的潮流分布。

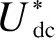
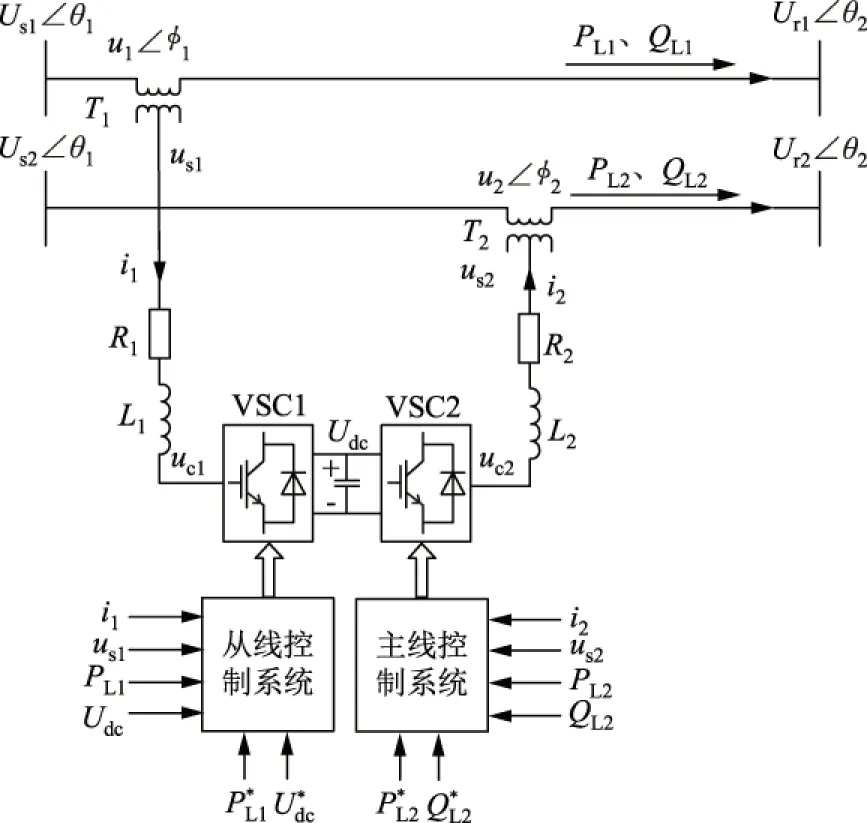
图2 两线路IPFC简化原理图Fig.2 Simplified schematic diagram of two-line IPFC

图2中选择线路1为主线，线路2为从线;重载线路可作为主线进行控制，轻载线路可作为从线进行控制。IPFC的控制目标分为2部分：一部分是控制主线上的有功功率和无功功率跟随目标值；另一部分是控制从线上的有功功率或者无功功率和直流电容电压跟随目标值。直流电容为2条线路双向交换有功功率提供通道，有且仅有有功功率进行交换，且满足功率守恒定律。

IPFC等效电路如图3所示。图3中Pex为两线路交换的有功功率。

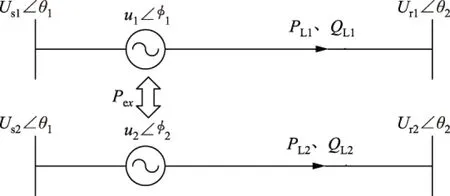
图3 两线路IPFC等效电路Fig.3 Two-line equivalent circuit of IPFC

IPFC主线的补偿方式矢量图如图4所示。图4中：Us为主线发送端电压；Ur为主线接收端电压；δ为发送端和接收端电压相角差；O为坐标原点。补偿区域如图4中虚线圆所示，可以将补偿区域分为4块，当主线路补偿电压矢量在区域Ⅱ时，接收端的有功功率增大，无功功率减小。主线补偿电压矢量在4个不同扇区时对线路功率补偿效果不同，其对主线功率影响见表1[3]。

图4 IPFC主线补偿电压矢量图Fig.4 Master line compensation vector of IPFC

表1 电压不同区域时主线功率变化情况Tab.1 Power changes of the master line in different voltage regions

2 IPFC模型预测控制原理

模型预测控制(model predictive control，MPC)具有原理简单和响应速度快等优点，同时对多变量等问题的控制效果较好，因此MPC近几年已经被成功应用到制造、新能源等领域。

2.1 MPC原理

MPC本质上是一种寻得问题最优解的控制方法，即通过建立模型预测未来时刻系统的所有状态，得到相应状态下的输出结果，通过设置优化目标和约束条件，挑选出使系统控制效果最优的控制方式应用于该系统，从而得到最优的控制效果[11]。

图5所示为VSC通用MPC框图，图5中：x(k)为系统第k次采样的测量值(其他类似参量含义依次类推)；x*(k)为给定值。MPC基本思路为：

a)建立数学模型预测系统变量在某时间段内未来时刻的变化。

b)利用价值函数表示期望的系统行为。

c)利用最小价值函数确定最优的工作方式。

图5 VSC通用MPC框图Fig.5 Block Diagram of general model predictive control of VSC

2.2 基于IPFC的MPC

对于图2所示的两线路IPFC简化原理图，假设系统的三相电压平衡，分别建立主线、从线的数学模型。

IPFC主线的三相输出电压和电流的关系式为：

(1)

式中t为时间。

两相静止坐标系下数学模型为：

(2)

式中us1y(y=α,β)为主线系统在两相静止坐标系αβ下的电压(其他类似参量含义依次类推)。

通过控制VSC三相桥臂的开关状态Sa、Sb、Sc，可以得到主线VSC的输出电压uc1，uc1在两相静止坐标系下的输出电压为：

(3)

式中S1a、S1b、S1c分别为主线VSC三相ABC的开关状态。

欧拉法是一种数值求解方法，为建立系统离散化预测模型通常采用欧拉法对公式进行求解，同时它也是求解常微分方程最基本的方法[12]。欧拉法分为前向欧拉法和后向欧拉法，本文采用前向欧拉法进行求解。前向欧拉法的基本数学表达式为

(4)

式中Ts为采样周期。

两相静止坐标系下主线预测离散时间数学模型为：

(5)

构造主线代价函数可以使实际值紧跟目标值，主线代价函数为

(6)

主线的控制目标为该线路上的有功功率和无功功率。有功功率和无功功率的给定值与相应的测量值之差经过PI控制器输出并经过相应的变化,成为下一时刻的电流给定值。将k次采样的测量值和目标值代入式(5)可以预测得到下一时刻的电流值，将基本电压矢量代入到预测电流表达式中，分别得到不同情况下的代价函数值，代价函数越小表示预测值与给定值之间的误差越小；选择使代价函数最小的对应电压矢量应用到下一时刻的换流器上，这样就能使输出电流紧紧跟随给定值。

对从线的分析与主线类似，从线输出三相电压、电流的关系式为：

(7)

从线电压、电流在两相静止坐标系下的数学模型为：

(8)

从线VSC在两相静止坐标系下的输出电压为：

(9)

式中S2a、S2b、S2c分别为从线VSC三相ABC的开关状态。

两相静止坐标系下从线预测离散时间模型为：

(10)

构建从线代价函数

(11)

从线的控制目标为直流电压和有功功率或无功功率。目标直流电压值和有功功率值与实际值之差经过PI调节器输出并经过相应的变换,成为目标电流值。将k次采样的测量值和目标值代入式(10)可以预测得到下一时刻的电流值，将基本电压矢量代入到预测电流表达式中，得到使价值函数最小的电压矢量，并将该电压矢量应用到下一时刻的换流器上，这样就能使输出电流紧紧跟随给定值。

通过对IPFC主线和从线的预测模型进行分析可知，预测的精确性受系统主线和从线电阻及电感R1、L1、R2、L2影响。在实际应用中系统参数受环境的影响会发生变化，使代价函数不准确，影响电压矢量的选择，从而造成有功功率和无功功率控制不准确。为消除实际值与期望值之间存在的误差，FCS-MPC利用反馈校正环节和滚动优化环节构成系统闭环。反馈校正的形式较多，一般通过参数辨识技术和扰动观测器技术实现，此2种方法校正方式不同，其中参数辨识通过校正系统参数提高系统模型精确度，扰动观测器通过直接对预测值进行补偿提高预测的精确度。扰动观测器技术依赖于系统的数学模型，本文选择通过参数辨识提升系统的控制精确度。

3 IPFC在线参数辨识

选择参数辨识算法需要考虑到辨识精度、收敛性、收敛速度等因素。最小二乘法是比较常见的一种参数辨识法，此方法辨识精度高，容易实现，但是在观测值变多时，所需的存储空间变大，参数的辨识效果变差，同时旧数据对新数据也会产生影响；故引入带遗忘因子的最小二乘法，此时遗忘因子越小，旧数据对新数据的影响越小，跟踪效果越强[13]。

3.1 带遗忘因子的最小二乘法

最小二乘法参数辨识是由数学最小二乘法衍生而来，最小二乘法理论上使参数计算值与系统实际值之间的差值的平方和最小[13]。多次将参数计算值代替估计值就可以准确地得到参数估计值,同时通过合理设置影响因子来削弱旧数据对新数据的影响。遗忘因子的取值范围一般为0.8～1.0，当遗忘因子为1.0时就变成了普通最小二乘法，遗忘因子越小跟踪能力越强，但是遗忘因子过小会使参数估计过程产生较大波动[14-17]。

带遗忘因子的递推最小二乘法的方程为[18]：

(12)

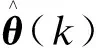
3.2 IPFC参数辨识过程

将主线预测离散模型改成最小二乘格式[19-20]：

i1α(k)=X1i1α(k-1)+

Y1(us1α(k-1)-uc1α(k-1)).

(13)

相对于式(12)，此时有：

(14)

主线的参数辨识过程如下：

b)采集当前时刻的观测值φ(k)代入到式(12)计算出P(k);

c) 按照式(12)得到K(k);

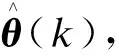
e)进入下一周期，重复b)、c)、d)过程。

从线的参数辨识过程与主线类似，因此不做详细分析，只列出从线最小二乘格式。从线预测离散模型的最小二乘格式为

i2α(k)=X2i2α(k-1)+

Y2(uc2α(k-1)-us2α(k-1)).

(15)

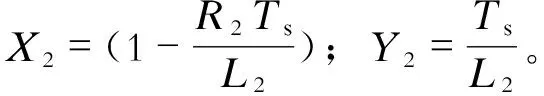
相对于式(12)，此时有：

(16)

4 仿真验证

为了验证本文所用控制策略的有效性，基于MATLAB/Simulink进行仿真验证，系统的仿真参数见表2。表2中δ1、δ2分别为主线和从线发送端和接收端电压相角差。

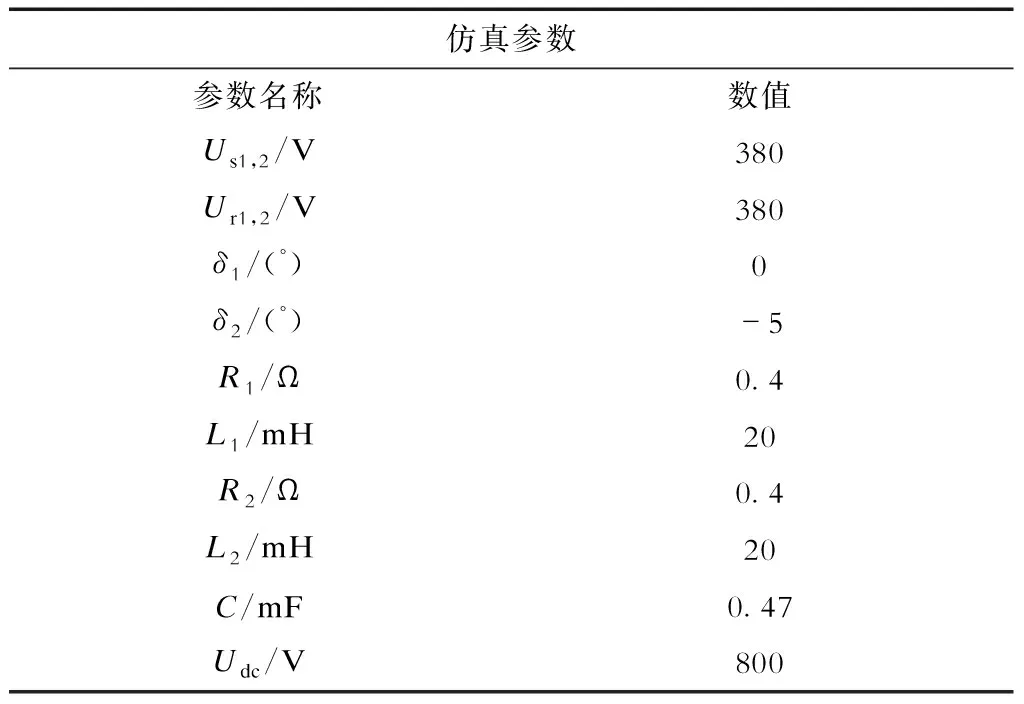
表2 仿真参数Tab.2 Simulation parameters

以主线辨识为例，主线电阻、电感的初始参数(铭牌值)与实际参数不同，R1初始值为0.25 Ω，电感初始值为15 mH，R1实际值为0.4 Ω，电感实际值为20 mH，造成参数失配。在未加入参数辨识之前一直是将系统的电阻、电感初始值代入预测模型，预测输出的目标电流值存在较大误差；在0.2 s之后加入参数辨识，根据输入到参数辨识模块的电压、电流等一直循环辨识出实际电感、电阻值，通过输出的功率波形可以看出加入辨识之后的功率更加准确。

主线的目标有功功率为2 kW、无功功率为-3 kvar，从线的目标有功功率为3 kW、直流电压为800 V。在0.2 s时采用参数辨识，影响因子λ取0.96。图6为主线输出电压us1a、电流i1a参数辨识前后波形；图7为从线输出电压us2a、电流i2a参数辨识前后波形；图8为主线输出有功功率P1、无功功率Q1参数辨识前后波形；图9为从线输出有功功率P2参数辨识前后波形;图10为直流电压Udc参数辨识前后波形。

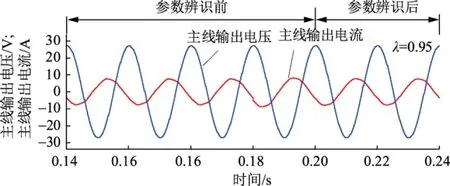
图6 主线输出电压、输出电流波形Fig.6 Waveforms of us1a，i1a of the master line

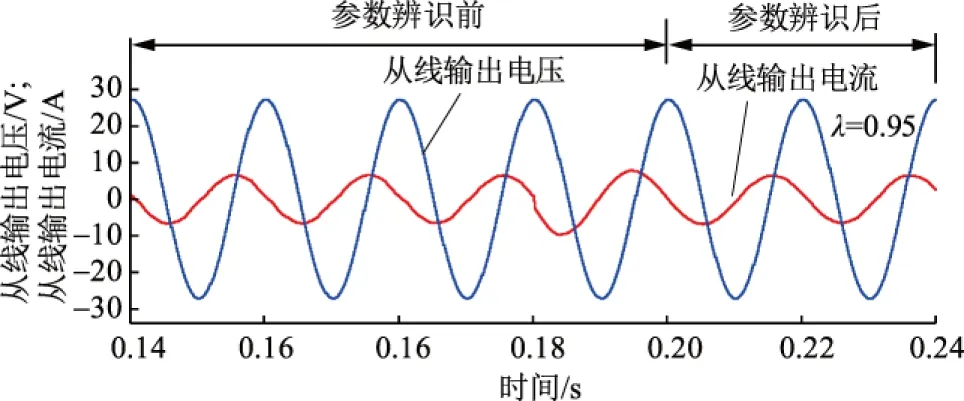
图7 从线输出电压、输出电流波形Fig.7 Waveforms of us2a，i2a of the slave line

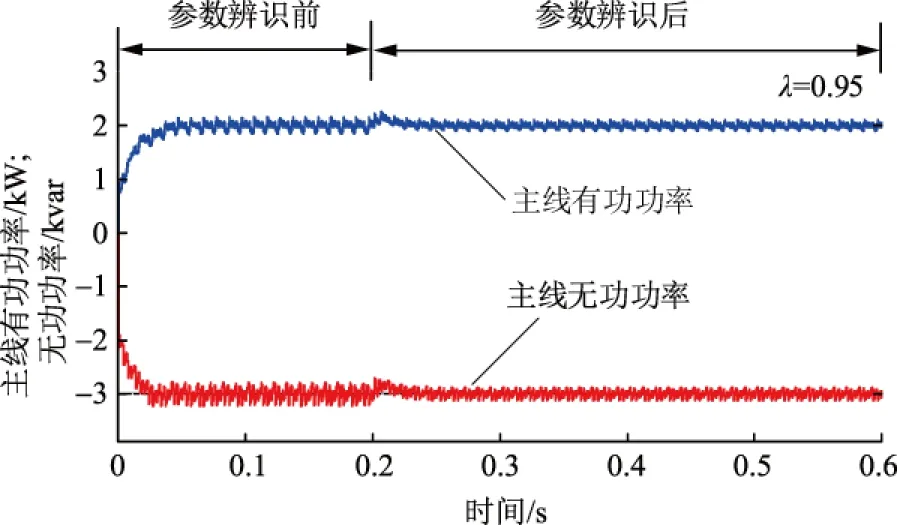
图8 主线P1、Q1波形Fig.8 Waveforms of P1、Q1 of the master line

由图6至图10可以看出：在0.2 s时加入在线参数辨识后输出功率变得更准确，且输出电流畸变率低，直流电压保持稳定、误差小。

图11、图12分别为遗忘因子不同时的最小二乘法主线电阻R1、主线电感L1在线辨识结果波形，图13、图14分别为采用传统最小二乘法时主线电阻R1、电感L1在线参数辨识结果波形，图15、图16分别为遗忘因子不同时的最小二乘法从线电阻R2、从线电感L2在线辨识结果波形，图17、图18分别为采用传统最小二乘法时从线电阻R2、电感L2在线参数辨识结果波形。

图9 从线P2波形Fig.9 Waveform of P2 of the slave line

图10 直流电压波形Fig.10 DC voltage waveform

图11 不同遗忘因子的最小二乘法下主线电阻的辨识结果Fig.11 Identification results of the master line resistance under different forgetting factors

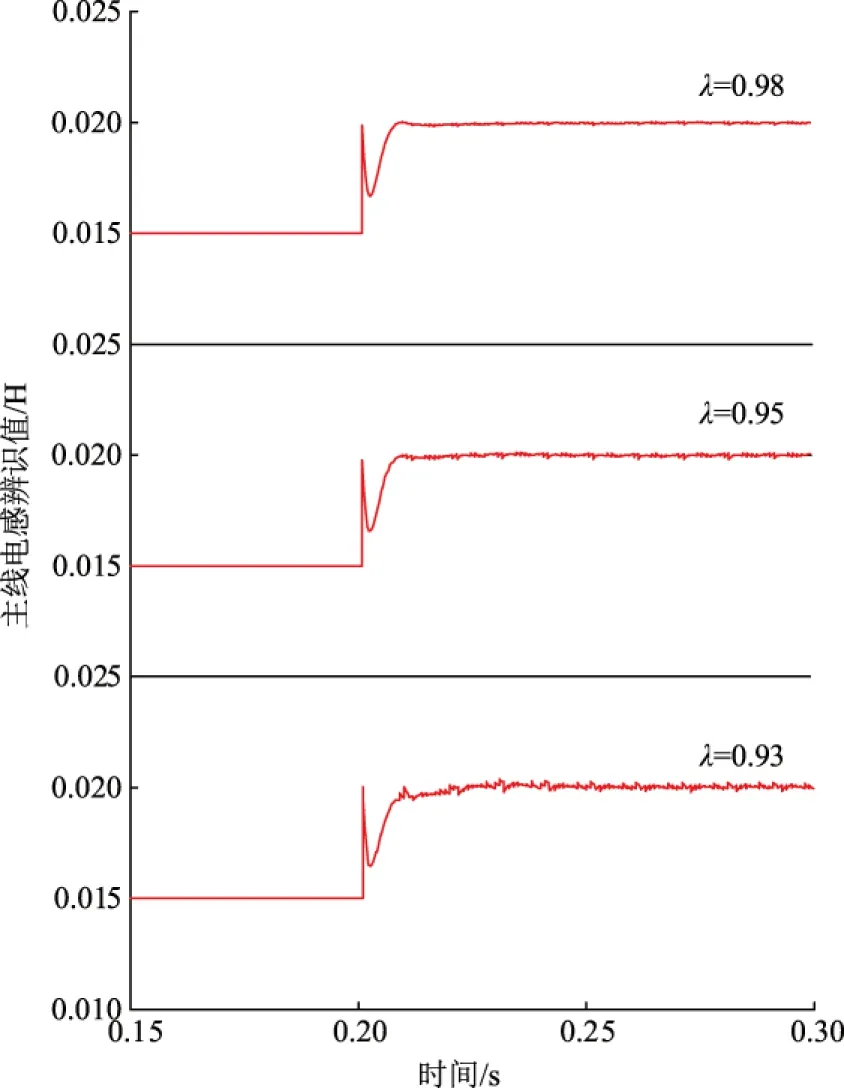
图12 不同遗忘因子的最小二乘法的主线电感的辨识结果Fig.12 Identification results of the master line inductance under different forgetting factors

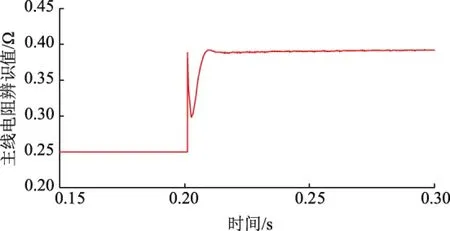
图13 传统最小二乘法下主线电阻的辨识结果Fig.13 Identification results of the masterr line resistance under traditional recursive least squares method

图14 传统最小二乘法下主线电感的辨识结果Fig.14 Identification results of the master line inductanceunder traditional recursive least squares method

图15 不同遗忘因子的最小二乘法下从线电阻的辨识结果Fig.15 Identification results of slave line resistance under different forgetting factors

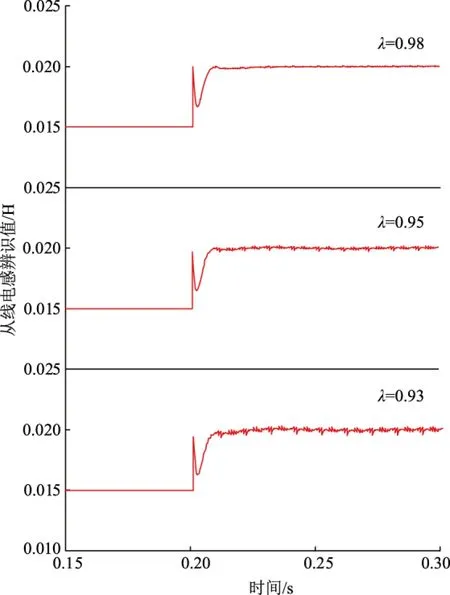
图16 不同遗忘因子的最小二乘法下从线电感的辨识结果Fig.16 Identification results of slave line inductance under different forgetting factors

由图11至图18辨识结果可知：带遗忘因子的最小二乘法参数辨识在识别速度上快于传统最小二乘法，传统最小二乘法的辨识结果受旧数据的影响易饱和，辨识结果有一定的误差；带遗忘因子的最小二乘法通过对遗忘因子的选择可以削弱旧数据对新数据的影响。遗忘因子的选择范围一般为0.8～1.0，遗忘因子较小时，参数辨识的速度快，但是辨识波形波动较大；遗忘因子较大时，参数辨识能力较弱。

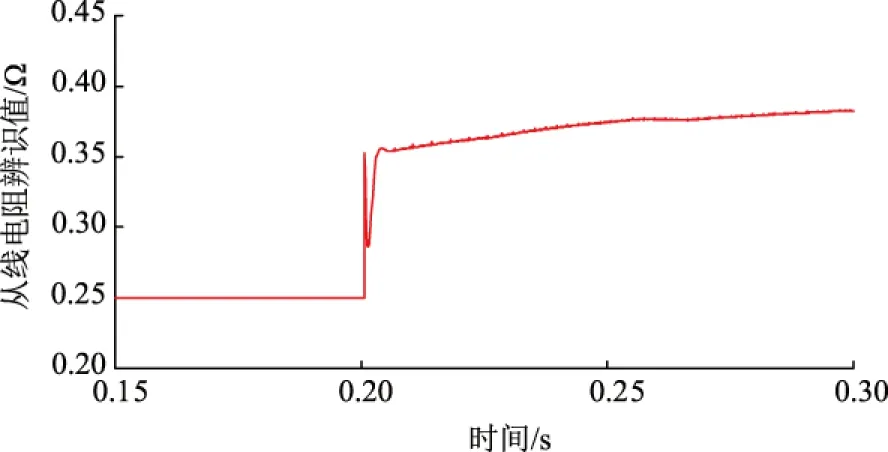
图17 传统最小二乘法下从线电阻的辨识结果Fig.17 Identification results of slave line resistance under traditional recursive least squares method

图18 传统最小二乘法下从线电感的辨识结果Fig.18 Identification results of slave line inductance under traditional recursive least squares method

5 结束语

模型预测具有原理简单、动态响应快、应用范围广等优点，本文选择将模型预测电流控制用于IPFC上。但是该控制策略依赖于准确的数学模型，为消除系统内电阻、电感参数的变化对系统控制精度、稳定性的影响，引入模型预测在线参数辨识。针对利用传统最小二乘法进行参数辨识计算量大、跟踪能力差等缺点，引入带遗忘因子的最小二乘法对系统进行参数辨识。遗忘因子越小，参数辨识过程波动越大，速度越快；遗忘因子越大，辨识结果误差越大，速度越慢。通过对遗忘因子的选择可以提高系统响应速度，降低电流畸变率，得到准确的系统辨识参数。