基于PCA-CLEAN的输电杆塔形变预测方法

2021-03-06陈远刘佳黄林超林丽梅

广东电力 2021年2期

陈远，刘佳，黄林超，林丽梅

(南方电网数字电网研究院有限公司，广东广州 510000)

输电杆塔作为输电线路中的关键一环，对保障电力能源的安全可靠传输具有重要意义。输电杆塔通常布置在室外环境中，长时间受风吹日晒、雨雪冰雹以及地壳运动等因素影响，会出现不同程度的倾斜、形变、螺栓松动等问题，给电力系统的安全稳定运行带来隐患[1-3]。目前采用的人工巡检方式存在主观性强、精度低等问题，并且在极端天气和恶劣环境下巡检人员的人身安全难以保证，不能满足实时监测的要求[4]。

随着智慧电力技术的发展，近年来一些输电杆塔自动形变监测方法逐渐开始代替传统人工巡检方式[5]。文献[6]提出在电力塔杆上安装二维倾角测量传感器，根据测量得到的横向和顺线方向倾角变化计算出输电杆塔的姿态，从而实现自动形变监测，但是该类方法无法监测塔基基础平面的平移滑动情况；文献[7]在输电杆塔塔基周围安装测斜管，通过监测测斜管内高度传感器获得的倾角信息对塔基的形变趋势进行分析，但是这种方法施工难度较高，并且测量精度受制于测斜传感器的精度和成功率。基于北斗卫星导航系统(以下简称“北斗”)/GPS对输电杆塔进行实时监测具备全天时、全天候、操作简单和低成本等优势，一经提出便迅速成为研究的热点，该类方法的基本思想是利用北斗/GPS系统的差分定位技术，对输电杆塔的三维形变进行实时、高精度监测[8]。文献[9]通过在输电杆塔上安装监测设备获取差分信息，然后利用北斗接收机对差分信息进行高精度定位解算，从而获取塔杆的倾斜状态，从而实现实时预警；文献[10]研发了基于北斗及GPS双系统的输电杆塔滑移监测系统，获得了高达厘米级的定位精度。上述基于北斗/GPS的输电杆塔形变监测系统在设计过程中都假设测量环境是理想的，但在实际工程实践中，受森林、山脉、建筑物等影响，北斗/GPS接收机接收到的信号中不可避免地存在多径信号，使得形变监测精度下降。

本文在前述研究的基础上，针对利用北斗系统进行输电杆塔形变监测过程中存在的多径信号问题，提出基于主成分分析(principal component analysis，PCA)和CLEAN算法的多径信号抑制方法。首先利用PCA对接收信号进行分析，自动确定信号中多径信号个数，在此基础上利用CELAN算法剔除其中的多径信号和噪声；然后针对传统BP神经网络预测模型受参数初值选取影响较大的问题，提出遗传模拟退火(genetic simulated annealing，GSA)优化算法，对BP网络初值进行优化，确保其收敛于全局最优解；最后，采用仿真试验对所提方法的有效性进行验证。

1 基于CLEAN算法的多径抑制

1.1 多径模型

在卫星导航系统中，多径信号与星座布局、系统所处环境、接收机性能等多种因素有关，接收机很难将同时接收到的直达信号和多径信号分离开，接收机实际接收到的信号可表示为

r(t)=s(t)+sd(t)+n(t)=

Ap(t-τ0)exp(jωt)+

(1)

式中：s(t)为直达信号；sd(t)为M路多径信号；αm、τm、θm为第m路多径信号相对于直达信号的振幅衰减因子、延时及相位差；p(t)为发射信号；A和τ0分别为直达信号的幅度和延时；ω为载波角频率；n(t)为噪声，通常认为其服从高斯分布。

进行信号检测时，接收机内复制的超前支路和滞后支路码片序列可以表示为：

(2)

式中：φc为多径信号引起的载波相位误差；δP和δD分别为锁相环和延迟锁定环的跟踪误差；Δ为码间距；ω1为本振信号角频率。利用超前和滞后支路码片序列与式(1)，得到输出信号分别为：

(3)

式中：Rp(t)和Rc(t)分别为直达信号和伪码的自相关函数；φ0、φm和φ0、φm分别为超前码和滞后码与直达信号和多径信号的相位差；fc和Tc分别为频差和积累时间；a和τj分别为接收处理引起的幅度衰减和延时。由式(3)可以看出，多径信号的存在导致输出信号自相关函数发生畸变，从而影响卫星导航系统的定位精度。

1.2 CLEAN算法

CLEAN算法最早由Hogbom于1974年提出，用于抑制射电天文综合孔径成像中包含的旁瓣信号，改善成像质量。CLEAN算法能够从复杂信号中提取特定频率分量，被广泛应用于非平稳、非线性信号分析[11]。利用CLEAN算法对任意时间信号δ(t)进行分析并提取特定频率分量的步骤如下：

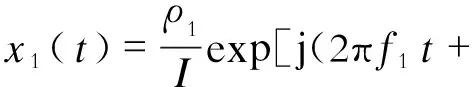
步骤4，计算剩余信号，从原始信号中减去步骤3中得到的最大幅度信号分量，得到剩余信号δres(t)=δ(t)-x1(t)；

步骤5，令σres(t)作为初始信号δ(t)，重复步骤1至步骤4，依次提取初始输入信号中的K个最大幅度信号分量xk(t),k=1,2,…,K。

经CLEAN分解后，原始信号可以表示为

(4)

从上述分析可知，利用CLEAN算法对形变监测信号进行分解，其依次提取的K个最大幅度信号中，第1个为直达信号，其余K-1个为多径信号，即式(1)中M=K-1。

1.3 K值确定

CLEAN算法在使用过程中的核心问题是确定K值，常用的经验试错法存在主观性强和运算量大的问题。PCA是数据处理领域中经典的信息提取和数据降维方法，该方法将待处理数据按所含信息的相关性划分为不同的簇，进而将每一簇内的信息综合成为1条主信息，不同簇之间的主信息相互正交，在实现减少需要分析处理信息量的同时保留数据中的绝大部分信息。对于W维数据，PCA首先提取数据中方差最大的方向，然后提取与其正交平面中方差最大的方向，依次类推，直至提取K个方差较大的方向后，剩余W-K个方向的数据方差很小可以忽略，此时K个主方向张成的空间中包含了W维数据中的绝大部分信息，从而实现数据降维[12-14]。

本文将PCA与CLEAN算法结合，利用PCA对原始信号进行特征分解，根据大特征值个数确定K值。对于式(4)所示信号，其协方差矩阵可以表示为：

Rpp=Rxx+σ2I.

(5)

式中：Rpp为原始信号协方差矩阵；Rxx为谐波分量对应的协方差矩阵；σ2I为噪声对应的协方差矩阵。对Rpp进行特征分解，得到特征向量和特征值分别为ui和λi，i=1,2，…，W；表达式如下：

(6)

对分解结果进行分析可以发现，前K个特征值远远大于剩余W-K个特征值，这是由于前K个特征值对应特征向量构成的信号子空间可以描述信号中的谐波分量，剩余W-K个小特征值对应特征向量构成的噪声子空间用于描述信号中的噪声。本文定义占特征值谱总能量95%的大特征值个数为K，即

(7)

由式(5)和式(6)可知：当数据中包含零均值高斯白噪声，并且噪声与信号分量相互独立时，经PCA特征分解后，噪声数据协方差矩阵为对角阵，特征值明显小于信号分量特征值，通过剔除小特征值对应的特征向量即可实现噪声抑制(数据降维)，但是PCA无法实现对多径信号的抑制。采用CLEAN算法进行数据降维不仅适用于上述高斯白噪声，也适用多径信号等噪声。然而正如前文提到的，CLEAN算法进行数据降维时需要预先知道信号分量个数，否则会由于无法确定CLEAN算法迭代终止条件而不能有效达到数据降维的目的。

本文将PCA方法与CLEAN方法结合起来，首先利用PCA对数据进行特征分解，得到大特征值个数即为数据中信号分量个数，然后将其作为CLEAN算法的先验信息，从而利用CLEAN算法同时实现对数据中高斯白噪声和多径信号的抑制。

2 预测模型设计

2.1 BP神经网络

神经网络模型具备对任意非平稳、非线性函数的逼近能力，适合对输电杆塔形变进行预测，而BP神经网络是目前应用最广、理论最成熟的神经网络模型；因此本文采用BP神经网络来构建输电杆塔形变预测模型。图1所示为典型的3层BP网络拓扑结构，由输入层、隐含层和输出层组成。BP神经网络内信号的传输包含输入层经隐含层向输出层传播的正向传播，以及输出误差通过隐含层流向输入层的反向传播，经过正向传播和反向传播的反复迭代，模型的权值不断朝向误差减小的方法优化[15-16]。

图1 3层BP网络架构Fig.1 Three-layer BP network framework

假设zr(r=1,2,…,N)为BP网络的N个输入神经元，由输入到输出的正向传播过程可以表示为

(8)

式中：hrj为连接输入层与隐含层的权值；wjg(j=1,2，…，l；g=1,2，…,G)为连接隐含层与输入层的权值，l和G为隐层节点数和输出节点数；χj为阈值；f(·)为激活函数。

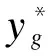
(9)

传统BP神经网络对权值和阈值的优化采用的是梯度下降法，其性能受参数初值的选取影响较大，并且容易陷入局部极小值。例如在如图2所示的优化问题中，存在唯一的全局最小值C，如果迭代开始时，参数初值选在e点或f点，则根据梯度下降算法可以得到最优解，但是如果迭代开始时参数初始值选在a、b、c或d点，则迭代终止时，模型会陷入局部极小值A和B，无法实现全局最优。因此需要一种全局优化算法对BP神经网络的参数初值进行优化，确保模型最终收敛于全局最优解。

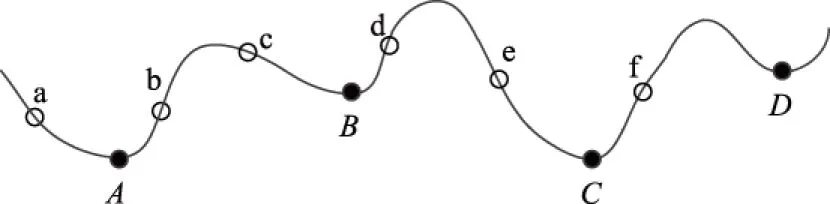
图2 存在局部极小值时的优化问题示意图Fig.2 Schematic diagram of optimization with local minimum value

2.2 GSA-BP神经网络

遗传算法(genetic algorithm，GA)和模拟退火算法(simulated annealing，SA)是当前在优化理论中应用非常广泛的2种随机搜索算法，GA通过“选择”“交叉”和“变异”操作对达尔文生物进化论中的自然选择模型进行抽象描述，算法的每次迭代都会选择更适合当前环境的生物集合(参数集合)，直至获取全局最优解。GA具有较强的全局搜索能力，但是局部搜索能力较差。而SA模拟的是自然界中固体物质退火的过程，其优势是收敛速度快，局部搜索能力强，并且根据Metropolis准则，SA具备跳出局部最优解的能力，但是SA的全局搜索能力较差[17]。

在已有研究的基础上，本文提出一种遗传模拟退火算法(genetic simulated annealing，GSA)，对BP网络的初值进行全局寻优。首先利用GA全局搜索能力强的特点对BP网络初值进行寻优，将得到的当前最优解作为SA的初始值；利用SA在当前最优解附近进行局部搜索，得到满足Metropolis准则的新解；进而将其作为下一轮迭代中GA的初始种群，经过多次全局搜索和局部搜索的交替迭代最终获得全局最优解；最后利用最优解构建BP网络模型对输电杆塔形变进行预测。所提GSA-BP算法流程如图3所示，具体步骤如下：

步骤1，根据所要描述的具体问题对初始化BP网络的网络层数，输入和输出神经元个数和隐层节点数。

步骤2，将BP网络权值和阈值作为GA的初始种群，并对其编码。

步骤3，对当前种群进行选择、交叉和变异操作，得到当前条件下的最优种群。

步骤4，将步骤3得到的最优种群作为SA的当前初始解。

步骤5，SA模拟退火操作，包括：①根据当前解计算SA的适应度函数；②对当前解叠加随机扰动得到新解，并计算新的适应度函数；③利用Metropolis准则判断是否接受新解；④判断是否满足SA终止条件，若不满足则降温，循环模拟退火操作，满足则将SA得到的新解作为GA的初始种群，并转至步骤2。

步骤6，迭代终止后，将最优权值和阈值赋予BP神经网络进行预测。

图3 GSA-BP算法流程Fig.3 GSA-BP algorithm flowchart

2.3 算法总结

对所提PCA-CLEAN多径抑制方法和GSA-BP预测模型的算法流程进行总结，得到如图4所示的算法思维图。首先利用PCA对历史形变数据进行分析，并按照式(7)计算得到大特征值个数K，将其作为CLEAN算法的先验信息对历史数据进行分解(将其分为噪声、多径信号和直达信号3部分)；然后将直达信号作为输入对GSA-BP模型进行训练和学习，得到最优BP网络参数。由于输电杆塔所处环境在短时间内不会发生剧烈变化，多径信号数量通常较为稳定，因此训练阶段获得的多径信号数量和最优BP网络参数可以作为预测阶段的先验信息，并作为最优模型实现对未来形变趋势进行预测。

图4 所提算法思维图Fig.4 Mind map of the proposed algorithm

3 试验及结果分析

3.1 PCA-CLEAN多径抑制试验

为了验证所提PCA-CLEAN方法的多径抑制性能，对某输电杆塔处2台北斗接收机在2013年1月至2015年6月的数据进行分析，其中一台接收机固定在无遮挡的开阔场地作为基准站，另一台接收机固定在输电杆塔上，两站之间的基线为5.8 m，可消除卫星钟差、轨道误差等与空间相关的误差，由于X、Y和Z方向上的变化基本一致，本文以Y方向为例进行分析。图5给出了对应的接收信号，采样间隔为1 s，其中横坐标为采样时间，纵坐标为归一化信号幅度值。

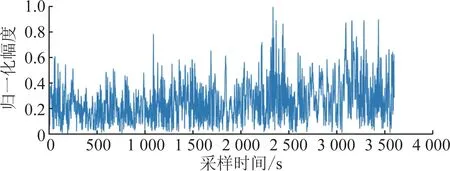
图5 Y方向监测序列Fig.5 Monitoring sequence in Y direction

利用前述PCA方法对图5所示数据进行分析，得到的归一化特征值谱如图6所示，其中横坐标为特征值序号，纵坐标归一化特征值。由图6可以看出前2个特征值较大，从第3个特征值开始急剧减小，按照式(7)可以计算得到大特征值个数为3。在此基础上，利用CLEAN算法对图5数据进行分析，依次提取得到的3个最大幅度信号分别如图7(a)、(b)和(c)所示，其中横坐标为采样时间，纵坐标为归一化信号幅度值。由图7可以看出：最大幅度信号相对于原始信号更加平滑，较好地反映了信号变化趋势，由于直达信号相对于多径信号的传输距离较短，因此直达信号应为第1个最大幅度信号，另外2个幅度较小的信号为多径信号。

图6 特征值谱图Fig.6 Eigenvalue spectrum diagram

3.2 GSA-BP形变预测试验

对上述形变数据进行解算可以得到输电杆塔倾斜度数据，见表1。相邻2期数据的采样间隔为1个月，为了验证所提GSA-BP模型的预测精度，试验过程中，将1～20期数据作为训练样本用于GSA-BP模型的训练，剩余21～30期数据作为测试样本，对GSA-BP模型的预测能力进行评估。采用均方误差作为定量评价指标：

(10)

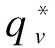
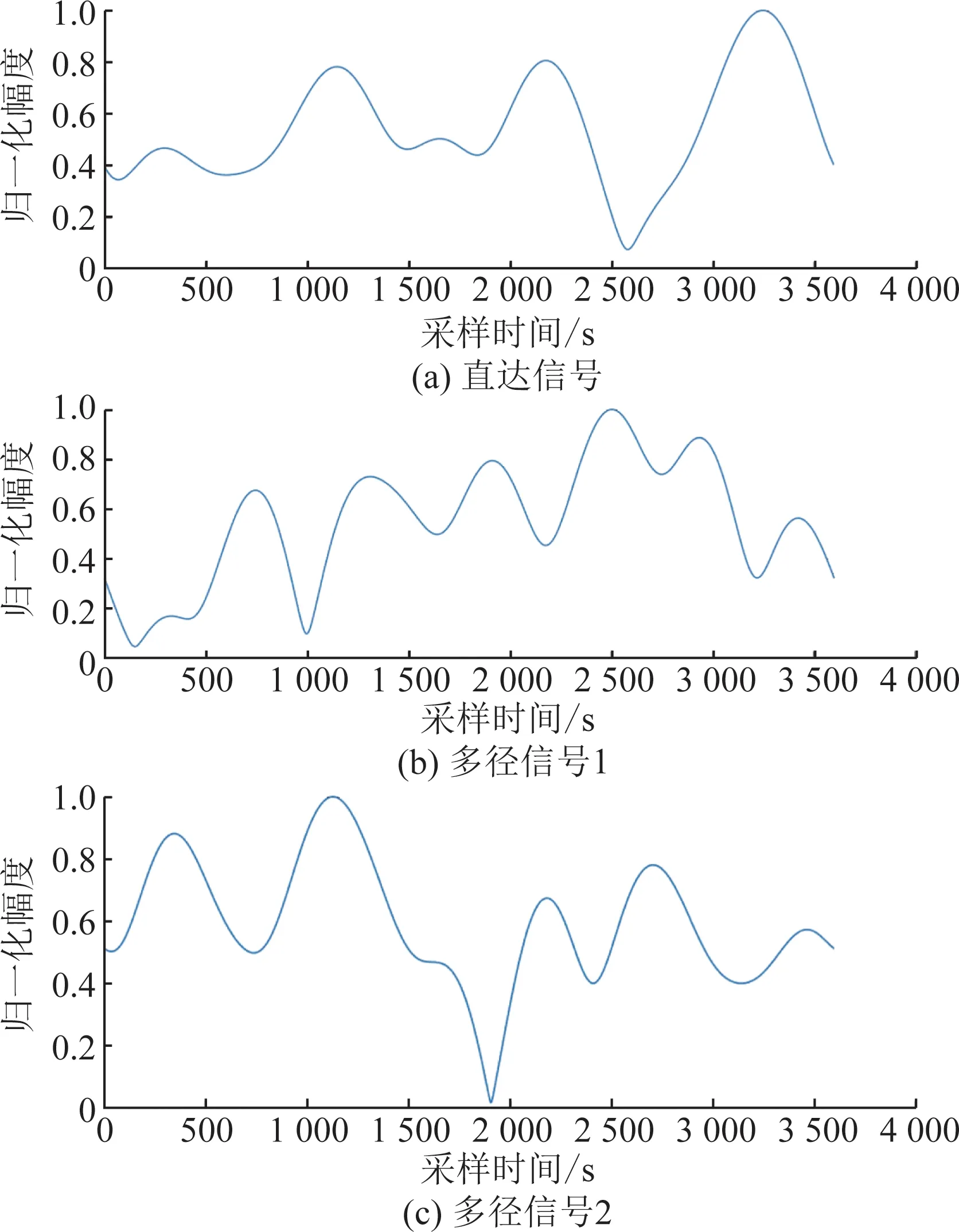
图7 CLEAN算法依次提取的3个最大幅度信号Fig.7 Three signals with maximum amplitudes extracted by CLEAN algorithm in sequence

表1 2013年1月至2015年6月30期倾斜度数据Tab.1 Gradient data from January in 2013 to June 30 in 2015

表2给出了利用所提方法(记为PCA-CLEAN+GSA-BP)的预测结果，其中采用3层BP网络结果，GSA算法的初始种群为初始参数集合C=[w,ω,θ]，3个参数取值的上限为Cmax=[100, 100, 10]，下限为Cmin=[0.1, 0.1, 0.01]。为了对比，给出在相同条件下直接采用GSA-BP以及采用卡尔曼滤波方法得到的结果。

由表2可以证明，在最小误差、最大误差和误差均方根3个维度，所提方法均可以获得最优预测性能。

表2 不同方法的倾斜度预测结果 Tab.2 Predictive results of gradient by different methods %

在实际工程实践中，有时难以获取较多的训练数据，此时希望形变预测方法在较少训练样本条件下，对未来较长时间的形变趋势给出较高精度预测结果，接下来对3种方法在小样本情况下的预测性能进行评估。采用表3中的5种划分方式对数据集进行划分，其中训练样本用于完成模型的训练，测试样本用于验证不同模型的预测性能。

表3 数据集的不同划分方式Tab.3 Different classification ways of data set

表4给出了5种划分方式下3种方法得到预测结果的最小误差、最大误差和误差均方根，由表4可以看出随着训练样本减少及测试样本增多，3种方法的预测性能都出现了不同程度的下降，但是所提方法在5种数据划分方式下均可以获得最优的预测性能。结果表明，在小样本情况下进行长时间预测时，所提方法具有最优的预测性能和鲁棒性，适合于实际工程应用。

4 结束语

随着北斗定位技术的发展，其在电力系统中的应用也越来越广泛，然而由于多径信号的存在，利用北斗系统进行输电杆塔形变预测得到预测结果的精度较低。针对该问题，本文提出基于PCA-CLEAN和GSA-BP网络模型的输电杆塔形变预测方法，首先利用PCA-CLEAN方法对北斗接收机接收到的多径信号进行抑制，然后利用GSA-BP网络模型基于输电杆塔历史形变数据对未来形变趋势进行预测。试验结果表明，所提方法相对于GSA-BP和卡尔曼滤波方法的预测精度分别提升62%和71%，具有较强应用前景。