基于带时间尺度PCA-RBF的脱硝系统入口NOx质量浓度软测量技术

雷志伟

(中国大唐集团科学技术研究院有限公司华东电力试验研究院，安徽 合肥 230031)

选择性催化还原(selective catalytic reduction，SCR)脱硝系统具有大惯性、强时延的特点[1-3]，当机组运行工况大范围变化时，根据入口NOx质量浓度可以提前预测出口NOx质量浓度的变化，并及时控制以抑制NOx质量浓度的波动[4]。然而，烟气排放连续监测系统(continuous emission monitoring system，CEMS)测量仪表普遍存在测量迟延、测量仪表需不定期反吹等缺点，严重影响了燃煤电厂脱硝自动控制的品质。因此，如何获取高精度、可靠性强的SCR系统入口NOx质量浓度已经成为当前脱硝自动控制领域的热点研究问题之一[5]。翁建国[6]等人采用支持向量回归(support vector regression，SVR)、人工神经网络(artificial neural network，ANN)等建模方法，建立了SCR系统入口NOx质量浓度软测量模型，但SVR、ANN的模型结构较为复杂，难以在生产现场推广应用；陈荣超[7]通过锅炉燃烧热平衡和物料平衡计算，采用数据拟合的方式获得入口NOx质量浓度预测值，虽取得了一定成效，但是过分依赖热平衡和物料平衡计算精度，对不同燃煤机组的普适性不高。

虽然软测量技术可以通过间接变量来预测目标值，但是其建模过程严重依赖样本数据的选择和处理，一旦样本数据量庞大且干扰项较多，将会极大地增加软测量模型结构，使得建模过程十分复杂和漫长，甚至难以达到收敛。国内外建模方法的研究大多侧重于模型结构设计，很少从建模样本处理方面进行研究。因此，本文从建模样本处理方法着手，根据燃煤电厂NOx的产生机理，确定SCR系统入口NOx质量浓度的影响因子。采用主元分析(principal components analysis，PCA)及过程变量(T2统计量)监测，对NOx生成量的主要影响因子进行分析、粗筛，获得若干个关键变量[8-10]；提出时间尺度分析法，计算各个关键变量与测量目标值在不同时间尺度下的相关程度，按照时间尺度对数据样本进行处理，作为径向基函数(radial basis function，RBF)神经网络的训练样本；利用梯度下降法训练规则对RBF神经网络进行训练，提高模型的收敛速度。通过本文的研究，建立一种带时间尺度的PCA-RBF模型，以提高模型预测精度和泛化能力。

1 SCR系统入口NOx质量浓度影响因素分析

燃煤电厂锅炉燃烧过程中会产生大量的NOx，一般可分为热力型NOx、快速型NOx和燃料型NOx。影响这3类NOx生成量的因素与煤质成分、煤量、炉膛燃烧工况、过剩空气系数[11]密切相关，具体表现为机组在升降负荷、深度调峰、配煤掺烧、启停磨煤机组等典型工况下，入口NOx质量浓度大幅度波动，造成SCR脱硝自动控制系统的扰动，从而影响机组NOx排放。

a)各台磨煤机瞬时煤量。煤粉中的氮化物燃烧后生成燃料型NOx，约占炉膛燃烧产生NOx总量的75%～80%，煤量的变化直接关系到入口NOx质量浓度。目前，燃煤电厂大多采用配煤掺烧的方式，各台磨煤机配备不同的煤种，导致各台磨煤机对入口NOx质量浓度的影响不尽相同。

b)过剩空气系数[12-13]。过剩空气系数与总风量、总煤量密切相关。过剩空气系数增加会导致燃料型NOx的生成量增多，同时也会因炉膛燃烧区域温度升高造成热力型NOx增加，富氧环境一定程度上还会阻碍NOx的还原。

c)磨煤机组合方式。磨煤机一般按上、中、下3层布置，不同层磨煤机的启停过程对炉膛燃烧工况的改变有很大的影响，造成炉膛火焰中心偏移，改变炉膛燃烧温度，影响NOx的生成量。启停磨煤机时风、煤的控制时间有先后，炉膛中的氧量则因此在短时间内突增突降，势必会增加对NOx质量浓度的扰动。

综上，以某型机组为例，从锅炉燃烧、机组运行工况等主要参数中选取27个原始变量来构建SCR系统入口NOx质量浓度软测量模型参数，见表1。

表1 软测量模型原始变量Tab.1 Initial variables of soft measurement model

2 入口NOx质量浓度影响因素分析

构建软测量模型需要采用大量的间接变量，为了精简网络模型，提高模型测量精度，通常需要对原始变量进行数据筛选、分析，以降低网络结构设计的复杂度[14]，以便于实际工程应用。本文采用PCA和T2统计量监测[15]对原始变量进行降维筛选，目的是寻找到与软测量参数相关性大的初选变量，剔除相关性较小的变量，从而减少神经网络模型的输入参数[16]，有助于网络模型训练和收敛，提高模型的泛化能力。

同时，由于各个初选变量与NOx质量浓度的相关程度在时间尺度上不尽相同，即各个变量对NOx质量浓度的影响时刻不同，利用时间尺度分析法计算初选变量与测量目标值在不同时刻下的相关性指标，确立各个初选变量的时间尺度，经数据处理后作为RBF神经网络模型的输入，能够提升软测量模型的测量精度，降低建模复杂度。

2.1 PCA和T2统计量监测

设原始变量的数据样本集为X，则

(1)

式中：xi,j为样本集中第i个变量的第j个数值；M为变量数；N为样本总数。

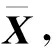
(2)

进一步将协方差矩阵H分解为

COV=P∑PT.

(3)

式中：P=[p1p2…pi…pN]为酉矩阵，pi为主元的负荷向量；Σ为对角线上元素为特征值、其他元素均为0的矩阵，记为

通过对比各个主元贡献率的大小，建立主元模型。若前k个主元的贡献率之和满足要求，则原始样本就可以采用主元模型代替，并将原始样本维数压缩至k维，即

(4)

T2统计量由得分向量Tk在变换后空间中的马氏距离计算得出，T2统计量反映了当前数据偏离数据中心的程度[17]，其计算公式为

(5)

可以采用直方图直观辨别每个原始变量对当前时刻T2统计量的贡献值，进而得出各个变量对主元的贡献量，最后筛选出主要影响因素。

2.2 时间尺度分析

由式(1)选取出的k个主导变量Xk={xg|g∈[1,k]}，计算各个主导变量的均值，记为Fg。

定义各个主导变量与目标变量y之间的相关性指标，记作S，计算公式为

(6)

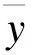
若存在一个b，bN*，使得S达到最小，则表示主导变量xg与目标变量y在时间尺度b上相关性最大。按照各个主导变量与目标变量的时间尺度关系，对各个主导变量进行时间移位处理，构建带时间尺度的数据样本。

2.3 梯度下降法RBF神经网络模型

RBF神经网络[17]具有万能逼近任意连续函数的特点，本文采用RBF网络结构，建立SCR系统入口NOx质量浓度软测量模型。RBF神经网络由3层结构组成，为输入层、隐含层和输出层。输入层的个数由选取的软测量变量数决定，隐含层根据模型收敛速度设定，一般需要通过多次调整。

设计一个k-h-1结构的RBF网，其中h为隐节点个数，其激活函数一般采用Gaussian型RBF，隐含层输出矩阵[18]

(7)

式中：Xk、C为RBF隐含层数据中心；r为隐含层的扩展常数向量。

输出层的传递函数只需要采用线性函数即可，RBF网模型输出

G=W·ΦT，

(8)

式中W为隐含层输出权值矩阵。

梯度下降法适合于大容量数据样本的RBF神经网络训练[19]，神经网络的输出矩阵G与目标变量矩阵Y的误差记为

(9)

网络学习的方向就是梯度下降的方向[20-21]，训练过程就是权值不断通过误差梯度修正，数据中心c和隐含层输出权值w的更新公式为：

(10)

(11)

通过反复循环更新，利用误差E的梯度值对权值w和数据中心c进行调节，直到E满足精度要求，建立RBF神经网络软测量模型。

3 主导因素选择

影响SCR系统入口NOx质量浓度测量值的原始变量数较多，若直接采用原始变量进行RBF神经网络建模，会降低模型测量精度，增加网络模型的运算复杂度。因此，本文采用PCA和T2统计量监测，利用PCA和T2统计量对原始变量进行降维处理，从中选出与入口NOx质量浓度相关系数大的主导因素。其次，由于锅炉燃烧系统具有大滞后、强时延的特点，从炉膛燃烧工况变化到SCR系统入口NOx质量浓度改变往往需要较长的反应时间，而且CEMS浓度测量存在滞后时间，因此需要采用时间尺度分析法对初选因素与SCR系统入口NOx质量浓度的时间关系进行分析。最后，将筛选、分析和处理后的数据样本作为RBF神经网络的训练数据，建模流程如图1所示。

图1 建模流程Fig.1 Modelling flowchart

燃煤机组各台磨煤机启停的次序不同，因此在选择数据样本时，需要涵盖各个负荷段下的数据。根据表1所选原始变量，采集一段时间内机组日常运行数据(采样周期30 s)，数据包含高、中、低3个负荷段，同时剔除异常数据(如CEMS仪表吹扫、启停机等特殊工况)，形成建模数据原始样本。

3.1 影响因子分析

对采集的数据样本集进行PCA及T2统计量监测，由于所配煤种不同，各台磨煤机对SCR系统入口NOx质量浓度影响也不同，但对入口NOx质量浓度影响的时间尺度是一致的。根据分析绘制出主元特征值及其累计贡献率，如图2、图3所示。

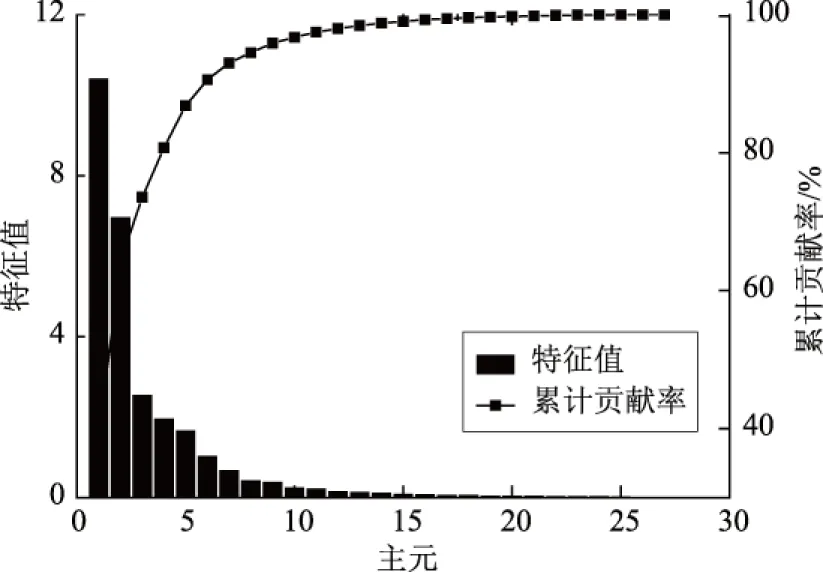
图2 主元特征值及其累计贡献率Fig.2 Principal component eigenvalue and cumulative contribution rate

图3 NOx质量浓度与T2统计量的变化曲线Fig.3 Variation curves of NOx mass concentration and T2 statistic

由图2可知，数据样本的变化趋势可以由前几个主元解释，第1、第2、第3、第4主元贡献量之和占比约81.2%，可以作为软测量模型输入参数。由图3可知，当T2统计量达到最大时，对应的入口NOx质量浓度也随之出现较大的波动，可见T2统计量与SCR系统入口NOx质量浓度是有关联的。

各原始变量对第1、第2、第3、第4主元的贡献量如图4至图7所示。

在T2统计量最大值时，由图4至图7可知，A磨瞬时煤量、A磨一次风压对主元贡献最大，其次D磨瞬时煤量、D磨一次风压、E磨瞬时煤量、E磨一次风压、F磨瞬时煤量、F磨一次风压、烟气含氧量、总煤量等对主元贡献较大。由于各台磨的煤量与风量具有较强的关联性，因此可以选择其一作为软测量参数，选取变量见表2。

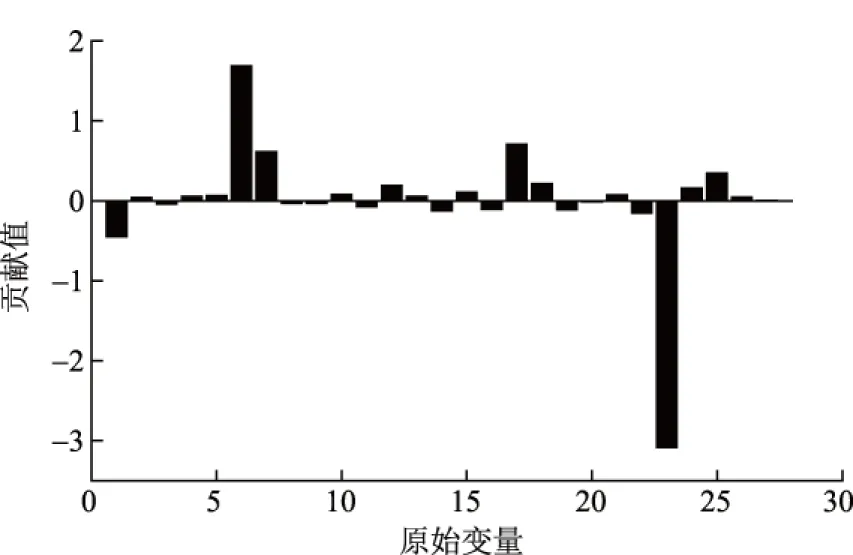
图4 各原始变量对第1主元的贡献量Fig.4 Contribution of original variables for the first principal component

图5 各原始变量对第2主元的贡献量Fig.5 Contribution of original variables for the second principal component

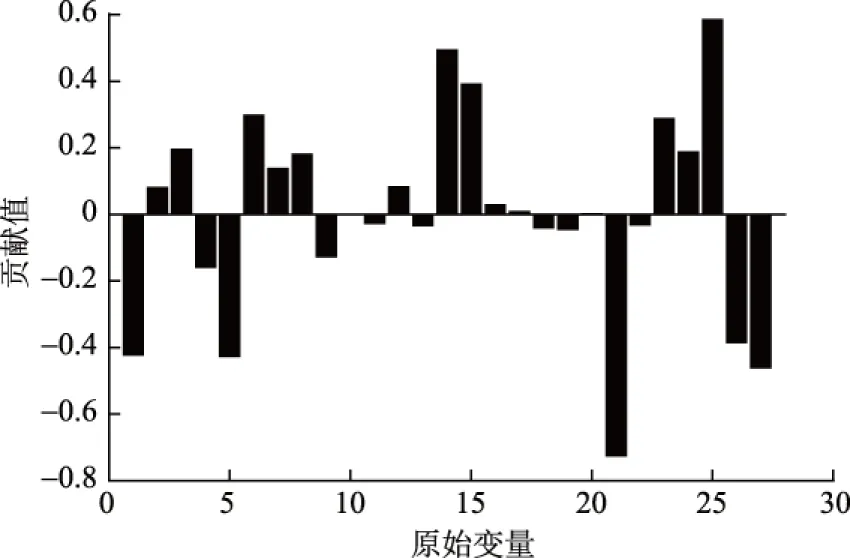
图6 各原始变量对第3主元的贡献量Fig.6 Contribution of original variables for the third principal component

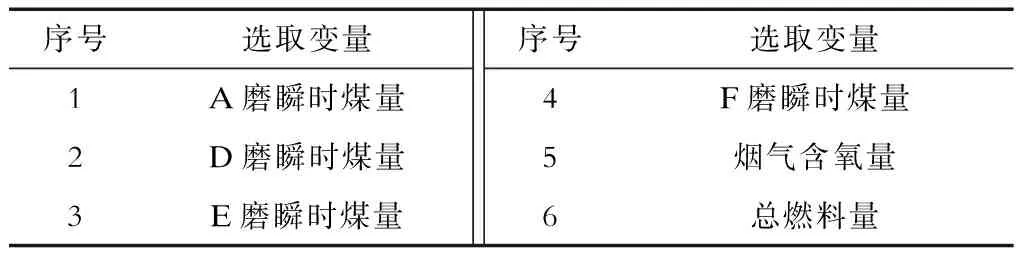
表2 初选变量Tab.2 Primary selected variables

图7 各原始变量对第4主元的贡献量Fig.7 Contribution of original variables for the forth principal component

3.2 入口NOx质量浓度时间尺度分析

表2中初选变量与SCR系统入口NOx质量浓度存在时间尺度，需要进一步对筛选后的变量进行分析。采集一段40%PN～60%PN(PN为额定负荷)负荷段下数据，时间间隔为30 s。按照式(6)的计算方法，逐个分析初选变量与SCR系统入口NOx质量浓度的时间尺度，结果如图8、图9所示。F磨瞬时煤量与入口NOx质量浓度在510 s时相关性最大，即S达到最小值，反映了当F磨瞬时煤量变化后，经过煤粉输送、炉膛燃烧等惯性环节，入口NOx质量浓度发生变化，时间过程约为510 s。同理，当炉膛烟气含氧量发生变化后，约30 s后入口NOx质量浓度发生变化。

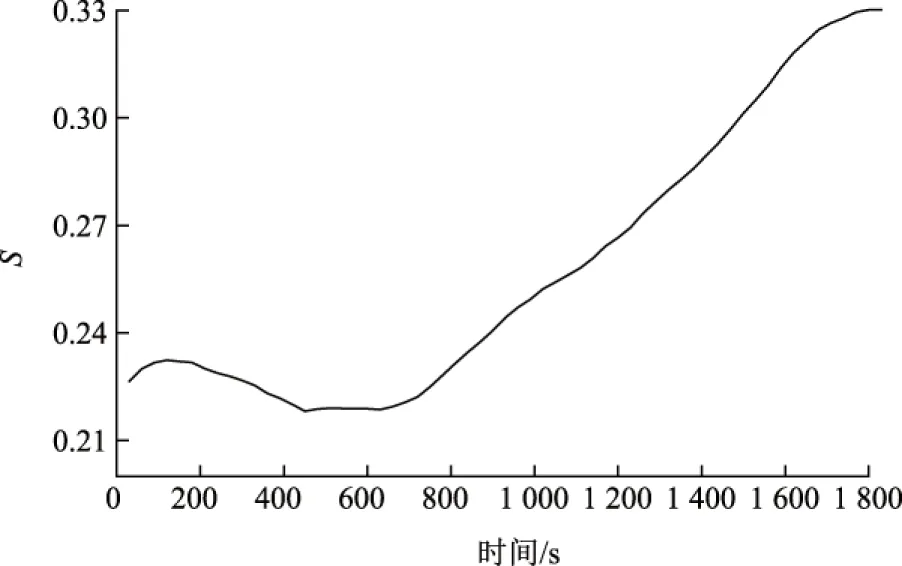
图8 F磨瞬时煤量与SCR系统入口NOx质量浓度的相关性指标曲线Fig.8 Curve of correlation between F instantaneous coal consumption and NOx mass concentration at SCR system inlet

由于各台磨煤机瞬时煤量与总煤量属于同一性质参数，它们与入口NOx质量浓度的时间尺度可以视为一致，经过分析后得出：各台磨煤机瞬时煤量、烟气含氧量与入口NOx质量浓度时间尺度分别为510 s、30 s。软测量数据集中的各个初选变量是同时刻采集的，因此需要对数据集各变量进行时间尺度移位后，构建出新的相关程度更高的数据样本集，作为RBF模型的输入。

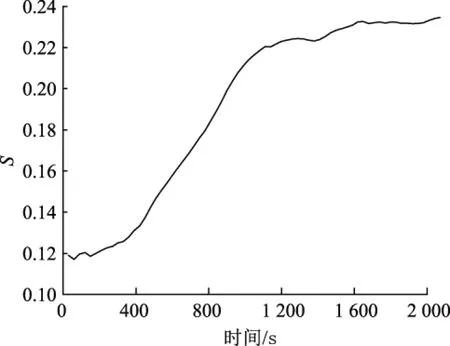
图9 烟气含氧量与SCR系统入口NOx质量浓度的相关性指标曲线Fig.9 Curve of correlation between oxygen content in flue gas and NOx mass concentration at SCR system inlet

3.3 软测量模型

采用3层网络结构的RBF作为入口NOx质量浓度软测量模型，将初选变量进行相应的时间尺度移位后作为软测量模型的输入，SCR系统入口NOx质量浓度则作为模型的输出。由于软测量各个变量的数据量纲不同，直接进行网络训练将会增加权值系数训练难度，降低模型训练精度。因此，需要将其标准化处理后统一量纲，以便于软测量参数的辨识和学习。

4 入口NOx质量浓度软测量仿真建模

带时间尺度PCA-RBF神经网络采用6-20-1的网络结构，采集机组日常运行数据，经过数据筛选处理后，作为RBF神经网络软测量训练样本，采样周期为30 s，样本总数为1 810。训练次数设为20 000，目标误差设为0.1%，隐含层数据中心学习系数为0.000 1，隐含层扩展常数学习系数为0.000 1，隐含层输出权值学习系数为0.000 01。

为了验证带时间尺度PCA-RBF模型的软测量效果，对比RBF、PCA-RBF、带时间尺度PCA-RBF这3种模型，训练误差曲线如图10所示，训练结果如图11所示，3种模型训练误差对比见表3。

可以看出，3种模型的训练结果与目标曲线基本拟合，当模型均为6-20-1的网络结构时，带时间尺度PCA-RBF模型训练均方差小于PCA-RBF

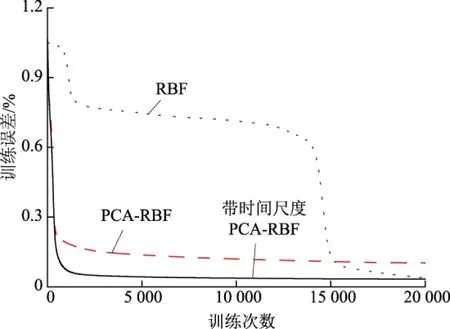
图10 网络训练误差曲线Fig.10 Net training error curves

图11 训练值与目标值对比Fig.11 Contrast of training and target values

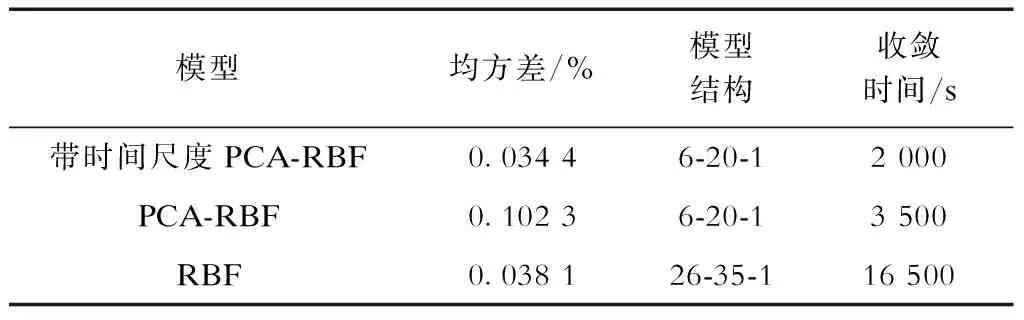
表3 3种模型训练误差对比Tab.3 Contrast of training errors of three models

模型，且带时间尺度PCA-RBF模型的收敛时间也早于PCA-RBF模型；RBF模型与带时间尺度PCA-RBF模型训练均方差相差不大，但RBF模型结构更复杂，参数更多，且收敛时间远远大于带时间尺度PCA-RBF模型。因此，通过对比分析可以看出，带时间尺度的PCA能够有效简化软测量模型结构，加快模型收敛速度，减小模型训练误差。

为了检验带时间尺度PCA-RBF模型的泛化能力，将训练好的模型和分析后的时间尺度应用于实际入口NOx质量浓度预测，选取该机组变负荷工况下的运行数据。因CEMS仪器吹扫的原因，采集的样本数据需要剔除吹扫时刻的NOx质量浓度值后作为预测数据样本，样本总数为579，采样周期为1 s。RBF、PCA-RBF、带时间尺度PCA-RBF这3种模型的预测效果如图12所示，3种模型的预测误差对比见表4。带时间尺度PCA-RBF模型与预测目标值基本拟合，预测误差为0.050 6%，而PCA-RBF和RBF模型输出均出现了较大偏差，存在过拟合现象。

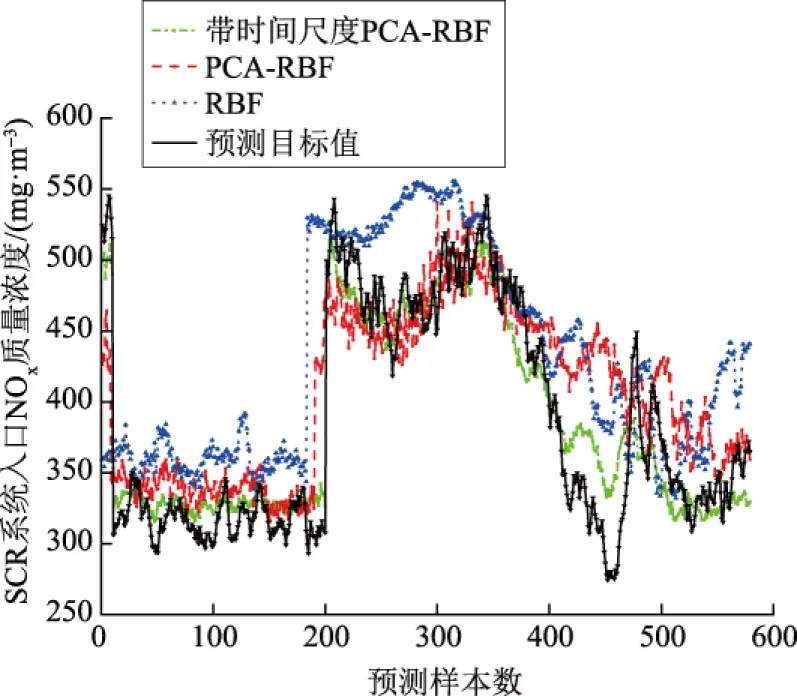
图12 预测值与目标值对比Fig.12 Contrast of prediction and target values

表4 3种模型预测误差对比Tab.4 Contrast of predictive errors of three models

5 结束语

本文通过数据分析为RBF神经网络筛选出适合建模的数据样本，先后通过脱硝系统影响因素分析、PCA及T2统计量监测，从SCR系统入口NOx质量浓度的影响变量中选出6个初选变量作为RBF神经网络模型输入，再通过时间尺度分析获得各个初选变量与SCR系统入口NOx质量浓度的时间关系，构建相关程度高的训练样本集，有效降低RBF神经网络模型结构，提高模型收敛速度。本文提出的带时间尺度PCA-RBF模型能够克服传统CEMS仪表时延、仪表吹扫造成测量不准的难题，有效提升燃煤机组脱硝系统的NOx浓度自动控制效果。