基于波形统计分析的频率振荡相关联机组快速识别技术

朱余启, 陈汝昌，戈本星，沈力

(1. 云南电网有限责任公司云南电力调度控制中心, 云南 昆明 650041；2. 南京南瑞继保电气有限公司，江苏 南京 211102)

云南电网与南方主网异步运行之后[1]，由于云南电网水电装机容量大且占比高[2]、省内负荷水平低、直流外送比例高的运行特征，网内先后出现数次频率振荡情况[3]。当存在一次调频设置不合理[4-5]、二次调频参数设置不合理[6]、切机切负荷产生错误动作[7]、直流频率限制器动作[8]等情况时，均有可能发生频率振荡。

电力系统振荡的诊断与紧急控制的核心问题是振荡源识别，目前有2种主流方法：一是基于离线数据进行仿真与分析；二是基于相量测量装置(phasor measurement unit，PMU)毫秒级实测数据进行实时数据处理与分析。前者对模型参数的准确性要求较高，且对设备异常、模型与参数变化所引起的振荡往往无能为力[9]。后者需要基于广域测量系统实时数据进行大量的处理与分析，通过分析各种电气量(包括电压、电流、出力、功角等)来诊断振荡。本文只讨论后者实时分析方法，并基于此提出解决方案，即采用秒级数据进行波形统计分析的方法。文献[10]使用振荡特征迭代函数的方法证明了秒级曲线也可以用作识别电网频率振荡。

实时分析方法所采取的方案有电气量的暂态分量判别法和稳态分量判别法，大部分文献采用的是暂态分量判别法。文献[11]利用电压行波暂态量分析定位振荡源头；在电力系统发生机电振荡时，发电机转子的动能、势能与网络中的势能不断转化，文献[12]利用发电机转子的动能、势能与网络中势能的暂态量分析定位振荡源头；文献[13]利用振荡时各个机组的转子相位、电压相位的不同分布情况判别振荡源头；文献[14]根据失步中心同侧和异侧的站点电压频率传播方向不同，在大区域互联电网判断失步振荡中心。利用暂态分量进行频率振荡判别的方法，优点是物理模型准确，能够从理论的角度确定分析振荡源头，缺点是对PMU数据的可靠性依赖较高，算法复杂，难以工程化。

利用电气量的稳态分量判别系统振荡的应用情况较少。文献[15]提出了使用发电机组功率谱密度来判别振荡的方案，但该方案局限于定位发电机机械功率扰动源。使用稳态分量判别法的优点是算法简单，易工程化应用，缺点是物理意义不清晰，目前仅在高压线路的振荡源头定位有明确的物理含义及原理推导，对于其他频率振荡情况并不能从理论上分析定位振荡源头。

本文并不需要严格对振荡源头进行定位，而只需要判断出频率振荡并识别影响频率振荡的关联机组，因此采用稳态分量判别方法。同时，通过分析波形数获取波形特征进行振荡机组判别的研究较少。文献[16]通过波形相关性分析了汽轮机阀门开度与机组功率振荡的关系；文献[17]通过分析电压波形与衰减正弦波的相关性判断是否发生低频振荡；文献[18]通过对低频含噪等幅振荡信号波形进行自相关功率谱分析来判别是否振荡。所以，本文提出通过分析频率和有功功率的稳态振荡波形来检测频率振荡，并判别相关联的振荡机组。该方法计算量小，结果直观，易于工程化实现。

文献[19]通过云南异步联网扰动实验实际数据说明，水电机组由于负阻尼效应而助增了频率振荡，火电机组由于正阻尼抑制了频率振荡，并且通过波形可以看出助增振荡的有功功率稳态波形基本与频率稳态波形同相位，而抑制频率振荡的有功功率稳态波形基本与频率反相位；同时通过BPA对水锤效应的水电机组调速器进行建模，成功复现了水电机组因为负阻尼助增频率扰动的现象，仿真出的波形与实际实验的波形近似。据此原理，本文的频率振荡判别与振荡机组快速识别技术的分析步骤如下：首先使用Prony算法对频率波形进行分析，判断是否发生振荡[20-21]，对出力波形计算标准差，当标准差满足一定大小时才认为其影响频率振荡；然后将频率和出力2个不同量纲的数据标准化为均值为0、方差为1的数据；计算频率与出力的皮尔森系数，当皮尔森系数绝对值满足一定大小时才认为其与频率振荡相关联，并且通过皮尔森系数的正负号确定该出力是助增还是抑制频率振荡；最后以标准差和皮尔森系数之积作为综合相关系数，对关联振荡机组助增或抑制频率振荡的能力进行排序。

1 频率振荡辨识

Prony算法是电力系统中普遍使用的辨识电网低频振荡的方法，本文采用Prony算法对频率振荡进行识别。同时，使用调度主站系统采集的电网频率秒级数据，以便实现快速采集、快速计算、快速分析。

1.1 Prony算法原理

Prony算法用一组衰减正弦函数的线性组合来拟和等间距采样数据，从中分析出信号的幅值、频率、相位、阻尼因子等信息。

y=∑Ae-λtcos (2πft+θ).

(1)

式中：y为待分析的信号；t为时间；A为信号幅值；λ为衰减因子；f为频率；θ为相位。

当输入一串等距离散序列x(0)，x(1)，…，x(N-1)，N为离散序列的点数，需要用P阶的衰减正弦函数来表达这一串序列，即

(2)

式中：bi=Aejθi,zi=eλi+j2πfi。即已知x(0)，x(1)，…，x(N-1)，求解bi与zi。

Prony算法的求解流程如下：

a)构造二阶样本矩阵。定义二阶样本矩阵函数

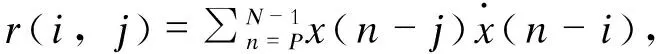
i,j=0，1，…，P.

(3)

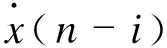
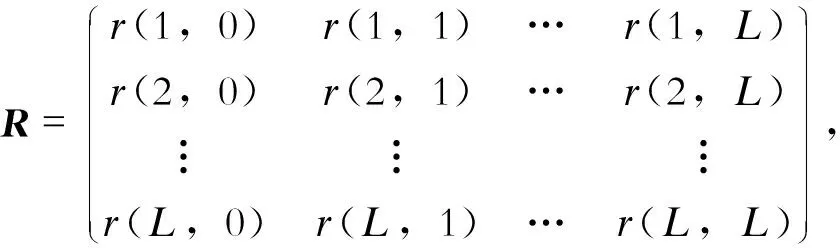
(4)

为了使样本矩阵全面反映系统信息，维数L取其最大值N/2。

b)确定计算阶数。在计算前需要通过一定的规则确定模型阶数P，一般采用奇异值分解(singular value decomposition，SVD)算法。SVD算法的实质是求解一个最优化问题，利用Frobineous范数定阶方法确定样本矩阵的有效秩序P。

c)求解回归参数。求解式(5)的回归参数a1，a2，…，aP，其中εP为自定义的最小误差能量：

(5)

d)求解特征方程。特征方程的形式为1+a1z-1+…+aPz-P=0，求解得到特征根zi(i=1，2，…，P)，即前文的zi=e(λi+j2πfi)，也称为Prony极点。

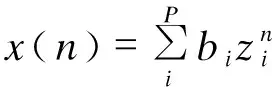
(6)

得到整个采样区间的表达式

最终利用bi=Aejθi,zi=eλi+j2πfi，求解θi、fi。

1.2 基于Prony算法的频率振荡辨识方法

综合异步联网的云南电网多年运行情况，给定的频率振荡定值设置如下：频率振荡幅值定值为0.1 Hz，当振荡分量幅值大于0.1 Hz时认为发生了振荡；衰减因子绝对值定值为0.1，衰减因子绝对值过大说明振荡衰减迅速，不纳入考虑；当振荡分量的幅值大于0.1 Hz并且衰减因子绝对值小于0.1时，判定该振荡分量有效。

2 关联振荡机组识别及排序方法

2.1 计算出力标准差

在进行数据标准化之前，首先计算出力曲线的标准差，以判断出力波动的程度。当标准差过小时认为对振荡没有影响，当标准差满足一定条件时才认为能够影响频率振荡。后续将采用标准差与皮尔森系数之积作为综合相关系数，作为排序的标准。

2.2 数据标准化

进行相关性分析之前，需要对电网频率数据与机组出力数据进行预处理，将不同量纲的频率和出力数据标准化为均值为0、方差为1的数据。

(7)

式中：Xi为第i个原始数据，z(Xi)为其标准化后的值；μ为均值；σ为标准差。

2.3 计算频率与出力皮尔森系数

2.3.1 皮尔森系数

皮尔森相关系数

(8)

式中：cov(X,Y)为向量X与Y的协方差；σX为向量X的标准差；σY为向量Y的标准差。皮尔森相关系数(Pearson correlation coefficient)也称皮尔森积矩相关系数(Pearson product-moment correlation coefficient)，是一种线性相关系数。皮尔森相关系数是用来反映2个变量线性相关程度的统计量。rc描述的是2个变量间线性相关强弱的程度，rc的绝对值越大表明相关性越强。

简单的相关系数的分类：rc值为0.8～1.0表示极强相关；rc值为0.6～0.8表示强相关；rc值为0.4～0.6表示中等程度相关；rc值为0.2～0.4表示弱相关；rc值为0.0～0.2表示极弱相关或无相关。

rc的取值在-1与+1之间：若rc>0，表明2个变量是正相关，即一个变量的值越大，另一个变量的值也会越大；若rc<0，表明2个变量是负相关，即一个变量的值越大，另一个变量的值反而会越小。

2.3.2 仿真计算结果

虽然皮尔森系数rc描述的是2个变量间线性相关强弱的程度，但当变量为正弦波时，亦可用皮尔森系数描述相关性。仿真结果如图1、图2、图3所示，其中幅值为归一化数值。

图1 幅值不同的正弦波相关系数Fig.1 Correlation coefficients of two sine waves with different amplitudes

图2 频率不同的正弦波相关系数Fig.2 Correlation coefficients of two sine waves with different frequency

图3 相位不同的正弦波相关系数Fig.3 Correlation coefficients of two sine waves with different phases

图2中，2个正弦波频率分别为1/2π和1.5/2π时，皮尔森系数计算结果为-0.243 5，即弱负相关。

图3中：2个正弦波相位差为π/3时，皮尔森系数计算结果为0.505 4，即正相关；2个正弦波相位差为2π/3时，皮尔森系数计算结果为-0.433 9，即负相关。

通过比较频率波形与机组出力波形的相关系数可以判断出频率波形与机组出力波形的相位差，从而判断出机组出力是助增频率振荡还是抑制频率振荡，以及助增频率振荡或是抑制频率振荡关联性的大小，从而对关联机组进行排序，提供给调度员分析决策。

2.4 关联振荡机组排序

本文采用皮尔森系数与标准差之积作为综合相关系数，以综合相关系数的大小对机组出力进行排序。根据运行经验，需要对皮尔森系数和标准差设立计算门槛。皮尔森系数绝对值必须大于0.4，即出力与频率的相关性必须满足一定要求；标准差必须大于2 MW，即认为出力波动到一定情况才认为对电网有影响。满足这两者定值才参与排序，否则认为和频率振荡无关。

当皮尔森系数和标准差满足门槛时：综合相关系数大于0，认为助增频率振荡；综合相关系数小于0，认为抑制频率振荡；综合相关系数绝对值越大，影响频率振荡越强；综合相关系数绝对值越小，助增频率振荡越弱。

3 实际算例分析

3.1 频率振荡辨识结果

对2020年7月某日发生的频率振荡数据进行分析，选取5 min(即样本点数为300)的振荡数据，频率数据如图4所示。对实际频率进行Prony分析，结果见表1。

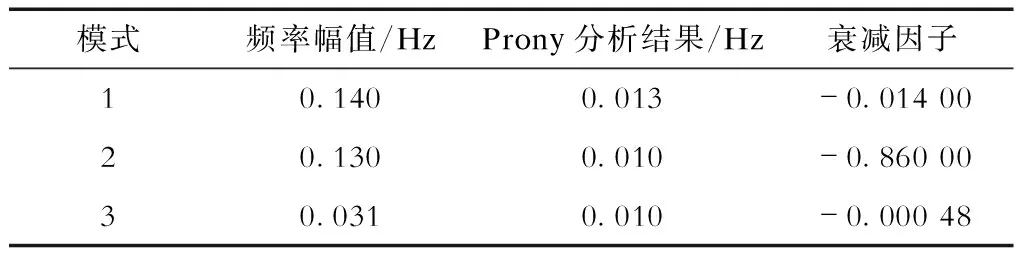
表1 频率Prony分析Tab.1 Prony analysis of frequency

根据振荡幅值定值0.1以及衰减因子绝对值定值0.1，即振荡分量的幅值大于0.1并且衰减因子绝对值小于0.1时判定该振荡分量有效。这里认为模式1的振荡分量有效，即认为发生了频率振荡。

3.2 关联振荡机组识别结果

分别以糯扎渡电厂、小湾电厂、普西桥电厂、滇东电厂为例进行分析。

糯扎渡电厂出力与频率曲线如图5所示，计算结果为：皮尔森系数0.69、标准差15.43、综合相关系数10.65。从皮尔森系数可以看出糯扎渡电厂出力助增了频率振荡，从出力标准差看出电厂发生了一定程度的振荡，所以认为综合相关系数有效，该电厂为关联振荡的电厂，并且助增频率振荡。

小湾电厂出力与频率曲线如图6所示，计算结果为：皮尔森系数0.12、标准差49.94、综合相关系数6.17。从皮尔森系数可以看出小湾电厂出力与频率振荡无关，从出力标准差看出电厂出力变化较大，所以认为综合相关系数无效，该电厂与振荡无关。

普西桥电厂出力与频率曲线如图7所示，计算结果为：皮尔森系数0.50、标准差4.00、综合相关系数2.00。从皮尔森系数可以看出普西桥电厂出力助增了频率振荡，从出力标准差看出电厂发生了一定程度的振荡，所以认为综合相关系数有效，该电厂为关联振荡的电厂，并且助增频率振荡。

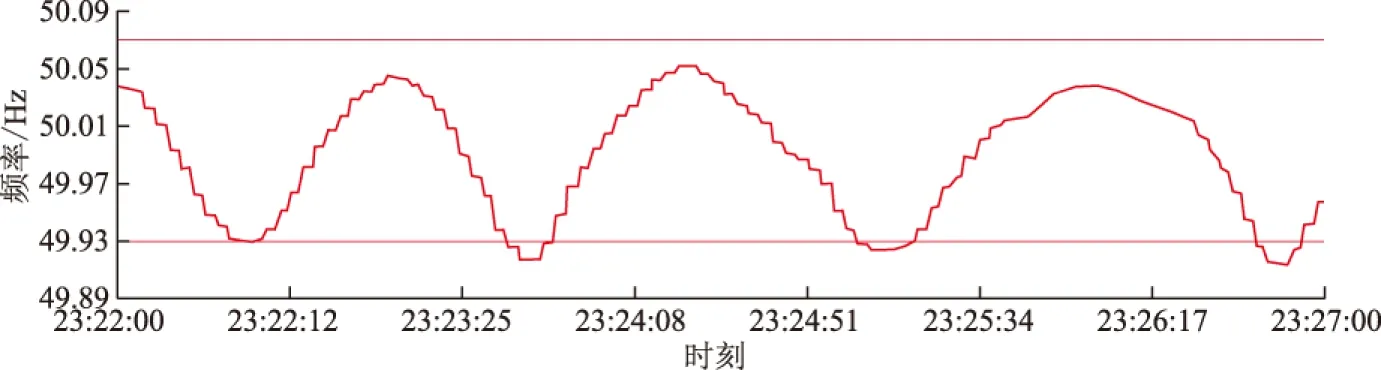
图4 频率曲线Fig.4 Frequency curve

图5 糯扎渡电厂出力与频率曲线Fig.5 Output and frequency curves of Nuozhadu power plant

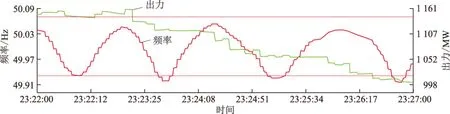
图6 小湾电厂出力与频率曲线Fig.6 Output and frequency curves of Xiaowan power plant

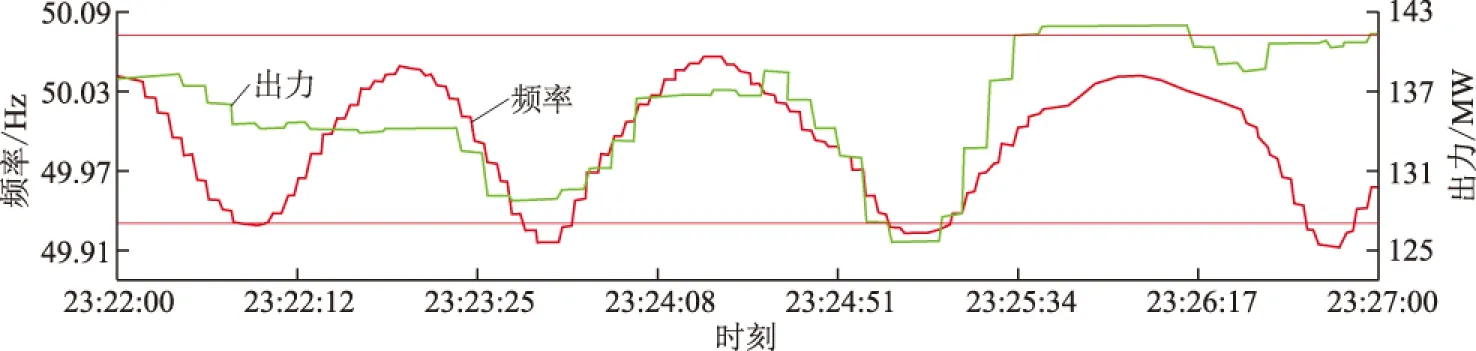
图7 普西桥电厂出力与频率曲线Fig.7 Output and frequency curves of Puxiqiao power plant

滇东电厂出力与频率曲线如图8所示。计算结果如下：皮尔森系数-0.85、标准差3.85、综合相关系数-3.27。从皮尔森系数可以看出滇东电厂出力抑制频率振荡，从出力标准差看出电厂出力变化较大，所以认为综合相关系数有效，该电厂为关联振荡的电厂，并且抑制频率振荡。

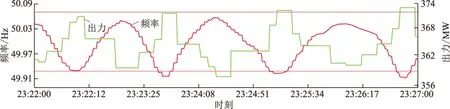
图8 滇东电厂出力与频率曲线Fig.8 Output and frequency curves of Diandong power plant

4 结束语

云南电网与南方电网主网异步运行之后，云南电网频率稳定问题逐渐突出。当电网频率发生振荡时，需要监控系统能快速响应，在判别频率振荡的同时快速定位振荡源头。本文提出：首先，使用Prony算法对频率秒级曲线进行分析，判断频率是否发生振荡；其次，对出力波形计算标准差，当标准差满足一定大小才认为其影响频率振荡；然后，对出力数据进行标准化，将频率和出力2个不同量纲的数据标准化为均值为0、方差为1的数据；接着，计算频率与出力的皮尔森系数，当皮尔森系数绝对值满足一定大小才认为其和频率振荡相关联，并且通过皮尔森系数的正负确定该有功出力是助增还是抑制频率振荡；最后，以标准差和皮尔森系数之积作为综合相关系数，对关联振荡机组助增或抑制频率振荡的能力进行排序。实际算例分析结果表明，本文提出的算法能够正确识别系统频率振荡，并且能够快速定位关联振荡机组。