锂离子电池异构建模及内部传质机理探究:粒径分布的影响
2021-03-06陈怡沁许于周静红隋志军周兴贵
陈怡沁,许于,周静红,隋志军,周兴贵
(华东理工大学化学工程联合国家重点实验室,上海200237)
引 言
锂离子电池作为一种新型储能设备,自20世纪90 年代初实现商用化后,在能源存储和新能源汽车领域发挥着重要作用[1]。通过对其电极活性材料的持续研究开发[2],锂离子电池技术在近年来获得了快速发展,其应用领域也不断拓宽,同时也对锂离子电池的管理和设计提出了更高的要求。由此,产生了可预测电池工程应用性能的等效电路模型和可指导电池优化设计的电化学模型[3−4]。其中,由Newman 等[5−6]提出的准二维模型(Newman 模型)是目前最具前景的电化学模型,它将锂离子电池内部电化学反应动力学、传质、传热等微观反应过程数值化,从电化学机理层面描述了锂离子电池充放电行为,可用来模拟计算电极厚度、孔隙率[7−8]等工艺参数对电池性能的影响机理,指导电池的优化设计。
本课题组前期的研究中[9]也采用Newman 模型探究了LiFePO4(LFP)材料颗粒纳米化对提升锂离子电池倍率性能的影响机制,定量分析了均一的不同粒径LFP颗粒对于锂离子电池性能的影响。但由于Newman 模型采用多孔均质电极材料的假设,所以无法直接利用该模型研究非均相结构的电极,即活性材料颗粒存在粒径分布的电极。而实际电极难以做到均质多孔结构,活性材料颗粒往往存在着较宽的粒径分布,大量实验研究[10−13]也证明了粒径的分布对锂离子电池的电化学性能有不可忽略的影响。例如Hong 等[12]通过控制锂的用量调节了LFP/C 复合材料的粒度分布,发现减少一次粒子的团聚能够提升电池性能。但是实验研究一方面难以实现粒径分布的精确控制,另一方面也只能根据实验测得的总体电化学性能与不同的电极材料粒径分布做表观的定性关联,无法分析不同粒径大小的电极材料颗粒在充放电过程中的行为和作用。为了研究电极材料颗粒的粒径分布对其电化学性能的影响,有研究者对Newman 模型做了拓展,用以模拟非均相电极的电化学性能。例如,Röder等[14]将粒子大小作为一个分布参数引入到Newman 模型中,研究了石墨电极的颗粒尺寸分布对性能的影响,结果表明颗粒尺寸分布及其变化对锂离子电池的性能劣化有很大的影响。这种拓展的Newman 模型虽然能定量研究粒径分布对锂离子电池性能的影响,但无法描述不同粒径颗粒的影响机制。
异构模型是一种采用几何结构描述模拟对象结构信息的建模方法,将其应用在锂离子电池模拟中,可以直接反映多孔电极颗粒实际形状。已有一些研究者[15−17]开发了三维电极微观结构的模型,例如Awarke等[17]采用三维异构模型研究了LFP电极内部应力对孔隙率和导电性的影响。
借助异构模型建立非均相电极的几何结构,再结合Newman 模型,模拟研究电极活性材料颗粒存在粒径分布时的充放电行为,以阐明存在粒径分布的电极中不同大小颗粒在充放电过程中的作用机制,迄今未见该方面的研究报道。本文采用二维异构模型,针对LFP锂离子电池的正极,首先建立单一粒径几何结构,结合Newman 模型模拟锂离子电池的恒流放电过程,分析了粒径的改变对电极内部传质的影响;其次建立双粒径几何结构,结合Newman模型模拟粒径分布对电池性能的影响,定量探究了不同粒径颗粒内的传质情况和粒径分布对电池性能的影响机制。
1 建模与计算
1.1 模型描述与假设
锂离子电池常以碳素材料为负极,以含锂的化合物为正极,其充放电过程就是锂离子的嵌入和脱嵌过程。本文以常用的石墨−LFP 体系组成的锂离子电池作为研究体系,负极和隔膜区采用准二维模型(Newman 模型)、正极区采用二维异构模型结合Newman 模型来描述电池内部的传质与电化学过程。
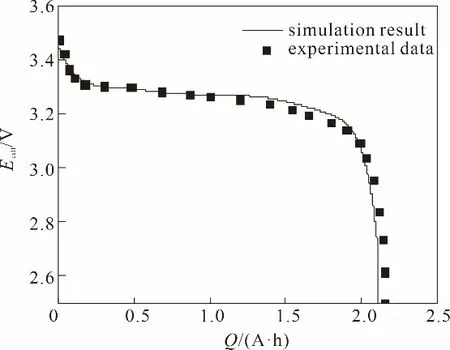
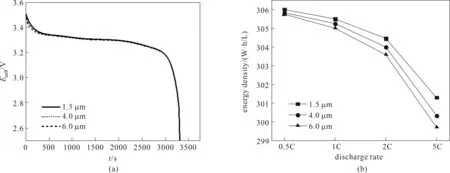
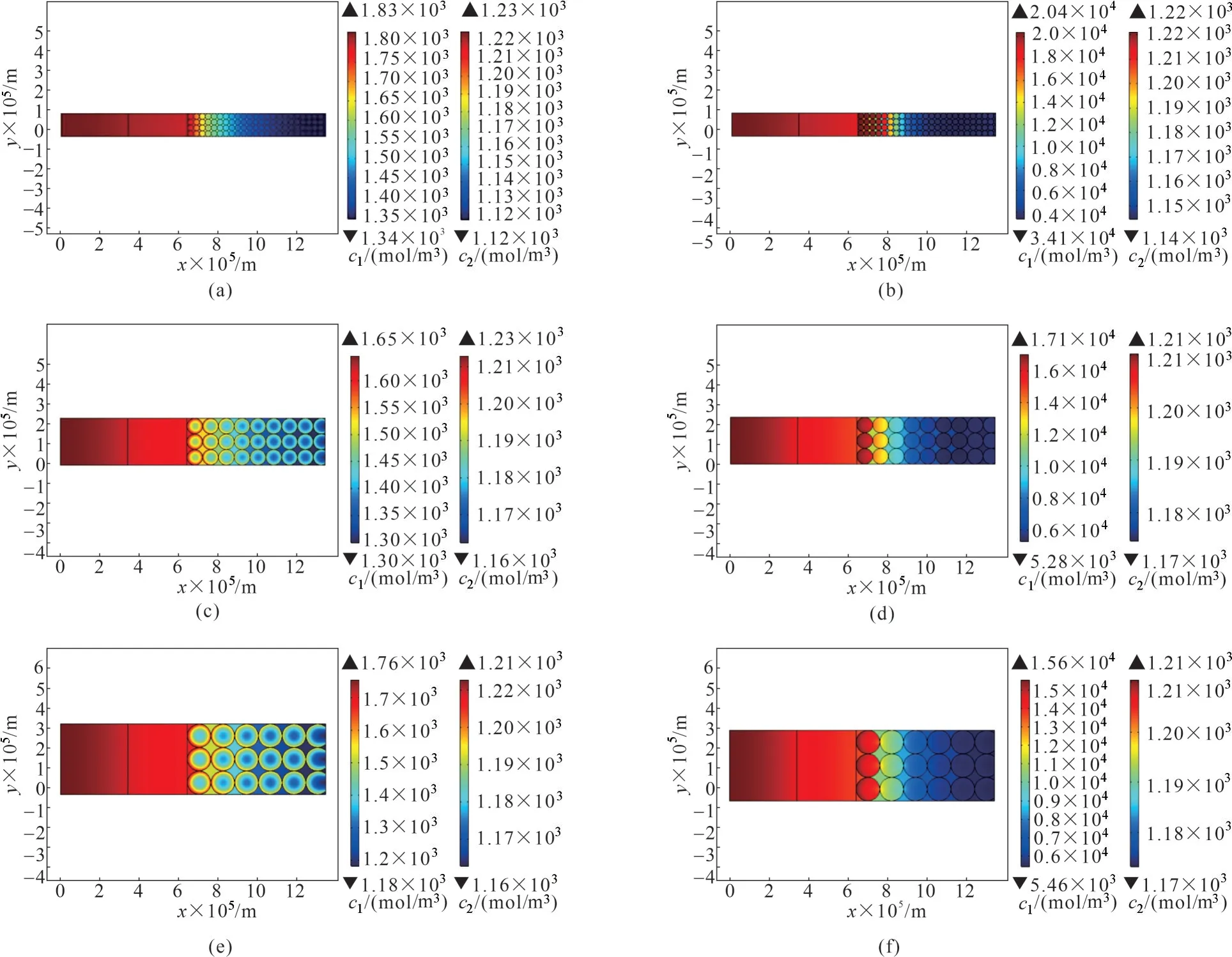
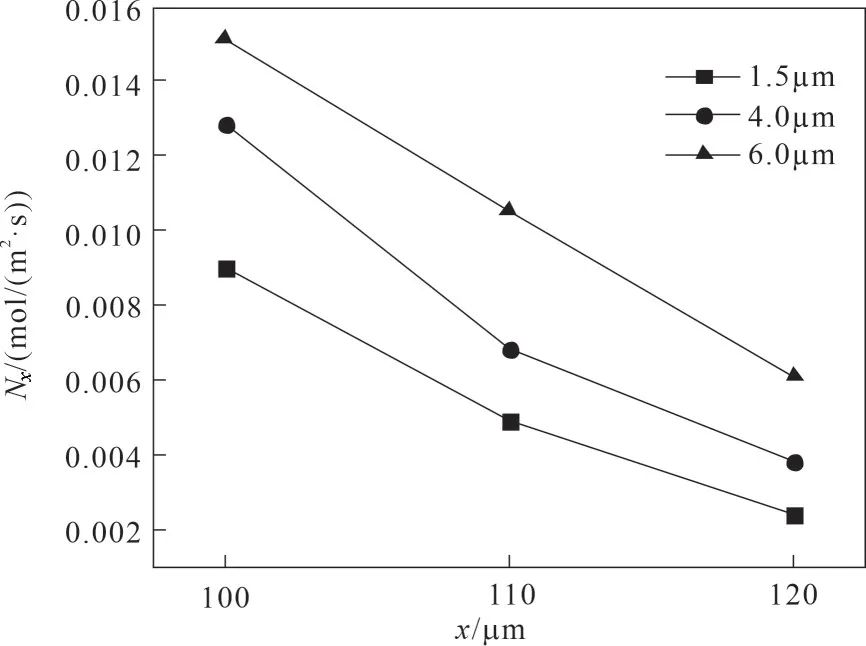
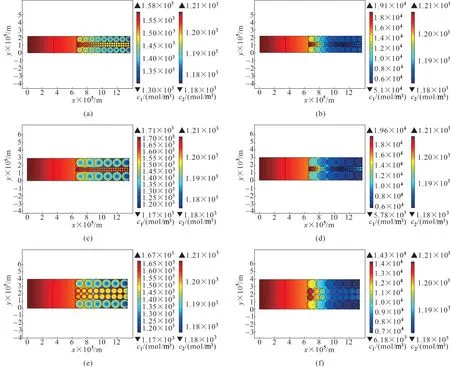
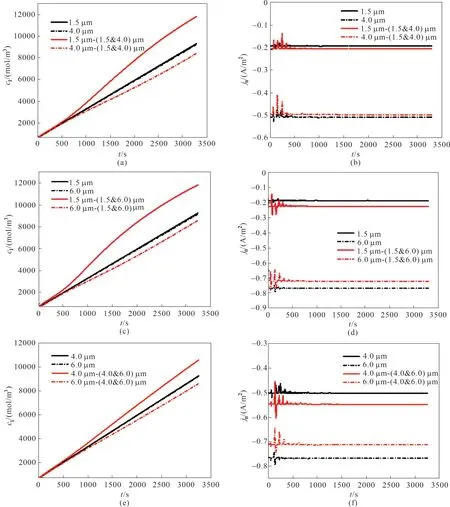
图1 为锂离子电池异构模型的几何结构,其中对负极区域(0 图1 单粒径锂离子电池几何结构示意图(a);双粒径锂离子电池几何结构示意图(b)Fig.1 Geometry schematic of lithium ion battery with positive electrode of single−sized particles(a);Geometry schematic of lithium ion battery with positive electrode of bimodel−sized particles(b) 同时为了简化计算过程,本文进行了如下假设: (1)忽略锂离子电池运行中产生的气体,只考虑电池中液相和固相的作用; (2)锂离子电池运行中的副反应可以被忽略; (3)在正极中的活性物质被认为是均匀的,并且是由球形颗粒组成,且不考虑黏结剂和导电剂; (4)忽略SEI 膜和集流体对锂离子电池性能的影响; (5)整个锂离子电池内部温度恒定; (6)忽略后期的压片工艺等对正极材料电化学性能的影响。 负极和隔膜区的控制方程参见文献[9]。 正极区域由于几何结构的不同,分为固体颗粒和液态电解质两个域。由于采用几何结构描述多孔电极,所以质量平衡方程中不涉及孔隙率这一参数。具体如下。 在固体颗粒域内,利用Fick 定律来描述电极材料颗粒内固态锂的扩散,如式(1)所示: 式中,c1为活性电极材料球形颗粒内锂的浓度;t为扩散时间;D1为固态锂在活性电极材料中的扩散系数。在活性电极材料颗粒表面的锂浓度与锂离子在电解质溶液中输运的浓度与通量进行耦合,在颗粒中心的通量为零。 在液态电解质域内,利用浓溶液理论描述正极区域电解质溶液中锂离子浓度(c2)的变化,该过程由液相中锂离子的扩散、迁移以及界面上的电化学反应所控制,正极和隔膜内电解液中锂离子浓度控制方程如式(2)所示: 式中,ν+为每摩尔电解质解离生成锂离子的量,jn为电极表面局部电流密度;式(2)中等号右侧第一项为扩散项,第二项为迁移项,第三项为反应项;D2为电解液中锂离子的扩散系数,其随温度和锂离子浓度的变化关系如式(3)所示: 本工作中模拟的锂离子电池体系与商业电池C26650 的组成相同,该商用电池的容量为2.3 A·h,其负极材料是石墨,正极活性材料为LFP,电解质为1 mol/L LiPF6溶解在由碳酸乙烯酯、碳酸丙烯酯、碳酸乙酯和碳酸二甲酯混合而成的溶剂中,负极集流体由铜箔制成,正极集流体由铝箔制成。根据文献中给出的常规方法生产的LFP 颗粒粒径的分布范围[18],选定3 个粒径,分别为1.5、4.0 和6.0 μm,作为单粒径异构模型的几何参数。对上述的单一粒径颗粒进行两两组合,得到三种双粒径组合的电极单元,分别是(1.5&4.0)、(1.5&6.0)和(4.0&6.0)μm。模拟所需要的其他相关参数同文献[9]。 图2 单粒径(a)和双粒径(b)锂离子电池网格划分示意图Fig.2 Schematic of model meshing for lithium−ion battery with single−sized particle (a)and bimodel−sized particles(b) 本文模型使用基于有限元算法的商业软件COMSOL 4.3 的锂离子电池模块和稀物质传递模块进行耦合求解,为了提高计算结果的准确性,对全局网格划分选择极细化,如图2所示,模拟所对应的放电电压窗口为2.5~4.0 V。 另外,根据放电曲线可以计算出锂离子电池的能量密度,具体表达式如式(4)所示: 式中,V表示电池的体积。 为了检验异构模型引入LFP锂离子电池正极的几何结构后,采用Newman 模型模拟锂离子电池充放电性能的合理性以及采用C26650 型LFP 锂离子电池参数作为本工作模拟计算的模型参数的适用性,首先采用单粒径异构模型模拟计算了1 C 下锂离子电池在室温时的放电曲线,如图3 中的曲线所示。从图中可见,模拟放电曲线与Tay 等[19]在相同条件下对C26650 型锂离子电池进行充放电实验记录的放电曲线(图3 中的实验点)吻合良好,表明采用异构模型结合Newman 模型来模拟LFP 锂离子电池可以较好地预测锂离子电池的电化学性能,所采用的模型参数对于本文的异构建模工作是适用的。 图3 商用电池的异构模型模拟放电曲线与实测放电曲线比较Fig.3 Comparison between the simulated and the experimental discharge curves for commercial lithium ion battery 图4 给出了采用异构模型建模后,模拟计算得到1.5、4.0 和6.0 μm 三种单粒径锂离子电池正极的放电曲线和体积能量密度。从中可以看到随着电极材料颗粒粒径的减小,锂离子电池的能量密度随之增加,电池的能量密度随着放电倍率的增加而下降;同时,小粒径锂离子电池的倍率性能优于大粒径锂离子电池的倍率性能。这一计算结果与大量的实验研究结果相符,例如郭孝东等[18]实验研究发现,LFP 材料的一次粒径越小,其放电容量越高;交流阻抗测试也发现一次粒径越小,电极的反应阻力越小,更容易发生电荷转移。同时也与本课题组[9]采用Newman 模型定量分析LFP 颗粒粒径对电池性能影响的结果颇为一致。模拟计算表明,固相扩散速率是锂离子电池放电过程的主要限制因素,颗粒粒径减小后,颗粒内的传输路径缩短,从而降低了传递阻力。但Newman 模型对锂离子电池的模拟采用均质假设,因此模拟结果无法描述其电极内部物质传递过程与电极内几何结构的关系。本工作采用异构建模描述电极内的几何结构,并结合Newman 模型,可以直观呈现锂离子在多孔电极内电解液中的扩散和固态锂在活性电极材料颗粒内的传递过程,计算结果如图5所示。 图4 单粒径锂离子电池放电曲线(a)和能量密度(b)Fig.4 Discharge curves(a)and energy densities(b)of lithium ion battery with single−sized particle 图5 单粒径锂离子电池的电解液内锂离子浓度与颗粒内固态锂浓度分布随时间的变化Fig.5 The concentration distribution of lithium ion in the electrolyte and metal lithium in active particles for lithium−ion battery with single−sized particles 图5 为1 C 放电条件下,正极材料颗粒粒径为1.5、4.0和6.0 μm 的锂离子电池,在放电初期和末期时,电解液内锂离子和颗粒内固态锂的浓度分布情况。根据前文在1 C 下的放电曲线,将电池输出电压开始趋于稳定的时间点(300 s)设为放电初期,将电压开始降低的时间点(3000 s)设为放电末期;在正极材料颗粒上显示的是固态锂的浓度(c1),在其他区域显示的是电解质中锂离子的浓度(c2)。 从图5 中可以直观地看到,对单个正极颗粒而言,在放电初期,其表面的固态锂浓度较高,在材料颗粒径向上存在明显的浓度梯度;至放电末期,正极材料颗粒中固态锂浓度在颗粒径向上相差很小,在平行集流体方向上趋于相同。比较不同粒径的颗粒内在放电初期的锂浓度,见图5(a)、(c)和(e),可进一步发现,粒径越小,单个颗粒中固态锂的浓度差越小;反之,颗粒粒径越大,单个颗粒内的固态锂的浓度差越显著,这说明粒径的减小有助于减小颗粒内固态锂的传递阻力。对整个正极而言,在放电的初期和末期,不同粒径的正极内部固态锂呈现出相似的浓度分布情况,即靠近隔膜一侧的颗粒,其表面固态锂的浓度总是高于靠近集流体一侧的颗粒。值得指出的是,在放电末期[图5(b)、(d)和(f)],靠近隔膜侧的嵌锂量随粒径的减小而增大,这与大量研究达成的共识是一致的[20−21];而靠近集流体侧的正极颗粒内,嵌锂量随粒径的减小而减小。即,随着粒径的减小,正极两端固态锂的浓度差增大。 图6 1 C放电条件下放电500 s时,单粒径锂离子电池正极内部锂离子通量Fig.6 The lithium ion flux inside the positive electrode with single−sized particles when discharging for 500 s under 1 C discharge rate 为了进一步探究小颗粒电极两端固态锂浓度差较大的原因,通过Nernst−Planck 方程计算了锂离子电池在1 C 放电倍率下处于稳态放电(放电时间500 s)时,电极中靠近集流体侧(x=100、110 和120 μm 处)的颗粒间电解液中的锂离子通量,结果如图6 所示。从图中可以看出,在相同放电倍率下,随着粒径的减小,锂离子通量减少。这是由于在厚度相等的正极内,LFP颗粒规整排布时,锂离子的传输距离相同,粒径的减小造成颗粒间孔道减小,使得锂离子在颗粒间电解液内扩散阻力增加,相同时间内传输至集流体侧的锂离子量少于大粒径颗粒组成的电极。所以,集流体侧的电解液中锂离子浓度随粒径的减小而减小,导致该处LFP 颗粒内的嵌锂量随之减小,最终与隔膜侧的LFP 颗粒内固态锂的浓度差增大。 为了定量考察电极活性材料颗粒的粒径分布对其电化学性能的影响,将1.5、4.0、6.0 μm 三种粒径的电极材料颗粒两两组合形成双粒径电极单元来模拟存在不同粒径分布的电极,通过异构模型建立简化的几何结构,其示意图如图1(b)所示,组成的三种双粒径电极分别表示为(1.5&4.0)、(1.5&6.0)和(4.0&6.0)μm。利用Newman 模型对其放电过程进行模拟计算,研究其放电过程中金属锂在活性电极材料颗粒上的扩散、锂离子在电解质中的传递,并与单粒径模型的模拟结果对比。 2.3.1 单粒径与双粒径锂离子电池模拟结果对比三种不同粒径分布的电极单元及其对应的单粒径电极单元的能量密度对比如图7 所示,从图7 中可以看到,双粒径电极的能量密度均大于对应的较大单粒径电极的能量密度,其中,由1.5 μm 与4.0 μm两种颗粒组成的锂离子电池能量密度最高,(4.0&6.0)μm 的电极能量密度其次,(1.5&6.0)μm 的电极能量密度最小;且高倍率下,三种电极的能量密度差异较低倍率时更显著。Sheu等[22]采用两种不同粒径分布(2~4 和5~10 μm)的LiCoO2电极作为阴极,实验结果证明粒径分布为2~4 μm 的LiCoO2具有更高的质量比容量,随着放电倍率的增大,两种电极的质量比容量的差异增大,与本文的模拟结果规律一致。图7(a)、(c)显示,当两种粒径较为接近的颗粒组成电极时,得到的双粒径电极能量密度可大于对应两种单粒径电极的能量密度;图7(b)显示,组成双粒径电极的两种颗粒的粒径差别较大时,其能量密度介于对应两种单粒径电极的能量密度之间。对比图7(a)、(c)可知,总体粒径越小,能量密度越大,这与2.2节单一粒径电极模拟得到的规律一致。 图7 单粒径与双粒径的锂离子电池的能量密度Fig.7 Comparison of the energy densities of lithium ion batteries with single−sized particles and bimodel−sized particles 施柳柳[23]选择了三种中位粒径(1.5、4 和7 μm)的LiFePO4材料进行两两级配,得到级配后的体积能量密度高于单一粒径材料,较小粒径1.5 μm 和4 μm 的材料颗粒进行级配拥有较好的电化学性能,1.5&7 μm 和4&7 μm 的电极能量密度接近,且远小于1.5&4 μm的电极,与本文得到的结论一致。 2.3.2 双粒径模拟结果分析 图8 为1 C 放电条件下,三种粒径两两组合的锂离子电池,在放电初期和末期时,电极中锂离子和固态锂的浓度分布情况。在正极材料球形颗粒上显示的是固态锂的浓度(c1),在其他区域显示的是电解质溶液中的锂离子的浓度(c2)。 从图8 中可以看到,与单粒径电极单元不同的是,在双粒径的电极单元中,由于电极材料颗粒粒径大小存在差异,导致固态锂在电极材料颗粒上的传递速度存在差异,无论在放电初期还是末期,垂直于集流体方向上,大颗粒上的固态锂浓度始终小于小颗粒上的固态锂浓度。这是因为小颗粒内部固态锂的传输距离短,阻力小,所以锂离子优先嵌入小颗粒中。Li等[24]结合扫描透射X 射线显微镜和PTY 显像与透射电子显微镜,通过测量部分放电电极中约800 个LFP 粒子的单粒子荷电状态,确定了LFP 电极的锂化顺序,结果发现小颗粒比大颗粒先锂化。这一实验结果表明本文模拟可以较好地描述实际充放电过程中不同粒径颗粒的作用。 为了更明确地比较两者固态锂的分布情况,根据图8 计算结果,表1 列出了不同粒径锂离子电池内的固态锂浓度以及浓度差。从中可以看出,在放电末期,双粒径锂离子电池的正极内部固态锂浓度差小于单粒径锂离子电池。为了证实粒径的分布对锂离子的传递有影响,通过Nernst−Planck 方程计算了双粒径锂离子电池在1 C 放电倍率下处于稳态放电(放电时间500 s)时,电极中靠近集流体侧(x=100 μm 处)的锂离子通量,并与单粒径锂离子电池对比,结果如图9 所示。从图9 中可以看出,当存在粒径分布时,正极内部电解液中锂离子通量增大,说明较大颗粒可以在较小颗粒附近引入大孔道,有效降低了锂离子在电极内部颗粒间的整体扩散阻力。 图8 双粒径锂离子电池电解质溶液中锂离子与颗粒内固态锂的浓度分布随时间的变化Fig.8 The concentration distribution of lithium ion in the electrolyte and metal lithium in active material particles for the lithium−ion battery with bimodel−sized particles 表1 1 C条件下放电3000 s时,单粒径和双粒径锂离子电池正极内部最大/最小固态锂浓度Table 1 The maximum and minimum concentration of the metal lithium in the positive electrode with single-sized particles and bimodel-sized particles when discharging for 500 s under 1 C discharge rate 图9 1 C 放电时,双粒径及单粒径锂离子电池正极中(x=100 μm),靠近集流体处的锂离子通量随时间的变化曲线Fig.9 The lithium ion flux during discharge time inside the positive electrode with single−sized particles and bimodel−sized particles(x=100 μm)under 1 C discharge rate 进一步考察了颗粒内平均固态锂浓度和颗粒表面的平均表面电流密度,如图10 所示。其中,图10(a)、(c)、(e)根据Fick 定律计算了颗粒内平均固态锂浓度,并将双粒径电极中的大小颗粒内的固态锂浓度分别与相应的单粒径电极中的固态锂浓度比较,从中可以发现,双粒径电极中较小颗粒内的固态锂浓度高于对应单粒径电极内的固态锂浓度,且粒径分布越宽,小颗粒内嵌锂量提升越明显。这是由于当粒径存在分布时,如图9 所示,电解液中锂离子扩散通量增加,靠近集流体侧的小粒径颗粒附近的锂离子浓度较高,从而使得颗粒表面的电化学反应(锂离子嵌入LFP 颗粒)增加,最终使得小粒径颗粒内部的固态锂浓度高于对应的单粒径电极内的固态锂浓度。 图10 1 C 放电时,单粒径与双粒径锂离子电池正极大颗粒与小颗粒平均固态锂浓度[(a)、(c)、(e)]和表面电流密度[(b)、(d)、(f)]随放电时间变化的比较Fig.10 The average solid lithium concentration[(a),(c),(e)]and surface current density[(b),(d),(f)]of the large and small particles in the positive electrode of the lithium ion battery with single−sized and bimodal−sized particles during the discharge time under 1 C discharge rate 同时,图10(a)、(c)、(e)也显示,双粒径电极的大颗粒内固态锂含量比对应单粒径电极的固态锂含量低。为了解释这一现象,通过Butler−Volmer 动力学方程计算了双粒径锂离子电池中大小颗粒表面的平均表面电流密度,结果如图10(b)、(d)、(f)所示。从中可以看出,一方面,双粒径电极表面电流密度分布不均匀,大小颗粒表面电流密度存在差异,引起电池极化,放电过早结束;另一方面,大颗粒内固态锂的扩散速度本身因传质路径变长而减慢,使得其内部固态锂嵌入量更少。 从本文的模拟结果来看,双粒径电极的两种颗粒粒径差异较大时不利于提高性能,(1.5&6.0)μm的双粒径电极的电化学性能比(1.5&4.0)μm 的差,且比1.5 μm 单粒径电极的电化学性能也差。图10(b)、(d)、(f)显示,双粒径电极中,两种粒径差异越大,大小粒径表面的电流密度差异越大,电极表面电流密度分布越不均匀,电池极化加剧,使得电压过早地降到2.5 V以下,从而能量密度降低。这一结果与Lee 等[25]的研究结论非常相似,他们利用扩展的P2D模型研究了非均匀颗粒尺寸对LiCoO2电池性能的影响,模拟结果表明,活性材料中大颗粒含量越高,电极内的锂离子浓度分布越不均匀;同时隔膜与集流体间的电位差增大,导致电压降增大,可用能量降低。 综上,电极活性材料的颗粒存在适当的粒径分布能对电解液中锂离子的扩散有一定的改善,从而增加了小粒径颗粒内固态锂的嵌入量。但是,不同粒径的颗粒表面电流密度和内部固态锂浓度存在差异后,会造成电极内部固态锂浓度分布的不均匀和电极表面电流密度的不均匀,从而引起电池极化的加剧,导致电压降增大,放电结束时大粒径颗粒内未能嵌入足量的固态锂。因此,需要选择适当的粒径分布范围,使得在改善电解质内锂离子扩散情况的同时,不引起过多的极化,最终达到提升电池性能的目的。 本文采用异构模型结合Newman 模型模拟了LFP 锂离子电池的放电过程,考察了单粒径和双粒径活性材料颗粒构成电极的锂离子电池的内部传质过程,并定量分析了不同粒径活性颗粒内的传质情况及其对电池性能的影响,研究结果表明: (1)采用异构模型结合Newman 模型可以更好地模拟锂离子电池工作,直观地反映电极材料颗粒内和颗粒间的传质差异及其对电池性能的影响。 (2)对单一粒径电极的异构模型的模拟计算表明,粒径的减小可以减小LFP 固相扩散系数对电池性能的影响,但会增加锂离子的液相扩散阻力。 (3)对双粒径电极的异构模型的模拟计算表明:电极活性材料颗粒的粒径分布可以促进锂离子在电解液中的扩散,提高小颗粒的锂嵌入量,但会引起极化增大,导致大颗粒的锂嵌入量降低。电池的能量密度由粒径总体大小和分布宽度决定,总体粒度越小,宽度分布适中,能量密度越大。 符 号 说 明 c1——电极颗粒上金属锂浓度,mol/m3 c2——电极内锂离子浓度,mol/m3 Di——电解质或者金属锂的扩散系数,m2/s F——法拉第常数,96487 C/mol I,ii——电流密度,A/m2 jn——电极表面的局部电流密度,A/m2 li——电池各部分厚度,m Nx——电解液中理离子通量的x分量 Rp——正极活性颗粒粒径,μm T——温度,K t——时间,s t+——锂离子电迁移数 U——电池电压,V V——电池体积,m3 WV——体积能量密度,W·h/L x——距离负极集流体的距离,m αi——转移系数 ν+——每摩尔电解质解离生成锂离子的量,mol 下角标 n——负极 p——正极 s——隔膜 1——固相 2——电解质相
1.2 模型方程
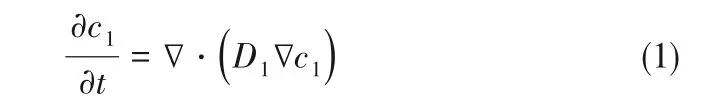

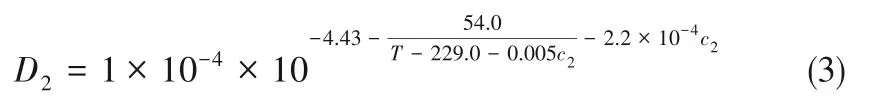
1.3 模型参数与计算

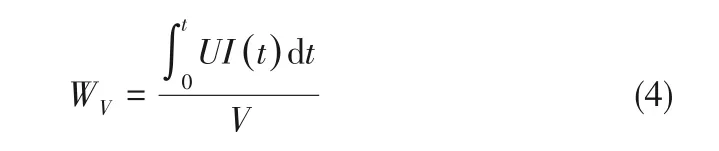
2 结果与讨论
2.1 模型验证
2.2 单粒径锂离子电池模拟结果分析
2.3 双粒径锂离子电池模拟结果分析



3 结 论
