基于GBDT 的串联结构微电网与电网交互稳定性评估

张津京，王兴贵†，宋汶秦，杨维满

（1.兰州理工大学电气工程与信息工程学院，甘肃兰州 730050；2.国网甘肃省电力公司经济技术研究院，甘肃兰州，730050）

微电网是分布式电源（distributed generation，DG）接入电网的一种有效手段.相比于DG 和负荷在馈线上横向分布的并联结构微电网，本文讨论的微源逆变器串联微电网（micro-grid with series micro source inverters，SMSI-MG）输出的电压和电流具有更好的正弦度，同一输出电压等级下可有效降低各微源直流侧电压[1-3].类似的逆变器串联结构因其高输出电压、低dv/dt、高效率等优势而在光伏并网系统中获得广泛应用[4-5].SMSI-MG 系统则在此基础上将不同类型的DG 进行整合，可进一步提高可再生能源利用率.

目前，微电网中的大部分电源均为使用并网变流器作为接口的DG，在并网运行时会由于变流器的高频开关特性而产生大量谐波，污染电网.进一步地，变流器与变流器之间、变流器与电网之间的谐波交互作用也可能引起谐振，导致网侧电压/电流谐波幅值持续放大、严重畸变，进而造成保护装置误动、变流器控制环失稳等，严重影响系统的安全稳定运行[6-7].这种变流器接入电网后的谐波不稳定现象早在2014 年就引起了丹麦Aalborg 大学F.Blaabjerg课题组的关注[8-9].之后，国内外学者对谐波振荡引起的交互系统稳定性问题进行了大量研究[10-11]，但主要针对弱电网环境下的单台逆变器或多台逆变器并联的系统，对SMSI-MG 这种微源逆变器（micr-source inverter，MSI）串联的系统研究较少.SMSI-MG 中MSI 与MSI 之间、串联的MSI 与电网之间同样存在谐波交互作用.特别地，当微源因故障或出力受限进行投切操作后，SMSI-MG 与电网之间的交互作用更加明显，也更加复杂.由于谐波振荡引起的交互系统不稳定具有一定的危害性，因此对其提前进行估计和防范具有重要意义.

从研究方法来说，目前对并网运行系统稳定性进行分析时主要采用状态空间法[12-13]和阻抗分析法[14-15].然而时频域的分析方法存在模型复杂、计算速度慢、实时性差等问题，无法在微源投切后短时间内进行分析决策.近年来，基于数据的机器学习在电力系统暂稳评估研究中取得了重大进展[16-17].机器学习方法将稳定性评估看作一个分类问题，通过离线自动学习建立物理量与稳定后果之间的映射关系.集成学习方法则将几种机器学习技术组合成一个预测模型，可减小方差，改进预测效果[18].其中，基于树模型的集成学习方法梯度提升决策树GBDT 更是在Kaggle、KDD（knowledge discovery in database）等一系列数据挖掘竞赛中受到广泛关注.考虑到微源投切对SMSI-MG 和电网交互稳定性影响机理不明、传统方法无法及时决策等问题，本文借鉴现有电力系统暂稳评估思想，提出一种基于GBDT 的交互稳定性影响评估方法.在建立机器学习模型时，特征提取是关键.因此首先通过分析微源投切与系统输出电压之间的关系，提出特征提取和构造方法.该方法同时考虑到了系统拓扑结构发生变化时所建模型的适应能力，通过简单地拟合即可使模型适应于新网络拓扑，具备良好的泛化性能.最后对所建模型进行了测试.

1 微源投切特征构建及稳定性分级

图1 为并网运行模式下SMSI-MG 系统拓扑.风力、光伏等微源直流侧配备储能装置，通过对其有效控制可抑制功率波动从而保证各MSI 直流侧电压相等.H 桥MSI 输出端串联，系统输出的多电平电压经简单滤波后即可具有较好的正弦度.正常运行时，单相微源数目为n.三相系统由单相系统组合而成.为描述方便，将单相包含n 个微源的三相SMSI-MG 系统简记为n-SMG.该系统在公共耦合点（point of common coupling，PCC）处接入电网.采集PCC 处电压电流经控制器和载波移相SPWM 调制（carrier phase shifted SPWM，CPS-SPWM）后实现对各MSI 的控制，从而使系统输出满足电网调度和负荷需求.微源投切通过开合开关SC 实现.

图1 并网运行模式SMSI-MG 系统拓扑Fig.1 System equivalent topology of grid-connected SMSI-MG

1.1 输入特征构建

利用机器学习训练交互稳定性评估模型，就是要建立输入特征与交互稳定状态的映射关系，因此输入特征的选取和构建是首要的步骤.在对微源投切引起的交互稳定性影响进行评估时，若将三相所有微源的投切状态作为特征属性，则对于一个n-SMG 系统，仅该部分特征维数就为3n.遍历各种投切工况将产生“组合爆炸”问题，而在设置训练样本时则易出现大量相似或是遗漏工况，导致训练模型欠拟合、泛化性能差.为避免上述问题，本文对投切工况Sl（l=1，2，…，L）构造如下特征函数：

1）三相微源平均投切率

投切微源的数目直接影响运行微源的数目，进而影响系统输出电压中基波和谐波的含量.为使模型具备迁移能力，定义投切工况Sl对应的A 相切除微源比例为δac，恢复投入的微源比例为δap，则δap≤δac.令δa=δac-δap为A 相微源投切率，其余两相同理.由于A、B、C 三相微源投切对交互系统稳定性的影响是等价的，因此为了弱化具体相特征对模型泛化能力的影响，定义工况Sl对应的三相微源平均投切率为

2）三相微源投切不平衡度

定义工况Sl对应的三相微源投切不平衡度为

将特征αl和βl结合既可获得Sl对应的三相投切微源数目信息，同时也使特征维数由3 个δj（j 代表A，B，C 三相，下文中含义相同）降为2 个.

3）三相微源投切平均离散度

单相SMSI-MG 采用CPS-SPWM 调制方式.若相邻载波水平移相2π/N，N 个两电平经过水平移相叠加后可得输出电压谐波表达式为[19]

式中：M 为调制度；Jn（·）为n 阶Bessel 函数；ω0为基波角频率，nω0表示基波倍数的谐波；ωc为载波角频率，mωc表示载波倍数的谐波.

将图1 中A 相微源按其MSI 串联顺序依次标记为MS1、MS2、…、MSn，若微源MSi 被切除，则第i个两电平输出为0，其余两相同理.取N=10，m=1，n=2，t=0，假设仅A 相微源进行表1 中投切操作，而δb=δc=0，分别计算各Sl下式（3）中求和项的结果及方差如表1 所示（为分析方便，对求和结果取绝对值）.

表1 不同投切工况下求和项计算结果Tab.1 Calculation results of summation terms under different switching conditions

表1 中，数据①为切除2 个微源的情况，其中一个为MS1，另一个则相对MS1 的位置不同.由式（1）、（2）可知5 种Sl下αl和βl相同.但5 组求和结果的方差较大，由于此时式（3）中其他变量相同，因此可知被切除微源之间的相对位置不同时，uo差异较大.数据②、③进一步说明了这一点.由此可以推断对于n-SMG 系统，当αl和βl相同时，若投切微源之间的相对位置不同，则系统输出电压电流中的谐波含量差异较大，其对交互稳定性的影响程度必然不同.这是采用CPS-SPWM 调制的串联结构系统中特有的现象.因此投切微源的位置应当作为一个与投切数目同样重要的输入特征参与交互稳定性的评估.

为提取工况Sl对应的j 相投切微源之间的相对位置特征，首先构造投切数组ARlj.如图2 所示，微源仍按其MSI 串联顺序标记为MS1、MS2、…、MSn.切除微源在图中用虚线框表示，如A 相的MS1、MS2和MS3.对应于ARlj中，将其序号i 列出，而未切除的微源则标记为0，故此时ARla=[1，2，3，0，0，…，0]，其余与之同理.在获得ARlj后，构造对应的离散度函数用于表征投切微源之间的相对位置.该离散度函数应当满足：1）投切微源之间相对位置变化规律相同则离散度相同；2）δj相同的情况下，切除连续序号的微源越多则离散度越小.据此构造如下所示工况Sl对应的j 相投切微源离散度函数为

式中：Rlj为工况Sl对应的j 相投切微源集合；njc为此时投切微源的总数，定义为对应的投切微源中心，如图中星号所示；njs为投切微源序号连续的次数，即（ARlj[i+1]-ARlj[i]=1）的次数.

图2 ARj构造示意图Fig.2 Diagram of constructing ARj

与特征αl的考虑一样，定义三相平均离散度表征工况Sl对应的投切微源相对位置，即

4）三相微源投切中心欧氏距离

同样取N=10，m=1，n=2，t=0，对A 相微源进行投切操作，而δb=δc=0.计算若干投切微源之间相对位置相同时求和项的结果如表2 所示.

表2 fj（ARlj）相同时求和项计算结果Tab.2 Calculation results of summation terms when fj（ARlj）is the same

表2 中，数据①为切除连续2 个微源的情况，5种Sl下被切除微源之间相对位置相同，因而由式（4）计算得到的离散度相同.数据②和③同理.但三组数据求和结果方差均较大，这说明即便投切微源数目相等、相对位置相同，uo还会因为投切微源的绝对位置不同而产生较大差异，因此需要进一步补充其他特征对其进行区分.观察表2 中各Sl发现，αl、βl和γl相同的情况下，投切微源中心μ 是不同的，故利用离散度结合中心点的方式即可较好地表征及区分不同的微源投切位置.显然该方法可推广至n-SMG 系统及类似采用CPS-SPWM 调制的串联结构系统.为了进一步降低特征维数，定义工况Sl对应的三相微源投切中心欧式距离为

式中：μj的定义同式（4）.

对于一个投切工况Sl，通过上述四个特征即可获取其对应的投切微源数目和位置信息，且特征维数从3n 个投切状态减少为4 个，这对提高模型训练效率有重要作用.

1.2 交互稳定性分级

基于阻抗的并网系统稳定性研究表明，并网运行系统阻抗与电网阻抗之间的动态耦合决定了交互系统的稳定性.当两者阻抗幅值相交处相位裕度较小或过大时，交互系统易出现阻抗交点频率附近的特定次谐波振荡，从而导致交互系统不稳定，而此时并网电流中相应谐波分量会因此而表现为增大至超过其限值[14-15，20-22].SMSI-MG 中微源投切后，其输出阻抗必然发生改变，在假设运行环境其他参数不发生变化的情况下，交互系统稳定性、并网电流谐波分量都会因此而发生改变.为避免复杂的序阻抗测量及相位裕度计算，本文通过提取并网电流中的谐波分量衡量交互系统稳定性.同时，为了充分利用机器学习处理多分类任务的优势，不同于传统方法仅有稳定和不稳定两个状态，本文在稳定和不稳定之间设置临界状态，从而对交互系统稳定性进行更细致和直观的划分.

假设投切工况Sl时PCC 处三相电流中谐波分量为Thl，按照我国GB/T 14549—1993 电能质量标准要求所得谐波电流分量的标准值为Thl-sta，定义各次谐波超限比为ξhl=（Thl-Thl-sta）/Thl-sta；依据ξhl将交互系统稳定性划分等级如下

式中：h 代表谐波阶次；ξlow1、ξlow2为设定的25 次以下谐波电流超限比阈值；ξhig1、ξhig2为25 次以上谐波电流超限比阈值；Wl=1 时谐波电流分量均在限值以下，说明交互系统稳定裕度充足，系统稳定，该种投切工况不会对系统安全稳定运行造成影响；Wl=2表示较稳定，此时特定次谐波电流分量有较小幅度的增加，交互系统可能存在轻微谐振；Wl=3 时特定次谐波电流分量超过限值较多，说明交互系统稳定裕度低，系统进入不稳定状态.为与Wl=4 区分，称此时为较不稳定等级，这时通过调整控制方式可对Sl引起的谐波振荡进行抑制；Wl=4 时特定次谐波电流含量超过50%，交互系统失稳，且并网电流严重畸变，在系统运行过程中应禁止出现该种投切工况.

为了有针对性地调整较不稳定情况下的控制策略，及时抑制或消除微源投切引起的谐振，对该谐振的频率范围进行预测是有必要的.对此，将Wl=3 的样本对应的谐波频段作为预测目标，构建如下分类器.

式中，HBl=1 代表造成交互系统不稳定的谐振发生在低频段；HBl=2 则代表高频段；HBl=3 代表既存在低频谐振也存在高频谐振.

2 用于交互稳定性评估的GBDT 算法

2.1 GBDT 分类算法

梯度提升决策树[23]（GBDT）是一种基于决策树的集成学习方法，其基本思想是每轮迭代中通过拟合残差来学习一个CART 回归树模型T（x；θm），使得损失函数逐步减小.

对于具有K 个类别的训练样本，GBDT 学习算法框架如图3 所示.采用One vs Rest（OvR）分类方法将类别进行one-hot 编码，对每个编码输出分别建立决策树进行迭代.有监督的机器学习通常通过损失函数衡量预测值与真实值之间的偏差，模型训练的目标是损失函数值尽可能小.多分类GBDT 学习算法采用对数损失函数，即

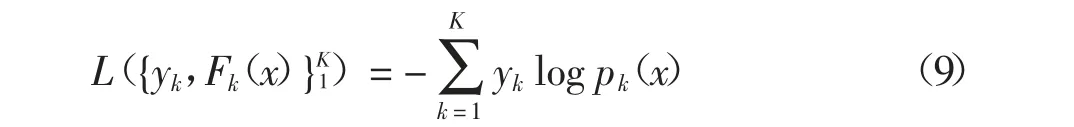
图3 GBDT 多分类模型框架Fig.3 Frame of GBDT multi classification model

第t -1 轮迭代后，第k 个分类器的负梯度误差为

该误差是样本l 对应类别k 的真实标记和t-1轮GBDT 预测概率的差值，即残差.为使损失函数进一步减小，将（xl，r（t-1），k）作为第t 轮、第k 个分类器中决策树的训练数据，如此迭代，直到模型准确度无法再提高时停止，获得最终的GBDT 模型.

为防止过拟合，通过正则化项及子采样的方式提高模型泛化能力.其中，正则化项通过为每个弱学习器加上权重缩减系数v，弱化单个学习器的效果，从而提高模型整体的性能.加入正则化项后GBDT 模型第t 轮迭代输出为

另外，GBDT 模型中弱学习器之间存在依赖关系，其训练过程是串行进行的，但通过无放回抽样可实现部分并行训练，从而提高模型泛化能力及训练效率.

2.2 SMOTE 过采样

微源投切后交互系统中稳定和失稳样本较少，类别比例不平衡，这将导致分类结果准确率较低.对此，本文采用合成少数类过采样（synthetic minority oversampling technique，SMOTE）方法[24]使原始数据中的类别比例更合理.该算法采用kNN 方法在少数类样本的k 个近邻中随机挑选N 个样本进行随机线性插值，并与原数据合成产生新样本.

图4 为部分样本采用SMOTE 方法前后的类别分布对比图.其中，原始样本中Wl=1 的样本比例为11.7%，Wl=3 的样本占到51%，Wl=4 的样本则仅占7.3%.经过SMOTE 处理之后，原本占比较少的类别1 和3 的样本分别在其k 近邻内通过插值产生了与其类别一致的新样本，从而使得这两类样本数量明显增多，最终3 类样本比例趋于平衡.

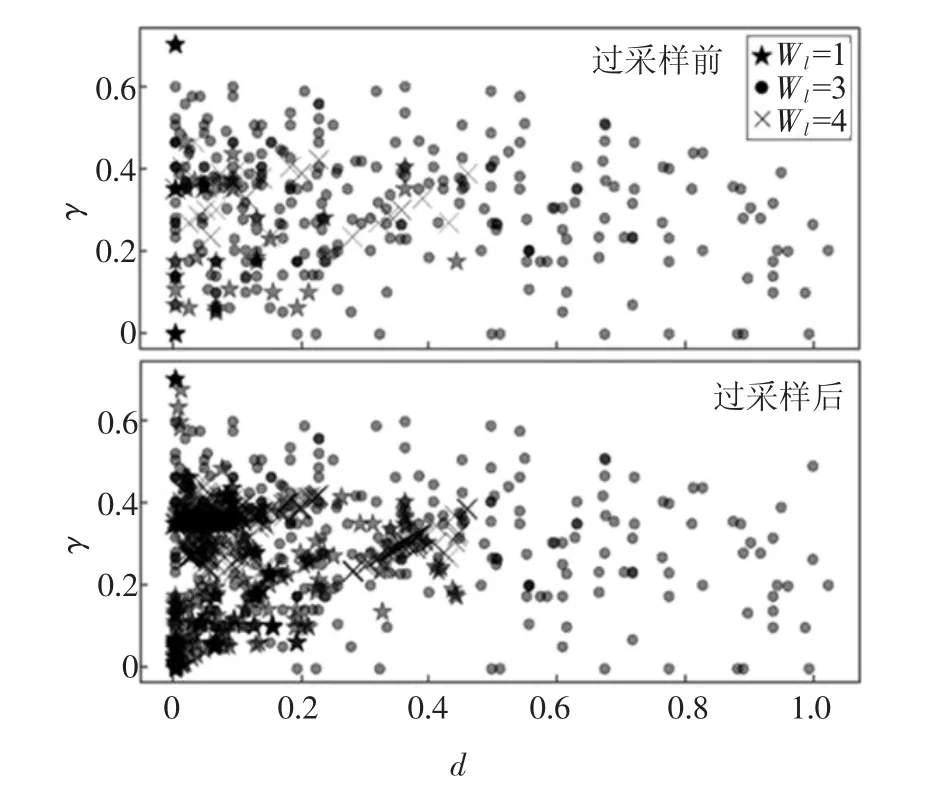
图4 SMOTE 前后样本类别分布对比Fig.4 Comparison of sample category distribution before and after SMOTE

2.3 评价指标

交互稳定性分析中，若将较不稳定和失稳样本（Wl=3，Wl=4）错判为稳定，将导致交互系统失稳前运行人员不采取任何控制或禁止措施，从而给系统造成严重破坏.相比较而言，此种误判比将稳定样本误判为失稳样本带来的影响要大得多.因此，模型评价指标除考虑准确率Acc外，还更加关注较不稳定和失稳样本的精度、召回率以及F1值.多分类器混淆矩阵如表3 所示.

表3 交互稳定性评估多分类器混淆矩阵Tab.3 Confusion matrix of interactive stability evaluation classifiers

表3 中，T1、T2、T3、T4分别为稳定样本、较稳定样本、较不稳定样本和失稳样本被正确预测的数量；Fpa（p=1，2，3，4；a=1，2，3，4）分别为预测为类别p 而实际为类别a 的错误分类的样本数量.

模型准确率表示正确分类的样本数占总体样本数的比值，即

较不稳定样本和失稳样本的精确度、召回率以及F1值定义为

较不稳定样本中的谐振频段预测混淆矩阵如表4 所示.

表4 谐振频段预测多分类器混淆矩阵Tab.4 Confusion matrix of resonant frequency band predicton classifiers

定义模型谐振频段预测准确率为

3 仿真分析

3.1 样本生成

通过对10-SMG 系统中各种预想投切工况进行大量仿真，获取样本数据.仿真中，为保证投切前后并网运行电流方向不变，取αl≤43.3%.另外，以初始状态为基准，设定电网阻抗和滤波电感变化范围为±25%.控制器采用准比例谐振，其比例系数变化范围为0.01～0.5.谐波电流超限比阈值设定为：ξlow1=1.2，ξlow2=8，ξhig1=1.5，ξhig2=45.经过筛选后获取1 000 组样本数据，并以其中70%作为训练样本集，30%作为验证样本集.

为保证测试样本的均匀性，利用线性变换对属性值进行归一化处理

式中，Xmin和Xmax分别为某特征属性的最小和最大值.

3.2 不同模型仿真结果对比

为验证模型评估和预测效果，将GBDT 模型与其他常用机器学习模型的评估结果进行对比.测试模型均基于开源机器学习库Scikit-learn 搭建[25].参数使用五折交叉验证的方法获取最优值，GBDT 模型的正则化通过超参数n_estimators、learning_rate 和subsample 实现；支持向量机（SVM）使用多项式核函数.采用式（12）～（18）定义的评价指标，得到验证集上的测试情况如表5 所示.其中，GBDT 表示使用未经SMOTE 处理的训练数据得到的模型，除此之外的模型均采用过采样后的样本数据；谐振频段预测则使用原始样本中Wl=3 的样本.

表5 不同模型评估和预测结果对比Tab.5 Comparison of assessment and prediction results of different models

表5 中，GBDT 和RF 为集成学习器，其余为个体学习器.对比发现，集成学习器总体比个体学习器拥有较高的准确率；同样是集成学习器，RF 和GBDT准确率相同，但GBDT 在类别3 上具有较高的F1值，且谐振频段预测准确率较高.未经过采样的GBDT 模型评估准确率最低，可见样本类别平衡对提高模型准确率有重要作用，由此也证明了结合过采样方法的必要性和有效性.总体看来，结合SMOTE 的GBDT 模型可实现交互系统稳定性和谐振频段较高准确率的评估和预测，这也从另一个方面说明了特征提取方法的正确性.

3.3 模型迁移能力验证

为验证所建模型的适应性，设置微源数目n 从5至40 以5 为步长变化，分别建立n-SMG 并网运行系统仿真模型，且新拓扑系统保持与10-SMG 直流侧总电压相等.各系统分别对30 种不同投切Sl进行仿真构成240 个新建测试样本.由于微源数目n 不同，在利用式（5）、（6）计算投切微源位置特征属性值时，会出现与10-SMG 系统规律相同但属性值不同的情况，使得之前构建的GBDT 模型应用于n-SMG（n≠10）系统时会发生误判.因此对于n-SMG（n≠10）系统，首先需要对特征γ 和d 进行映射，使其与10-SMG 的数值相对应.

选取若干具有代表性的点对[xn-SMG，x10-SMG]，通过线性拟合获得新拓扑系统和10-SMG 在特征X 下的对应关系g（X），如图5 所示的20-SMG 与10-SMG系统中的g（γ）和g（d）.之后将g（X）应用于新拓扑下的其他样本，即可获得映射后的特征属性值.通过该映射方法，分别得到n-SMG 修正后的特征值，通过之前所建GBDT 模型进行交互稳定性分级评估和谐振频段预测，验证结果如表6 所示.其中10-SMG的投切样本是原始样本中未出现的投切工况.

图5 20-SMG 与10-SMG 中γ 和d 的映射关系Fig.5 The mapping relationship between γ and d in 20-SMG and 10-SMG systems

表6 模型迁移能力验证Tab.6 Verification results of model migration capability

从表6 可看出，所建模型应用于5-SMG 和10-SMG 时，测试准确度较高.而应用于n>10 的系统时，由于γ 的非线性映射以及训练样本的缺失，准确率有所下降，但后期通过补充样本可望进一步提高准确率.总体来看，所建模型通过特征属性的简单拟合即可适用于新拓扑系统，避免花费大量时间重新生成样本，具有一定的实际应用价值.

基于GBDT 的交互稳定性评估主要由离线训练和在线评估两部分构成.通过前期数据集生成、离线模型训练和模型性能评估，可获得训练好的GBDT模型.在线评估时通过在线获取微源投切等特征数据，并将特征数据输入（根据系统拓扑结构，映射或直接输入）训练好的模型，即可对相应投切操作引起的交互稳定性进行评估，并预测谐振频段，为预防控制提供及时有效的决策依据.

4 结论

本文将机器学习用于微源投切后的SMSI-MG与电网交互稳定性分析，提出一种适用于串联结构系统的微源投切特征提取方法，并采用GBDT 模型进行交互稳定性评估和谐振频段预测.得到如下结论：

1）对于采用CPS-SPWM 调制的并网运行SMSI-MG系统，其与电网的交互稳定性不仅与投切微源数目相关，还与投切微源的位置相关.通过三相微源平均投切率、投切不平衡度、投切平均离散度、投切中心欧式距离四个特征函数即可提取三相投切微源的数目和位置信息.而通过对后两者的拟合，模型即可具备良好的泛化和迁移能力.特征提取方法正确，模型训练效率高.

2）将微源投切对交互系统稳定性的影响划分为4 个类别，类别划分更细致，且对较不稳定样本中的谐振频率范围进行预测，避免了传统方法中的谐振检测.模型输出为多类别、多标签，对后续决策更具实时性和指导性.

3）采用结合过采样的集成学习方法，与其他个体学习器的评估方法相比，保证了较高的总体评估和预测准确性.模型泛化能力强，具有实用价值.

本文所提基于机器学习模型的交互稳定性评估方法无需建立复杂的数学模型，为并网运行系统稳定性在线分析及决策提供了新思路，同时所提出的特征提取方法也可为类似串联结构系统在电能质量分析、优化运行等方面提供方法参考.在今后的研究中，除进一步扩大样本规模外，还需寻找更优的指标将微源投切对交互系统的影响量化呈现出来，以进一步提高模型的实际应用价值.