考虑流固耦合的泵闸组合闸门结构自振特性研究

2021-03-05沈远航朱召泉

中国农村水利水电 2021年2期

沈远航，朱召泉

(河海大学土木与交通学院，南京 210098)

随着城镇化建设的发展，传统泵闸站由于闸站分离，存在工程投资高、过水断面小，不利于水体交换等缺陷，无法满足日益增长的城市水质治理与防洪排涝需求。新型泵闸组合闸门结构是将潜水轴流泵安装在平面钢闸门上，闸门既可挡水也可作为水泵的支承体系。其工作原理是当外河水位较高时，关闭闸门防止河水倒灌，当内河水位达到设定高度时开启水泵强排水；当内河水位较高时，开启闸门，河道重力自流，实现汛期的防洪排涝。当内河水位较低或流速不足时，开启水泵，将外河水补充至内河，实现枯水期的补水。与传统闸站相比，新型泵闸组合闸门结构可大大节省建设用地，降低土建施工成本，增强内、外河之间水系的连通，便于管理。

20世纪七八十年代，我国在南通、嘉兴等地的沿江圩区进行了闸站结合的早期实践尝试，如扬州市某圩口闸是由立式电动机和抢排泵通过角钢框架固定在悬搁式闸门上而成，可用于低水头排涝[1]。近年来，关于闸站组合的研究主要关注其工作原理、施工工序及施工关键点等方面，尉鉴洋[2]设计制作的一体化移动泵站被应用于绍兴市的区域性污水治理；周明等[3]提出了泵闸组合闸门结构在设计及施工时尤需关注重量布置问题，以免起吊偏重；2018年福州茶河亭建成了我国首套智能泵闸系统，三渠道三泵闸，采用一闸配一泵的形式，闸门尺寸为2 m×5.62 m(宽×高)[4]，表明一体化泵闸可有效解决河道水动力不足问题，有助于河道排涝。目前，尚无将水泵与大、中型水闸相结合的实践成果，且关于水泵布置对闸门结构耦合特性的影响尚无深入的研究，因此有必要对新型泵闸组合闸门结构的动力特性进行数值模拟分析。

根据国内外钢闸门事故的调查显示，闸门低阶自振频率与水流高能脉动频率重合而引起的低阻尼共振很可能导致闸门结构发生破坏[5]。新型泵闸组合闸门结构较为复杂，为保证其安全工作，有必要考虑水流脉动或闸门缝隙渗漏水等对闸门自振特性的影响。鉴于此，利用ANSYS建立水体-泵闸组合闸门结构耦合模型，采用非对称算法进行结构动力特性研究，分析水位变化与水泵布置方案等因素对泵闸组合闸门结构自振特性的影响，可为新型泵闸组合闸门结构的设计提供理论依据。

1 流固耦合设置

钢闸门的振动与周围水体的波动属于典型的流固耦合问题[6]。设δ为闸门结构的节点位移矢量，δf为流固接触面处的结构位移，p为动水压力，可依据拉格朗日第二类方程推导得耦合系统的振动控制方程[7]为

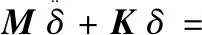
(1)

式中：M、K分别为闸门结构的质量矩阵、刚度矩阵。

将水闸前后流场模拟为无黏性且不可压缩的水体时，扰动压力p满足▽2p=0。可用组合系数为D的流固交界面上节点加速度的线性组合来表示动水压力Pf，即Pf=Df。引入Pf与p之间的转换矩阵S，δ与δf之间的转换矩阵T，可得到：

(2)

式(2)即为流固耦合振动方程，其中Mp=SDT为附加质量矩阵。

目前，国内外研究常采用建立真实水体模型方法考虑接触界面流固耦合作用。本文采用ANSYS有限元软件对水体-泵闸组合闸门结构耦合模型进行分析，通过FSI命令将闸门面板、主纵梁及横隔板腹板与水体相交的面标记为流固耦合界面，以耦合结构运动与流体压力[8]。

2 泵闸组合闸门结构流固耦合有限元模型

2.1 数值计算模型

依据设计要求，泵闸组合闸门结构上、下游的最高水位分别为6.0和5.5 m，总体尺寸(宽×高)为11.0 m×6.2 m，面板厚度为10 mm，主纵梁采用变截面工字梁，横(竖)隔板采用T型截面梁，边梁采用双腹式截面。门叶结构布置的具体尺寸如图1所示，各主要构件截面尺寸如表1所示。采用700QZ型潜水泵，进水口直径为920 mm，主纵梁及横隔板上加设支撑板以固定泵体。

表1 泵闸组合闸门结构主要构件截面尺寸 mmTab.1 Cross-sectional dimensions of main components of the pump-gate combination gate structure

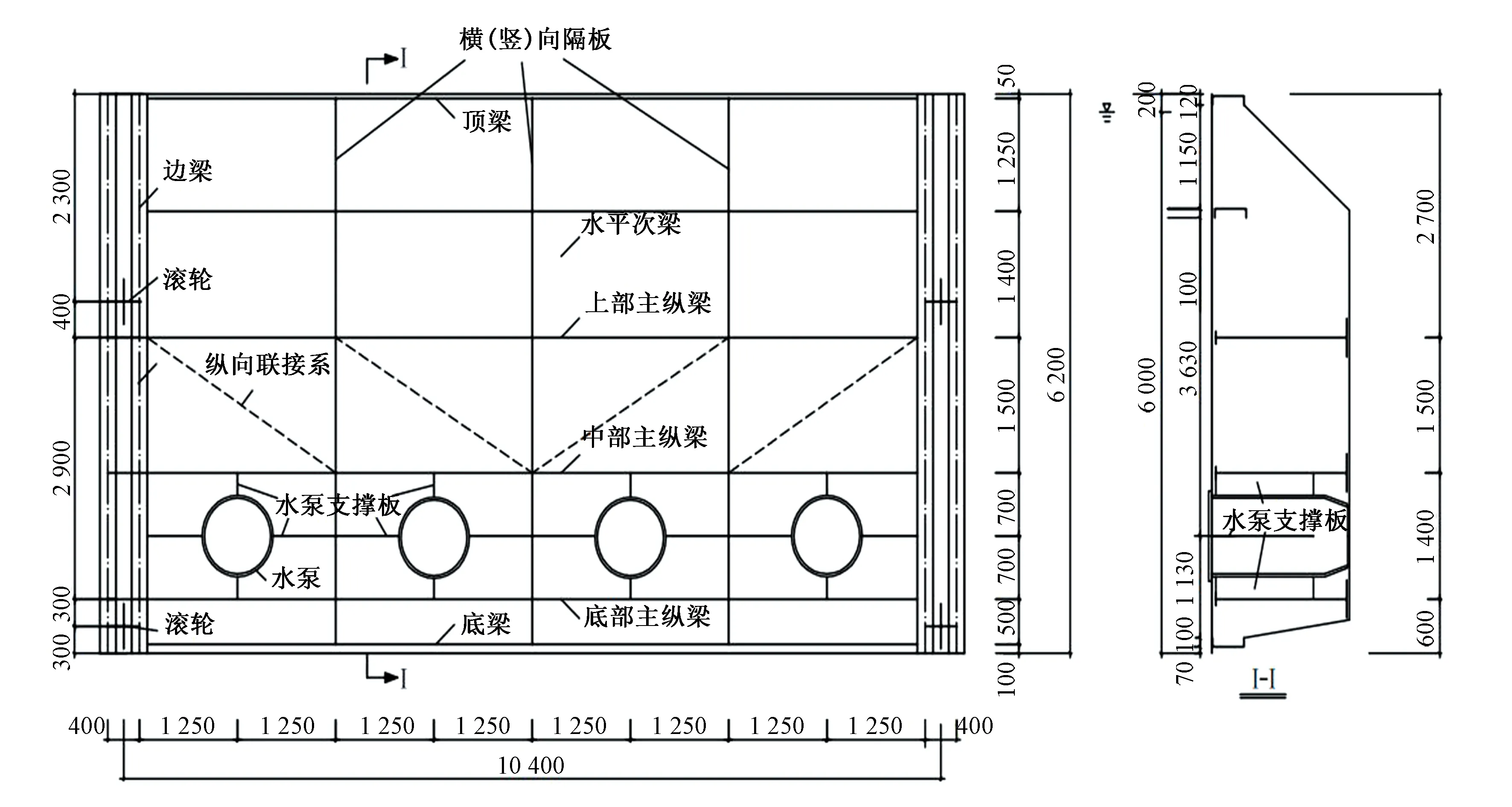
图1 泵闸组合闸门结构梁格布置尺寸图(单位：mm)Fig.1 Diagram of beam layout and size for the pump-gate combination gate structure

根据闸门的几何特征和受力机理，面板、纵横梁等构件采用shell63单元模拟，纵向连接系的杆件采用link180单元模拟，在底主纵梁下部沿闸门跨度方向布置的四台潜水泵均采用solid45单元简化模拟为与实际厚度相符的圆管。水体模型选用fuild30三维流体单元，水体耦合长度取为闸门高度的10倍[9]，即62 000 mm。采用有限元前处理软件Hypermesh建立水体-泵闸组合闸门结构耦合模型如图2所示。

图2 水体-泵闸组合闸门结构耦合模型Fig.2 Coupling model of the water body and the pump-gate combination gate structure

2.2 约束条件

考虑门槽两侧止水影响，边梁模拟为简支情况，即一侧边梁设置沿闸门跨度方向x向的弹性链杆约束，两行走支承滚轮处设置顺水流向z向的简支约束；关门工况下，考虑底止水作用，面板底部设置竖向y向仅能受压的约束；开门工况下，释放露出门槽部分的边梁节点的各项约束，两边梁顶端吊点处设置弹簧约束，以模拟吊绳(杆)作用，并依据不同开度时的吊绳长度设置其刚度系数为K=EA/l，式中：E为吊绳弹性模量，A为截面面积，l为吊绳长度。考虑河床和闸墩侧墙的限制，水体两侧及底部定义为固壁条件[10]，上表面定义为自由液面。

2.3 计算参数

闸门采用Q235钢材，弹性模量E=206 GPa，泊松比μ=0.3，密度ρ=7 850 kg/m3；水泵采用铸铁材料，弹性模量E=105 GPa，泊松比μ=0.33，为模拟每台水泵真实的泵体重量约2 500 kg，按其泵口直径和壁厚，取其等效材料密度值为ρ=21.5×103kg/m3；水体密度ρ=1 000 kg/m3；初步设计采用2根三股直径22 mm的钢丝绳，即A=1 140 mm2。

3 泵闸组合闸门结构流固耦合自振特性分析

3.1 关门状态下泵闸组合闸门结构的流固耦合自振特性分析

采用Lanczos法求解不考虑流固耦合作用时泵闸组合闸门结构的自振频率和振型；采用非对称法求解不同水位下水体-泵闸组合闸门结构耦合模型的自振频率如表2所示，部分代表性工况下的结构第一阶振型如图3所示。

(1)从表2可看出，不考虑闸门结构与门前后水体的流固耦合作用时，闸门结构自身各阶自振频率较高，均大于14 Hz。当考虑流固耦合作用时，随着闸门前后水位的升高，结构自振频率逐渐降低。当上游水位低于2 m时，因流固耦合作用较弱，闸门结构的第一阶自振频率略有降低；当上游水位达到5 m以上时，闸门受流固耦合作用影响已很明显，闸门结构的第一阶自振频率已降低到3.885 Hz，落至水流脉动的主频率区[11]，即0～5 Hz范围内，易引发共振；当上游水位为6 m，下游水位升至5.5 m(最高水位)时，结构第一阶自振频率降到最小值2.772 Hz。

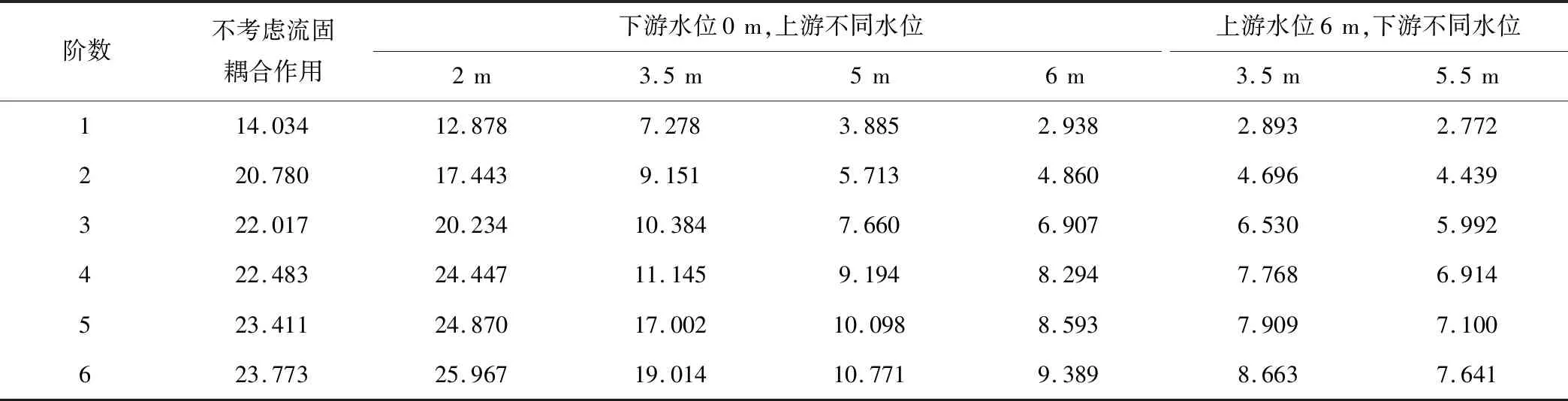
表2 关门状态不同水位下泵闸组合闸门结构的各阶自振频率 HzTab.2 Natural vibration frequency of closed pump-gate combination gate structure under different water levels

(2)由图3可以看出，随着闸门耦合水体水位的变化，闸门结构的振型模态也随之变化。在不考虑流固耦合作用时或上游水位较低为2 m时，结构的第一阶振型如图3(a)所示为外部约束较弱的竖向整体振动；当上游水位升至3.5 m时，由于水体耦合深度明显增大，耦合作用显著，闸门的第一阶振型如图3(b)所示转变为门叶主纵梁间区格面板顺水流向的前后振动；随着闸门前后水位进一步升高，流固耦合作用越发明显，最高水位下的结构第一阶振型如图3(c)所示，大部分面板区格产生顺水流向的前后振动。若增大面板厚度为16 mm时，可使同水位条件下结构的第一阶自振频率提高为5.362 Hz。但考虑到面板重量占闸门总重比例较大，不宜使其厚度过大。

图3 关门状态不同水位下泵闸组合闸门结构的第一阶振型图Fig.3 First-order mode diagram of closed pump-gate combination gate structure under different water levels

3.2 开门状态下泵闸组合闸门结构的流固耦合自振特性分析

根据泵闸组合闸门结构的工作原理，在汛期时可通过开启闸门进行泄洪。分析上游水位为6.0 m，下游水位分别为0、3.5和5.5 m 3种水位组合下，闸门开度1 m(0.15)、闸门开度2.5 m(0.4)和闸门开度4 m(0.65)时的泵闸组合闸门结构自振特性，可得各工况下闸门各阶自振频率如表3所示，部分代表性工况下结构的第一阶振型图如图4所示。

(1)由表3可知，考虑流固耦合作用时，相同水位条件下，随着闸门开度的增大，闸门上的水体耦合范围减小，结构的自振频率增大；相同开度下，闸门前后耦合水体的深度越大，结构的自振频率越低，故▽上6.0 m，▽下5.5 m工况下闸门开度为1 m时结构的第一阶自振频率最低，为3.575 Hz。当闸门开度小于2.5 m时，结构的第一阶自振频率均小于5 Hz，落入水流脉动主频率区，故对小开度泄流时，需注意此类泵闸组合闸门的流激振动问题。

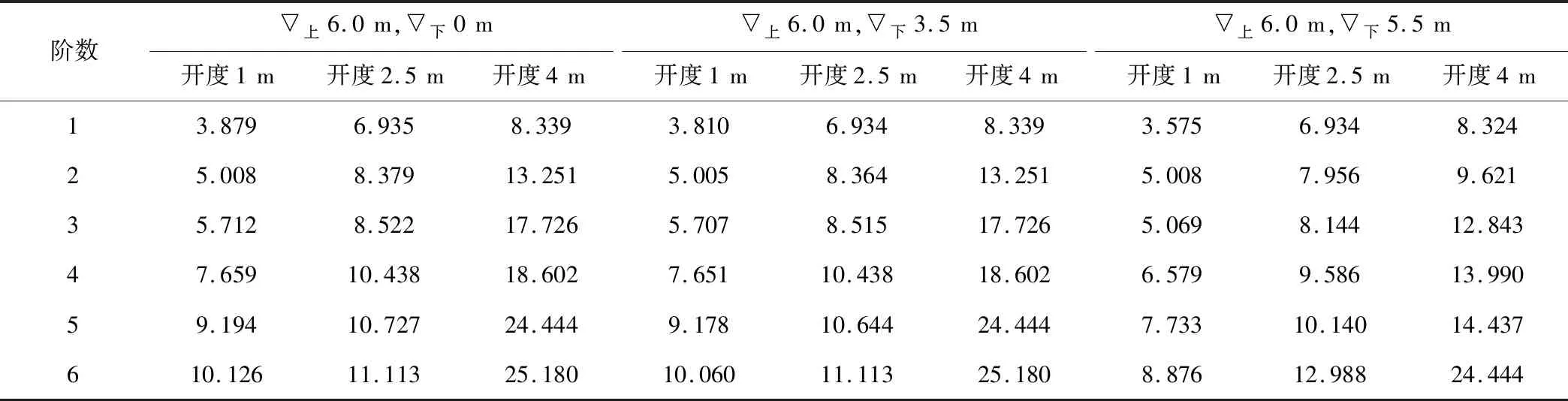
表3 不同开度泵闸组合闸门结构的各阶自振频率 HzTab.3 Natural vibration frequency of pump-gate combination gate structure with different openings

(2)以▽上6.0 m，▽下5.5 m工况为例分析结构各阶振型可知，当闸门开度为1 m时如图4(a)所示，由于受流固耦合作用影响显著，结构的第一阶振型为门叶中上部区格面板沿水流向的前后振动；当闸门开度为2.5 m时如图4(b)～图4(d)所示，由于流固耦合作用略有减弱，结构的第一阶振型转变为沿竖向的整体振动，第二至第五阶振型仍均为门叶中上部面板的前后振动，第六阶振型为闸门整体的弯扭振动伴随中部区格面板的鼓曲；当闸门开度在4 m以上(接近全开)时如图4(e)～图4(f)所示，由于门体上耦合水体范围较小，流固耦合作用较弱，因开门时闸门的外部约束减弱，结构的前几阶振型均表现为整体振动：第一阶振型为竖向振动，第二阶和第三阶振型均为闸门沿竖向的弯扭振动，第四阶振型为闸门沿水流向的弯曲振动，第五阶及以后高阶振型主要是闸门局部区格面板沿水流向的弹性振动。

图4 ▽上6.0 m，▽下5.5 m，不同开度泵闸组合闸门结构的代表性振型图Fig.4 Representative mode diagrams of pump-gate combination gate structure with different openings when the upstream water level is 6m and the downstream water level is 5.5 m

4 水泵布置方案对泵闸组合闸门结构自振特性的影响分析

为满足泵闸站不同的流量需求，可在平面钢闸门上安装二至四台潜水泵。前文计算了门体结构上布置四台水泵时的闸门自振特性，下面计算集中和分开布置两台水泵时的情况，以最高水位组合▽上6.0 m，▽下5.5 m为例，分析水泵布置方案对闸门结构自振特性的影响，结果如表4和图5所示。

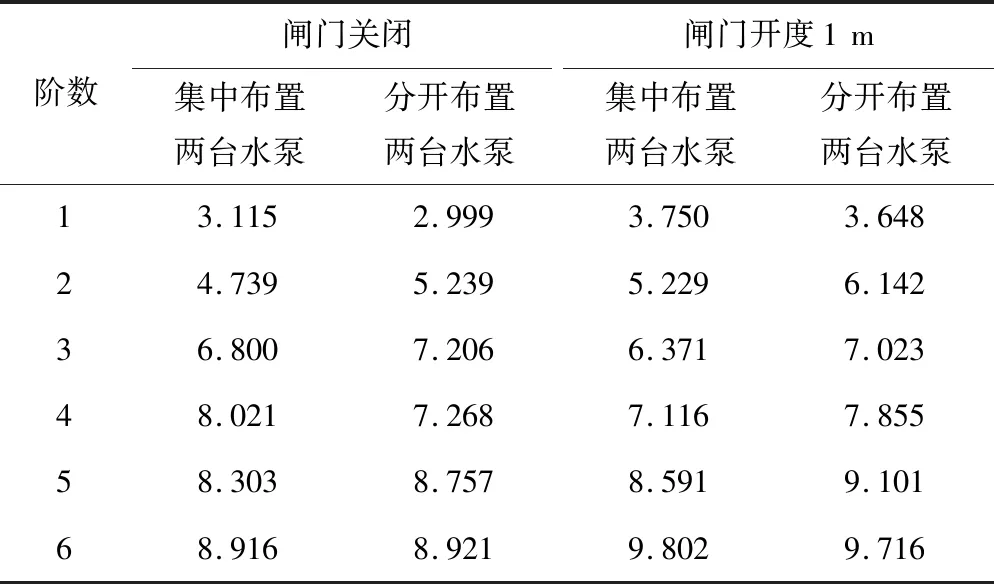
表4 ▽上6.0 m，▽下5.5 m，关门状态下布置两台水泵的泵闸组合闸门结构的各阶自振频率 HzTab.4 Natural vibration frequency of closed pump-gate combination gate structure with two pumps when the upstream water level is 6m and the downstream water level is 5.5 m

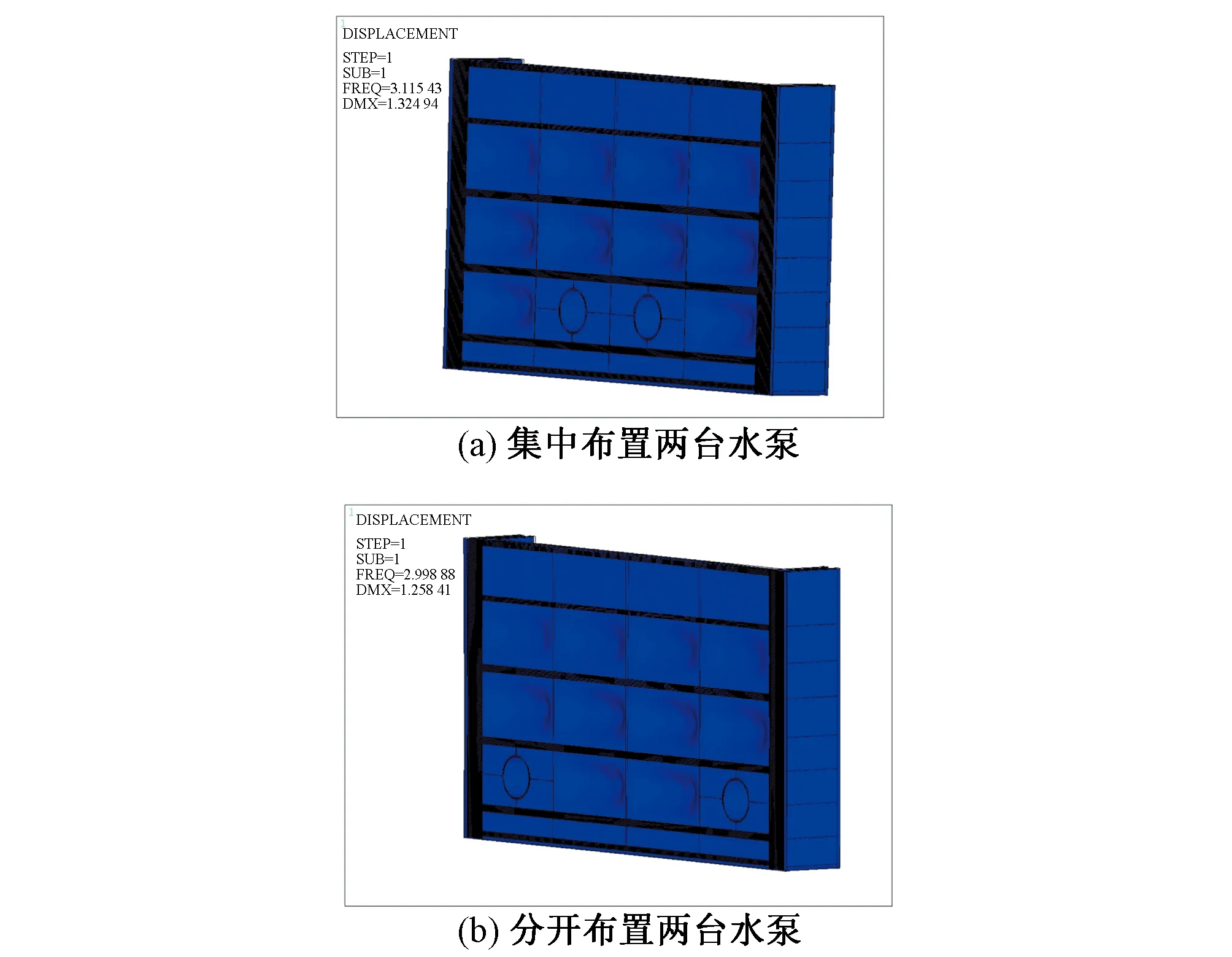
图5 ▽上6.0 m，▽下5.5 m，关门状态下不同水泵布置方案的泵闸组合闸门结构的第一阶振型图Fig.5 First-order mode diagram of closed pump-gate combination gate structure with different pump layouts when the upstream water level is 6m and the downstream water level is 5.5 m

(1)表2、表3为布置四台水泵的情况，表4为布置两台水泵的情况，对比可知，考虑流固耦合作用时，水泵布置个数越多，泵闸组合闸门结构的整体质量越大，故闸门自振频率越低。如▽上6.0 m，▽下5.5 m关门状态下，布置四台水泵的闸门结构第一阶自振频率为2.772 Hz(见表2)，而集中和分开布置两台水泵的闸门结构第一阶自振频率分别为3.115和2.999 Hz(见表4)。

(2)由图5可以看出，水泵布置方案对闸门振型有显著的影响，未布置水泵的区格面板有较为明显的局部振动。集中布置两台水泵时结构第一阶振型如图5(a)所示，闸门下主纵梁间未布置水泵的两端区格面板产生较明显的局部振动，但考虑到闸门两侧闸墙处止水的弹性约束作用，因此结构各部位的振动特性相对均衡；分开布置两台水泵时结构第一阶振型如图5(b)所示，相较而言，闸门中间两区格面板沿水流向的局部振动更加强烈。