线性多胞体微分包含解的通有稳定性*

计 伟

(贵州建设职业技术学院信息管理学院，贵州 贵阳 551400)

微分包含又称多值泛函微分方程，属于非线性分析理论的一个重要分支，是描述自然界不确定性常用方法之一.围绕微分包含的研究，主要集中于微分包含解的存在性、稳定性和其他定性理论.无论是在微分包含(含线性多胞体微分包含)研究，还是在其他科学研究中，与解的稳定性相比，存在性的获得比较容易.实际分析中，在获得解的存在性但解不唯一时，应该选择哪个解；或者，研究问题的环境或参数发生微小改变，对解有什么样的影响：这都是本质问题.如非合作博弈论中，Nash均衡点存在性与稳定性的问题就是这方面的例证.

关于非合作博弈论Nash均衡的稳定性研究，尤其是通有稳定性(从整体上考察问题对象发生扰动时，对应的解集怎么变化)研究，学者取得了丰硕的研究成果.1962年，Wu等[1]对有限N人非合作博弈首先引入了本质Nash平衡点的概念.1963年，Jiang[2]进一步对有限N人非合作博弈首先引入了Nash平衡点集本质连通区的概念，并证明了对任何有限N人非合作博弈，其Nash平衡点集至少存在1个本质连通区.1986年，Kohlberg等[3]应用代数几何方法证明了每个有限博弈的Nash平衡点集由有限个连通区组成，且其中至少有1个是本质的.1999年，Yu[4]研究了n人非合作博弈的本质均衡.1998年，Yu等[5]应用集值分析方法证明了Baire纲意义下微分包含解集具有通有稳定性.关于微分包含的结果还可参见文献[6]及其所引用的文献.受文献[5-6]的启发，笔者拟在恰当假设下构造一个问题空间M，并在M上引入度量η，使(M,η)构成一个完备度量空间，然后引入问题的本质解定义，利用集值映射方法对线性多胞体微分包含解的通有稳定性展开讨论.

1 预备知识

设N是有限正整数，Ui⊂RN×N(i=1,2,…,N)是有界闭凸集，Ai∈Ui(i=1,2,…,N)是实矩阵.设[0,T]是一个时间区间，对于∀t∈[0,T]，有x(t)∈RN.对初始对(0,x0)，考虑如下微分包含的Cauchy问题[7]：

(1)

其中

co(Aix(t))={Ax(t)|A∈co(Ai,i=1,2,…,N)}.

这里

即Γ是RN中的一个标准单纯型，且在第一卦限中是一个闭凸集.例如，当N=2时，Γ是连接(1,0),(0,1)的一条闭线段；当N=3时，Γ是连接(1,0,0),(0,1,0),(0,0,1)的一个闭三角形.显然，co(A1,A2,…,AN)是由{Ai,i=1,2,…,N}组成的凸包，且是一个闭集.

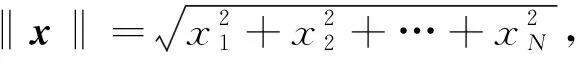
引入如下假设条件：

(ⅰ)对于∀A∈co(Ai,i=1,2,…,N),∃L>0,s.t.‖A‖≤L；

(ⅱ)对于任意充分小且大于0的ε1及∀ξ∈R,有|ξ|≤ε1；

(ⅲ)对于任意充分小且大于0的ε2及∀μ1,μ2∈RN,有‖μ1-μ2‖≤ε2.

设

M={V∈co(Ai,i=1,2,…,N)|V满足(ⅰ),(ⅱ),(ⅲ)}.

对于∀V1,V2∈M，定义Hausdorff度量

η(V1,V2)=h(S1,S2)+|ξ1-ξ2|+‖μ1-μ2‖，

其中

S1,S2⊆{A∈co(Ai,i=1,2,…,N)|,∃L>0,s.t.‖A‖≤L}，

这里

容易证明(M,η)是一个完备度量空间.

构造线性多胞体微分包含问题(1)的解集S(co(Ai))，

S(co(Ai))={x(t)∈C([0,T]；RN)|x(t)是线性多胞体微分包含的解}.

S定义了一个从M→2C([0,T]；RN)集值映射，记为S:M→2C([0,T]；RN).

本研究的目的是获得线性多胞体微分包含问题(1)的解集关于右端部分co(Ai)，以及初始数据(ξ,μ)同时发生扰动时的稳定性.主要是借助文献[5-6]及其所引用文献的思想，在Baire纲分类意义下，讨论问题(1)的解的稳定性，即一种通有稳定性.

定义1[8]令S(V)(∀V∈M)是一个非空集合，对于C([0,T]；RN)中的任意开集G，G⊃S(V)(G∩S(V)≠)，若存在V的任意开领域O(V)，使得对于有则称集值映射S在V上半连续(下半连续).若集值映射S在V既上半连续，又下半连续，则称S在V连续.若对于∀V∈M，集值映射S在V上半连续(下半连续、连续)，则称S在M上半连续(下半连续、连续).

定义2[8]若S(V)(∀V∈M)是一个非空紧集，且S在V上半连续，则称S是一个上半连续紧映射.

引理1[8]若M是完备度量空间，则必是Baire空间.

定义3称Graphh(S)={(V,x)∈M×C([0,T]；RN)|x∈S(V)}为S的图像，若S的图像Graph(S)是闭的，则称集值映射S为闭映射.

引理2[8]若集值映射S:M→2W是闭的，且W是紧集，则S是一个上半连续映射.

定义4[8]设Q⊂M，若Q包含M中一列稠密开集的交，则称Q是M中的剩余集.

引理3[9](Fort定理)若M是一个完备度量空间，集值映射S:M→2U是一个上半连续紧映射，则存在M中的一个稠密剩余集Q，使得对于∀V∈M，S(V)下半连续，从而连续.

2 通有稳定性

定理1∀V∈M,S(V)≠.

证明在M中任意取定V，由Michael连续选择性定理[10]可知问题(1)实际上转化为常系数的线性微分方程组问题，再由微分方程基本理论可知该问题的解必定存在，故S(V)≠.

定理2集值映射S:M→2C([0,T]；RN)是上半连续紧映射.

证明因C([0,T]；RN)是紧集，故由引理2可知只需证明集值映射S的图是闭的，即证明：若对于∀Vn∈M,有Vn→V,对于∀xn(t)∈S(Vn),有xn(t)→x(t),则x(t)∈S(V).

首先证明S(V)的相对紧性.若对于∀t∈(0,T)，t1,t2∈[t-h,t+h]，有

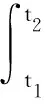
则存在A∈co(Ai)，使得

‖x(t2)-x(t1)‖≤‖A‖|t2-t1|，

于是{x(t):x(t)∈S(V)}是等度连续的.同理存在A∈co(Ai)，使得

‖x(t)‖≤‖x0‖e‖A‖T.

因此{x(t):x(t)∈S(V)}是一致有界的.由Ascoli-Arzela定理[11]可知S(V)相对紧.

然后证明S(V)是闭的.设xn(t)∈S(Vn)且xn(t)→x(t)，则对于∀t∈(0,T)，t1,t2∈[t-h,t+h]，有

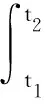
且

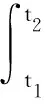
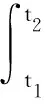
为了研究线性多胞体微分包含的通有稳定性，引入如下定义：

定义6若对于∀x(t)∈S(co(Ai))，x(t)都是问题(1)的本质解，则称S(co(Ai))是本质的.

定理3∀V∈M是本质的，当且仅当集值映射S:M→2C([0,T]；RN)在V下半连续.

证明设∀V∈M，对于任意开集G⊂C([0,T]；RN)，G∩S(V)≠，可取x∈G∩S(V).由本质解的定义，x∈S(V)是本质的，存在V开领域O(V)，使得对于有而因此所以S在V下半连续.

反之，∀V∈M，x∈S(V)，对x的任意开领域G(x)，S(V)∩G(x)≠.由下半连续的定义，存在S开领域O(V)，使得对于有可取则而因此x必是本质解，从而V是本质的.

定理4M中存在一个稠密剩余集Q，使得对于∀V∈Q，V是本质的.

证明因M是完备度量空间，故由引理1可知它必是Baire空间，再由定理2可知S是上半连续紧映射，于是由Fort定理和定理3可知结论成立.

注1由定理4可知，对于∀V∈M，因Q在M中稠密，故V可以由本质解作任意逼近，再由Baire纲定理可知Q是第二纲的，因此在Baire纲分类意义下，对于大多数V∈M，V是本质的，即在M中具有通有性质.