广义严格对角占优矩阵的递进式判定新准则*

石 慧，庹 清，吴 乐

(吉首大学数学与统计学院，湖南 吉首 416000)

广义严格对角占优矩阵在经济数学、控制论和矩阵理论等方面都有广泛应用,且许多问题都归结于广义严格对角占优矩阵的数值判定上,而这个数值判定是比较困难的.近年来,众多学者给出了广义严格对角占优矩阵的一些判定准则[1-11].其中,范迎松等[1]运用细分和迭代的思想,通过对矩阵的非占优行指标集进行细分,以及对矩阵的占优行指标集构造递进式正对角因子的方法,给出了一组广义严格对角占优矩阵的细分迭代判别准则.笔者受此启发,拟进一步研究广义严格对角占优矩阵的判定问题,运用细分矩阵的非占优行指标集和构造递进式新正对角因子的方法,给出广义严格对角占优矩阵的递进式判定新准则.

1 基础知识

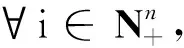
(3)若存在正对角矩阵X,使得AX∈D,则称A是广义严格对角占优矩阵,也称为非奇异H-矩阵.记广义严格对角占优矩阵的全体为D*.

定义2[4]若A∈D0,并对于满足|aii|=Λi的下标i都存在非零元素链aij1aj1j2…ajsj满足|ajj|>Λj,则称A为具有非零元素链的对角占优矩阵.

引理1[3]设A=(aij)∈Cn×n,是具有非零元素链的对角占优矩阵,则A为广义严格对角占优矩阵.

引理2[3]设A=(aij)∈Cn×n,是不可约对角占优矩阵,则A为广义严格对角占优矩阵.

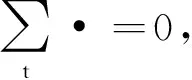
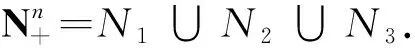
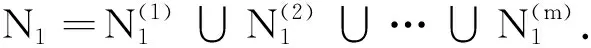
引理3[1]设A=(aij)∈Cn×n.若∃l∈N,使得

则A为广义严格对角占优矩阵.

引理4[2]设A=(aij)∈Cn×n.记

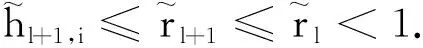
则A为广义严格对角占优矩阵.

由定义1可知,因为找到正对角矩阵X使得矩阵AX∈D,是判定矩阵A为广义严格对角占优矩阵的关键,所以笔者将在文献[1-2]的基础上,通过细分矩阵的非占优行指标集和构造递进式新正对角因子得到新的正对角矩阵.

2 主要结果及其证明

为了叙述方便,记

定理1设A=(aij)∈Cn×n.若∃l0∈N,使得

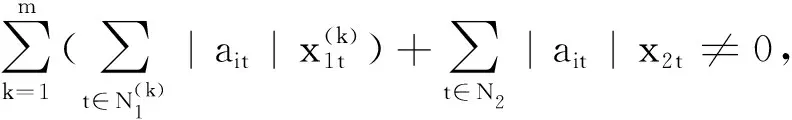
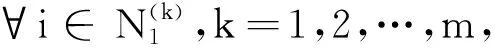
再根据h2,i,r2的定义可知,对于∀i∈N3,有h2,i≤r2≤r1<1.设l=s时,hs+1,i≤rs+1≤rs=1,则当l=s+1时,由于

因此根据hs+2,i,rs+2的定义可知,对于∀i∈N3,有hs+2,i≤rs+2≤rs+1<1.于是由数学归纳法可知

hl+1,i≤rl+1≤rl<1 ∀i∈N3,l∈N.

(1)

对于充分小的正数ε,由条件可知,∃l0∈N,使得ε满足

(2)

(3)

构造正对角矩阵X=diag(x1,x2,…,xn),并记B=AX=(bij),其中

对于∀i∈N2,由(3)式可得

(4)

由(1)式可得

(5)

对于∀i∈N3,由(4),(5)式可得

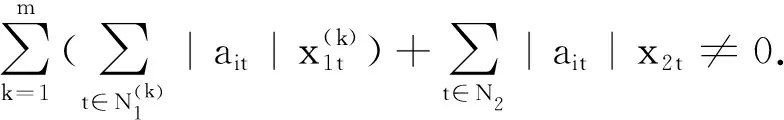
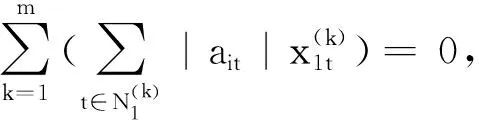
此时,只需验证l=0时,是否满足定理1条件即可.

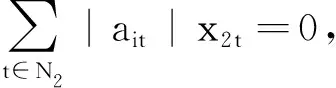
此时,需要依次验证l=0,1,…时,是否满足定理1条件.

定理2设A=(aij)∈Cn×n,且A为不可约矩阵.若∃l0∈N,使得

(6)

(7)

且不等式(6),(7)中至少有1个严格不等式成立,则A∈D*.

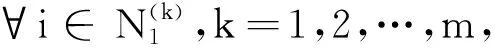
构造正对角矩阵X1=diag(x1,x2,…,xn),并记B1=AX1=(bij),其中

(8)

由(7)式可知,对于∀i∈N2,有

(9)

对于∀i∈N2,由(9)式可得

对于∀i∈N3,由(5)式可得

定理3设A=(aij)∈Cn×n,若∃l0∈N,使得

(10)

(11)

且对于不等式(10),(11)中等号成立的i,都存在非零元素链aij1aj1j2…ajsj满足

则A∈D*.

3 数值算例

例1考虑矩阵A,

取m=3,∀l∈N时,可以验证矩阵A不满足文献[1]中定理1的条件.

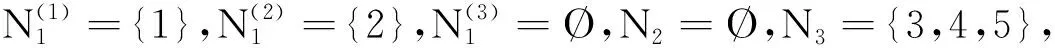
于是

由此可知矩阵A满足定理1的条件,从而A∈D*.

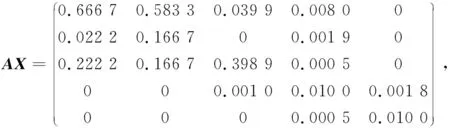
容易证明AX∈D,于是A∈D*.

例2考虑矩阵B,

取m=1,∀l∈N时,可以验证矩阵B不满足文献[8]中定理1的条件.

取m=1,l=0和l=1时,可以验证矩阵B不满足文献[1]中定理1的条件.

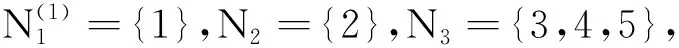
于是

由此可知矩阵B满足定理1的条件,从而B∈D*.

容易证明BX∈D,于是B∈D*.

例3考虑矩阵C,

取∀l∈N时,可以验证矩阵C不满足文献[2]中定理2的条件,且不满足文献[6]中定理1的条件和文献[7]中定理1的条件.

取m=2,l=0或l=1时,可以验证矩阵C满足定理1的条件.

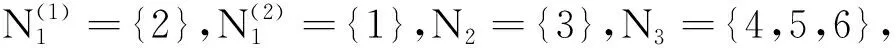
于是

由此可知矩阵C满足定理1的条件,从而C∈D*.

容易证明CX∈D,于是C∈D*.