跨座式单轨弓网耦合主动控制研究
2021-03-05刘朝涛狄科宏杜子学
刘朝涛,狄科宏,杜子学,杨 震
(重庆交通大学 机电与车辆工程学院,重庆 400074)
0 引 言
跨座式单轨交通作为城市轨道交通的一个重要分支,具有爬坡能力强,转弯半径小等优点,已成为重庆市公共交通不可或缺的一部分[1]。跨座式单轨的接触网为刚性接触网,且横向安装在轨道梁的侧壁,其弓网关系为刚体与刚体之间的耦合关系,而刚性接触网的不平顺会产生许多接触硬点。列车通过这些硬点时,受电弓的相对位置与速度会发生瞬态变化,尤其在高速通过时,受电弓会频繁地撞击接触网,一是会造成较大的运行噪声;二是会加大接触力的波动从而加剧弓头与接触网的机械磨损,且长期运行会造成受电弓的断裂影响行车稳定性与安全,不仅降低了其使用寿命,也提高了运行维护成本;三是列车通过接触网硬点时产生的短暂脱弓离线会出现拉弧现象,由此带来的电气磨损不仅会灼伤弓头,同时也会破坏列车电气稳定性从而造成电气元件的损坏。因此,对于受电弓主动控制研究具有很大的意义,同时也是轨道交通电气化发展不可或缺的一部分。
主动控制是基于现代控制理论,在不影响受电弓内部结构参数前提下,使用相关自动化技术对其施加外力来降低弓网接触力波动[2]。目前国内外对于受电弓主动控制的研究均是针对铁路系统的受电弓,而对单轨受电弓主动控制的研究少之甚少。跨座式单轨受电弓相比于其他制式的受电弓设计较为独特。受电弓的底座与框架间安装存在升弓弹簧。该弹簧主要作用是在单轨列车行进过程中为弓网间的接触提供自适应力。而在列车高速行进过程中,升弓弹簧的响应速度非常有限,若受电弓在通过第一个接触网硬点而发生了位移变化,在通过第二个硬点之前没有完成调节,则受电弓与接触网之间极有可能会发生碰撞。因此,需要加入执行机构来进行主动干预与快速调节。笔者所研究的主动控制是以无刷直流电机为执行机构。为了不改变受电弓内部结构参数,笔者将电机与框架连杆直连,考虑到电机的启动以及动态性能,选择双闭环控制器。为了兼备控制精度与控制速度,选择分数阶PID作为系统的控制器。系统整体结构如图1。

图1 系统结构
1 弓网耦合模型
单轨受电弓在结构上与其他受电弓有较大差异,但在工作模式以及动态特性上具有很大的相似性。因此在进行受电弓动力学分析的时候,可参考现有的方法进行分析。考虑到弓网耦合工作在平衡位置时,弓网接触点的动态波动范围不大,因此,可以对受电弓的动力学模型进行线性化处理。
将受电弓框架部分以及弓头部分看作单独的质量块,它们之间以等效的刚度和阻尼相连,便得到了受电弓的二质量归算模型[3]。
跨座式轨道交通接触网的布置形式不同于其他轨道交通的接触网。通过锚段关节连接每一段伸缩单元并固定在轨道梁的侧壁,受电弓则横向安装在轨道列车的底部裙板。单轨列车的弓网耦合系统为横向接触受流,因此可以忽略重力以及空气阻力的影响。
理论上跨座式单轨交通的刚性接触网不存在弹性,但在弓网耦合过程中,接触网在振动的影响下会产生一定的弹性变形,因此笔者在建模时考虑了接触网的弹性特性。同时,考虑到接触网的特殊结构形式,为了方便建模,将支持绝缘子视为刚体。而汇流排与接触线在夹紧力的作用下具有近似相同的动力学特性,可将其视为整体。因此得到的弓网耦合模型如图2。
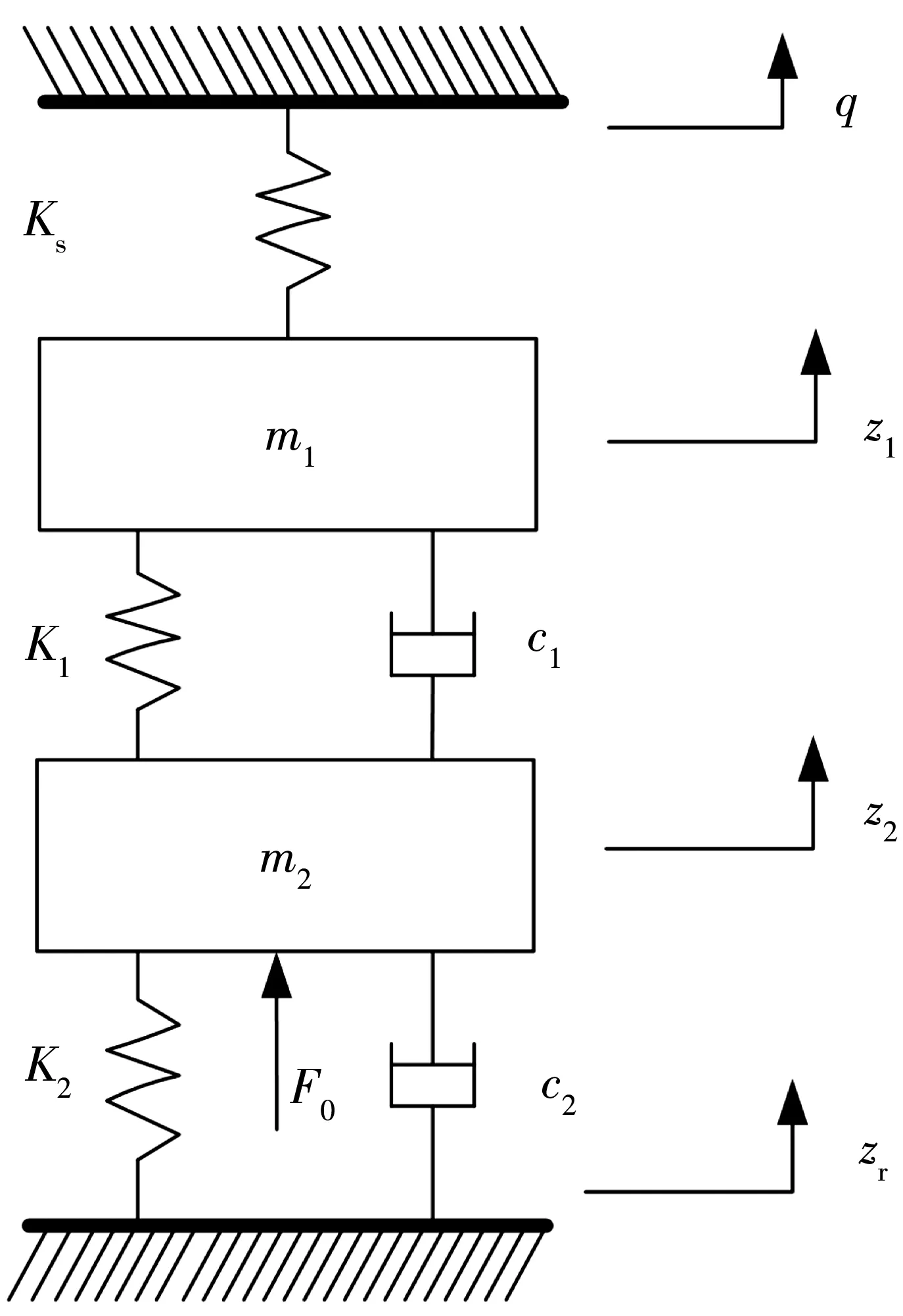
图2 弓网耦合模型
系统的运动微分方程:
(1)
k2(zr-z2)+F0
(2)

(3)
式中:
C=[ks0 0 0]
其中:q与w(t)分别为刚性接触网不平顺与车身振动引起的激励;F0为静态抬升力。
2 三相无刷直流电机的双闭环模型
永磁无刷直流电机相比于传统的直流电机,具有维护成本低、机械效率高、功率密度高、易于控制等优点,已广泛应用于各种工业工程场合[4]。其常用的控制方法有电压直接控制以及电流、转速双闭环控制等。电压直接控制会产生较大的转矩脉动,降低电机运行可靠性,无法应用于高性能要求的场合。而双闭环控制解决了电压控制转矩脉动大的缺点,且具有启动速度快、动态性能好等优点[5]。因此选择双闭环的无刷直流电机控制策略。
2.1 无刷直流电机数学模型
三相星形绕组的无刷支流电机满足条件:
il1+il2+il3=0
(4)
且有:
Mil1+Mil2+Mil3=0
(5)
则定子的电压平衡方程:
(6)
式中:M为相邻两相绕组互感;L为每相的自感。
电机的电磁转矩由永磁转子磁场与定子绕组电流相互作用产生,其数值为通过每相的电磁功率与转子转速之比,表达式如式(7):
(7)
则转子的运动方程为:
(8)
式中:Ω为转子角速度;B为阻尼系数。
2.2 逆变器模型
逆变器为MOSEFT管六臂全桥驱动模型,导通方式为二二导通,不考虑电容保护电路的影响,且假设开关管与二极管具有理想的开关特性。逆变器拓扑如图3。

图3 逆变器拓扑
在某一时刻,l1、l2相导通,此时il3=0。根据三相绕组的电压平衡方程,可得:
(9)
联立可得中点的电压为:
(10)
在换相临界位置,l3相导通,il3>0,并产生反向的感应电动势,此时的电压平衡方程为:
(11)
此时的中点电压为:
(12)
式中:Udc为直流侧电压。通过判断下一时刻换相相的电流可求解不同换相时刻的中点电压,结合感应电动势进而可求得逆变器输出至三相绕组的端电压。
2.3 电流滞环控制模型
电流滞环控制的作用主要是对三相绕组的电流进行跟踪并调节,对绕组起到一定的保护作用,其次是根据电机霍尔传感器的信号以及电流的误差信号输出相应的PWM信号。
当电流的正向误差大于滞环比较器的环宽时,输出对应相正向导通,负向关断的PWM信号;当电流的反向误差低于环宽的边界,输出对应相反向导通、正向关断的PWM信号。因此,电流的调节在滞环环宽内呈锯齿状波动。
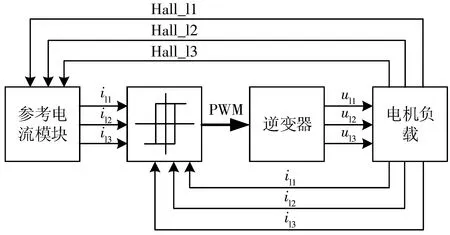
图4 电流滞环控制
2.4 转速环控制模型
转速环换采用PI控制,通过转速误差输出不同的参考电流,实现转速的快速调节以及稳态无静差,同时对负载变化引起的干扰起到一定的抵抗作用。为防止电流过大,需要在参考电流输出位置加入限幅模块[6]。
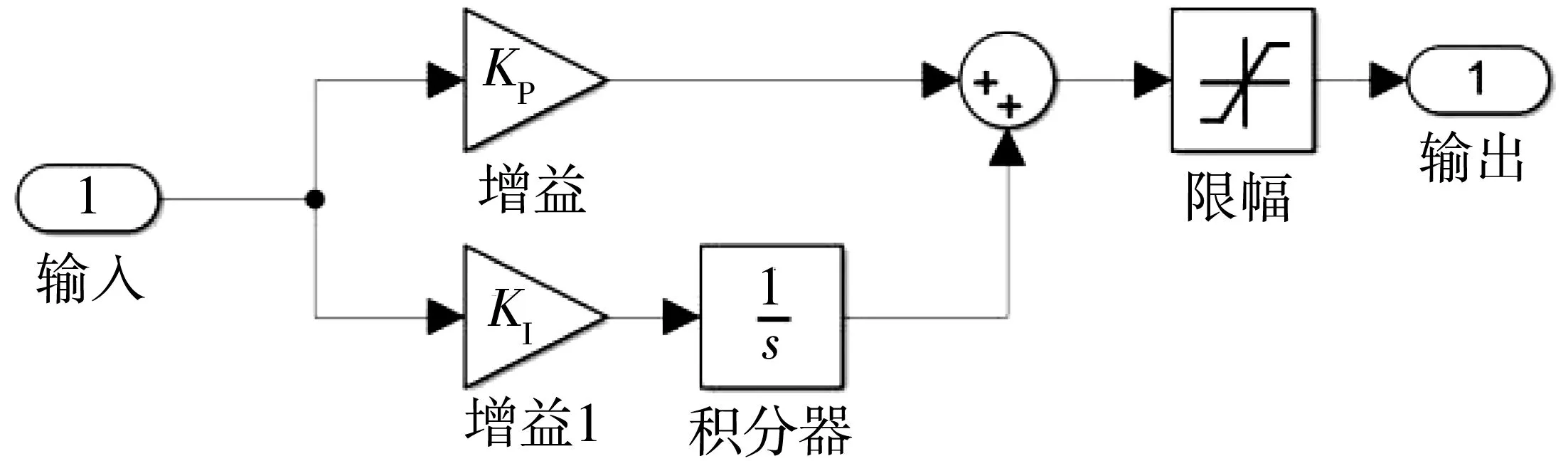
图5 转速换PI控制
3 分数阶PID控制器设计
3.1 分数阶PID模型
分数阶PIλDμ是PID在整数阶微积分的扩展,引入了λ与μ的微积分阶次参数,使得控制系统的调节范围更广,且具有灵活性。相比整数阶PID,其对系统内部的多变量以及非线性因素具有更强的调节特性。因此,分数阶PID控制器具有更好的动态性能及鲁棒性[7]。
分数阶微积分常用的基本函数有Gamma函数、Beta函数和Mittag-Leffler函数,其中Gamma函数定义如式(13):

(13)
Gamma函数满足式(14):
Γ(x+1)=xΓ(x)
(14)
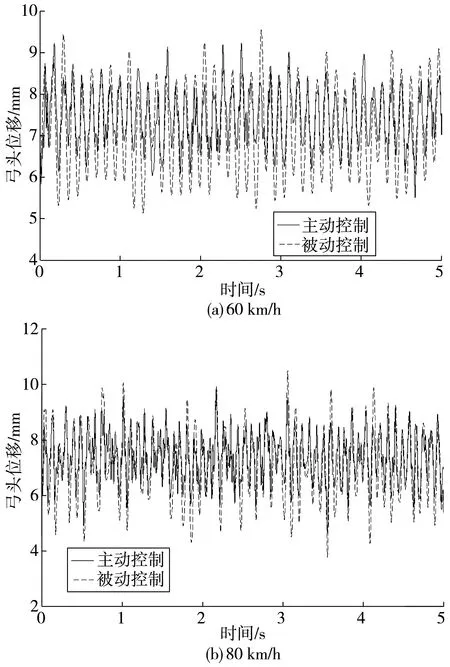
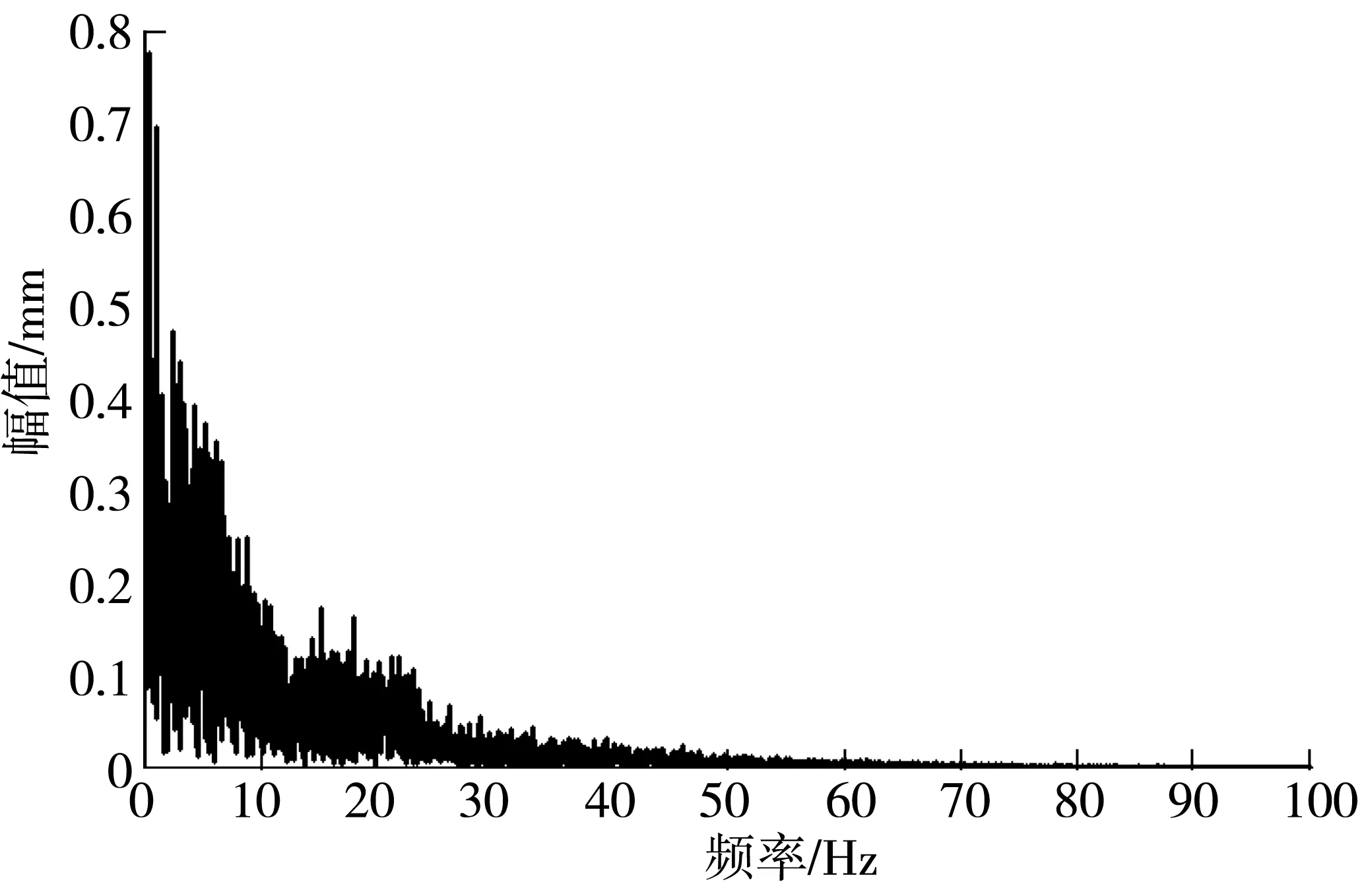
分数阶微积分的定义在整数阶微积分定义基础上推广与归纳而来,是整数阶的一般形式[8]。目前分数阶微积分的定义有3种,分别为Grunwald-Letnikov(GL)定义、Riemann-Liouvile(RL)以及Caputo定义。其中RL是建立在Gamma函数基础上,对于任意实数p,满足m-1 (15) 积分形式为: (16) 拉普拉斯变换同样可以用来描述分数阶控制系统。分数阶PID的传递函数可以描述为: (17) 积分环节能够提高系统的型别,进而增加系统的稳定性。对于整数阶PID,一阶积分环节会带来系统的90°相位迟滞,从而影响系统的动态性能。通过调节积分阶数λ,使得系统的相位滞角在0~180°变化,可以同时兼顾系统的动态性能以及稳定性。微分环节会产生一个超前的90°相角,从而做出误差的提前修正,增加系统的阻尼特性,提高系统的动态性能。同理,通过调节微分阶次μ,使得超前相角在0~180°变化,使得系统阻尼的调节范围更大,从而达到系统的性能要求[9]。 通常计算分数阶系统具有一定的难度,需要将分数阶次近似为整数阶,再利用整数阶的计算方法进行求解,提高计算效率。目前分数阶近似有两种途径,一种是间接近似,另一种是直接近似。直接近似法是将分数阶系统离散化,然后进行求解;间接近似需要在频域内选定合适的频域范围,再通过算法对分数阶进行整定。目前最常用的近似算法为Oustaloup法,该算法通过设计Oustaloup滤波器对输入的分数阶系统进行近似化。假设近似对象[10]: R(s)=sα (18) 选定拟合频段(ωb,ωh)以及近似阶次N,则滤波器的输出高阶传递函数为: (19) 其中增益以及零极点为: (20) 频段的选取标准应能尽量提高精度,但是精度的提高将伴随着计算速度的下降。对于近似的阶次,理论上阶次越高,近似效果越好,但是当拟合阶次达到某一值时,逼近精度将不再有明显的提高。因此,在选取拟合频段以及阶次时应综合考虑系统性能和精度的要求。 对于弓网系统,静态抬升力F0=100 N。升弓弹簧以及弓头支座的橡胶弹簧刚度和阻尼系数参数通过仪器实验测得,分别为k2=12 900 N/m、c2=100 N·s/m、k1=17 000 N/m、c1=200 N·s/m。弓头以及框架的等效质量m1=2.49 kg、m2=10.54 kg。接触刚度ks=8 700 N/m。刚性接触网的支持绝缘子间距L=2 m[11]。激励均看作白噪声,功率设置为10-7。 电机采用双闭环控制,其参数如下:转动惯量J=0.001 56 kg·m2;定子绕组电阻R=4.526 Ω;电感L=0.002 H;阻尼系数B=0.0002 N·m·s/rad;极对数p=2;电源为直流220 V;电流限幅为±30 A;转速环KP=20;KI=0.15;采样周期T=0.000 1 s;积分阶次为0.9;微分阶次为0;控制器的KP=0.08;KI=0.01;近似阶次N=4。 评价弓网受流质量的主要指标有平均接触力、最大接触力、最小接触力、接触力标准差以及离线率[12]。对于跨座式单轨交通,规定弓网接触力的最佳值应在59±10 N之间,而接触力在44~79 N之间便可保证弓网之间的正常受流。 单轨列车安装有多个受电弓,且均匀分布在列车两侧,只取一侧单个受电弓进行分析。受制于跨座式单轨交通特殊的承载方式,列车直线段行驶的最高时速不能超过80 km/h[13]。因此,让列车以60、80 km/h 两种不同速度在直线段匀速行驶,通过对比不同时速下被动与主动控制的接触力响应来分析主动控制对弓网接触力的影响。 图6为直线段不同时速下接触力的时域响应曲线。由图6和表1可知,直线段60、80 km/h时速下弓网离线率均为0;在速度为60 km/h时,控制效果明显,接触力基本稳定在54~68 N之间,接触力的波动明显降低,弓网处于最佳受流状态;而速度为80 km/h时,控制效果相比低速状态要减弱一些,但接触力大部分时间均能稳定在47~72 N之间,能够完成弓网间的正常受流。 图6 直线段不同时速下接触力响应曲线 表1 不同时速下弓网受流质量评价指标统计 图7为直线段不同时速下弓头位移曲线。同理,在速度为60 km/h时,主动控制能明显改善弓头的振动,而在速度为80 km/h时,控制效果随着速度的增加而变弱,原因是随着车速的增加,弓网对于高频信号也愈发敏感,而电机的响应速度为一定值。 图7 直线段不同时速下弓头位移曲线 表2 不同时速下弓头位移评价统计 图8为阶跃输入下电机主动控制的接触力响应曲线,接触力在从0~60 N的上升时间为0.02 s左右。图9为实测截取的重庆轨道交通3号线双龙至碧津直线段70 km/h的弓头位移频响特性曲线。引起弓头振动的频率主要集中在0~30 Hz以内,主动控制的反应速度能够应对该频段内的激励信号。因此,电机主动控制的模型虽然对于高速弓网的调节有些欠缺,但对于跨座式单轨列车,其调节效果能够满足弓网的正常受流。 图8 阶跃输入接触力响应 图9 直线段70 km/h弓头位移频响特性 建立了线性二自由度弓网耦合质量归算模型,以及无刷直流电机的双闭环控制模型,利用分数阶PID控制器模拟并分析了弓网接触力的响应,实验结果表明: 1)在直线段60 km/h下,主动控制的接触力标准差相比被动控制减少了43.3%,弓头位移的标准差相比被动控制减小了35.8%,且接触力基本维持在49~69 N的最佳弓网受流区间;而在80 km/h下,主动控制的接触力标准差相比被动控制减少了30.0%,弓头位移的标准差相比被动控制减小了30.7%,接触力基本维持在44~79 N的正常受流区间,证明所设计的主动控制系统能有效降低接触力波动,改善弓头振动,提高受流质量。 2)在响应速度方面,主动控制的响应时间在0.02 s左右,而根据实测数据,引起弓网振动的频段主要集中在0~30 Hz以内,因此控制系统能够进行快速响应与有效调节,进一步验证了所设计主动控制系统的有效性。3.2 分数阶次的近似
4 仿真实验分析
4.1 系统参数设置
4.2 接触力与弓头位移响应分析




5 结 论
