基于分段式双幂次趋近律的迭代滑模航向控制

赵月林，门茂峰，孙 壮

(大连海事大学 航海学院，辽宁 大连 116026)

滑模变结构控制方法是由前苏联学者在20世纪提出，因滑模变结构控制设计过程简单，对系统干扰和参数摄动具有“完全自适应”性引起了科研界的高度重视[1]。船舶运动系统复杂，其数学模型的不准确易产生摄动，因此滑模变结构控制的“完全自适应性”能很好地解决数学建模中存在的问题，十分适合用来设计航向控制器。然而，滑模变结构控制算法的抖振问题十分严重[2]，该问题一直是国内外学者关注的难点。

笔者选用滑模变结构控制算法对船舶航行控制器进行了设计，提出了一种分段式双幂次趋近律来减弱滑模变结构控制的抖振问题。通过数学求解得出该分段式双幂次趋近律的收敛时间小于快速趋近律和双幂次趋近律。在实验验证中发现趋近律的参数选择很大程度上影响着系统抖振，固定参数很难使控制器达到最佳状态。因此笔者选用简单而又高效的RBF神经网络来在线估计参数，使得控制器参数时时刻刻保持在最佳状态，提高航向控制器效率。

1 趋近律特性分析

滑模变结构控制方法在控制器设计上具有独特的优势，但其抖振现象也给设计者带来了无限困扰。高为炳[3]在运用滑模方法设计控制器时，引入快速趋近律和双幂次趋近律在抖振的削弱方面具有良好效果，但是两者收敛时间不同。为此，笔者在用数学方法对两种趋近律的收敛时间进行求解并进行比较的基础上，提出了一种有效降低抖振、提高收敛速度的分段式双幂次趋近律。

1.1 双幂次趋近律收敛时间分析

双幂次趋近律[4]的表达如式(1)：

(1)

式中：k1>0，k2>0，0<γ<1。

假设s(0)>1，则系统分为两个运动阶段趋近于平衡点；s(0)→s=1，此时为远离滑模面阶段，因为1+γ>1，故趋近律中第1项起主导作用，忽略第2项。

由式(1)可得式(2)：

(2)

对式(2)进行积分，可得式(3)：

(3)

由此可计算得s(0)→s=1，所用时间如式(4)：

(4)

s=1→s=0，接近滑模面阶段。同理，式(1)趋近律的第2项起主导作用，忽略第1项，由式(1)可得式(5)：

(5)

对式(5)两边积分，可得式(6)：

sγ=-γk2t+1

(6)

由此可得s=1→s=0所用时间如式(7)：

(7)

由此可见，收敛速度为两段收敛时间的总和，如式(8)：

(8)

假设s(0)<-1，同理系统亦分两个阶段趋近平衡点，此时收敛时间的证明可参见上述推理。根据上述证明得出收敛时间如式(9)：

(9)

1.2 快速趋近律收敛时间分析

快速趋近律表达如式(10)：

(10)

当s(0)→s=1，快速趋近律中第1项为主导项，同理忽略第2项[5]，由文献[6]可得式(11)：

(11)

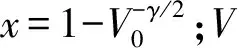
根据文献[4]，在趋近时间上双幂次趋近律小于快速趋近律。由上述分析可知：当s=1→s=0时，快速趋近律的主导项为等式第2项，因此第1项忽略。但该项与双幂次趋近律的第2项相同，故为比较收敛时间长短[7]，必须分析整体时间。文献[8]对式(10)进行求解，得式(12)、(13)：

(12)

(13)

参考文献[9]，对式(13)积分，得式(14)：

(14)

文献[9]通过引入高斯超几何函数，通过作商方法计算出ts1/td1>1，得出s=1→s=0阶段快速趋近律的收敛时间小于双幂次趋近律收敛时间。

1.3 分段式双幂次趋近律

基于上述数学分析，在s(0)>1时，在s(0)→s=1阶段，趋近时间上双幂次趋近律小于快速趋近律，因此选择双幂次趋近律为最佳；而在s=1→s=0阶段，趋近时间上快速趋近律小于双幂次趋近律，因此选择快速趋近律为最佳。鉴于以上不同阶段最佳选项匹配矛盾问题，笔者提出了一种分段式双幂次趋近律来进行分段匹配。分段式双幂次趋近律表达如式(15)：

(15)

式中：b=1+γ；ξ=1；c=1-γ；fal为一种非线性幂次组合函数。

fal的计算如式(16)：

(16)

当运动点远离滑模面，即|s|>1时，式(15)等价于式(1)，该系统以双幂次趋近律形式趋近于滑模面。

当|s|≤1时，式(15)可等价于式(17)：

(17)

该形式较快速趋近律少了后边的幂次项，式(17)其实可称为指数项，其本身可提高收敛速率，极大程度地削弱系统抖振。

为评价该趋近律综合性能，借鉴自动控制原理中的时域分析法进行评价。该系统为一阶系统无超调量，评价指标主要是调节时间。调节时间大小表征系统过渡过程进行快慢。而调节时间主要由时间常数T决定，T越小系统的快速性就越好，1/T即为系统运动最大变化率。为求最大变化率，笔者引入导数求变化率思想，即在极小范围内两点间变化量可等价于该点导数，也称为斜率。因此在快速趋近律中变化趋势最快处取A(0.008,-0.096 28)、B(0.01,-0.085)两点，求得1/T1=5.5，故T1=0.18；同理，因双幂次趋近律与分段式双幂次趋近律变化趋势相同，所以同取C(0.011,-0.099 87)、D(0.013,-0.084 1)两点，求得1/T2=8，故T1=0.12。由T1>T2，所以分段式双幂次趋近律与双幂次趋近律快速性较好，如图1、2。由图 1、2可看出：分段式双幂次趋近律在趋近于零点时基本无抖振，曲线平滑。

图1 快速趋近律、双幂次趋近律、分段式双幂次趋近律的比较

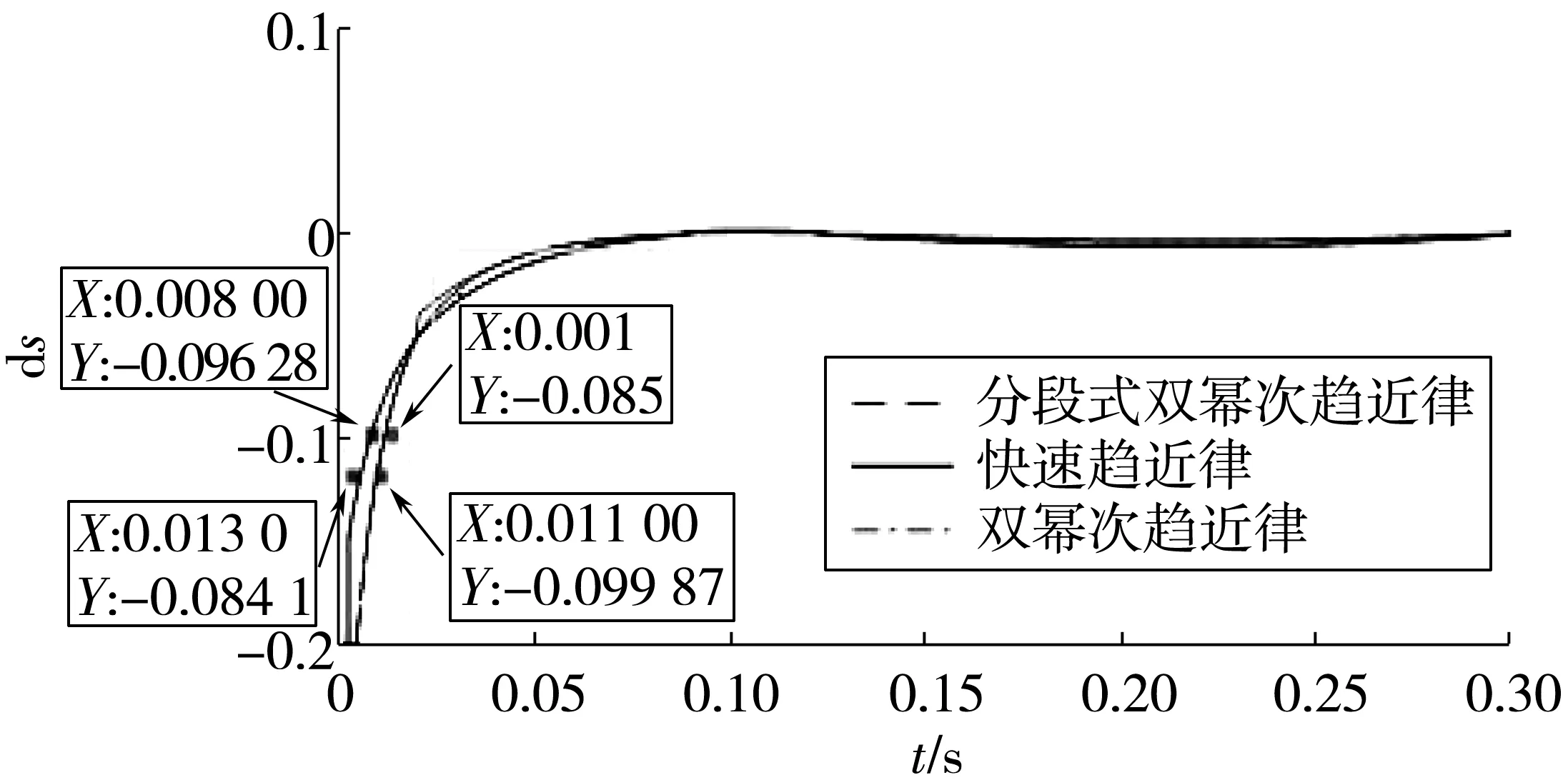
图2 趋近律取点

鉴于分段式双幂次趋近律既能有效削弱抖振，又能提高收敛速度，故选择该分段式双幂次趋近律来设计航向控制器。

2 船舶航向控制数学模型

文献[10]认为：应将船舶看作一个动态系统，建立一阶响应型模型，该模型以舵角为输入，艏向角或艏揺角速度作为系统输出。在实践中发现船舶在航行实际运动中常常呈现非线性，例如不稳定或临界稳定性等情况，因此将一个非线性项添加到一阶线性方程中，如式(18)：

(18)

式中：T为船舶操纵性指数；α为非线性项，由螺旋试验确定；K为船舶旋回性指数。

将式(18)改写为状态空间表达式，如式(19)：

(19)

式中：f(r)=-1/T(α1+α3r3)；g=K/T；d(t)为外部干扰。

实际进行航向控制的舵机大多由电气-液压机构驱动，很难实现阶跃操舵，会有一定延时。因此该舵机伺服系统可由式(20)表示：

(20)

式中：TE为伺服系统时间常数，一般取TE=2.5 s。

3 航向控制器设计

3.1 航向控制器模型

构建航向误差如式(21)：

(21)

为使船舶向能按预期航向航行，因此引入非线性迭代滑动模态[11]，如式(22)：

(22)

迭代滑模法设计将系统控制目标转化为对s2的镇定问题，该系统必须保证s2,s1,e→0，因此系数需要满足k5≥k3。

考虑到船舶模型中d(t)为未知函数，对其估计逼近难度较大，故选择增量反馈来控制舵角的变化率。此处增量反馈选择文中收敛速度更快的分段式双幂次趋近律进行设计，如式(23)：

(23)

为证明该系统稳定性，特此引入李雅普诺夫判据法则，构建新型Lyapunov函数，如式(24)：

(24)

对式(23)进行求导，得式(25)：

(25)

由式(21)可得式(26)：

(26)

(27)

由此可见，该控制系统是渐进稳定的。因此e=ψ-ψd，则航向ψ→ψd，从而控制器可将实际航向跟踪至期望航向。

3.2 分段式双幂次趋近律的参数估计

由文献[12]可知：调节趋近律自身参数也可有效避免抖振。因此选择RBF神经网络，通过仿生物学习来在线估计趋近律参数，进一步削弱抖振。笔者选取转艏角速度和舵角作为RBF神经网络的输入，构成2-8-1结构，其中包含8个隐含层，输出为在线估计的最佳参数。RBF神经网络隐含层输出为非线性函数[13-14]，如式(28)：

(28)

式中：x(t)为输入参数向量；cj(t)为中心向量；‖x(t)-cj(t)‖为两者之间的欧氏距离；bj为高斯基函数的宽度。

神经网络输出如式(29)：

(29)

式中：γ为在线估计的最佳参数；wij为初始权重值，文中wij=1。

定义输出误差指标对输出效果进行评价，如式(30)：

(30)

式中：μ为参数γ的期望值，但其数值为未知量。

用转艏角速度与舵角比值来替代输出误差。文献[15]表明：航行过程中船舶转艏角速度与舵角的比值接近0.035。故误差指标重新定义如式(31)：

(31)

由此神经网络输出便是最佳参数。具体神经网络输出参数如图3。

图3 RBF神经网络输出参数γ值

4 仿真结果

笔者选用大连海事大学教学实习船“育鹏”轮作为研究对象，建立船舶仿真模型，验证控制器效果[16]。该船的基本参数为：船长Loa=189.0 m，船宽B=27.8 m，方形系数Cb=0.72，舵叶面积为38.0 m2，排水量为30 000 t。无量纲化后的船舶模型参数为：K=0.08，T=39.09。

为验证控制器对外界干扰鲁棒性，设定初始状态船舶航向000°。设定所需期望航向为060°。分别在无风作用海况和6级风(风速12 m/s、风向80°)干扰海况下进行仿真比对实验；另一组实验是在RBF神经网络在线调节参数情况下进行。

4.1 无风作用下航向控制

该情况下的航向控制如图4。图4(a)中：这3种趋近律所设计的控制器均能稳定的到达预期航向060°，无超调量，无静态误差，船舶航向变化光滑，符合实际情况。舵角变化情况如图4(b)，快速趋近律控制器收敛速度最快，但其舵角调节高达24°。相比于快速趋近律，分段式双幂次趋近律优势明显，不仅舵角调节度数小，仅为18°；且趋近速度比双幂次趋近律快5%。

图4 航向控制(无风作用)

4.2 风力6级干扰下航向控制

该情况下的航向控制如图5。图5(a)中：在分段式双幂次趋近律固定参数下，面对风力6级(风速12 m/s，风向80°)，该控制器表现出较强的鲁棒性。舵角调节情况如图5(b)，达到预期航向只需调节舵角最大为27°，调节度数明显少于其他两种控制器。最后为使船舶稳定在060°方向，舵角变化范围为+7°～+16°。

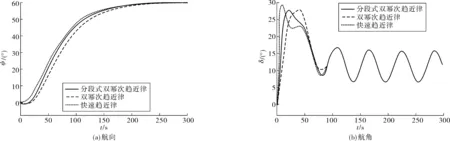
图5 航向控制(有风干扰)

4.3 无风海况RBF在线调节参数航向控制

在线估计参数与固定参数航向(无风)比较如图6(a)。在无风海况下，固定参数设计的分段式双幂次趋近律控制器比RBF在线调节参数控制器所需的上升时间要少，但最终到达稳态的时间二者相差无几，均在180 s左右；再结合图6(b)的神经网络调参的控制器对舵角调节仅为0°～10°，而固定参数为0°～19°，说明明显好于固定参数。

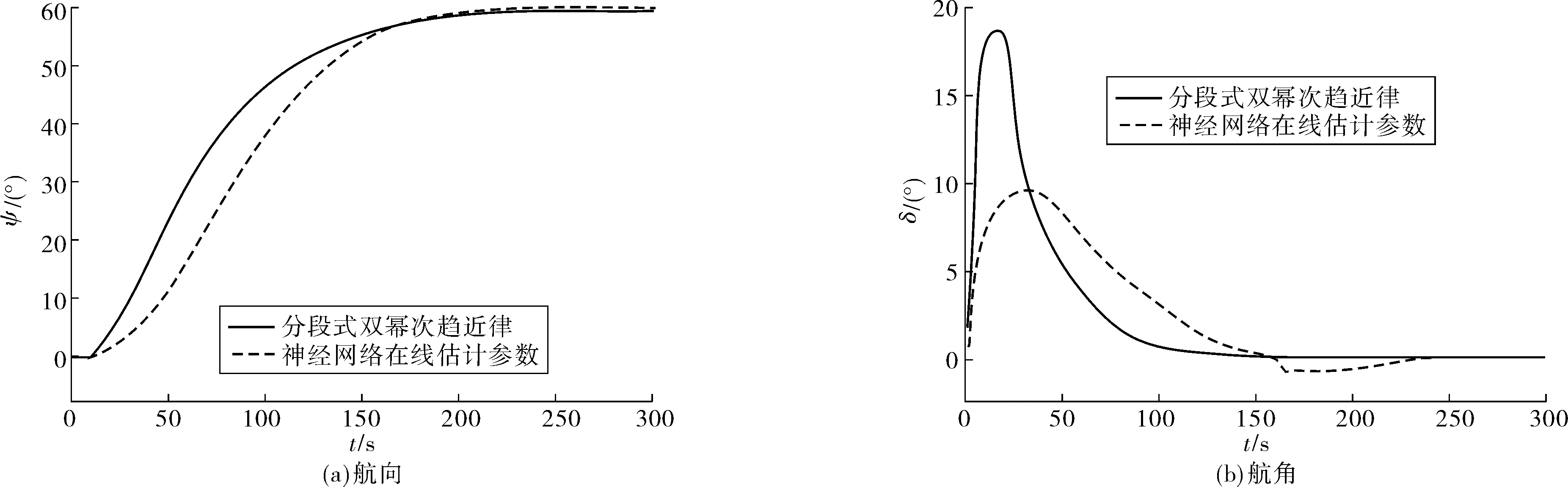
图6 在线估计参数与固定参数比较(无风)

4.4 风力干扰下RBF在线调节参数航向控制

在6级风力(风速12 m/s，风向80°)干扰下，航向调节时间由无干扰下的180 s增加到220 s，如图7(a)。图7(b)为在线估计参数与固定参数舵角(有风作用)比较。图7(b)中：最佳参数选择对趋近律控制器的影响十分明显，对舵角调节仅为0°～24°。在航向到达稳态时，RBF在线调节参数控制器对舵角调节比固定参数少10%。

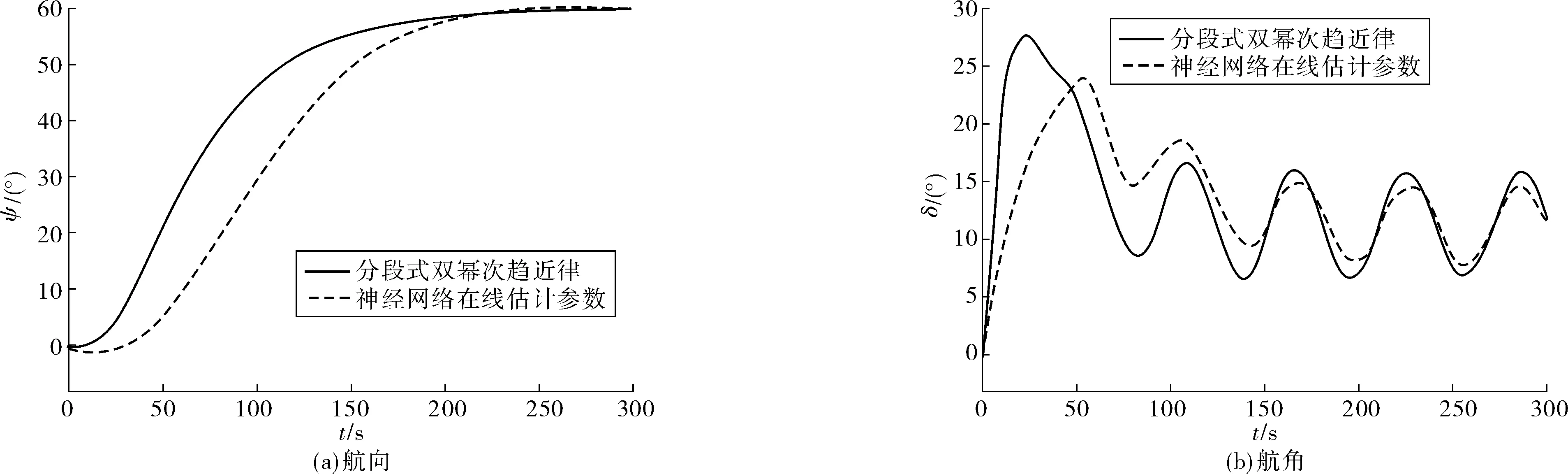
图7 在线估计参数与固定参数比较(有风干扰)

5 结 语

笔者提出的分段式双幂次趋近律，经仿真结果验证能有效减弱滑模变结构控制的抖振，且趋近速度快于快速趋近律。

运用一阶响应型数学模型建立“育鹏”仿真模型，并以此模型为基础设计航向控制器，分别在无风干扰和6级风干扰下进行转舵60°仿真。结果表明：引入分段式双幂次趋近律的控制器比其他两种控制器抗干扰效果更强，最大操舵角度明显减小。考虑到趋近律参数选择亦影响模型抖振和控制效果，引入RBF神经网络在线调节趋近律参数并进行上述两种情况的模拟仿真比较。结果显示：引入RBF神经网络后，虽趋近速率减慢，但最大操舵角度在无风干扰海况下的+17°减小到+10°，6级风干扰海况下的+27°减小到+24°，控制效果明显增强，稳态品质显著提高。