基于改进变权-TOPISIS的锚固边坡失稳风险评估

叶险峰，韩以江，祝敕捷，程 雍

(湘潭大学 土木工程与力学学院，湖南 湘潭 411105)

0 引 言

工程边坡稳定是工程安全施工和运营的重要保障，对其进行失稳风险评估尤为重要。工程边坡多为锚固边坡，其失稳风险受几何尺寸形状、岩土体类型和参数、周边环境、加固结构和施工扰动等多因素综合影响，且各影响因子难以准确度量。监测数据是边坡稳定情况的综合体现，基于多期监测资料的锚固边坡失稳风险评估结果，可以有效反映，工程边坡的稳定情况及动态变化规律[1-3]。在某监测项目状态很危险且常权权重很低时，常权综合结果通常显示为该锚固边坡依然安全，这会和实际情况不符，故笔者引入变权理论。

变权理论由WANG Peizhang率[4]先提出，李洪兴[5]给出了变权理论和状态变权向量的公理化定义，随后又有大批学者对变权理论进行丰富完善[6-9]。变权理论是根据指标状态间均衡水平，确定状态变权向量进而得到变权向量，调整各指标在综合决策中的效能，使得决策在指标组状态均衡的情况下进行[10]。状态变权向量通常由状态变权函数代入变量得到，目前状态变权函数多数是参照组态(指标组状态)失衡程度、决策对象特性构造的[7-12]，因此状态变权函数对组态和决策对象具有针对性。当决策对象包含多组组态失衡度相差较大的状态值时(如多期变形监测数据)，各指标组权重调节所需力度差别也较大，若使用多种状态变权函数，构造难度较大，若使用同种状态变权函数，由于其组态失衡度针对性将可能导致误用，使得变权调节度过大、过小或变权调节度与组态失衡度大小变化方向不一致的情况(如失衡度增大，而调节度减小)。

李德清等[6]提出用状态向量离散度表示指标组组态失衡度，在实际应用中，当状态向量离散度相等时，其组态失衡度并不一定相等。假设在边坡失稳风险评估中，2组监测指标状态值分别为(0.5，0.6，0.7)、(0.8，0.9，1.0)，其离散度相等，设置“激惩平衡区间”相同，一般为区间(0，1)中较为居中位置的区间，显然第2组各状态值与“激惩平衡区间”边界距离较大，其变权调节度会比第1组稍大，则组态失衡度也并不相等。

TOPISIS法(逼近理想解排序法)是按照各评估对象到理想化目标的接近程度对有限评估对象进行优劣排序的方法，已应用于诸多领域[13-16]，在边坡失稳风险评估中也取得了良好效果[17]。

笔者提出一种基于指标状态到“激惩平衡区间”的距离的组态失衡度度量方案，构造一种基于组态失衡度和状态值的混合型状态变权函数模型，并结合TOPISIS法，对锚固边坡进行基于多期监测数据的失稳风险评估。

1 变权原理及常权构建

1.1 变权理论

为避免常权向量在多目标决策问题中因目标组态不均衡而导致不合理综合，文献[4]提出变权理论，文献[5]在其基础上给出了变权向量、状态变权向量等变权公理化定义，如下：

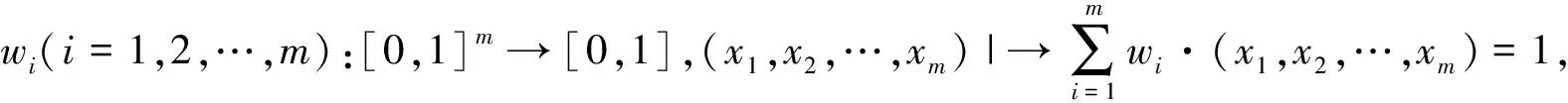
性质2：连续性，即wi(x1,x2,…,xm)关于每一变元连续；

性质3：单调性，即wi(x1,x2,…,xm)关于变元xi递减(惩罚性变权)或递增(激励性变权)。

状态变权向量定义：设Si:[0,1]→[0,1](i=1,2,…,m)，如果S(X)=(s(x1),s(x2),…,s(xm))满足：

性质1：单调性，即对于任意X=(x1,x2,…,xm)∈[0,1]m，当为惩罚变权时，若xi≥xj，则s(xi)≤s(xj)，当为激励变权时，若xi≥xj，则s(xi)≥s(xj)；

性质2：连续性，即Si(x1,x2,…,xm)关于每一变元连续；

(1)

1.2 常权权重向量构建

确定权重方法众多，常用有层次分析法、熵权法及组合赋权法等，笔者是对拥有多层次指标体系的单个评估对象进行风险评估，因此选择较为简单的AHP赋权。鉴于AHP主观性强的缺陷，一致性检验过程复杂，笔者采用“三角模糊数”改进的层次分析法确定指标常权权重[18]，步骤如下：

1)一级指标常权权重向量W*构建。首先构造三角模糊综合判断矩阵，并将其转换为模糊判断因子矩阵，再在其基础上计算得到调整矩阵，然后对调整矩阵进行相容变换，最后计算出一级指标常权权重向量W*。

2)指标常权权重向量Wo构建

二级指标的计算如式(2)：

(2)

式中：i=1，2，…，k，k为一级指标个数；j=1,2，…，λ，j为某一级指标下二级指标个数；δ为某二级指标常权权重占该一级指标常权权重的比例系数，按照所在该一级指标下二级指标间的重要程度确定。

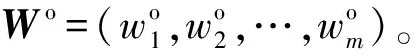
2 基于变权-TOPISIS法的评估模型

2.1 绝对理想方案标准化判断矩阵

TOPISIS法是通过在样本方案集内部寻找理想解，并计算各方案与理想解的相对贴进度，然后进行优劣排序的方法[16]。因此该方法多用于样本方案集内部排序，因样本方案集决定的理想解通常只对样本方案集有效，对其它样本方案不一定成立。指标评估等级标准阈值第一列和最后一列客观上能代表评价目标的最优和最劣方案，笔者将其固定作为评估对象的绝对理想方案。

设包括指标评估标准等级阈值方案在内，共有n个决策方案，每个方案有m个指标，指标bij(其中i=1，2，…，m；j=1，2，…，n)为第j个方案的第i个评估指标。则n个方案构成的特征矩阵B如式(3)：

(3)

其中，第1列为负理想方案，第2～5列为指标评级等级标准阈值方案，第n列为正理想方案。

方案指标分为效益型(值越大越好)和成本型(值越小越好)两类，为统一量纲，对判断矩阵进行标准化处理，得到标准化判断矩阵C=(cij)m×n，即为评估值判断矩阵，计算公式如式(4)、(5)：

对效益型指标：

(4)

对成本型指标：

(5)

正、负理想方案标准化即为绝对理想解，如式(6)：

(6)

2.2 组态失衡度

实际应用中，由于激惩平衡区间的划分，导致状态值离散度无法准确体现组态失衡度，笔者提出一种基于状态值到激惩平衡区间边界的距离的组态失衡度度量方案。

设qξ、qζ分别为低于惩罚水平、高于激励水平值的指标状态值，(α，β)为评估对象指标“激惩平衡区间”，τ为“激惩幅度比”(激励与惩罚幅度的比值)，l、h分别为权重受惩罚、激励的指标个数，指标组组态失衡度R计算如式(7)：

(7)

当指标状态值不同时，式(7)中指标组组态到“激惩平衡区间”边界距离越大，R值越大，其组态失衡程度越大，各指标权重所需调节力度越大，和实际情况相符；当指标状态值相同时，无论R值大小，状态变权函数值相等，各指标权重所需调节力度相等，等效于调节度为0，和实际情况亦相符。

2.3 状态变权函数的构造及变权权重

针对已有状态变权函数，在决策对象包含多组组态失衡度相差较大的状态值组，这一情况下适用性较低的问题，笔者构造一种包含组态失衡度的混合型状态变权函数，如式(8)：

(8)

式中：R为指标组组态失衡度；xi为指标i的状态值；m为指标组指标个数；τ为“激惩幅度比”；α、β分别为惩罚和激励的指标状态临界值，(0，α)为惩罚区，[α，β]为“激惩平衡区间”，(β，1]为激励区，其中α、β、τ由专家建议确定。

经验证，式(8)满足文献[5]给出的变权公理中的各性质，同时满足提升对极端指标关注度、激励幅度小于惩罚幅度、不能脱离常权限制等要求[11]。

最后，结合式(2)～式(7)计算常权向量Wo及状态变权向量S(X)，代入公式(1)，可得最终变权向量W(X)。

2.4 计算各方案的评估结果

2.4.1 加权标准化决策矩阵

对标准化判断矩阵C=(cij)m×n中第μ个方案标准化数据和理想解赋权(η=2，3，…，n-1)，理想方案标准化后为标准化决策矩阵的第1列和最后一列，得到判断矩阵Tμ：

(9)

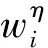
2.4.2 各方案到绝对理想方案的相对贴近度

相对贴近度可以用欧式距离来度量，表示为E，第个η方案的相对贴近度Eη：

(10)

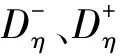
(11)

在边坡失稳风险概率评估中，Eη即为第η个方案的失稳风险概率值。

3 案例应用及分析

笔者以灯盏坞隧道进口端洞顶仰坡为例，进行锚固边坡失稳风险评估。该边坡地质构造复杂，且有仰坡顺层，整体地下水不发育，主要加固措施为锚固桩和锚索框架梁。为确保工程施工和运营安全，从位移和应力两方面，对边坡进行框架梁上表面的坡顶表面位移、深部位移、锚固桩桩顶水平位移、锚索框架梁锚索拉力、框架梁与土接触面压力、桩侧土压力等跟踪监测，频率为5 d/次，并进行边坡失稳风险评估，如图1。

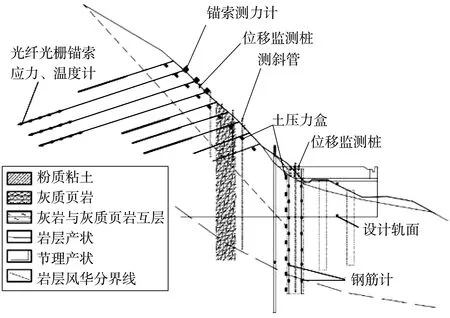
图1 边坡监测元件分布剖面

3.1 锚固边坡失稳风险性评估体系

在遵循典型性、独立性、层次性、可靠性、可量化等指标选取的原则之下，选取指标如表1。由于该锚固边坡地下水不发育，对稳定性影响较小，同时由于该项目没有地表裂缝监测项，地表裂缝被施工残渣及溜沙遮挡，单靠人工巡视无法确定其准确情况，此处未选取地下水位指标和地表裂缝指标。

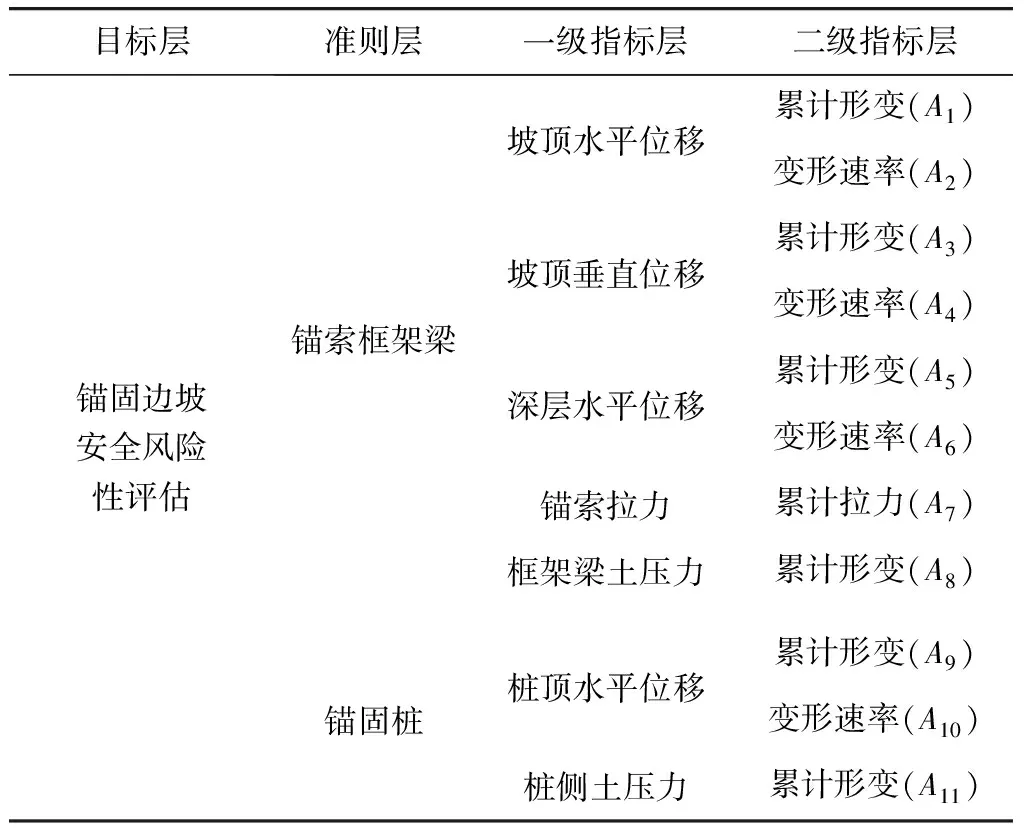
表1 风险评估指标体系

3.2 各监测项目风险等级

笔者将边坡失稳风险划分为5个等级，对应的评语集V={Ⅰ级,Ⅱ级,Ⅲ级,Ⅳ级,Ⅴ级}={安全状态,跟踪状态,预警状态,报警状态,危险状态}，则评判指标i也划分为5个等级标准区间，并以各个监测项目规范或设计文件规定的各项形变设计允许值为基准，考虑到设计较为保守，以设计允许值的60%、90%、110%、120%、125%对形变累计指标进行分级，以设计允许值的50%、80%、100%、110%、115%对速率指标进行分级[19-20]，具体如表2。

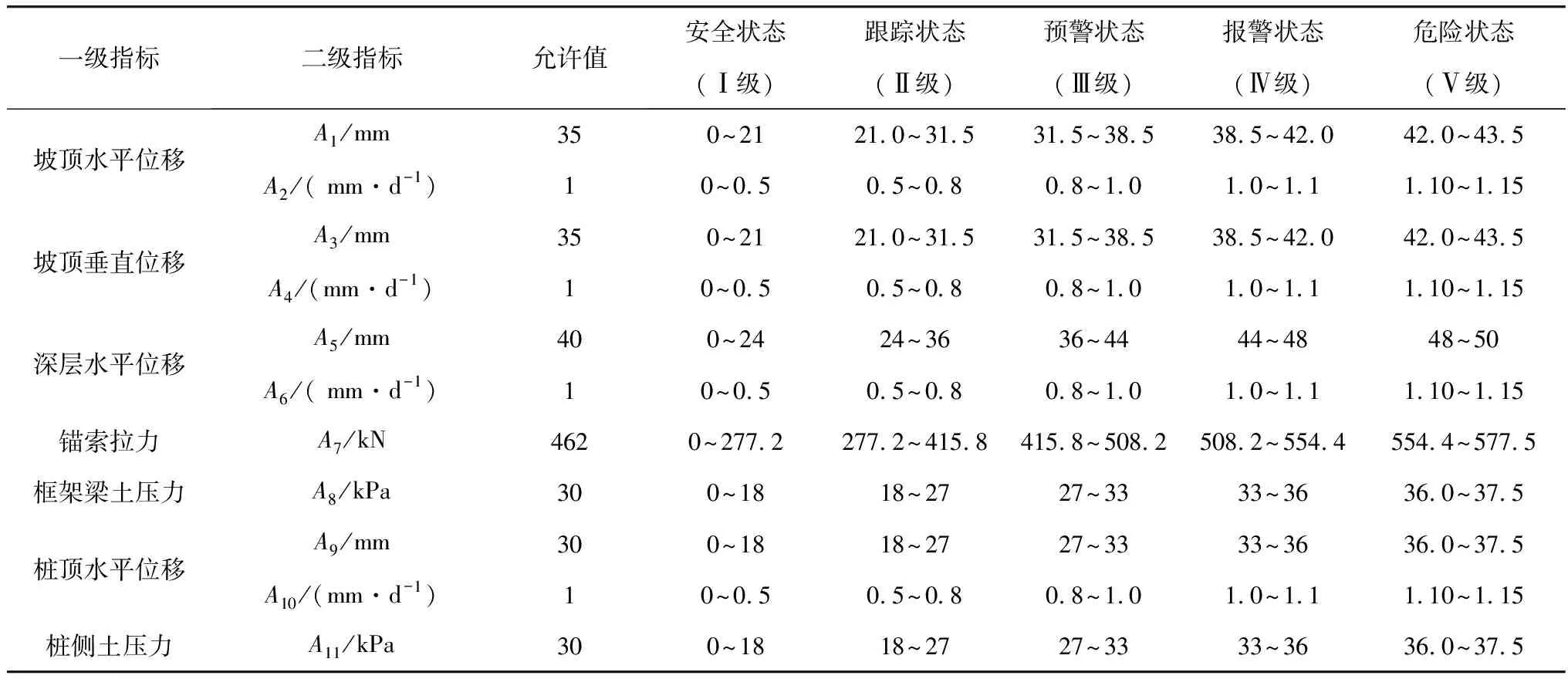
表2 指标评估等级标准划分

3.3 指标变形监测数据

笔者以累计形变量最大监测点量测数据作为指标数据。该隧道进口2018年4月27日上台阶开挖，2018年5月31日隧道上台阶约开挖30 m，2018年6月30日隧道开挖约65 m，2018年7月31日隧道开挖约80 m，2018年7月5日完成明洞仰拱、洞口管棚支护，此过程中，隧道开挖对边坡的扰动从逐渐增大到逐渐降低到可忽略，且该边坡受其它因素影响较小，因此5、6、7月是该边坡失稳风险高峰期，对其进行评估则可以把握该边坡失稳风险变化情况及未来边坡稳定情况，对该3个月监测数据平均每半个月进行一次评估，各指标监测数据数值如表3。

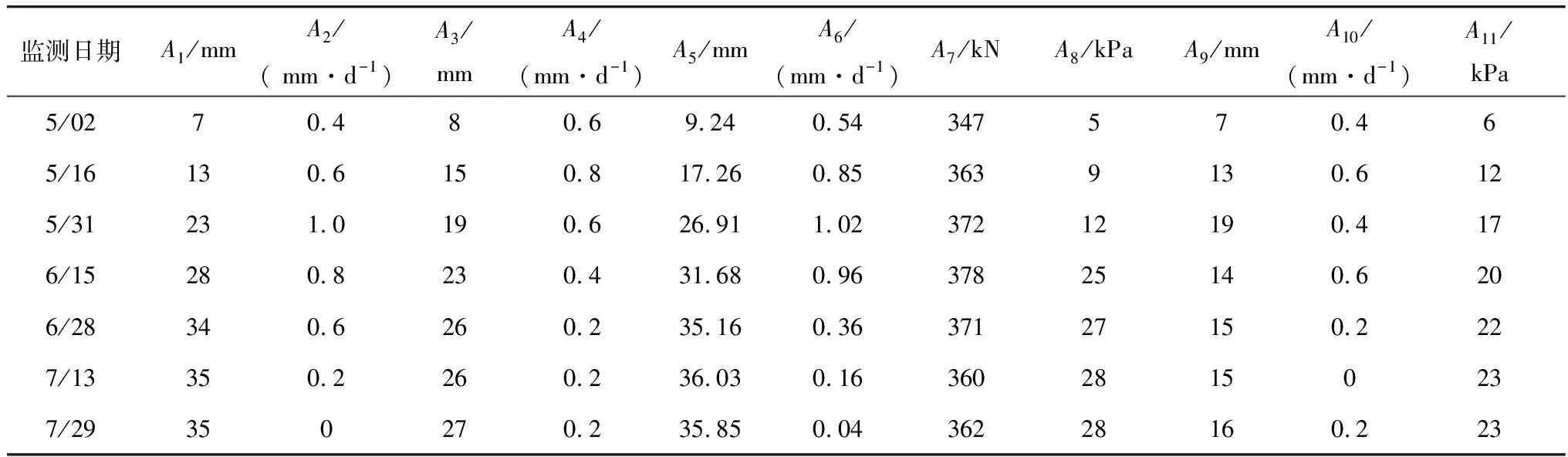
表3 各指标各期监测数值

3.4 锚固边坡失稳风险评估

1)常权权重的确定

笔者邀请到5位专家分别运用“1～9标度法”对各指标权重三角模糊打分，计算得到一级常权权重：W*=(0.219,0.148,0.194,0.088,0.063,0.165,0.123)。由于采用最大变形速率比采用最大变形值来判断评估变形体的失稳风险更加准确[21]，故确定W累计形变∶W变形速率=2∶3，即δ1=0.4，δ2=0.6，最终得到常权权重，如表4。

2)变权权重的确定

首先由指标评估等级标准划分阈值和各期指标监测数值构造初始判断矩阵，并进行标准化，得到指标监测值标准化判断矩阵C，即指标状态值；经状态变权模型，计算得到各评估方案样本的组态失衡度R及变权向量，其中α=0.3，β=0.7，τ=0.8，具体结果见表4。为方便对比分析，增加常权权重，

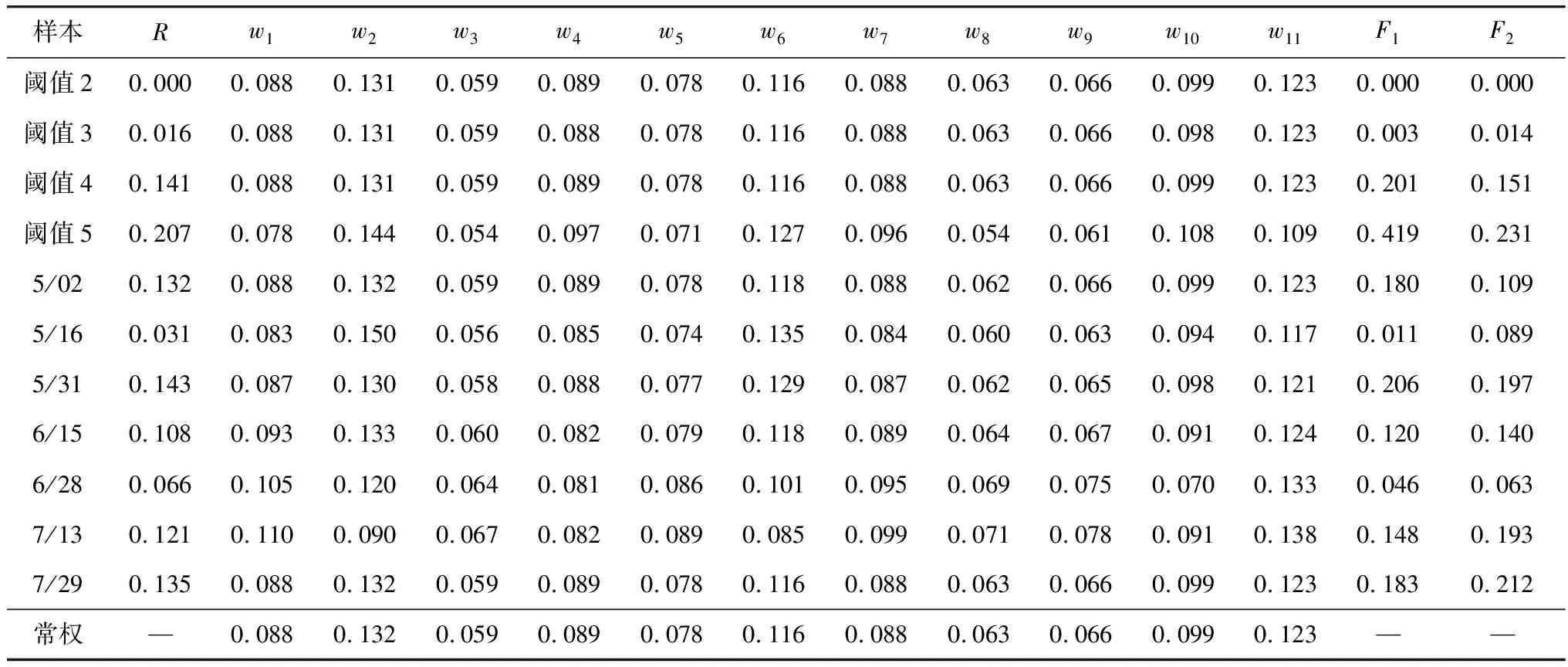
表4 各方案样本变权权重

参考文献[6]中变权调节度的算法,以状态变权函数与1的偏差绝对值的均值之和除以状态值在“激励平衡区间”之外的指标个数得到变权调节度F1。

3)评估结果计算

由矩阵C和表4中各方案变权向量，得到各方案贴近度E，即边坡失稳风险概率值。为验证笔者评估模型的优越性，增加常权、文献[11]中具有代表性的混合型状态变权函数与TOPISIS法结合的评估模型作对比，其中参数取值与笔者相同，变权调节度F2见表4，变权评估结果见表5。

表5 各评估模型评估结果

3.5 结果分析

1)状态变权结果分析

部分监测和阈值方案各指标变权权重与常权权重对比情况，如图2。由图2可知，阈值样本各指标变权权重与常权基本相等，而监测样本各指标变权权重与常权偏差较为明显。笔者各指标阈值按各设计允许值等比设置，且各对应等级间比例较为接近，其组态较为均衡，各阈值方案权重基本无需调整，监测数据样本各指标状态相差较大，需进行权重调整，而图2中阈值样本权重变化情况与理论相符，这证明笔者变权模型具有合理性。

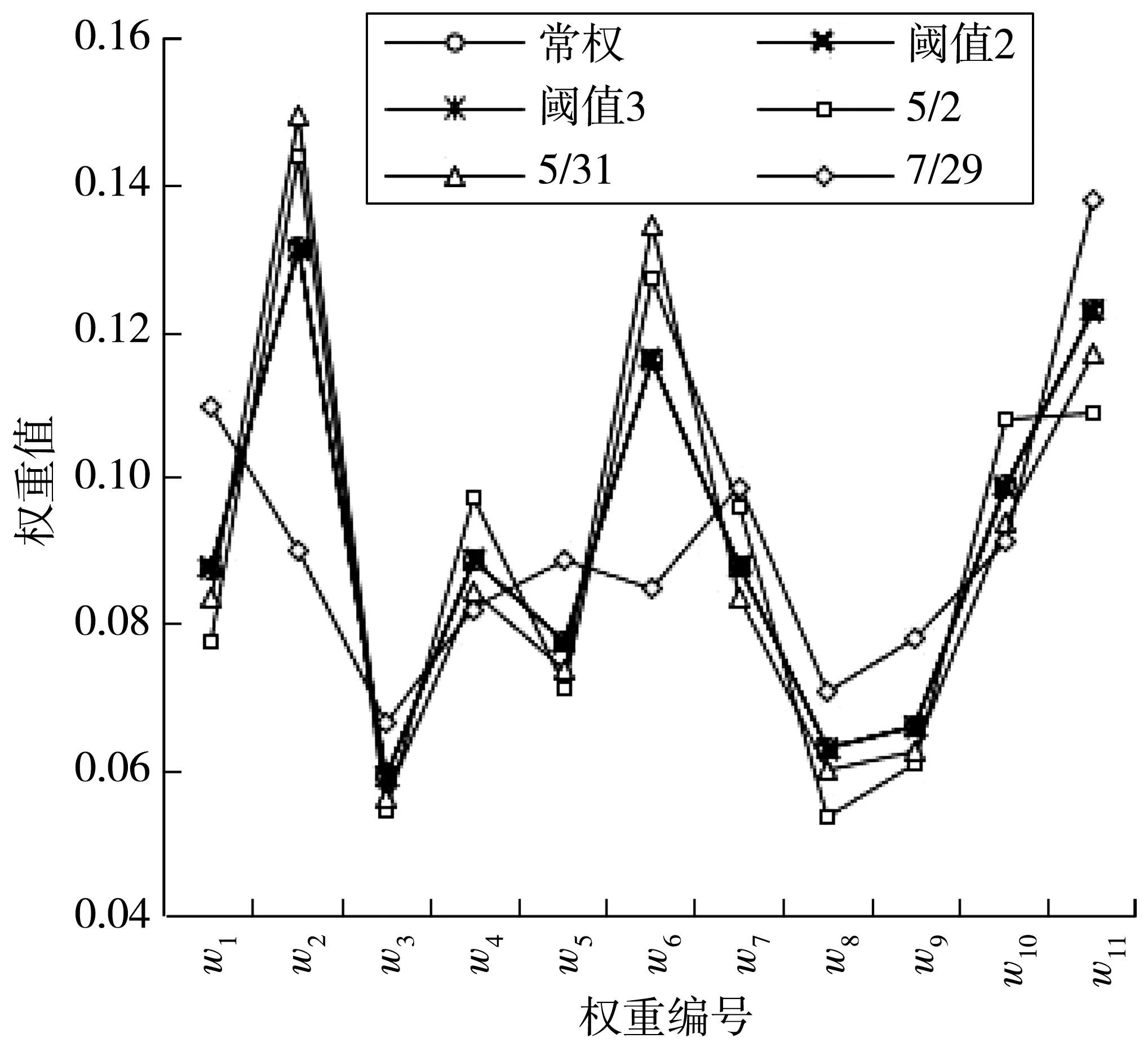
图2 变权与常权权重对比

将表4中各评价等级阈值方案及各期监测数据方案对应的两种变权函数的变权调节度F1、F2,与组态失衡度R绘制成图3。由图3可见，各方案的指标组组态失衡度大小顺序为“阈值2<阈值3<5/16<6/28<6/15<7/13<5/02<7/29<阈值4<5/31<阈值5”，按文献[12]中状态变权函数模型求得的变权调节度大小顺序为“阈值2<阈值3<6/28<5/16<5/02<6/15<阈值4<7/13<5/31<7/29<阈值5”，笔者中状态变权函数模型求得的变权调节度大小顺序为“阈值2<阈值3< 5/16<6/28<6/15<7/13<5/02<7/29<阈值4<5/31<阈值5”。由文献[4]～[9]可知，指标组组态失衡程度越大，权重所需调节度越大。按文献[11]中的状态变权函数得到变权调节度并未随组态失衡度增大而严格增大，笔者包含组态失衡度的状态变权函数得到的状态变权向量严格满足这一要求，这证明笔者的变权模型更优越。

图3 状态变权调节度分析

2)案例锚固边坡失稳风险分析

对比3种评估模型综合评估结果，如图4。在风险等级方面，3者得到的等级阈值完全一致，其中7月13日和7月29日变权评估模型得到的风险等级比常权高一级；在风险评估数值方面，变权方模型比常权评估模型得到的各期监测数据的失稳风险值整体偏大，3者评估结果值变化趋势相同，其中2种变权评估模型得到的失稳风险峰值都较常权评估模型提前了5天左右，且2种变权评估方案得到的风险值和风险等级都具有高度的相似性。综上可知，笔者变权模型科学合理，同时在锚固边坡失稳风险评估中，变权评估模型优于常权评估模型。

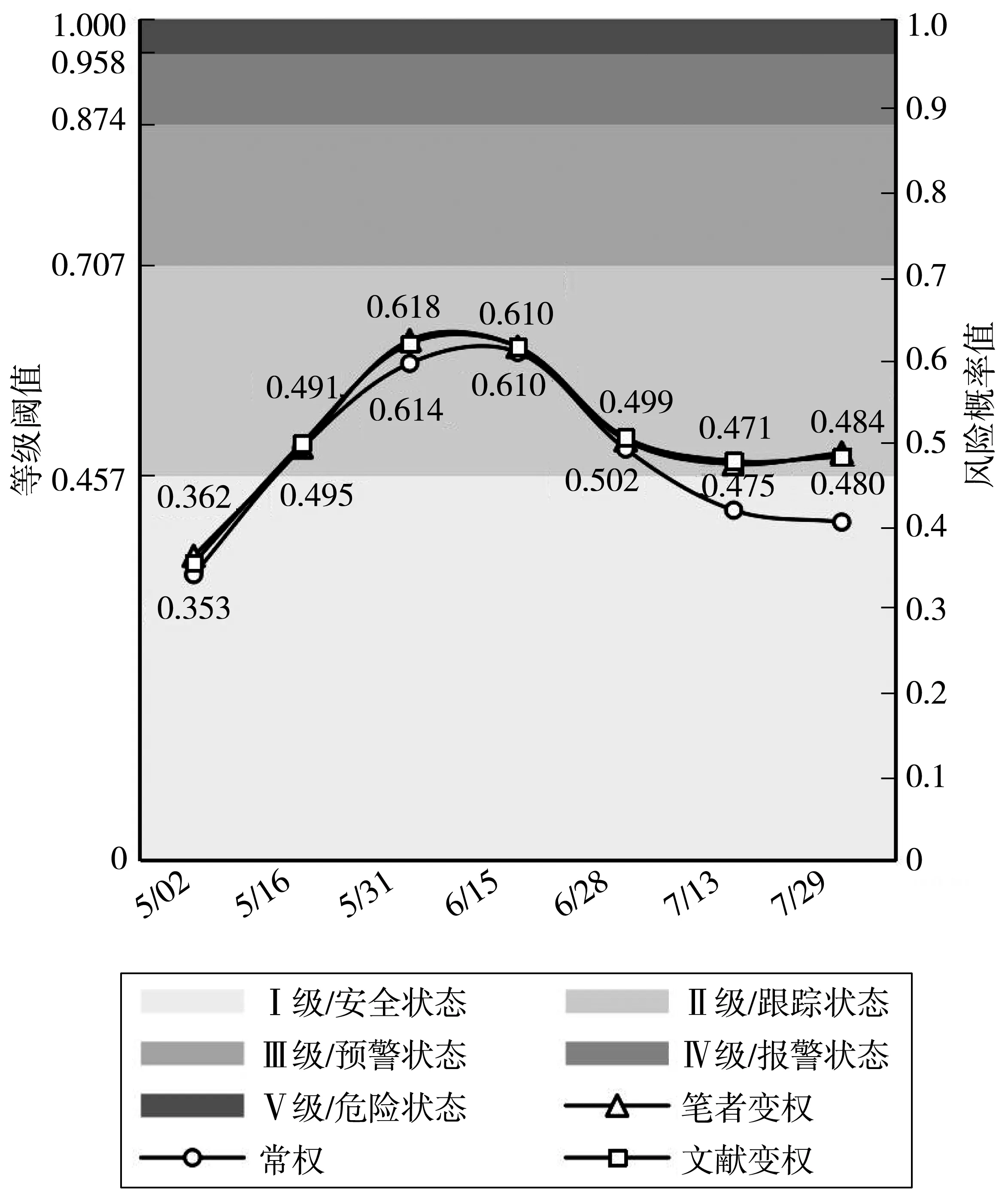
图4 各评估模型结果对比

如图4，笔者变权模型得到的锚固边坡失稳风险峰值及失稳风险较小值都比文献变权评估模型得到的结果大，失稳风险程度一般的结果相对较小。在混合变权模型在风险偏好类的评估中，权重调整通常会使得评估结果更倾向于负面，因为它将状态较为恶劣的指标权重调大，将状态较优的指标权重调小，以常权评估结果作为参照，权重调节力度越大评价结果增大越明显。结合图3可知，笔者的变权模型在组态失衡程度较大时，权重调整力度较大，组态失衡程度较小时，权重调整力度较小，而2种变权评估模型设置的参数大小相同，这说明笔者变权模型，相较对比模型对状态较为极端的指标敏感性较高，较均衡的状态值敏感性较低，这更符合变权混合变权模型的要求“提升对极端指标的关注度”。因此，在锚固边坡的失稳风险评估中，笔者变权模型优于对比变权模型。

分析笔者变权评估模型综合评估结果可知，该案例锚固边坡失稳风险概率值从5月2日至6月10日左右不断增大，从6月10日左右至7月10日左右，不断减小，从7月10日至7月29日缓慢变化。5月2日至5月13日左右，该锚固边坡失稳风险等级为“Ⅰ级”，风险状态为“安全状态”。5月13日左右至7月29日，该锚固边坡失稳风险等级为“Ⅱ级”，风险状态为“跟踪状态”。

结合工程施工进展分析，该隧道口锚固边坡于2018年4月27日开挖，开挖之初，由于洞口管棚和明洞仰拱支护施工未完成，加之开挖施工扰动，边坡应力释放，进行表生改造和应力场调整，应力和位移变形加快，使得边坡失稳风险概率升高；6月初，开挖超过30m，超出了坡面里程范围，随着边坡下方施工的继续进行，其施工扰动逐渐减小，边坡应力场逐渐转化为自重应力场为主，边坡应力和位移减缓，其失稳风险概率降低；7月10日，随着洞口管棚、明洞仰拱支护的完成和施工开挖深入，支护达到饱和状态，坡体下滑力和支撑力达到平衡，锚固边坡整体上逐渐趋于稳定。综上可知，所得评估结果与该锚固边坡实际情况完全相符，证明笔者变权评估模型适用于锚固边坡失稳风险评估。由于该锚固边坡今后所受工程扰动较小，且处于地震低发地带，地下水不发育，其负面影响因素较少，加固设施完备，故可判定之后该锚固边坡失稳风险等级将不高于“Ⅱ级”，即“跟踪状态”，较为安全。

4 结 论

1)在实际应用中，基于指标状态到“激惩平衡区间”的距离的组态失衡度能较好的体现指标组态失衡情况。

2)包含组态失衡度的状态变权函数模型，在决策评估对象包含多组组态失衡度相差较大的状态值时，得到的变权调节度依然满足“指标组状态失衡程度越大，变权调节度越大”的要求，即适用性更高，同时其对优势和劣势状态敏感度更高，对较平衡的状态敏感度更低，效果更好。

3)笔者变权理论与TOPISIS法结合的评估模型能较好的适用于锚固边坡失稳风险评估。

4)2种变权与常权评估结果对比，验证了变权评估模型对优势和劣势状态指标更敏感，优于常权评估模型。