基于混合有序Probit模型的货车翻车驾驶员伤害程度研究

2021-03-05李俊辉汤左淦

重庆交通大学学报(自然科学版) 2021年2期

李俊辉，汤左淦

(1.广东交通职业技术学院轨道交通学院，广东广州 510650；2.深圳市城市交通规划设计研究中心股份有限公司，广东深圳 518057)

0 引言

据美国公路交通安全管理局2018年公布的数据显示，美国全国翻车事故比例不足2%，而因翻车事故造成的死亡人数占比却高达33%[1]。与此同时，在翻车事故中，货车驾驶员遭受死伤的风险远高于普通乘用车驾驶员，是翻车事故中典型的高死伤率群体。据美国官方公布的数据显示，涉及货车的死亡翻车事故频率是涉及小汽车的死亡翻车事故频率的2倍[2]。因此，研究货车翻车驾驶员伤害程度的影响因素尤为必要。

国内外已有部分学者开展了关于翻车事故或驾驶员伤害程度估计方面的研究。如2018年，胡骥等[3]第一次从统计学的角度分析翻车事故伤害程度，其建立的Ordinal Logistic模型结果显示，系安全带、干燥的路面和直线的道路线形能够有效地降低翻车事故的严重性。肖烽等[4]通过吸取Logistic回归模型和朴素贝叶斯算法的优点提出了一种新的两阶段统计模型，并用翻车事故数据验证了新模型的有效性。为分析安全因素对汽车和摩托车翻车事故伤害程度影响的区别，基于美国Michigan州长达10年的翻车历史数据，张渤[5]建立了序次logit模型组，实证结果表明，影响因素差异较大，汽车与机动车翻车事故应分别建模研究，不适合集计在一个模型中。基于美国New Mexico州两年的数据，Q.WU等[6]建立了mixed logit(ML)模型，模型结果首次发现了同性别的驾驶员对翻车事故伤害程度的影响同样具有差异性。A.J.ANARKOOLI等[7]在前人的基础上，首次将random-effects generalized ordered Probit(RGOP)模型引入至翻车事故伤害程度研究中，并与ML模型做对比，实证结果表明，RGOP模型优于ML模型，并发现路肩宽度、接入点数量等多个因素与伤害程度显著相关。同时，也有部分学者利用机器学习模型预测翻车事故严重性。例如C.CHEN等[8]建立翻车事故的支撑向量机模型，识别出是否系安全带和驾驶员人口学特征等8个显著因素。

此外，在涉及货车的事故伤害程度分析方面，不少国内外学者开展了相关的研究并取得了较多的成果。X.Y.ZHU等[9]通过构建有序Probit模型分析事故特征、车辆特征以及驾驶员特征对重型货车事故伤害程度的影响，研究发现一系列驾驶行为因素如驾驶员的精神状态、酒后驾驶以及驾驶员情绪与事故伤害程度相关；J.D.LEMP等[10]利用异方差有序Probit模型分析环境、驾驶员以及车辆因素对重型货车事故伤害程度的影响，研究发现货车拖车的个数、货车的长度以及货车的额定载重与事故伤害程度呈正相关；2013年，X.QIN等[11]开创性的采用多项式logit模型、部分优势比模型以及ML模型研究大货车事故伤害程度，研究发现3个模型的参数估计非常接近，但是拟合优度和预测精度结果均表明部分优势比模型优于多项式logit模型和ML模型；D.M.CERWICK等[12]通过构建潜类别logit与ML的大货车事故伤害模型，研究发现一系列时空因素、道路、驾驶员以及环境因素在两个模型中均与事故伤害程度显著相关，并且潜类别logit模型具有更高的拟合优度。

通过梳理和总结相关的研究成果可知，前人对全车型的翻车事故和纯货车事故进行了较多的研究，但是对货车翻车事故伤害程度的研究却不够深入，主要体现在以下3个方面：①大部分针对翻车事故伤害程度研究将不同车型集聚在一个模型进行研究，但不同车型的轴重、重心等相差较大，集聚在一起研究可能导致有偏的模型参数估计；②针对翻车事故程度以及货车事故伤害程度的研究较多，但是对涉及货车这种特定车型的翻车事故的研究鲜有涉猎；③前人采用了较多的离散选择模型分析事故的严重性，但是鲜有文献同时考虑到事故伤害程度的有序特性(如将事故伤害程度划分为未受伤、轻伤、重伤、死亡)和安全因素对事故伤害程度的差异性影响(异质性)。综上所述，笔者将采用同时考虑驾驶员伤害程度的有序特性和异质性的混合有序Probit模型分析货车翻车驾驶员伤害程度的影响因素，以深入了解各安全因素对货车翻车驾驶员伤害程度的影响机理，为交通管理部门提升交通安全水平，降低货车翻车事故的严重性提供支撑。

1 数据概述

考虑到目前国内交通事故数据采集标准不完备、较多事故字段存在空白或错漏等质量不高，难以适应深度成因分析等技术分析工作等问题，笔者采用美国Texas州的交通事故数据用以实证分析。为了减少因道路环境和城市发展变化带来的估计偏差，笔者仅选取一年(2016年)的历史数据用以研究。美国Texas州的历史事故数据是开放获取的，可在Texas州交通厅的官方网站申请获取(https://cris.txdot.gov)。

考虑到货车翻车单车事故(仅涉及一辆货车的翻车事故)与货车翻车多车事故的发生机理相差甚大，并且翻车货车多车事故的发生比例较低，故笔者只考虑仅涉及一辆货车的翻车事故。在正式分析数据前有必要对原始事故数据进行数据清洗，包括剔除不合理(如驾驶员年龄过小)、干扰的数据(非货车事故)和不完整的单条事故记录。经过数据预处理，最终保留3 476起翻车货车事故作为研究对象，选取驾驶员、车辆、道路以及环境特征共24个安全因素为自变量，见表1。因变量为驾驶员伤害程度。美国Texas州的事故采集标准将驾驶员伤害程度根据严重性从高到低划分为5个水平，依次为死亡、失能伤害、非失能伤害、可能受伤、未受伤。由于死亡和失能伤害的比例非常低，故将这两个类别合并为失能性伤害或死亡。失能伤害或死亡、非失能伤害、可能受伤以及未受伤的比例分别为8.52%、19.94%、15.33%以及56.21%。

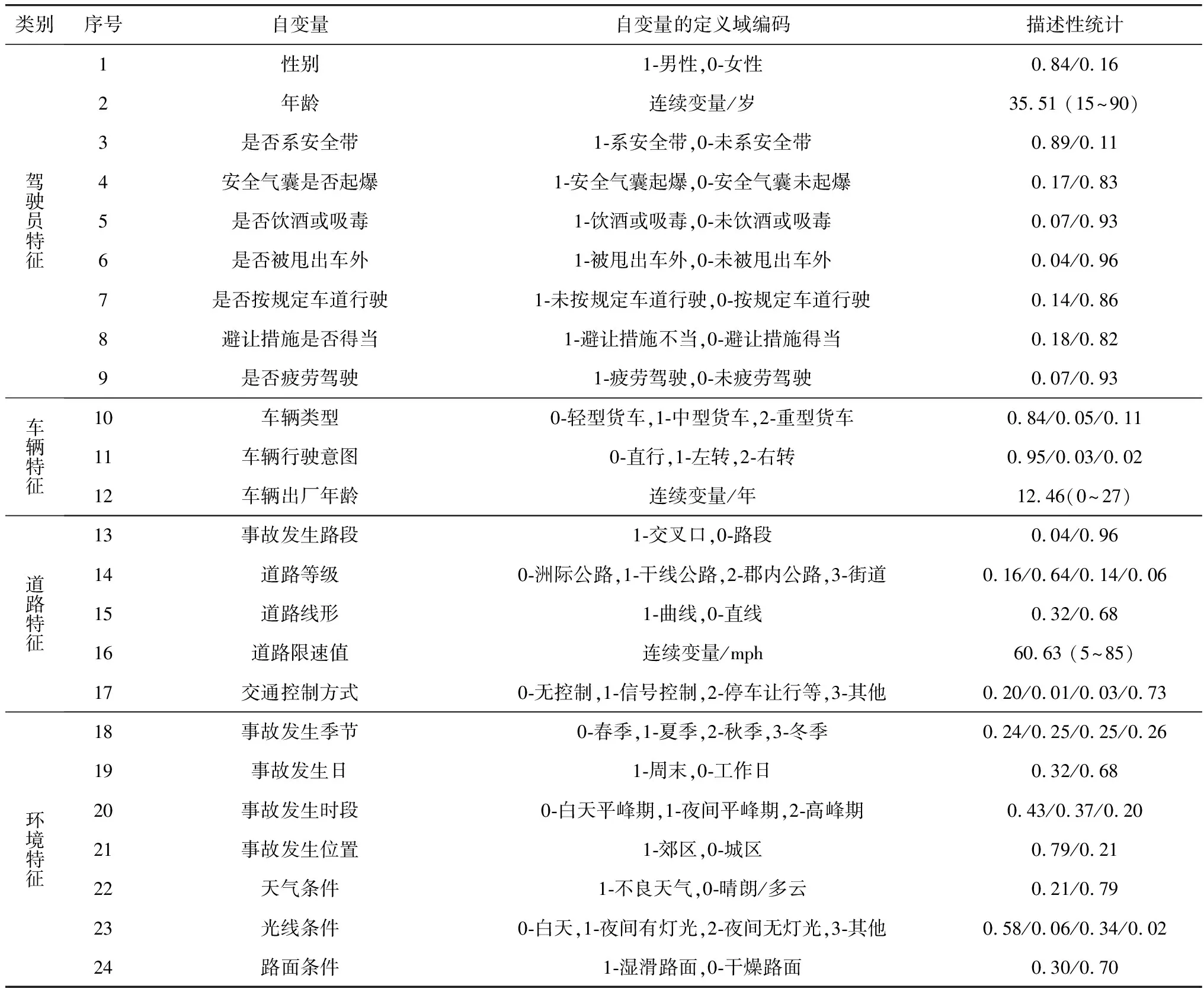
表1 自变量的定义与描述性统计

2 研究方法

2.1 混合有序Probit模型

笔者拟采用混合有序Probit模型分析货车翻车驾驶员伤害程度。为建立混合有序Probit模型，先引入一个线性的伤害倾向性函数[13]：

Si=βXi+εi

(1)

式中：Si为对应于驾驶员i的伤害倾向潜变量；Xi为自变量的集合(驾驶员年龄、是否系安全带、安全气囊是否起爆等)；β为对应于Xi的参数估计；εi为误差项。当εi独立同分布并且服从标准正态分布，则可推导出传统的有序Probit模型的表达式。驾驶员的伤害程度Yi可通过有序Probit模型的Si变量映射得到式(2)：

(2)

式中：μj为有序Probit模型的阈值参数；μ0被标准化为0。基于此，在有序Probit模型中，驾驶员i遭受伤害程度j的概率可以表示为：

(3)

式中：F(·)为εi的累积概率函数。有序Probit模型的参数被预先假定为不随样本个体而变的固定参数，故而不能捕捉样本个体的异质性。通过放松有序Probit模型中的固定参数假设，使β服从某种随机分布，则可导出混合有序Probit模型。混合有序Probit模型中β的第k个分量βk定义为：

βk=μk+σkνik

(4)

式中：μk和σk分别为βk的均值和标准差；νik为第i个样本的不可观测随机效应。在前人的研究中，νik经常被设定为正态分布[14,15]，因此笔者选择正态分布作为待估参数的分布形式。混合有序Probit模型与ML模型类似，其表达式存在高维积分，无法通过数学解析法求出精确解，一般采用最大似然模拟仿真进行参数估计。前人在使用计算机模拟仿真求解时发现，Halton抽样法比随机抽样法的求解效率更高[13,16]，因此笔者采用Halton抽样法求解。

2.2 边际效应计算

混合有序Probit模型中的参数估计只有其正负符号表示正相关和负相关，其实际参数估计值没有意义，只能用以定性分析。为定量分析各变量对驾驶员伤害的影响，在估计模型的参数后，计算自变量对驾驶员伤害程度的边际效应。对于连续自变量，边际效应的计算公式为：

(5)

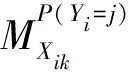
(6)

式(6)衡量当Xik从0变化到1所引起驾驶员伤害程度j的概率变化。不管是0-1变量还是连续变量，对于每一个事故样本均有一个边际效用值，因而笔者采用所有事故样本的平均边际效用值表示自变量对驾驶员伤害程度的定量影响。

3 实证分析

3.1 参数估计

以3 476起货车翻车事故为研究对象，选取人、车、路、环境共24个候选自变量，构建混合有序Probit模型之前，先构建有序Probit模型。将表1中的24个自变量纳入到有序Probit模型中，取显著性水平为0.05，采用混合逐步回归法确定显著变量。通过计算发现男性、年龄、是否系安全带、安全气囊是否起爆、是否饮酒或吸毒、是否被甩出车外、是否按规定车道行驶、重型货车、车辆右转、不良天气、道路限速值以及车辆出厂年龄共12个变量(包含虚拟自变量)与驾驶员伤害程度显著相关。

基于有序Probit模型的参数估计结果，将有序Probit模型中的12个显著自变量作为混合有序Probit模型的候选自变量。同样地，取显著性水平为0.05，将所有候选自变量的参数假定为服从正态分布。模型求解时采用Halton抽样法，抽样次数取为200。混合有序Probit模型的参数估计结果显示，有序Probit模型中的12个显著自变量在混合有序Probit模型中均显著，并且男性、饮酒或吸毒、被甩出车外以及车辆右转变量的参数估计为随机参数。有序Probit模型与混合有序Probit模型的参数估计结果如表2。对比2个模型的McFadden伪R2可以发现，混合有序Probit模型的拟合优度高于有序Probit模型。因此，笔者只计算混合有序Probit模型中各自变量的边际效应，并只分析混合有序Probit模型中的结果。

表2 有序Probit模型与混合有序Probit模型的参数估计

3.2 结果分析

3.2.1 男性驾驶员

男性驾驶员变量的参数服从N(-0.403, 0.3932)的正态分布，表明相比于女性驾驶员，84.85%的男性驾驶员更不容易受较重的伤害，而15.15%的男性驾驶员更容易受到严重的伤害。这主要是因为同性别间驾驶员的其他人口学特征差异导致的异质性结果[17]。边际效应结果显示，总体而言，男性驾驶员遭受非失能伤害、失能伤害或死亡的概率分别降低8.91%、5.11%。前人的研究结果发现，女性驾驶员对突发风险的处理能力明显弱于男性[18]。针对此性别差异，可以考虑在驾考培训时，专门设置应对突发事件的模拟驾驶课程，尽可能从源头上防控风险，避免女性在驾驶货车的途中发生翻车事件。

3.2.2 驾驶员年龄

边际效应结果显示，驾驶员的年龄每增加一岁，遭受非失能伤害和失能伤害或死亡的概率分别增加0.08%和0.04%。这说明了随着年龄的增加，驾驶员的反应能力以及对车辆的操控能力均有所下降，从而更容易发生严重的事故。对于货车这种营运车辆，交通管理部门可能需要适当降低从事货物运输的年龄上限。

3.2.3 系安全带

模型结果表明，系安全带能够最大程度地避免货车驾驶员遭受严重的事故伤害。具体而言，系安全带后，驾驶员遭受失能伤害或死亡风险的可能性减少11.86%。在发生事故时，安全带能有效保护驾驶员的头部并能防止驾驶员被甩出车外。

3.2.4 安全气囊起爆

驾驶座安全气囊起爆会显著增加驾驶员的伤害程度。边际效应结果显示，驾驶座安全气囊起爆后，驾驶员遭受可能受伤、非失能伤害以及失能伤害或死亡的风险分别增加1.74%、7.24%以及3.93%。前人发现，在车内安装侧帘式安全气囊，能有效降低翻车事故严重性[19]，故可建议汽车厂商对新组装的货车统一安装侧帘式安全气囊。

3.2.5 饮酒或吸毒

饮酒或吸毒变量的参数服从N(0.462, 0.3672)的正态分布，表明89.62%的驾驶员在饮酒或吸毒后更容易发生严重的事故，而10.38%的驾驶员在饮酒或吸毒后更不容易发生严重的事故。此差异性结果可归因于部分驾驶员对酒精和毒品的敏感性较差，少量的酒精或毒品基本不影响其对车辆的操控能力。边际效应结果显示，驾驶员在饮酒或吸毒后遭受死伤的风险最大可增加10.10%，这与Q.WU等[6]的研究结论类似。

表3 混合有序Probit模型中自变量的边际效应

3.2.6 被甩出车外

驾驶员被甩出车外变量的参数服从N(1.300, 0.4262)的正态分布，表明99.89%的驾驶员被甩出车外后更容易受严重伤害，而0.11%的驾驶员更不容易受严重伤害。这可能是因为货车发生翻车时，驾驶员被甩出车辆后，着地区域不同，如路面、河流、沟渠等，故而受伤等级也存在一定的差异。边际效应结果显示，被甩出车外后，驾驶员遭受非失能伤害和失能伤害或死亡的概率分别增加18.63%和29.74%。系安全带能有效防止驾驶员被甩出车外，故交通管理部门要加大对不系安全带的处罚力度，并积极宣传不系安全带的危害。

3.2.7 未按规定车道行驶

驾驶员未按规定车道行驶分别增加发生可能受伤(1.52%)、非失能伤害(6.12%)、失能伤害或死亡(3.26%)概率。笔者提出的未按规定车道行驶，主要指跨车道分隔线行驶，这是一种车道偏离驾驶行为。研究表明，欧洲90%的翻车事故以及美国40%的翻车致死人数由车道偏离导致。因此，未按规定车道行驶是一种非常危险的驾驶行为。因此，有必要为车辆安装车道偏离预警系统，一旦车辆发生偏离车道行为，能及时提醒驾驶员。

3.2.8 重型货车

相比于轻型货车和中型货车，重型货车更容易导致驾驶员遭受严重伤害。例如，重型货车驾驶员失能伤害或死亡风险的可能性将增加3.93%。这是因为重型货车具有更高的重心和轴重，从而更容易发生严重的翻车事故。因此，可以考虑为重型货车安装电子稳定辅助装置。

3.2.9 车辆右转

车辆右转变量的参数服从N(-0.766, 0.9272)的正态分布，表明79.67%的驾驶员在车辆右转时更不容易受严重伤害，而20.33%的驾驶员在车辆右转时更容易受严重伤害。这可能是因为车辆在不同交叉口右转时，信号控制、转弯半径以及交通流量存在差异，从而导致这种异质性效应。边际效应结果显示，车辆右转分别降低发生发生可能受伤(7.93%)、非失能伤害(13.99%)、失能伤害或死亡(4.24%)的概率。这在很大程度上是因为车辆右转时一般没有冲突车流，并且在交叉口右转时行驶速度较低，从而更不容发生严重的翻车事故。

3.2.10 不良天气

不良天气情况下驾驶员遭受可能受伤、非失能伤害以及失能伤害或死亡的概率分别降低2.30%、6.08%以及2.49%。这在较大程度上是因为驾驶员在不良天气下会更加谨慎地驾驶，从而更不容易发生严重的翻车事故[20]。

3.2.11 道路限速值

在高限速值高的道路上行驶，货车驾驶员遭受严重伤害的可能性越高。边际效应结果显示，道路限速值每增加1 mph，可能受伤、非失能伤害以及失能伤害或死亡的发生概率分别增加0.05%、0.15%以及0.07%。

3.2.12 车辆出厂年龄

车辆出厂年龄与驾驶员伤害程度显著相关，并且车辆出厂年龄越大，发生严重翻车事故的可能性越大。边际效应结果显示，车辆出厂年龄每增加一年，可能受伤、非失能伤害以及失能伤害或死亡的发生概率分别增加0.10%、0.31%以及0.14%。这说明了随着科技的进步，新型车辆的安全等级更高，交通管理部门需要定期为老车型进行严格的年检。