地磁计转数定时修正引信的定距精度研究

张小禄，李海蓉，丁 毅

(西北机电工程研究所， 陕西 咸阳 712099)

为了提高近程防空反导武器系统的毁伤能力，提高对目标的毁伤概率，弹药精确起爆控制已经成为弹药信息化发展的一个主流方向。由于弹丸初速的跳动，导致弹丸按一定时间进行定时起爆时存在较大的弹目偏差。弹丸的炮口初速是影响弹丸飞行特性和弹目偏差的重要因素[1]。近年来，线圈靶、光电靶、多普勒雷达测速仪、通断靶电涡流测速、激光靶等测速技术在我国己取得了长足的进步，并日臻完善[2]。

地磁计转数定时修正技术通过弹丸在脱离身管约束后，弹丸自主测量在近炮口处弹丸旋转转数，根据旋转圈数与飞行距离的关系，实现弹丸自主测量弹丸速度，并根据该速度实时修正起爆时间，从而实现弹丸高精度定距起爆。地磁计转数法具有无源测量、信号强、易处理的优点，特别适合在小口径弹上应用[3]。基于地磁计转数定时修正技术的弹药可实现高精度定距起爆，且通用性强，可在旋转弹的引信上普遍应用。该技术是实现小口径弹药精确炸点控制的重要途径之一。

本文介绍了基于地磁计转数速度测量技术的原理，介绍了一种基于计转数测速定时修正引信系统，并对基于该原理的引信系统定距精度进行了综合分析，建立了数学计算模型，为工程研发工作提供理论依据。

1 地磁计转数速度测量原理

地磁计转数速度测量技术利用地磁传感器感应地磁场方向的变化，当地磁线与线圈平面法线存在一定角度，线圈以一定角速度绕平面轴线旋转时，在线圈内将产生感应电动势，弹丸每旋转一周，地磁传感器输出一个周期的正弦波信号。地磁传感器基本原理示意图见图1[2]。

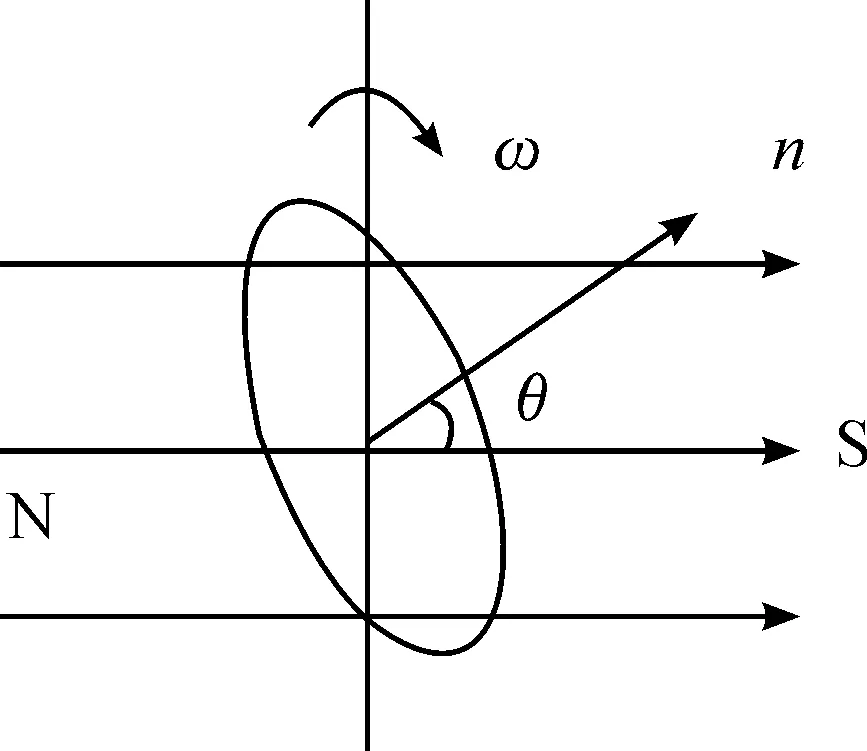
图1 地磁传感器基本原理

计转数速度测量技术采用内置在引信中的地磁传感器测量弹丸转速，通过弹丸导程与转速的关系计算弹丸在炮口处的飞行速度。发射弹丸出炮口后解脱身管膛线约束，高速旋转前进，由于火炮后效应的作用，弹丸轴向速度继续增加，但弹丸转速不再增加，在出炮口的一定距离内，可以将弹丸旋转角速度视为常数。通过测得弹丸出炮口时的角速度值，可以计算出弹丸出炮口飞行速度。由实测的弹丸出炮口转速，结合火炮的身管缠度，计算弹丸在炮口的速度值。其计算公式如下[5]：

(1)

式中：v0为出炮口弹丸速度;ηg为身管膛线缠度;ω0为出炮口弹丸转动角速度;D为弹丸直径;γg为膛线缠角。

从公式可以看出，火炮身管膛线缠度、弹丸直径以及炮口转速是影响弹丸初速的主要因素。其中火炮膛线缠度、弹丸直径是火炮固定参数，弹丸炮口转速则通过地磁传感器转动周期，通过弹载时钟进行测量，可测得弹丸炮口处的弹丸平均转动速度ω0。

2 计转数测速定时修正引信系统

基于地磁及转速速度测量原理，本论文介绍了一种基于地磁计转数测速定时修正引信系统，该系统利用武器系统对目标的探测信息，通过预先装定标准条件下的弹丸飞行时间、引信自主测量弹丸速度、根据实测弹丸速度实时修正引信定时时间、引信高精度定时等技术，实现弹丸高精度定距起爆的功能。系统工作原理图如图2。

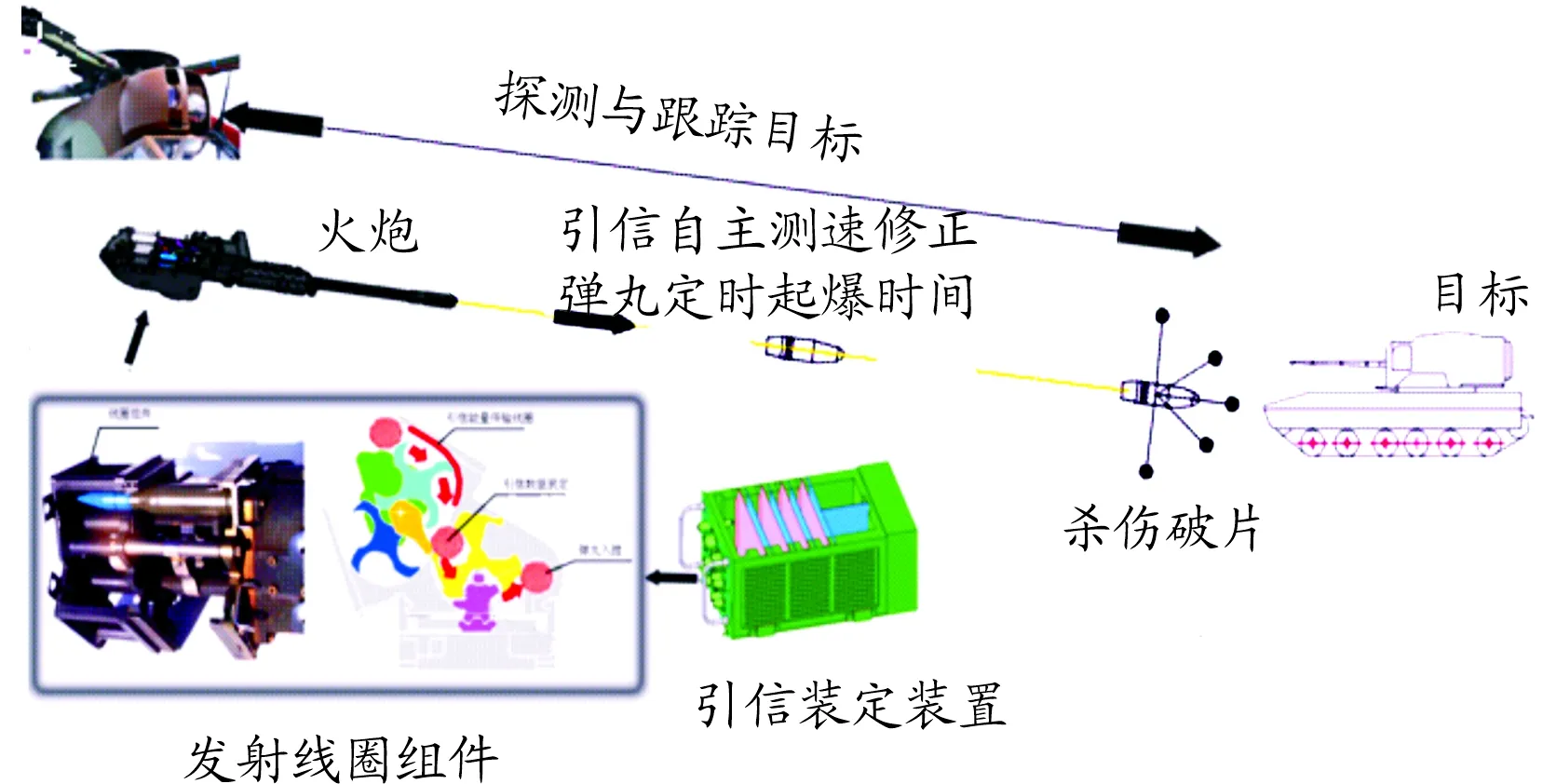
图2 地磁计转数定时修正引信工作原理图

弹丸发射前，引信装定装置实时接收武器系统提供的目标信息，解算弹丸在标准条件下弹丸飞行至目标的时间，并对该时间信号进行编码调制；弹丸在运行至身管膛内前，引信装定装置将时间编码调制信号进行功率放大，采用感应装定的方式，将时间信息传输至引信，并存储于引信内部存储器中；弹丸击发后，引信中的电路系统上电工作，读取标准条件下的弹丸飞行时间，电路系统在弹丸出炮口后一定距离内根据地磁传感器旋转产生的信号计算弹丸飞行速度；引信通过实测弹丸速度实时计算、修正弹丸飞行至目标的飞行时间，引信电路系统同时启动内部定时器，当计数到时，引信作用并引爆弹丸，从而实现弹丸精确定距起爆。

3 引信定距精度分析

根据上述技术方案，假设某弹丸口径为30 mm，对影响该引信定距精度的主要因素进行分析，对系统定距精度进行了理论计算。

3.1 测速误差分析[6]

由速度计算公式：V=S/T，及以式(1)中测速原理，由于火炮导程固定，因此弹丸旋转一圈的距离固定，则速度计算公式中S视为定值。计转数测速方法的速度测量误差主要由速度测量时间内弹丸旋转周期衰减导致的误差及测量误差组成。

1) 旋转周期T衰减误差分析

根据柔格里(E.Roggla)公式，对线膛炮弹丸外弹道旋转角速度衰减规律进行计算，公式见式(2)：

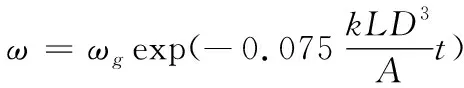
(2)

式中：ω为t时刻弹丸旋转角速度((°)/s)；ωg为弹丸炮口旋转角速度((°)/s)；L为弹丸长(m)；D为弹丸直径(m)；A为弹丸极转动惯量(kg·m·m2)；k为修正系数。

受弹丸稳定要求，一般有L≈(5～6)D，而A∝D5。可得：

进而将柔格里公式改写为：

(3)

式中：α为常系数1.115×10-3m/s。

其中t为测速时间，且根据式(1)测速原理，设定测速时间t≤10Tg(Tg为弹丸出炮口出的旋转周期)，可得：

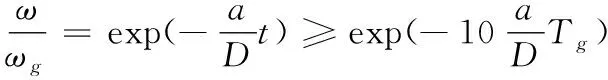
(4)

以某30 mm武器(设定其旋转周期T<1.2 ms)为例，代入上式可得：

则有：(ω-ωg)≤0.000 4ωg

因此：

2) 旋转周期T测量误差分析

计转数测速法采用模数转换方式，实现对弹载地磁传感器输出信号旋转周期的测量，通过累计测量多个旋转周期时间的方式，降低测量误差。此处设定模数转换采样率为10 MSPS、即采样周期为0.1微秒，可以得出：在弹丸飞行10个旋转周期内，信号测量导致的时间误差最大值为0.2 μs，即：

测量速度误差为：

以某30 mm武器(设定弹丸旋转周期T>0.8 ms，弹丸初速为810 n/s)为例，代入上式可得：

根据上述两种误差计算，可看出运用于某30 mm武器测速误差为±0.34 m/s，采用3δ原则，则测速精度为1.26‰。

3.2 引信定时时间解算误差分析

弹载引信定时修正解算模型采用与弹药射表弹道方程相拟合的方式，根据某引信定时时间解算模型的设计经验，可实现较高的解算精度。综合弹载引信电路系统的数据处理能力，中小口径弹药弹载引信定时修正解算模型在 1 000 m 斜距范围内，可控制解算误差≤3 ms。

3.3 引信定时精度分析

引起引信计时误差的主要因素为计时电路中振荡器频率稳定性和分辨率。现代电子技术中，通过优化电路参数，LC振荡器频率稳定性可达到10-4量数量级。

设：计时振荡器频率为10 000 Hz；稳定偏差为1 Hz；频率分辨率为±1 Hz；设弹丸速度为810 m/s、弹丸转速为1 200转/s、1 000 m弹丸飞行时间为tg为1 883 ms。则频率稳定性导致的计时误差为：

振荡器分辨率导致的计时误差为：

则由计时电路引入的相对计时误差为：

3.4 定距误差分析

根据以上分析，当综合考虑弹载引信测速精度、引信定时时间修正解算误差、定时时间误差时，可综合得出引信炸点误差范围。

假设弹丸初速为810 m/s、炸点距离为1 000 m、据试验数据统计弹飞时间为1 883 ms。则当测速误差为1.26‰、解算模型误差时间为3 ms、电子部件计时误差1.05×10-4时，其分别导致的炸点误差为：1.0 m、1.6 m、1.06 m，可视上述3个误差源相互独立，则有定距误差Δs为[7]：

取95%的置信度时，则包含因子k=2，定距误差扩展不确定度为U=2×Δs=4.32 m。

4 验证

通过对计转数测速定时修正计时原理分析及对定距误差的计算，证明了基于该技术可实现弹丸高精度炸点精确控制。 在此基础上对基于该原理的某系统进行了1 000 m立靶试验，试验结果表明，在理想的试验平台下，射弹10发，统计炸点位置与预定位置偏差的绝对值，计算得组平均定距误差为4.8 m，与理论分析较为吻合。根据理论计算分析，在工程实践中，可以通过提高采样率、降低解算误差、提高计时时钟频率稳定性等措施，进一步降低定距误差。

5 结论

采用基于地磁计转数测速定时修正技术，根据每发弹丸实时测量的炮口初速、并根据初速实时修正弹丸飞行时间、引信高精度定时，可以实现较高的引信定距精度，从而有效提高弹药对目标的精确打击能力。本论文从影响定距精度的各因素进行综合分析，对炸点精度进行研究和分析，为基于地磁计转测速数定时修正技术引信的研制提供较大的借鉴意义。