基于深度卷积神经网络的多飞行器构型保持研究

槐泽鹏，王洪波，龚 旻

(中国运载火箭技术研究院， 北京 100076)

2016年“人工智能”被写入我国“十三五”规划，2017年国务院发布《新一代人工智能发展规划》，在顶层文件驱动下，社会各行各业都在加大对人工智能的研究与投入。深度学习作为通向人工智能的途径之一[8]，已经在图像识别[2，9-10]、语音识别[11-12]、文本识别[13-14]、多模态交互[15]等领域取得诸多成果。尤其是谷歌举办的ImageNet比赛：从2012年的AlexNet[3]，到2013年的ZF Net[4]，2014年的VGGNet[5]、GeogleNet[6]，再到2015年的ResNet[7]，这些对深度学习的发展具有里程碑式意义。同时，如Facebook、Microsoft、Amazon等企业开发了第三方深度学习框架以支撑相关学者的研究，如TensorFlow、MXNet，Caffe、Keras等，这些为深度学习在其他行业的普及和应用奠定了良好基础。

在国防军工领域，协同作战是近些年来兴起的被认为具备非对称领先优势的新作战模式，世界各军事大国都在开展相关研究和项目，如空中协同作战SoSITE[20]、拒止环境协同作战CODE[21]、无人机协同作战“山鹑”Perdix[22]等。多飞行器协同是协同作战发展的必然趋势，当前此方向的研究主要集中于关键技术攻关，如任务规划技术[17]、飞行器数据链技术[18]、协同路径规划技术[19]等，其中构型保持对实现多种飞行器编队模式具有基础支撑意义[16]。因此，本文旨在将深度学习技术应用于多飞行器构型保持问题，以获得性能更加良好的构型保持算法。

1 问题描述及飞行器模型

本文旨在解决以下问题：3枚飞行器在中段飞行时在当地铅锤面内持续保持正三角形构型，如图1所示。保持的构型如图2所示。

图1 本文欲解决的构型保持问题示意图

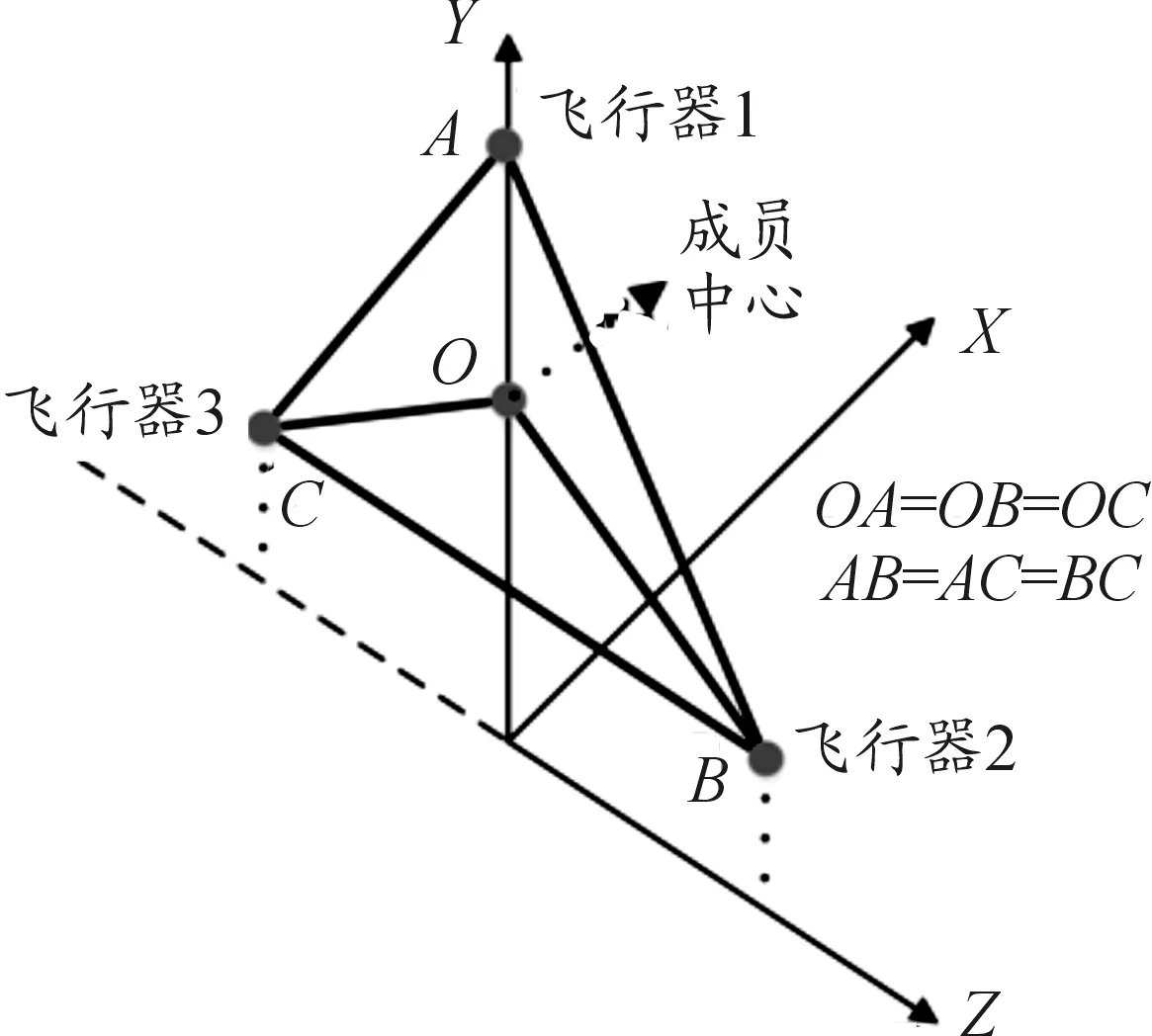
图2 构型保持示意图

评判构型保持的效果用如下方式表示：在图3中，蓝色点是飞行器当前位置，成员中心为黑色点，在铅锤面内以黑色点为中心构造正三角形，认为此三角形的3个顶点为3个飞行器的期望位置。则各飞行器实际位置与期望位置的距离认为是构型保持的误差。

图3 构型保持误差示意图

飞行器的动力学模型如式(1)所示：

sinψ=cosαcosβsinσ-sinαcosσsinν+

cosαsinβcosσcosν

sinφcosψ=cosαcosβsinθcosσ+

sinα(cosθcosν+sinθsinσsinν)-

cosαsinβ(-cosθsinν+sinθsinσcosν)

sinγcosψ=sinαcosβsinσ+cosαcosσsinν+

sinαsinβcosσcosν

(1)

式(1)为飞行器基本的动力学方程，由于与本文研究内容不直接相关，所以不详细介绍(可详见文献[1])。这里需要指出的是，上述动力学模型的控制指令是攻角αc和倾侧角γc，控制飞行器飞行的方式是每隔固定时间间隔(如 0.5 s)给出一次指令，即通过设计这两个量在每次数值积分时的值(数值积分的步长等于指令时间间隔)，来解决本文旨在解决的问题。

此控制指令已经通过传统优化方法(后面简称“优化法(FKCG)”)得到并且实现了构型保持，其效果见图4，但是存在一个重要缺陷：优化法的速度慢，计算量大，在python环境下优化一次需约2.3 s，难以满足飞行器飞行高速高动态对指令快速在线生成的要求。因此针对这一缺陷，本文旨在设计一个深度神经网络模型以快速生成控制指令。

图4 成功构型保持效果的实例曲线

2 基于深度卷积神经网络的构型保持模型

2.1 深度神经网络模型

1) 输入。对每枚飞行器选取17个状态变量作为输入，共51个变量。同时借鉴机器视觉中图像用像素矩阵元素表示的做法，将其组合为8*8矩阵，剩余8×8-51=13个空格均置零，如图5所示。

图5 输入矩阵元素

2) 输出。输出为3个飞行器的控制指令，即3个攻角3个倾侧角。

3) 神经网络模型。设计神经网络模型时有以下5项考虑：

① 由于飞行器动力学模型为强非线性的复杂模型，因此选取神经网络的深度即层数时，不能因模型容量小而导致欠拟合；

② 加深网络深度后，为避免层数加深反而学习效果未提升甚至衰减的现象，引入“残差结构”和“归一化层”；

③ 采取卷积神经网络和全连接层进行特征提取；

④ 由于输入矩阵不同于图像矩阵中像素有连续性，因此不考虑降低敏感性及保留主要特征，这里卷积层后不连接池化层；

⑤ 输出层采取并联结构，分别输出攻角和倾侧角。

最终，经过对比试验和综合选择，搭建了19层神经网络，如图6所示。其中，conv代表卷积层，均使用3*3卷积核，步幅为1，填充为1；BatchNorm代表批量归一化层；Activation 代表激活层，均采用Tanh函数；Dense代表全连接层；每个方块最后面的数字代表输出的通道数。

图6 神经网络模型结构示意图

2.2 模型训练

1) 训练方法。模型训练的损失函数采取误差平方，正则化采用权重衰减惩罚项，衰减系数为0.000 1，损失函数如式(2)所示。

(2)

其中，αi和νi为神经网络输出；αic和νic为样本输出。这里定义训练误差为(L/6)0.5*57.3，其物理意义是角度制下6个角度的平均误差。

模型训练的优化方法采取小批量随机梯度下降法，由于输出为弧度制角度，数值较小，因此学习率应设置较小以敏感微小变化，初始值为0.1。为避免学习率过大导致训练结果持续震荡但不衰减，考虑当训练误差在近20个周期内的标准差小于某一设定值(0.002°)时，缩小学习率以使训练误差能够减小；如果近50个周期内训练误差的标准差小于某一设定值(0.002°)，认为此时模型训练误差无法再继续减小，即已到模型拟合准确程度的上限，停止训练。上述学习率缩减及训练终止条件如图7所示。训练硬件采用阿里ecs.g5.large型云服务器。

图7 训练终止条件框图

2) 训练结果。以成功构型保持的实例即图4作为训练样本，训练结果如图8、图9所示。

图8 训练误差曲线

图9 学习率曲线

在图8中，训练误差持续减小，最终稳定于0.025°附近，其物理意义是攻角或倾侧角在神经网络的输出值与样本值仅相差约0.025°，对于这两个角度物理量，这个量级十分小，这一结果验证了深度神经网络模型和训练方法的有效性。在图9中，可以看到学习率经历了3次缩减，第一次缩减带来训练误差明显下降，但后两次没有，这就说明此时已经不是由于学习率过大导致训练误差无法减小，而是已经到达模型拟合的能力上限，同时结合图8也验证了学习率缩减策略的有效性。

3 泛化误差累积与校正

3.1 泛化误差累积

神经网络的泛化误差是不可避免的，并且永远大于训练误差。当这个误差足够小时，例如在图像分类中我们可以认为大部分情况下图像分类正确，只有一小部分分类错误。但是在飞行器运动问题中，控制指令攻角αc和倾侧角γc是每隔固定时间间隔就给出一次，一段飞行轨迹一般存在上万个这样的间隔，所以当上万次指令都存在泛化误差时，尽管每次误差的量级可能很小(10-2度)，但泛化误差累积仍会对飞行器运动带来明显影响。

图10是只使用神经网络解算控制指令得到的飞行器轨迹，可以看到此时弹道已发生整体偏移，并且此时3个飞行器的构型保持误差持续上升。

图10 泛化误差累积对飞行器轨迹的影响曲线

3.2 校正

针对泛化误差累积对飞行器运动带来显著影响这一问题，考虑采取以下设计来校正累积的泛化误差：

1) 对神经网络解算的控制指令加上一个校正量，以解决泛化误差累积的问题；

2) 校正量的值是优化法解算的控制指令与神经网络输出控制指令的差值；

3) 校正量每隔n个制导周期重新计算1次；

4) 认为校正周期计算得的校正量能够近似代表校正后n个周期内神经网络与优化法解算的差值。

最终，“智能-校正”算法如图11所示，第4节将叙述其构型保持效果。

图11 “智能-校正”算法示意图

4 仿真分析

本节针对不同的n进行仿真，当n=0时，即每个周期都校正，即为纯优化解算控制指令，其仿真结果如图4所示；当n=∞，相当于不校正，即为纯神经网络解算控制指令，其仿真结果如图10所示。这里一个周期为0.01 s，则当n=100时即每间隔1 s进行一次校正。可以直观判断，n越小，校正越频繁，泛化误差累积的影响越小，构型保持效果越好。

这里给出n取不同值时的构型保持误差如表1所示，和n=50、100、130的飞行器轨迹分别如图12～图14所示。

表1 不同n下构型保持误差

图12 n=50时的仿真曲线

图13 n=100时的仿真曲线

图14 n=130时的仿真曲线

从以上仿真结果可以看出：

1) “智能-校正”算法解决了泛化误差累积的问题，仿真结果验证了其有效性；

2) 当n≤140时，“智能-校正”算法的构型保持误差之和基本不变，维持在一个较小数量(均小于10 m)；

3) 当n>140后，随着校正间隔越来越长，泛化误差累积的影响越来愈大，构型保持误差持续上升，直到n=∞(不校正，纯神经网络)，构型保持误差之和为620.58m；

4) 考虑计算速度，仿真时我们采取相同的计算条件(Python语言、PyCharm平台、MXNet框架)，神经网络输出一次控制指令的时间约为0.38 s，而原优化方法解算一次控制指令的时间约为2.3 s，速度提升了约6倍。这一结果实现了本文设计神经网络的初衷：快速生成控制指令；

可以说，基于深度神经网络的智能-校正算法兼顾了精度和速度。精度方面，通过校正消除了泛化误差累积的影响，实现了较小构型保持误差；速度方面，原优化方法解算一次指令需约2.3 s，而神经网络解算一次指令只需约0.23 s，速度提升了约6倍。同时给出了不同校正间隔时间与构型保持误差的关系，当对构型保持误差要求不高时，可适当增大校正间隔时间以带来更少的计算量；反之需高精度构型保持时，可减小校正间隔时间。

5 结论

基于卷积层、全连接层、归一化层和残差网络设计了一个19层深度神经网络，并采用权重衰减正则项和可变学习率，成功将神经网络训练误差降低至约0.025°。神经网络应用于飞行器制导过程时，存在泛化误差累积的现象，对此设计校正环节以避免带来构型保持误差。通过飞行仿真验证了“智能-校正”算法的快速性和有效性，给出了不同校正间隔时间与构型保持误差的关系。