军用多轮分布式电动车辆驱动力协调控制

刘春光，马晓军，王科淯

(中国人民解放军陆军装甲兵学院 兵器与控制系， 北京 100072)

军用多轮电驱动车辆作为新型作战平台，由于具有驱动轮相互独立、供电方式多样等特点，可适应多种作战需求，可通过搭载装配不同装备组合胜任包括运输、突击、救援等各类作战任务，是近年来各国国防科研领域的关注热点之一[1]。作为战场人员装备输送平台，需要具备较高的越野能力，在复杂路面仍能保持较好的稳定性、机动性，但同类车辆多存在车身长，质量大等特点，这使得车辆的稳定性、机动性的协调控制成为研究的难点问题[2-3]。

以往相关研究多以提高车辆稳定性或平顺性作为控制目的[4]，上层运动跟踪控制器考虑车辆运动状态及路面情况，计算出横摆角速度和质心侧偏角给定值，然后由下层转矩分配控制器分配至各驱动轮[5-6]。关于多轮车辆的控制研究中，只有少数学者考虑通过协调控制，实现车辆的双重转向，即在车轮纯滚动转向的基础上加入滑移转向，通过减小转向半径，提高车辆机动性。但控制车辆实现双重转向的研究中，多数仅考虑了车辆状态，未结合驾驶意图分析[7-9]。

本研究设计了一种协调控制策略，上层控制器包括驾驶意图解释模块、横摆控制模块，在计算横摆角速度给定值时，通过控制车辆双模转向中滑移转向与纯滚动转向比例，综合考虑车辆转向半径与横摆角速度控制问题，使上层控制兼顾稳定性与机动性控制；下层转矩分配模块中，采用模糊控制，依据车辆状态和行驶控制目标，协调分配各驱动轮转矩给定[10]。

最后在ADAMS与Simulink联合仿真环境下进行典型工况仿真试验，验证控制方法的有效性，为同类型装甲车辆行驶控制设计提供参考[11-13]。

1 控制器设计

分布式驱动协调控制器包括3个模块：驾驶意图解释模块、横摆控制模块和转矩分配模块。控制器逻辑框图如图1。

图1 分布式驱动协调控制器逻辑框图

该驱动转矩目标值经Flexray总线下发轮毂电机控制器，电机控制器采用防滑控制算法对各驱动轮进行驱动控制，实现车辆多轮独立电驱动行驶。

1.1 驾驶意图解释模块算法

基于8轮双前桥转向车辆双轨二自由度模型，建立车辆参考模型

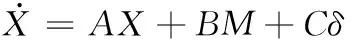
(1)

式中：X=[βγ]T为车辆的状态变量；δ为转向轮转角；M为横摆力矩；A、B、C为车辆状态参数矩阵，具体表达式如式(2)中所示。

可推导，质心侧偏角和横摆角速度在双前桥转角δ输入下状态空间表达式：

(2)

其中：Li为各桥车轮距重心的纵向距离；Cαi为各车轮侧片刚度系数；Iz为车辆垂向转动惯量。

可推导出，自然转向下横摆角速度为

(3)

常规地，以横摆角速度γ为控制目标变量，通过调节车辆横摆力矩M进行运动轨迹跟踪控制，可实现轮式车辆的理想自然转向。为满足装甲车辆的战术使用要求，引入履带式车辆滑移转向机理，实现自然转向和滑移转向的叠加作用，可使车辆具有更小的转向半径，其基本思路是引入双模转向系数σ，以(1+σ)γ为控制量进行运动轨迹跟踪控制。

问题转化为：在一定的转向轮转角δ、车速Vx、路面附着系数μ条件下，在稳定运行区域内对双模转向系数σ(σ≥0)进行寻优，使车辆转向半径R(σ)与车辆质心侧偏角β(σ)的加权之和最小[12]。

为此，设计寻优目标函数：

(4)

式中：Kt1、Kt2分别为车辆转向半径、质心侧偏角变量的权值；R*、β*分别为车轮纯滚动条件下(σ=0)车辆自然转向的半径、质心侧偏角。

约束条件包括侧向力小于路面最大附着能力和质心侧偏角-质心侧偏角速度相平面轨迹在稳定区域边界内，整理如式(5)和式(6)所示：

m(1+σ)γVx≤μmg

(5)

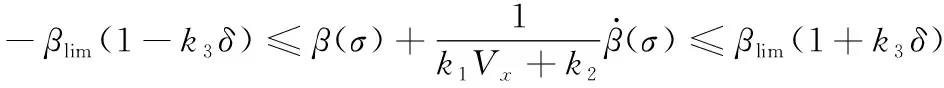
(6)

在实际应用中，采用ADAMS软件构建车辆多体动力学模型，以转向轮转角δ、车速Vx、路面附着系数μ等边界条件，仿真在不同的双模转向系数下车辆稳定运行的车辆转向半径R(σ)与车辆质心侧偏角β(σ)，由仿真数据拟合出σ～R(σ)、σ～β(σ)曲线。取权值K1=0.6，K2=0.4，在约束条件范围内采用二分法寻优，可获得双模转向系数σ的最优解，进而确定轨迹跟踪控制的目标变量(1+σ)γ。

1.2 横摆控制模块算法

以驾驶意图解释模块确定的(1+σ)γ为控制变量(为简化公式，下文以γd表示(1+σ)γ)，采用滑模变结构算法计算期望横摆力矩：

选取滑模面

S=Δγ=γd-γβ_lim

(7)

采用指数趋近率

(8)

式中：h1>0，ε>0，可得：

(9)

将式(9)与车辆横摆运动方程联立，可得车辆横摆力矩：

(10)

以左转为例，为实现式(10)横摆力矩，单侧驱动轮的总转矩分别为：

(11)

式中：TL、TR分别表示左、右侧4个驱动轮转矩之和；Td为根据加速踏板信号解析的需求总转矩。

至此，问题转化为如何将单侧驱动力矩TL、TR分配到4个电驱动轮上。

1.3 转矩分配模块算法

以车辆姿态传感器采集的俯仰角度θ、车辆纵向加速度ax为输入变量，采用模糊控制算法，输出同侧4台轮毂电机的扭矩分配系数，从第一轴至第四轴分别表示为ξ1、ξ2、ξ3、ξ4。模糊控制输入量和输出量的语言变量设定为{小，中，大，很大}，模糊子集设定为{S，M，L，V}。由于三角隶属度函数具有灵敏度高的特点，采用三角函数作为θ、ax和ξ1、ξ2、ξ3、ξ4的模糊子集隶属度函数，分别如图2所示。

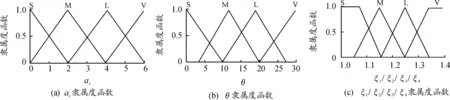
图2 输入量和输出量隶属度函数

制定表1所示的模糊控制规则。

表1 模糊控制规则

将转矩分配系数ξ1、ξ2、ξ3、ξ4进行归一化处理：

(12)

(13)

(14)

(15)

式中：τ1、τ2、τ3、τ4分别为归一化后的第一轴至第四轴转矩分配系数。

1.4 防滑驱动控制

由于篇幅限制，且驱动防滑控制部分非本文主要创新部分，所以只做简要介绍。具体方法可参考文献[12]。

由于各个驱动轮的载荷不同以及行驶路面条件的差异，附着条件较差的驱动轮不一定能输出期望的转矩，从而达不到整车牵引力以及期望横摆力矩的需求，影响车辆转向的稳定性。基于此，在单个车轮得到驱动转矩给定值之后针对单个车轮进行防滑控制，将车轮滑转率控制在最优值附近，最大限度利用路面附着力，同时，将因防滑控制而减小的驱动力增加到同侧其他未滑转车轮上，最大限度满足整车驱动力和横摆力矩需求。

1.5 轮胎模型

考虑到上层跟踪控制系统的工作涉及到车辆的非线性运行区，简单的线性轮胎模型必然无法满足实验精度要求，以往有学者在类似的研究过程中利用魔术公式建立轮胎模型，但魔术公式涉及到的拟合参数较多，计算较复杂，易与实时性要求冲突。

本文根据控制精度需要，选择Dugoff轮胎模型，该模型旨在描述轮胎非线性侧向力，涉及参数比魔术公式少，其描述如下：

(1)

式中，Cαi表示轮胎的侧偏刚度，与垂向载荷Fzi相关。

当轮胎的侧偏角发生变化时，会产生一个有时滞的轮胎侧向作用力，这种瞬时的轮胎特性可用一个松弛长度σi描述。进而得到动态轮胎侧向力模型：

(2)

2 ADAMS与Simulink联合仿真验证

为验证本文设计稳定性控制策略的有效性，在ADAMS中建立车辆多体动力学模型，其中包括轮胎模型和满足一般试验工况的地面模型，在MATLAB中建立了包含电机控制器的控制模型。为重点验证车辆控制系统在恶劣路面环境中对车辆的控制效果，进行了低附着路面中速双移线行驶仿真试验。路面附着系数为0.3，目标车速45 km/s。

ADAMS中多体动力学模型的车身及Simulink中电机驱动系统部分参数如表2所示。

表2 车辆及电机驱动系统部分参数

进行仿真试验，得到的行驶轨迹和其他有关曲线如图3～图6所示。

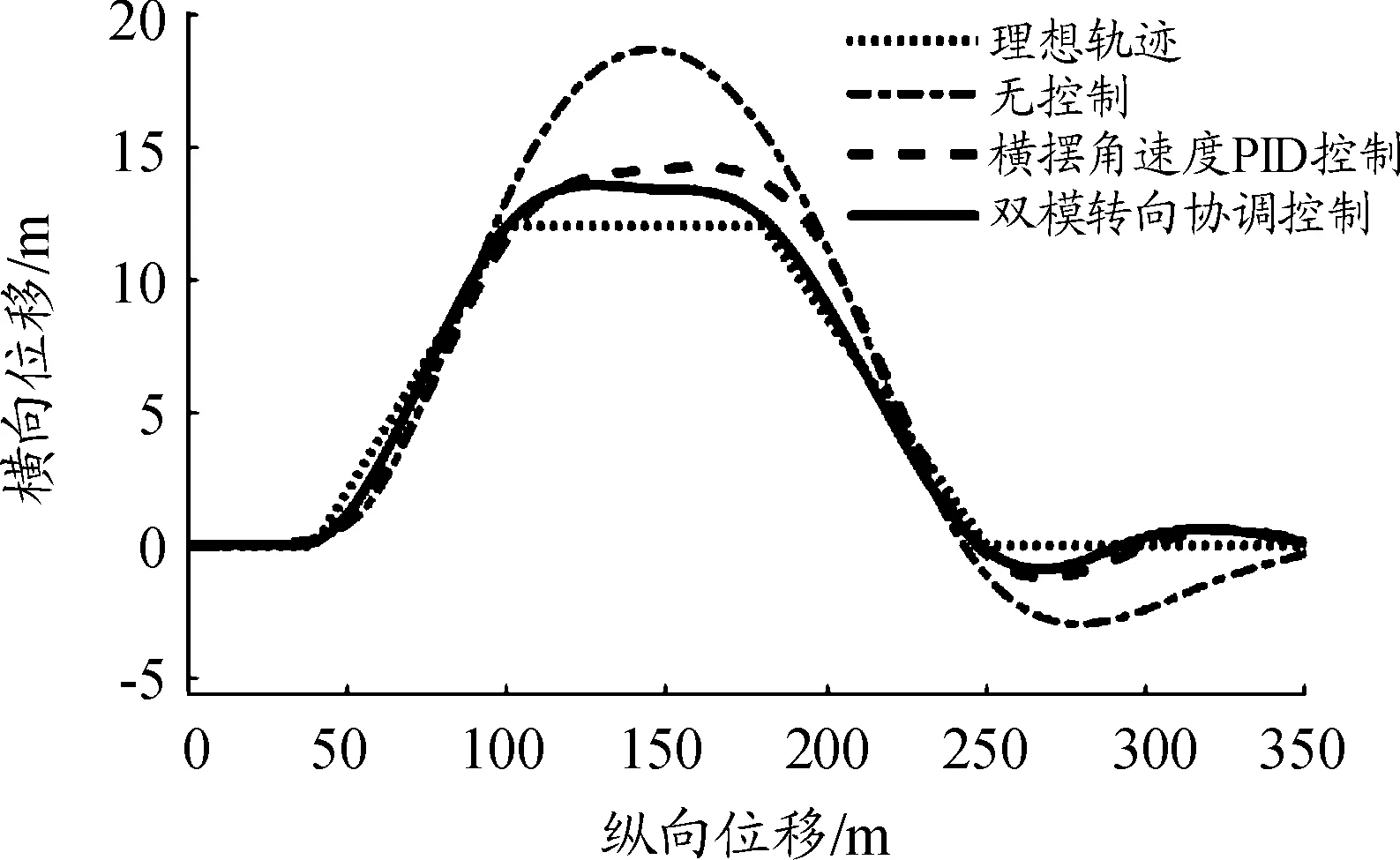
图3 行驶轨迹

图4 目标函数Γ(σ)曲线

比较图1中不同控制条件下的车辆行驶轨迹，可以看出，未施加行驶控制的车辆，无法按照预定轨迹行驶，在实验结尾处仍处于极不稳定的行驶状态，按照传统方法施加控制的车辆行驶过程中的稳定性有明显改观，而采用本文所述控制方法的车辆则具有更好的循迹能力，在每次转弯结束后，都能很快地恢复直线行驶。

图2中为目标函数minΓ(σ)的实时值，可以看出，虽然无论施加控制与否，在开始转弯时，函数值都会出现上升，但由于前两种控制方法未对该函数进行寻优求解，只控制了横摆角速度，未考虑转向半径的优化问题，其中PID控制方法，虽然控制了横摆角速度，但没有考虑转向半径的优化，所以函数值与未施加控制的结果较相似。结合图3易于理解，该控制方法，关注了稳定性控制，但没有直接控制车辆转向半径，所以对机动灵活性的控制较欠缺。综合比较可看出，本文所述方法的函数值上升幅度最小，趋势最平缓。

从图5可以看出，后两种控制方法，对横摆角速度的控制效果相似，而且后一种方法控制效果略优于前者。

图6为文中所述方法控制下各车轮转矩给定值，两侧的车轮、每侧的各个车轮都能依据车辆实际行驶状态、路面状态分配得到不同的转矩给定值。

3 结论

设计一种协调控制策略，驾驶意图解释模块和横摆控制模块构成上层控制器，在进行横摆力矩控制时，不仅控制了代表车辆稳定性的横摆角速度，同时也优化控制了车辆转向半径，从而提高车辆机动灵活性；下层转矩分配模块，采用模糊控制，综合车辆状态及路面情况，分配各驱动轮转矩给定，保证整车力横摆转矩实现。仿真结果表明，上述控制器，能够很好地控制车辆依据驾驶员意图行驶，充分利用多轮车辆具有双模转向的特点，同时控制转向半径与横摆角速度，综合改善车辆行驶时的稳定性与机动性，从各方面促进此类装甲车辆更好地发挥其武器效能。