不同海面风速对量子卫星星舰通信性能的影响*

聂敏 张帆† 杨光2) 张美玲 孙爱晶 裴昌幸

1) (西安邮电大学, 通信与信息工程学院, 西安 710121)

2) (西北工业大学, 电子信息工程学院, 西安 710072)

3) (西安电子科技大学, 综合业务网国家重点实验室, 西安 710071)

量子卫星星舰通信是量子保密通信的重要应用场景之一, 在海面上, 由于不同风速所引起的气溶胶粒子浓度发生剧烈变化, 而气溶胶粒子浓度的剧变, 必然导致星舰量子链路性能的剧烈衰减.然而, 有关不同海面风速与量子卫星星舰通信信道参数关系的研究, 迄今尚未展开.本文根据海面风速与气溶胶的Gras 模型, 分别建立了风速与星舰量子信道误码率、信道容量和信道平均保真度的定量关系.仿真结果表明, 当风速分别为4 m/s 和20 m/s 时, 海洋大气信道误码率、信道容量、信道平均保真度分别依次为4.62 × 10–3 和4.91 × 10–3、0.957 和0.65、0.999 和0.974.由此可见, 风速对海上量子通信性能有显著的影响.因此, 为了提高通信的可靠性, 应根据风速大小, 自适应调整系统的各项参数.

1 引 言

在远离大陆的海洋大气边界层中, 海洋型气溶胶一般包含两类: 海盐气溶胶和二次海洋气溶胶.海盐气溶胶又称为海盐飞沫, 在大气中滞留时间短, 由海风在海面引起的海浪飞溅而产生[1].文献[2]定量分析了恒定方向风对波罗的海的气溶胶粒子数浓度的影响, 为海洋大气循环的研究提供了科学依据.文献[3]分析了热带和亚热带太平洋海域中, 不同天气条件下的气溶胶粒子谱分布特征和新粒子的形成规律.

量子卫星星舰通信是量子保密通信的重要应用场景之一, 量子卫星星舰通信是构建全球性量子通信网络重要的组成部分.2016 年, 由中国科学家自主研制的“墨子号”科学实验卫星在中国酒泉卫星发射中心成功发射, 这为未来覆盖全球的天地一体化量子通信网络建立了基础.2020 年, 中国科学技术大学潘建伟院士团队[4], 在中国德令哈观测站和南山观测站, 实现了基于纠缠的千千米级安全量子加密, 证明了远距离量子加密通信的可行性, 推动了量子卫星网络的实用化进程.同年, 新加坡国立大学量子技术中心联合代尔夫特理工大学[5], 提出了一种量子卫星星座模型, 能够以低延迟在任意两个地面站之间实现量子密钥分发, 为未来卫星量子网络的大规模应用奠定了基础.近年来, 地面量子通信网络的研究也愈加完善.文献[6]研究了基于隐形传态的量子保密通信方案.文献[7]提出了基于纠缠的高效多用户量子加密网络.

量子卫星信号在进入接收端之前, 必然会受到多种因素影响.文献[8]研究了PM2.5 对自由空间量子通信性能的影响.文献[9]分析了K 分布强湍流下自由空间测量设备观的量子密钥分发模型.文献[10]研究了非均匀水流中涌浪运动对水下量子通信性能的影响.文献[11]提出了一种基于软件定义量子通信的量子通信信道参数自适应调整策略,使用该通信策略能够有效提高量子通信系统的生存性及综合免疫力.

本文针对退极化信道, 根据海面风速与气溶胶的 G ras 模型, 分析了不同海面风速对信道误码率、信道容量和保真度的影响, 建立它们之间的定量关系, 进行了仿真实验验证, 为海洋大气背景下自由空间量子通信提供了参照依据.

2 海风对海洋大气气溶胶粒子数谱分布的影响

图1 是量子卫星星舰通信模型, 在图1 中,S 是量子卫星, S1, S2, S3是船舰.其中, 量子卫星是信号发送端, 接收端位于船舰上.由于量子光信号的波长与气溶胶粒子尺寸相近, 当光信号在海洋大气中传输时, 会发生吸收、衰减等现象.实际应用中, 海洋型气溶胶粒子数谱分布可以由对数正态分布来拟合[12]

式中, No为粒子数浓度, rg为粒子的几何标准半径, σg为粒子的几何标准偏差, r 为粒子半径.海洋气溶胶粒子谱分布按照粒子半径分为3 个模态,半径小于0.8 µm 的细粒模、半径在1 µm 左右的中间膜和半径在2—3 µm 的粗粒模[13].根据文献[14,15], 中国南海的海洋气溶胶粒子谱分布由一个细粒模和一个中间膜叠加构成, 中国南海的海洋气溶胶粒子谱分布拟合如图2 所示.图2 中, x 轴为粒子半径, y 轴为粒子谱分布.其中, 细粒模、中间膜的拟合参数取值如表1 所示.

图1 量子卫星星舰通信Fig.1.Quantum satellite-to-ship communication.

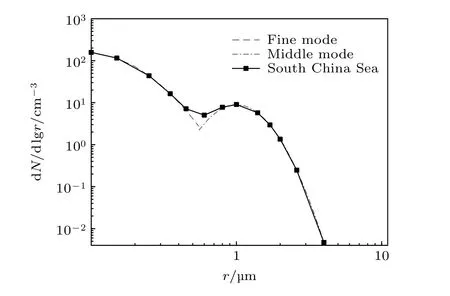
图2 南海气溶胶粒子谱分布Fig.2.Size distribution of aerosol particle in the South China Sea.

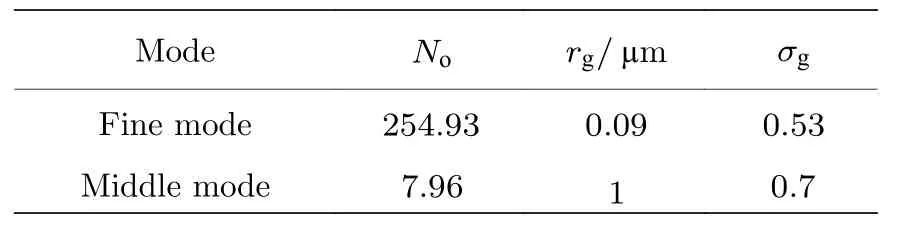
表1 南海气溶胶粒子谱分布各参量取值情况Table 1.The value of each parameter of size distribution of aerosol particle in the South China Sea.

海风引起的海浪飞溅会增加海洋大气边界层内的海盐气溶胶数目, 从而改变海洋大气气溶胶的粒子谱.气溶胶粒子浓度和风速的 G ras 模型可以表示为[16]

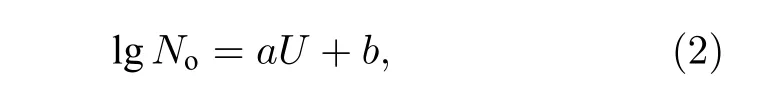
式中, U 为风速, a, b 为与粒子尺度相关的常数.不同海面风速和海洋气溶胶粒子数密度谱分布的关系如图3 所示.图3 中, x 轴为粒子半径, y 轴为粒子谱分布.由图3 可知, 风速会改变海洋大气气溶胶谱分布.当粒径小于0.3 µm 时, 风速对粒子数谱分布几乎不影响.当粒径大于0.3 µm、小于4 µm时, 粒子浓度随着风速增大明显上升.由此可见,海面风速变化会改变气溶胶粒子浓度, 从而影响气溶胶粒子谱分布.

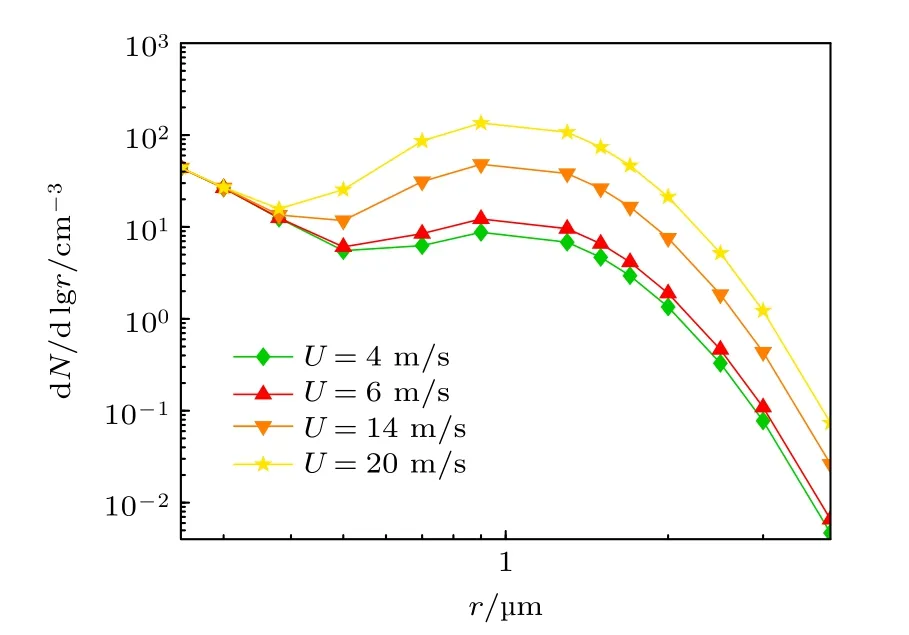
图3 不同风速下的海洋气溶胶粒子谱分布Fig.3.Size distribution of marine aerosol particle under different wind speeds.

3 风速对信道误码率的影响

光量子信号在海洋大气中传输时, 受到气溶胶的影响发生衰减, 最终产生误码.量子信道误码率为接收到的误码比特率和总比特率之比, 可表示为

式中, Qe为海洋大气中气溶胶引起的误码率, Rm为气溶胶引起误码的比特率, Rs为总比特率, Rs可以表示为[17]

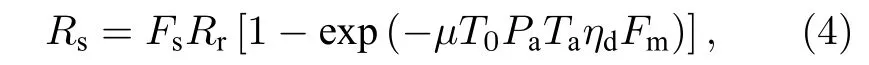
式中, Fs为筛选因子, Rr为发射机脉冲重复率, µ是激光脉冲平均光子数, Pa为单光子捕获概率, Ta为系统装置传输率, ηd为单光子探测器量子效率,Fm为测量因子, T0为海洋大气信道传输率, 其值为

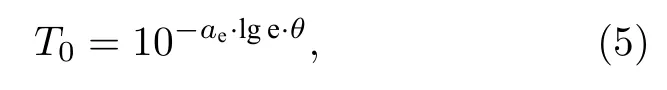
式中, ae为气溶胶的消光系数, θ 为高斯光束发射天顶角.根据Mie 散射理论, 气溶胶消光系数 ae与消光效率因子、气溶胶粒子谱分布之间的关系可以表示为[18]

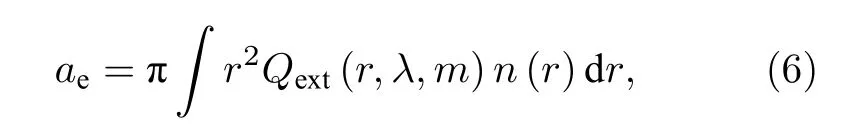
式中, r 为气溶胶粒子半径, n (r) 为气溶胶粒子谱分布.Qext为气溶胶粒子消光效率因子, 可以表示为

式中, λ 为入射光波长, m 为折射率, an, bn, bn为Mie 系数.x 为尺度参数, 可以表示为

Rm可以表示为[8]

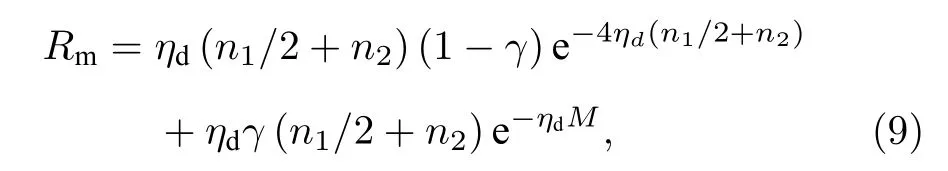
式中, n1为背景噪声引起的光子计数, n2为暗计数, γ 为气溶胶退极化效率因子, γ =1 −10−ae·lge,M =e−aeL+4(n1/2+n2), L 为传输距离.由(4)式、(9)式可得:

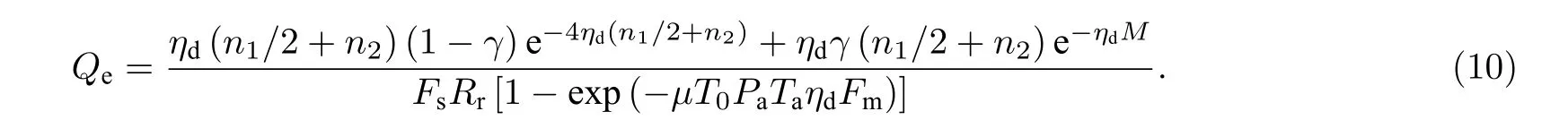
采用波长 λ 等于0.86 µ m , 基膜高斯光束作为光源脉冲, 对于 B B84 协议, Fm=1 , Fs=1/2 , 对于 B 92 协议, Fm=1/4 , Fs=1.本次数值仿真采用 B B84 协议, 在此工作波长下, 单光子探测器的量子效率可达0.65, 这里忽略系统装置传输率, 即Ta=1, 数值仿真各参量取值如表2 所示.

信道误码率与海面风速、传输距离的关系如图4 所示.图4 中, x 轴为海面风速, y 轴为传输距离, z 轴为信道误码率.由图4 可知, 传输距离一定时, 随着海面风速增大, 信道误码率呈上升趋势.传输距离小于 5 0 km , 海面风速不变, 随着距离增大, 误码率显著上升.当传输距离为 1 00 km , 风速 由 4 m/s 变 为 2 0 m/s 时, 误 码 率 由4.62×10−3增大到 4.91×10−3.因此, 海面风速及传输距离对量子通信信道误码率有一定影响, 可根据风速大小调整光量子信号的发射功率, 改善量子通信的通信效果.

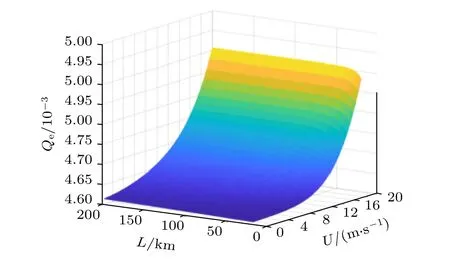
图4 信道误码率与风速、传输距离的关系Fig.4.Relationship between channel bit error rate and wind speed、transmission distance.

表2 信道误码率各参量取值情况Table 2.The value of each parameter of channel bit error rate.

4 风速对信道容量的影响

一个量子态在海洋上方传输时, 会与大气环境发生相互作用, 导致消相干[19].对于退极化信道,量子态的密度算子 ρ 可以通过自旋极化矢量 Ω 表示为

设初始量子态为 α |0〉+β|1〉 , 与海洋大气环境联合演化可以表示为

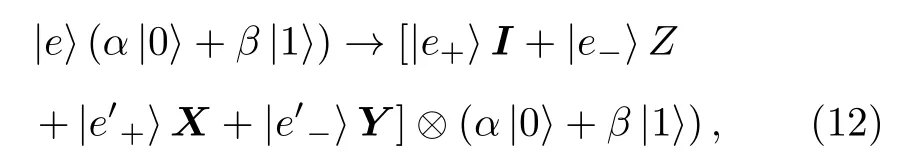
令 | e+〉=|eI〉 , | e′+〉=|eX〉 , | e′−〉=|eY〉 , |e−〉=eZ〉, 则量子态与海洋大气环境组成的复合系统幺正演化可以表示为

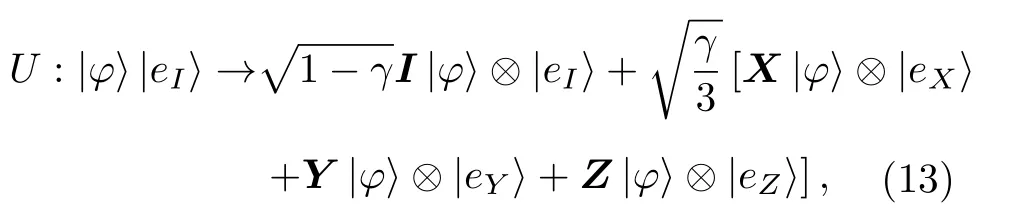
对正交基 { |eI〉,|eX〉,|eY〉,|eZ〉} 求偏迹, 此时量子态的密度算子可以表示为[20]

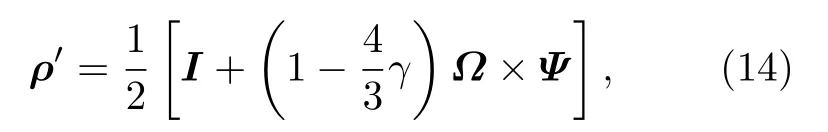
由此可见, 量子态会以概率 γ 退极化, 自旋矢量的大小减小为原来的海洋大气信道可以表示为

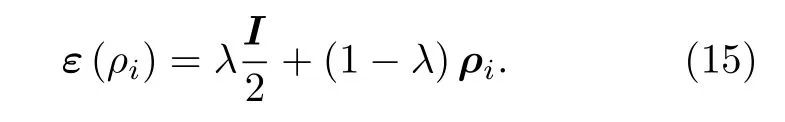
信道容量C 可以表示为[21]

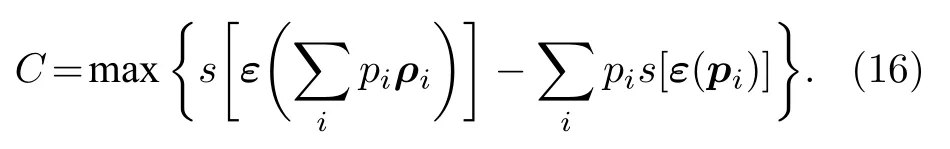
设发送端等概率发射字符 ρ1=|0〉〈0| , ρ2=| 1〉〈1|, 则

对应的诺依曼熵为

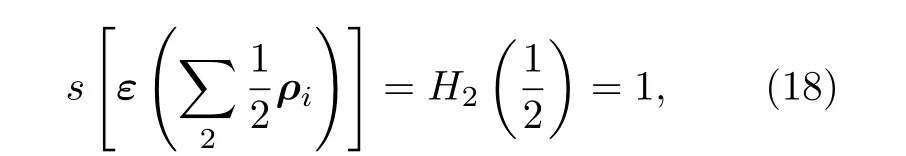
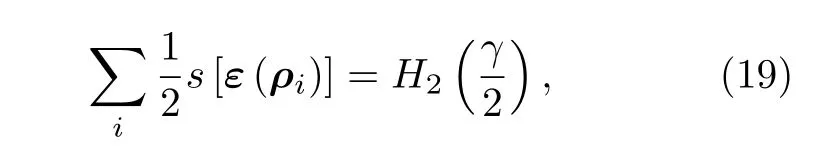
结合(18)式、(19)式, 海洋大气信道的信道容量可以表示为

退极化信道信道容量与风速的关系如图5 所示.图5 中, x 轴为海面风速, y 轴为信道容量.由图5可知, 随着风速增大, 信道容量呈减小趋势.当风速 由 4 m/s 增 大 为 2 0 m/s 时, 信 道 容 量 由0.957减大为0.65.因此, 海面风速对量子通信信道容量影响较大, 可根据风速调整信道带宽, 改善量子通信的通信效果.

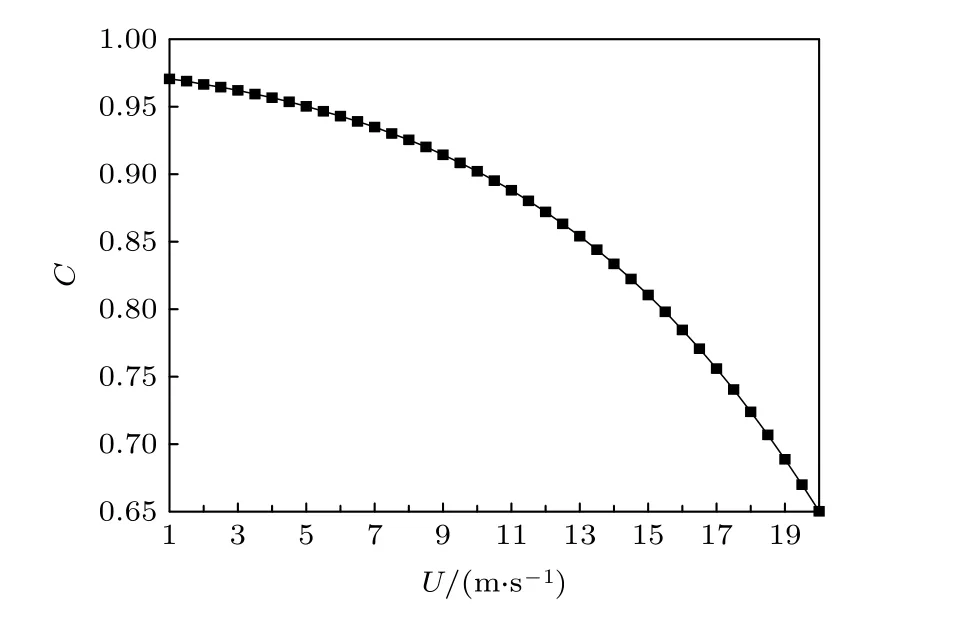
图5 信道容量与风速的关系Fig.5.Relationship between channel capacity and wind speed.

5 风速对信道平均保真度的影响

量子态在海洋大气中传输时, 有一定的概率出现退极化.信道的平均保真度F 可以表示为[22]

设输入字符为 ρ1=|0〉〈0| 、 ρ2=|1〉〈1| , 则:

退极化信道的平均保真度可以表示为

信道平均保真度与风速、信源概率的关系如图6 所示.图6 中, x 轴为海面风速, y 轴为信源字符取 |0〉 的概率, z 轴为信道平均保真度.由图6 可知, 当信源取字符 |0〉 的概率一定时, 随着风速增加,信道平均保真度呈减小趋势.p1取0—0.5 和0.5—1 时, 信道平均保真度呈相互对称的形式.当信源概率小于0.1 或大于0.9 时, 信道保真度随着风速增大急剧减小.当信源概率取0.001, 风速由4m/s 增大为 20 m/s 时, 保真度由0.999 减小到0.974.因此, 风速对退极化信道平均保真度影响较小.

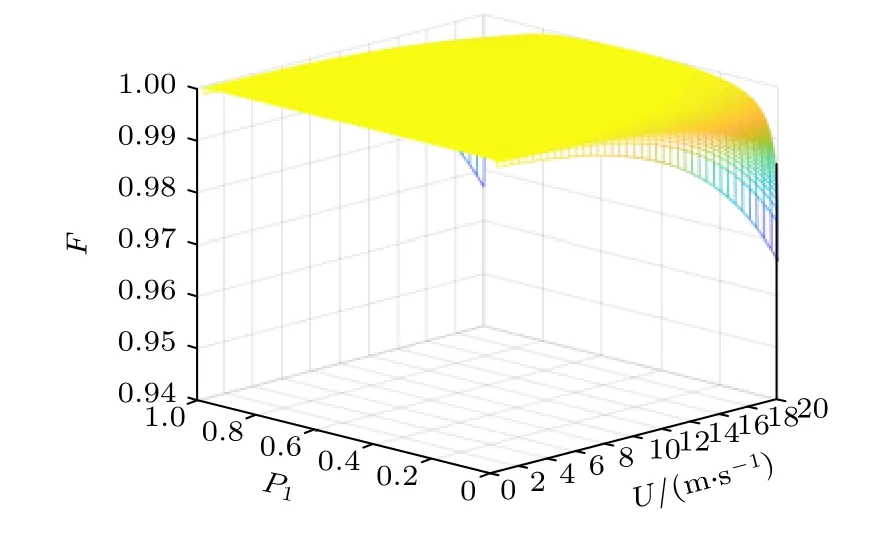
图6 信道平均保真度与风速、信源概率的关系Fig.6.Relationship between channel average fidelity and wind speed、source probability.

6 结 论

本文研究了不同海面风速对海洋上方量子通信信道的影响.根据风速和大气中气溶胶粒子数的对数关系, 拟合了不同风速下海洋大气气溶胶粒子谱分布曲线.以 B B84 协议为例, 分析了风速及传输距离对信道误码率的影响.针对退极化信道, 分析了风速对信道容量和信道平均保真度的影响.仿真结果表明, 随着风速的增加, 量子通信的各项性能指标均受到不同程度的影响.因此在海洋上方量子通信时, 需根据具体的海上天气指数, 调整通信系统参数, 以降低背景噪声对通信性能的影响.