铁芯不闭合的变压器之研究
2021-03-04林辉庆
林辉庆
(杭州市余杭高级中学 浙江 杭州 311100)
1 问题的提出
(2011年高考物理浙江卷第16题)如图1所示,在铁芯上、下分别绕有匝数n1=800和n2=200的两个线圈,上线圈两端与u1=51sin314tV的交流电源相连,将下线圈两端接交流电压表,则交流电压表的读数可能是( )
A.2.0 V B.9.0 V
C.12.7 V D.144.0 V
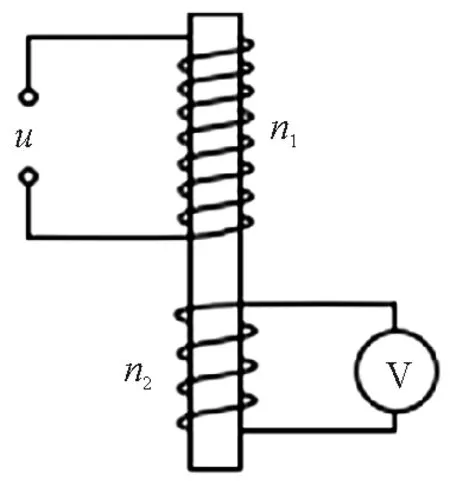
图1 非理想变压器
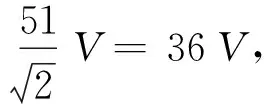
此题被普遍地认为是一道好题,因为它能区分考生是否理解变压器电压比公式的适用条件,能否用它分析有关的实际变压器问题.直到现在,很多学习资料仍选用此题,一些教学论文也引用了此题.但对于此题答案的解释,却存在着悬而未决的争议.一般的解释是,由于漏磁,通过上、下线圈的磁通量关系Φ1>Φ2,所以U2应该小于9 V[1].但质疑者认为,铁芯有增强与聚集磁感线的作用,虽然有漏磁,但不会大到使电压表的读数有2 V与9 V这么大的差异;如果实际的差异真有这么大,那么,可能还有一个原因:这一非理想变压器的原线圈自感较小,感抗也较小,而原线圈有电阻,感抗分得的电压小于输入电压36 V.
2 铁芯不闭合对变压器线圈感抗的影响
2.1 实验现象
如图2所示,将中学教学中使用的可拆变压器的原线圈与交流电流表串联后,接到学生电源的交流输出端,电流表的指针不偏转.而如图3所示使可拆变压器的铁芯不闭合,电流表的指针就有一个偏角.

图2 空载电流等于零

图3 空载电流不等于零
实验表明,变压器的铁芯闭合时,原线圈的自感L和感抗XL可以看作∞,空载电流趋于零;铁芯不闭合时,原线圈的自感L和感抗XL不能看作∞,空载电流不等于零.
2.2 理论解释
铁芯闭合与不闭合,套在铁芯上的线圈的自感L和感抗XL为什么会发生如此大的变化?我们可以在一种理想的情况下从理论上进行探讨.
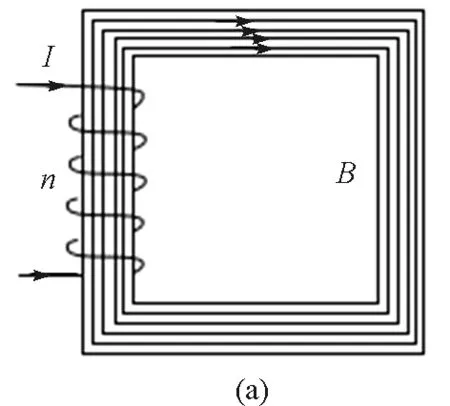
如图4(a)所示,通有电流I的n匝线圈绕在周长为l的闭合铁芯上,磁感线全部集中在铁芯内部,磁感应强度为B;如图4(b)所示,将铁芯截去一小段Δl,磁感线除间隙处,也全部集中在铁芯内部,磁感应强度变为B′.由安培环路定理
∮H·dl=∑I
和磁感应强度与磁场强度的关系
B=μμ0H
对图4(a)、(b)分别得到
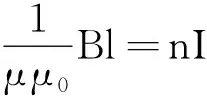
求出
变压器铁芯的磁导率μ可高达10 000[2].量得可拆变压器的l≈36 cm,取Δl=1 cm,μ=8 000,由上式求得
可见,如果铁芯不闭合,哪怕缺口很小,都会使铁芯中的磁感应强度大大减小.因此,绕在不闭合铁芯上的线圈的自感L远小于绕在闭合铁芯上线圈的自感.图1中的铁芯“缺口”更大,原线圈的自感较小,对交流电的感抗也小,因此空载电流较大.
3 原线圈和副线圈电压比的相关因素
设一铁芯不闭合的变压器,原、副线圈的匝数分别为n1和n2,原线圈的电阻为R,感抗为XL.在原线圈两端加交变电压U1,副线圈两端开路或接入理想交流电压表时电压为U2.此种情况下副线圈中没有感应电流,不会在原线圈中产生感应电动势;原线圈中有空载电流I,其中电阻R和感抗XL产生的电压分别为
UR=IRUL=IXL
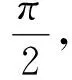
(1)
将UL与U1的比值记为k1,则
(2)
通过原、副线圈的磁通量用Φ1和Φ2表示,则有
令
即可得到
(3)
综合(2)、(3)两式得到
(4)
可见,副线圈与原线圈的电压比等于3个系数的乘积.系数k0是副线圈与原线圈的匝数比,系数k1反映原线圈感抗较小造成UL小于U1的程度,系数k2反映漏磁的程度.k0是电压比的理想值,k1k2反映电压比偏离理想值k0的程度.
4 感抗因素与漏磁因素的测定
4.1 测量原理
从式(2)、(4)可以得到
(5)
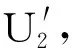
(6)
由式(5)、(6)得到
(7)
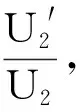
4.2 实验测量
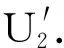

图5 铁芯不闭合的变压器
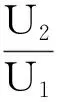
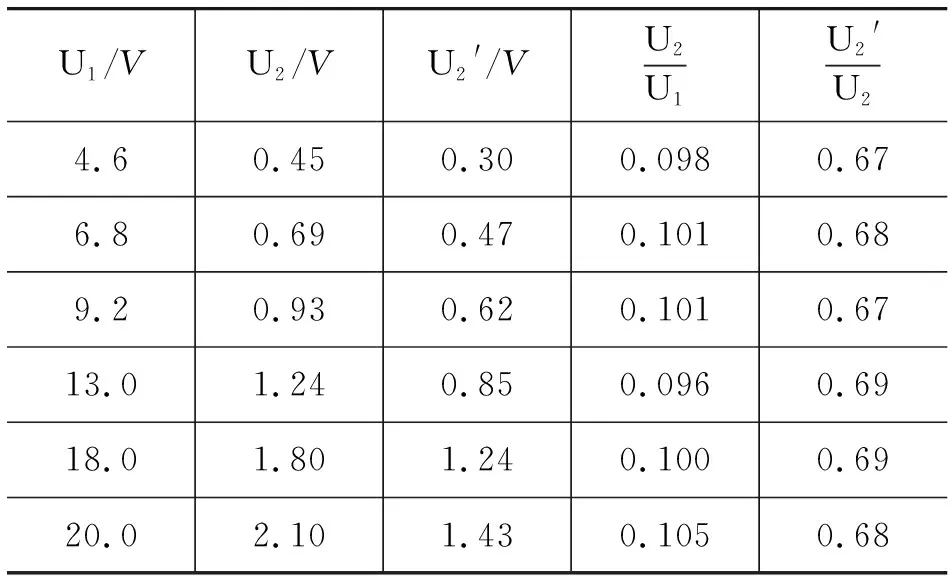
表1 变压器原、副线圈的电压关系
5 结论
实验测出k1=0.93<1,表明原线圈感抗减小确实是铁芯不闭合的变压器副线圈与原线圈的电压比小于理想值的原因之一.至于上述实验情况中,k2
对于图5所示的变压器
k1k2=0.93×0.43=0.40
本文开头试题中的变压器
它虽然比图5情况的k1k2小,但仍是可能的.且不说在这两种情况中线圈与铁芯的有关因素可能不同,单就图1情况铁芯的缺口比图5情况铁芯的缺口大,就会造成它的k1k2变小.
电工使用的钳形电流表实际上是铁芯有缺口、原线圈匝数n1=1的电流互感器(图6).捏紧扳手张开铁芯,使通有交流电的导线穿过铁芯缺口,放开扳手合上铁芯,就能从电流表中读出导线中的电流.放开扳手后活动铁芯与固定铁芯不可能完全密合,它们之间存在着小缺口.各次测量时,两块铁芯的密合程度和通电导线在铁芯回路中的位置不会完全相同,漏磁和线圈自感变小产生的影响也不相同.这导致各次测量时电流表读数与被测电流的比值不会相同,所以钳形电流表只能粗略测量电流.
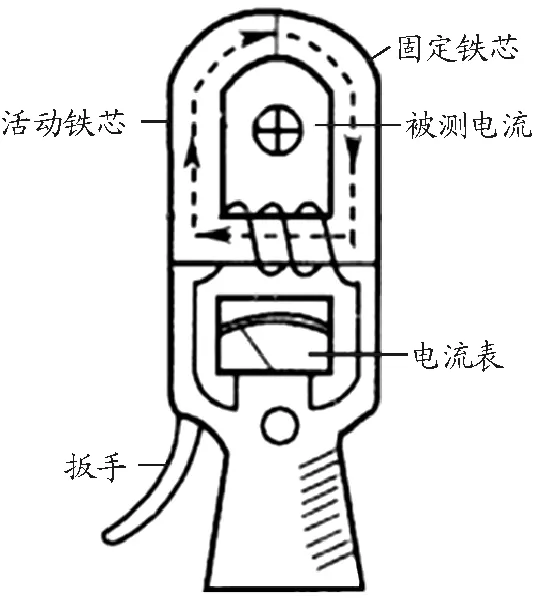
图6 钳形电流表
