双轴跟踪和单轴南北向跟踪CPV/T 系统的热电性能研究
2021-03-04张高明刘志兵王泽昕魏进家
黄 晔,张高明,高 峰,刘志兵,王泽昕,魏进家*
(1. 陕西榆林能源集团有限公司,榆林 719000;2. 西安交通大学动力工程多相流国家重点实验室,西安710049;3. 国家电网山西省电力公司电力科学研究院,太原 030001)
0 引言
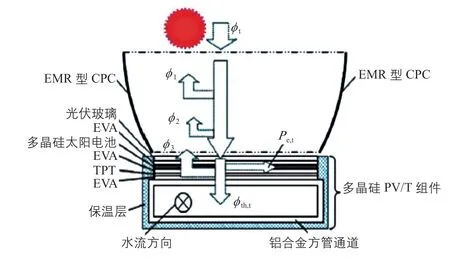
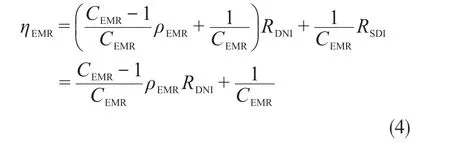
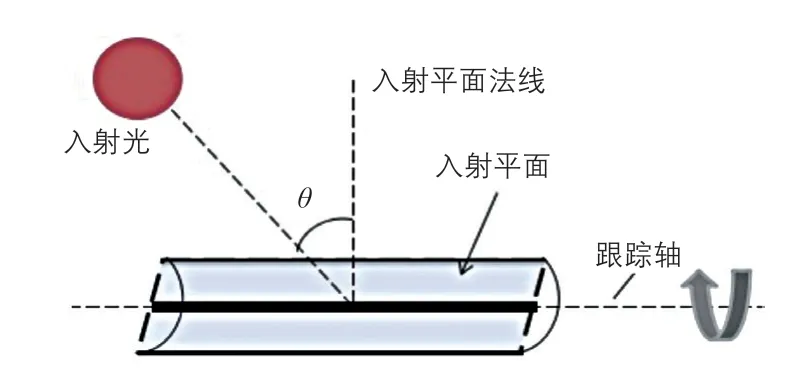
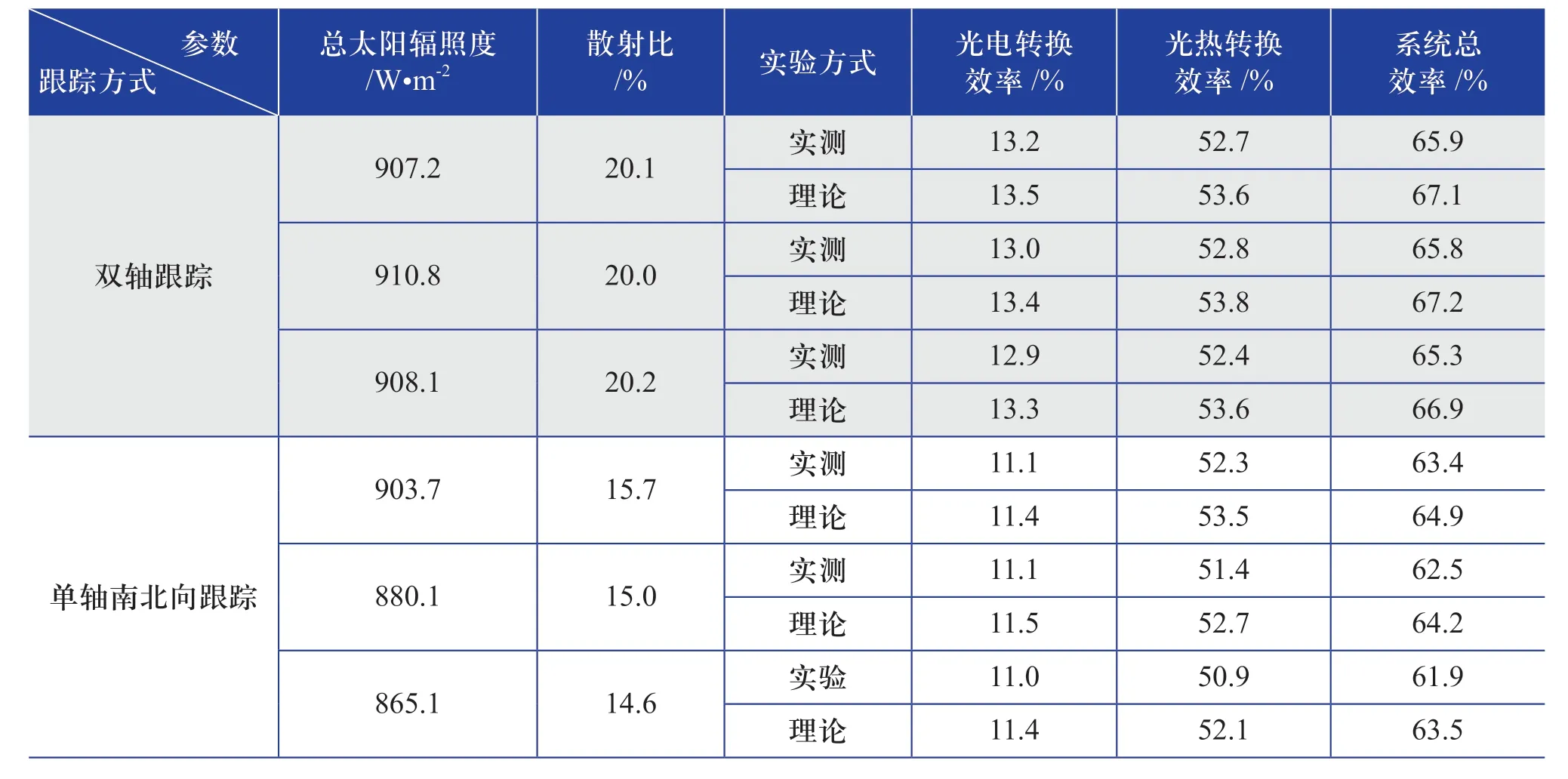
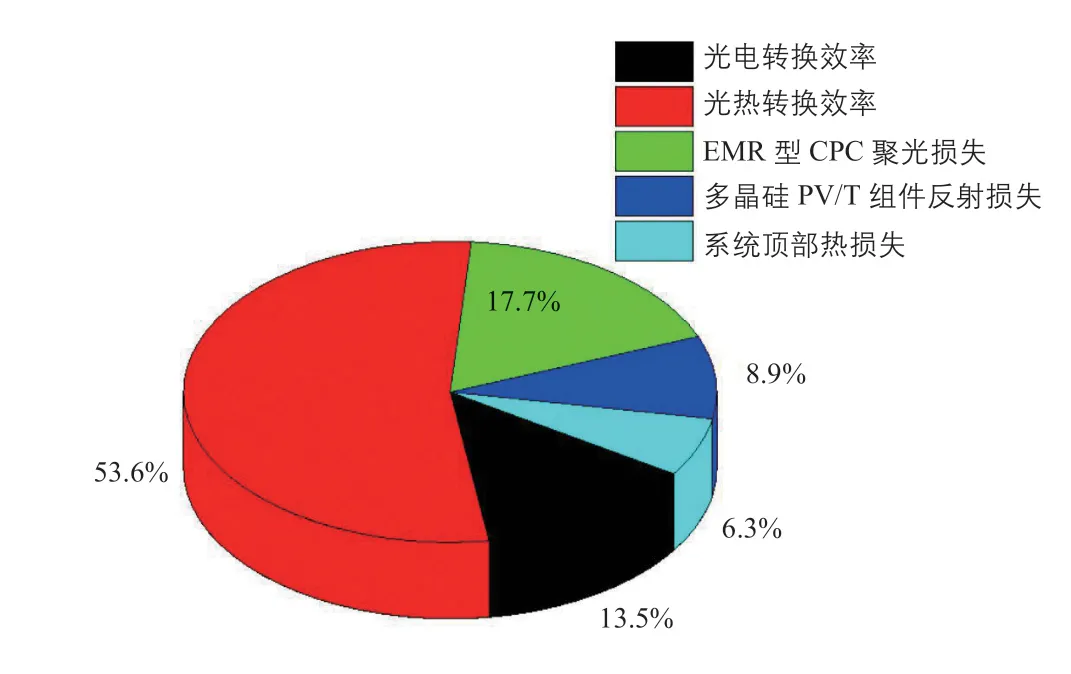
聚光光伏光热(CPV/T)系统是一种新型的太阳能利用技术,由于其可以同时产热和产电,也可以与采暖、制冷、海水淡化及干燥除湿等生产和生活方面常见的应用场合相结合,具有较好的产业化前景。聚光器是CPV/T系统中主要的核心部件之一,根据聚光器几何聚光比C的不同,CPV/T系统可以分为高倍聚光(C≥100)CPV/T系统、中倍聚光(10 对于中倍聚光和高倍聚光CPV/T系统而言,聚光器一般采用成像聚光器,如碟式聚光器[3]和菲涅尔透镜[4]等。成像聚光器对于加工制造精度和跟踪精度均有相当高的要求,而且由于该类聚光器的聚光能量密度太高,需要采用换热能力极强的冷却技术。 而对于低倍聚光CPV/T系统而言,聚光器一般采用非成像聚光器。由于非成像聚光器对于加工制造和跟踪精度的要求均相对较低,而且对于换热的要求也不高,因此在综合考虑投资、运行维护成本和输出性能等方面因素后发现,低倍聚光CPV/T系统更具有应用前景。 目前针对低倍聚光CPV/T系统聚光器的研究主要集中在V形槽式反射镜[5]和复合抛物面聚光器(CPC)[6]等方面。丁超等[5]设计了一种新型的双V形低倍聚光结构,采用铝板贴膜的方式制作反射镜,既减轻了聚光器的重量,又降低了成本;同时还建立了聚光器的数学模型,针对聚光镜的结构尺寸、镜面角度进行了经济性分析,得出了聚光器镜面的最优角度。吴小龙等[7]设计搭建了一种V形槽式低倍CPV/T一体化组件,利用TracePro软件模拟发现,通过动态调整反光铝板的安装角度,在太阳辐射强度最强时,V形槽安装角度在20°~30°之间可以确保该一体化组件整体的聚光效率最高。孙健等[8]设计并搭建了低倍复合抛物面聚光镜CPV/T单通道空气系统实验台,对不同工作环境下CPV/T系统的热、电性能进行了实验研究。结果显示,CPV/T系统的系统效率随太阳辐射强度的增加而增大,系统的最大光电转换效率为11%,最大光热转换效率为70%;最大㶲效率为16%,比单纯发电时的最大㶲效率提高了约5%。PROELL等[9]搭建了一个尺寸为1460 mm×600 mm×150 mm的CPCPV/T系统,并测试了该系统的性能,结果表明,出口水温为107 ℃且系统采用MPPT时,该系统的光热转换效率比尺寸相同的平板PV/T系统的提高了1倍。 由于V形槽式反射镜的设计、制造及装配都较为简单,因此其成为早期低倍聚光CPV/T系统常采用的聚光器之一。但由于V形槽式反射镜的几何聚光比一般都不超过3,导致其不适合用于热流密度需求高的场合。而相比于V形槽式反射镜,在材料消耗可控范围内,复合抛物面聚光镜(CPC)的几何聚光比可以提升到4~10;而且由于CPC拥有较大的采光半角,使其对于跟踪精度的要求较低。 基于上述考虑,本文选用CPC作为CPV/T系统的聚光器,搭建了2套分别采用双轴跟踪和单轴南北向跟踪方式的CPV/T系统实验平台,并测试了采用不同跟踪方式的CPV/T系统的热、电性能。同时从理论上建立了可用于预测采用2种跟踪方式的CPV/T系统热、电性能的模型,并利用理论模型对双轴跟踪CPV/T系统进行了能量衡算,分析了系统的能量损失,并提出了提高系统效率的方法。 本文搭建的分别采用双轴跟踪和单轴南北向跟踪方式的CPV/T系统实验平台的实物图如图1所示。 图1 采用2种跟踪方式的CPV/T系统实验平台实物图Fig. 1 Photo of CPV/T system experimental platform with two tracking modes 不同跟踪方式的实现,需要光学传感器和电机协调运作。双轴跟踪方式采用四象限传感器进行信号探测,通过2台电机在东西向和南北向2个方向进行跟踪;单轴南北向跟踪方式采用二象限传感器进行信号探测,只需要通过1台电机在南北向进行跟踪。 由于传统的CPC高度过高,制造难度和成本均偏高,因此在本CPV/T系统中,采用西安交通大学自主研制的消除多次反射(EMR)型CPC。该EMR型CPC的高度仅为传统CPC的49%,材料消耗降低一半以上,制造成本大幅减少[10]。本CPV/T系统主要由EMR型CPC及多晶硅PV/T组件组成。其中,多晶硅PV/T组件由光伏玻璃、EVA、多晶硅太阳电池、TPT、保温层及铝合金方管通道组成,其结构和能量传输示意图如图2所示。其中,φt为入射的总太阳辐射通量,W;Pe,t为多晶硅太阳电池输出的电功率,W;φth,t为冷却工质回收的热功率,W;φ1为聚光环节损失的太阳辐射通量,W;φ2为多晶硅PV/T组件玻璃盖板反射的太阳辐射通量,W;φ3为多晶硅PV/T组件上表面的热损失,W。 图2 CPV/T系统的结构和能量传输示意图Fig. 2 Schematic diagram of CPV/T system structure and energy transmission 如图2所示,太阳能能量在CPV/T 系统的传输环节包括聚光环节、光伏发电环节及光热利用环节。聚光环节的主要设备为EMR型CPC;光伏发电环节的主要设备为多晶硅太阳电池;光热利用环节的主要设备为冷却工质流经的铝合金方管通道。能量在这些环节的传输与转换过程中,共涉及到7个能量参数,分别为φt、φ1、φ2、φ3、Pe,t、φth,t及多晶硅PV/T组件底部损失的热流量φ4。但由于多晶硅PV/T组件底部采用保温层,能量损失很低,因此可忽略φ4的影响。 简化后的CPV/T系统的能量传输过程共涉及6个能量参数,根据能量守恒定律,可以得到如下关系式: 为了计算得到上述6个能量参数,需要计算相应的气象参数、尺寸参数及热物性参数等。 1)φt的计算。φt可表示为: 式中,Gt为入射的总太阳辐照度,W/m2;Ain,t为CPV/T系统的采光面积,m2。 2)φ1的计算。φ1可表示为: 式中,ηEMR为EMR型CPC的聚光效率。 ηEMR为EMR型CPC聚光平面(即多晶硅PV/T组件表面)接收的总太阳辐射通量与EMR型CPC平面入射的总太阳辐射通量的比值。假设EMR型CPC的几何聚光比为CEMR,入射的总太阳辐照度中太阳直射辐照度的占比为RDNI,太阳散射辐照度的占比为RSDI。对于太阳直射辐照度而言,有1/CEMR的直射光线会不经过聚光镜反射而直接照射在多晶硅PV/T组件上,有(CEMR-1)/CEMR的直射光线会经过反射率为ρEMR的聚光镜一次反射在多晶硅PV/T组件上;而对于太阳散射辐照度而言,聚光效率为其几何聚光比的倒数[11-12]。 因此综上所述,ηEMR可表示为: 将式(2)和式(4)代入式(3),可得到φ1的计算公式为: 3)φ2的计算。φ2可由入射到多晶硅PV/T组件表面的总太阳辐射通量与多晶硅太阳电池吸收的总太阳辐射通量的差值求得。入射到多晶硅PV/T组件表面的总太阳辐射通量即入射到EMR型CPC聚光平面的总太阳辐射通量,而多晶硅太阳电池吸收的总太阳辐射通量需要在此基础上考虑玻璃盖板的透过率τc与多晶硅太阳电池的吸收率αpv。因此,φ2可表示为: 式中,τc取0.92,αpv取0.9。 4)φ3的计算。φ3由玻璃盖板与天空的辐射换热量及玻璃盖板与环境的对流换热量组成。其公式可表示为: 式中,hc-sky为玻璃盖板与天空的辐射换热系数,W/(m2·K) ;S为多晶硅PV/T组件的采光面积,m2;Tc为玻璃盖板的平均温度,K;Tsky为天空温度,K;hc-a为玻璃盖板与环境的对流换热系数,W/(m2·K);Ta为环境温度,K。 其中,Tsky可表示为: hc-sky可表示为[13-14]: 式中,σ为黑体辐射常数,W/(m2·K4),此处取5.67×10-8;εc为玻璃盖板的发射率,此处取0.94。 hc-a可表示为[13-14]: 式中,uwind为环境风速,m/s。 5)Pe,t的计算。Pe,t可表示为: 式中,ηe为实际运行条件下多晶硅太阳电池的光电转换效率。 ηe的计算式可表示为: 式中,γp为太阳电池光电转换效率随温度变化的衰减系数,此处取0.0042;Tpv为实际运行条件下太阳电池的平均温度,K;Tref为标准测试条件(STC)下太阳电池的温度,K,此处取298;ηref为STC下太阳电池的光电转换效率,本文选用多晶硅太阳电池,此处取18%。 6)φth,t的计算。φth,t可由冷却水流经多晶硅PV/T组件时获得的热能计算得到,即: 式中,m为冷却水的质量流率,kg/s;cp为冷却水的定压比热容,J/(kg·K);Tw,in和Tw,out分别为冷却水的进口温度和出口温度,K。 综上所述,将式(2)、式(3)、式(6)、式(7)、式(11)及式(13)代入式(1),整理可得: 由式(14)可以看出,除了Tpv、Tc及Tw,out这3个参数之外,其他变量有的可以由气象参数、物性参数计算得到,有的是系统初始条件,为已知参数。因此要求解Tpv、Tc及Tw,out,还需要引入玻璃盖板的热平衡方程及冷却流体的热平衡方程。 玻璃盖板的热平衡方程即为在稳态条件下,多晶硅太阳电池与玻璃盖板的导热量等于玻璃盖板与环境的辐射换热量和对流换热量之和,即: 式中,hpv-c为多晶硅太阳电池与玻璃盖板之间的导热换热系数,W/(m2·K)。 hpv-c可表示为: 式中,δi为玻璃盖板与多晶硅太阳电池之间的各导热层(玻璃盖板、EVA及多晶硅太阳电池)的厚度,mm,取值分别为3.20、0.30及0.21;λi为玻璃盖板与多晶硅太阳电池之间的各导热层(玻璃盖板、EVA及多晶硅太阳电池)的导热系数,W/(m·K),取值分别为0.7、0.35及148。 冷却流体的热平衡方程即为在稳态条件下,多晶硅太阳电池与冷却流体的换热量等于冷却流体获得的热能。可表示为: 式中,hpv-w为多晶硅太阳电池与冷却流体之间的复合换热系数,W/(m2·K),可由多晶硅太阳电池与冷却流体之间各导热层的热阻及换热器的对流换热热阻之和的倒数求得。hpv-w可表达为: 式中,δj为多晶硅太阳电池与冷却流体之间各导热层(EVA、TPT及铝合方管通流道)的厚度,mm,取值分别为0.3、0.2及2.0;λj为太阳电池与冷却流体之间各导热层(EVA、TPT及铝合金方管通道)的导热系数,W/(m·K),取值分别为0.35、0.614及200;hf为铝合金方管通道上壁面与冷却流体的对流换热系数,W/(m2·K),可由Nu数计算得到。 hf可表示为: 式中,对于本文中的铝合金方管通道内充分发展的层流流动,Nu取8.23[13];λf为冷却流体的导热系数,W/(m·K),此外取0.6;de为本文中的铝合金方管通道的当量直径,m,由流道的长宽尺寸参数计算得到。 最后将式(14)、式(15)及式(17)联立,可得到计算双轴跟踪CPV/T系统性能参数的方程组,即: 对于单轴南北向跟踪CPV/T系统,入射光线一般不与聚光器入射平面垂直,而是与该平面的法线存在一个夹角θ,称为入射角,如图3所示。 对于单轴南北向跟踪CPV/T系统,入射角可由赤纬角和时角计算得到[14],即: 式中,δ为赤纬角,(° );ω为时角(° )。 图3 单轴南北向跟踪方式时的入射角示意图Fig. 3 Schematic diagram of incident angle in north-south single-axis tracking mode 其中,δ可表示为: 令t=2π(N-1)/365,其中N为一年中某一天的顺序数。 ω可表示为: 式中,ST为当地真太阳时。 ST可表示为: 式中,Ts为当地标准时间;Ll为当地地理经度;Lr为标准时间所在地的地理经度;ET为真太阳时与钟表时间之间的时差,可由参数t计算得到。ET可表示为: 对于单轴南北向跟踪CPV/T系统,聚光器入射平面接收到的太阳辐照度与太阳光垂直入射时的太阳辐照度的比值为cosθ,即所谓的余弦效应。由于散射辐射是各项同性的,因此余弦效应实际上只存在于太阳直射辐射。参照计算双轴跟踪CPV/T系统性能参数的方程组,将入射平面接收到的总太阳辐照通量按照余弦效应进行修正,即可得到计算单轴南北向跟踪CPV/T系统热、电性能参数的方程组,即: 从式(25)中可以看出,计算单轴南北向跟踪CPV/T系统性能参数的关键在于求得对应时刻的入射角θ。当θ=0°时,式(25)可简化为计算双轴跟踪CPV/T系统性能的式(20)。 为了验证数学模型的准确性,分别对如图1所示的采用不同跟踪方式时的CPV/T系统的热、电性能进行测试。值得注意的是,为了获得实验平台的稳态运行结果,需确保CPV/T系统的热、电性能均在以下条件下进行测试:CPC入射光孔处太阳直射辐照度每隔15 min的变化幅度小于等于32 W/m2,风速变化幅度小于等于0.8 m/s,环境温度变化幅度小于等于1 ℃。 为了便于将实验测试结果与理论计算结果进行对比,理论计算时的总太阳辐照度、散射比、环境温度、风速、进口水温及流量都与实际测试得到的数据保持一致。双轴跟踪CPV/T系统和单轴南北向跟踪CPV/T系统的理论计算和实际测试分别各进行3次,得到的实验测试结果与理论计算结果对比如表1所示。 表1 双轴跟踪与单轴南北向跟踪CPV/T系统热、电性能的实测值与理论值对比Table 1 Comparison of measured and theoretical value of thermal and electrical properties of CPV/T system with dual-axis tracking and north-south single-axis tracking 由表1可知,采用2种跟踪方式的CPV/T系统的光电转换效率和光热转换效率的实测值与理论值基本吻合;3次测试的理论值与实测值相比,理论模型计算得到的光电转换效率和光热转换效率理论值最大相对误差分别为3.6%和2.5%,均在5%以内。因此,验证了理论模型的准确性。 3次实测结果表明,双轴跟踪CPV/T系统的平均光电转换效率和平均光热转换效率分别为13.0%和52.6%,均高于单轴南北向跟踪CPV/T系统的11.1%和51.5%。虽然测试时双轴跟踪CPV/T系统的散射比略大,但其光热转换效率、光电转换效率仍比单轴南北向跟踪CPV/T系统的光热转换效率、光电转换效率高,这说明余弦效应对单轴南北向跟踪CPV/T系统的热、电性能存在一定的影响。 以双轴跟踪CPV/T系统的第1组计算结果为例,对系统各部分能量进行了衡算,以便分析各部分损失的占比,从而找到需要进一步提升的环节,具体如图4所示。 图4 双轴跟踪CPV/T系统各部分的能量衡算Fig. 4 Energy balance of each part of dual-axis tracking CPV/T system 从图4可以看出,在EMR型CPC聚光损失、多晶硅PV/T组件反射损失及系统顶部热损失这3种损失中,EMR型CPC聚光损失和多晶硅PV/T组件反射损失占据较大比例。因此,为了提高双轴跟踪CPV/T系统的系统总效率,主要在于减少这2部分的损失。减少EMR型CPC聚光损失需提高EMR型CPC的聚光效率,从式(4)可以看出,EMR型CPC聚光效率受几何聚光比、镜面反射率及太阳直射辐照度占比等因素的影响。几何聚光比一般在设计聚光器时就已给定了;而太阳直射辐照度占比受外界气候条件的影响,无法人为控制,因此要提高聚光效率,就只能提高镜面反射率。而要减少多晶硅PV/T组件的反射损失,需要采用透过率高的玻璃盖板,同时可以制作光陷阱结构或采用减反射膜来提高太阳电池的吸收率。 本文针对双轴跟踪和单轴南北向跟踪CPV/T系统的热、电性能进行了研究,得到以下结论: 1)分别搭建了双轴跟踪和单轴南北向跟踪CPV/T系统实验平台,并对系统进行测试,测试结果表明,双轴跟踪CPV/T系统的平均光电转换效率和平均光热转换效率分别为13.0%和52.6%,均高于单轴南北向跟踪CPV/T系统的11.1%和51.5%。 2) 建立了预测采用2种跟踪方式的CPV/T系统热、电性能的理论模型。通过将系统的实测值与理论模型得到的理论值进行比较发现,光电转换效率和光热转换效率理论值与实测值的最大相对误差分别为3.6%和2.5%,均在5%以内,验证了理论模型的准确性。 3) 利用理论模型对双轴跟踪CPV/T系统进行了能量核算,发现EMR型CPC的聚光损失和多晶硅PV/T组件的反射损失是影响系统效率的关键因素,因此可以采用提高镜面反射率、制作光陷阱结构或玻璃表面贴减反射膜等方法来提高系统效率。 但需要说明的是,尽管双轴跟踪CPV/T系统的热、电性能优于单轴南北向跟踪CPV/T系统,但双轴跟踪设备的成本也比单轴南北向跟踪设备的高,因此还需对不同跟踪方式下CPV/T系统的经济性进行研究,从而找到最适合产业化推广的CPV/T系统跟踪方式。1 CPV/T系统实验平台介绍

2 CPV/T系统的热、电性能理论模型
2.1 双轴跟踪CPV/T系统的能量传输方程及其数学模型
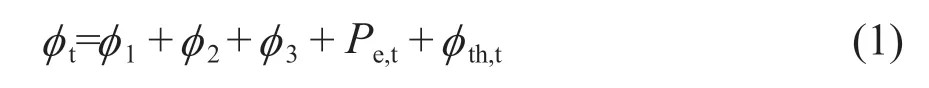


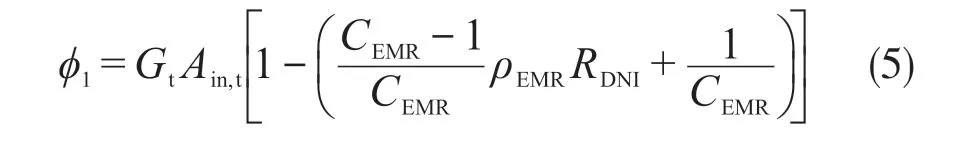

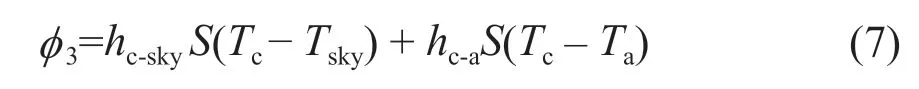




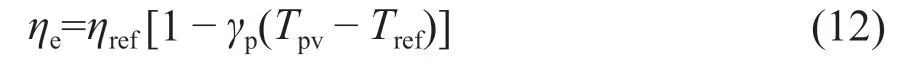

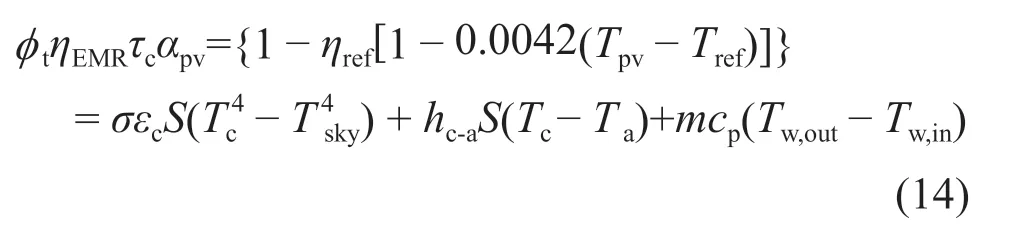
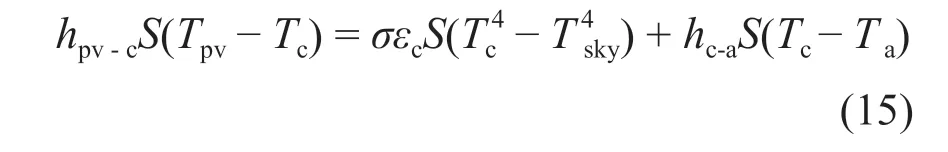

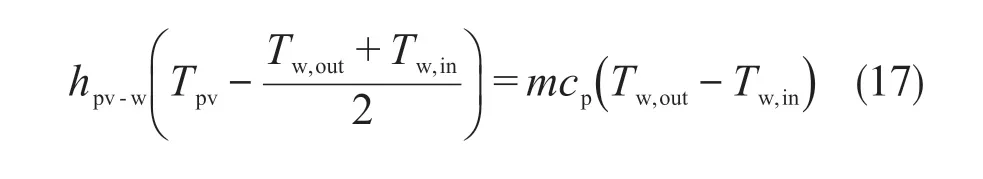
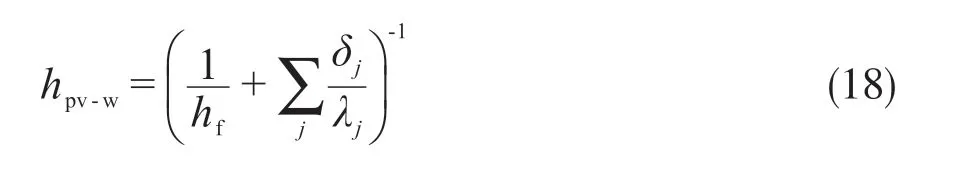

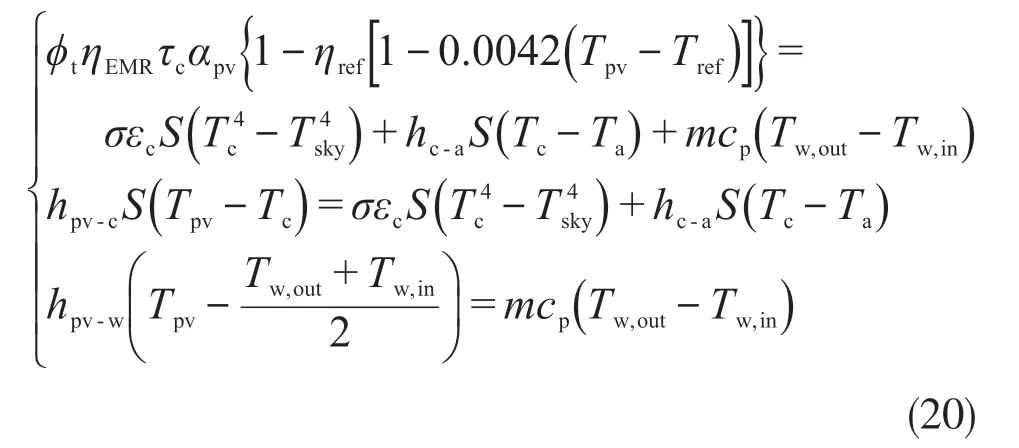
2.2 单轴南北向跟踪CPV/T系统的数学模型
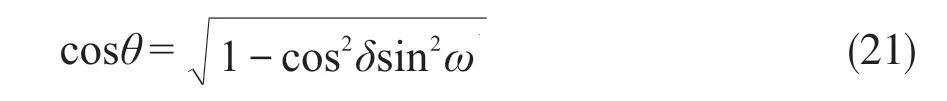

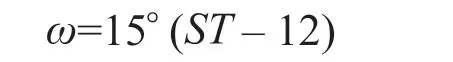
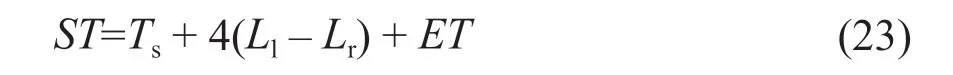
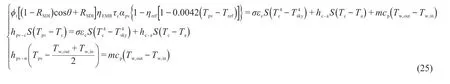
3 结果与讨论
3.1 模型验证
3.2 系统性能影响因素讨论
4 结论
