考虑体应变及干湿循环的黑龙江膨胀土土水特征研究

2021-03-04赵佳敏张爱军牛丽思程旨辉赵双权

西北农林科技大学学报（自然科学版） 2021年1期

赵佳敏，张爱军，牛丽思，于宁，程旨辉，赵双权

(1西北农林科技大学水利与建筑工程学院，陕西杨凌 712100；2黑龙江省水利水电勘测设计研究院，黑龙江哈尔滨 150080)

土水特征曲线(soil water characteristic curve，SWCC)是一种解释非饱和土工程现象及水力特征关系的曲线[1]，可以用来描述非饱和土在持水状态下含水率、体积含水率、饱和度与吸力的对应关系。土水特征曲线研究是非饱和土渗流分析及其本构模型建立的基础，土水特征曲线的测定方法有压力板仪法、滤纸法、张力计法、快速离心机法等，目前针对高吸力范围SWCC的测定普遍采用压力板仪法及离心机法，但压力板仪法试验过程较慢，土样容易产生不同程度的破坏，而离心机法试验过程简单，目前使用最为广泛[2-3]。膨胀土作为一种黏粒含量较高并含有大量亲水性矿物的土，具有对水强敏感、吸水膨胀失水收缩、反复胀缩等一系列特殊性质，是工程界最难对付的特殊土，因此一直是非饱和土理论研究的重点。

目前对膨胀土的研究多集中在其强度、变形、膨胀机理及矿物组成等方面。在膨胀土土水特征研究方面，周葆春等[4]利用脱湿试验探究了湖北荆门膨胀土体变特征与土水特征的相互耦合作用，构建了吸力作用下的体应变方程；邹维列等[5]通过不同初始干密度下的脱湿试验和收缩试验，提出了更为合理的重塑膨胀土体积修正公式；孙德安等[6]基于饱和盐溶液蒸汽平衡法对南阳膨胀土进行了不同干湿循环次数下的土水特征试验，为研究湿胀干缩等性质提供了实测数据；吴珺华等[7]采用滤纸法测量了干湿循环下膨胀土的土水特征曲线，建立了考虑干湿循环效应的SWCC模型；李卓[8]分析了离心机作用下土体干密度变化对SWCC模拟的影响。但上述这些研究均是以特定地区的膨胀土为对象，关于黑龙江膨胀土土水特征的研究还较为鲜见。

黑龙江膨胀土是广泛分布于黑龙江西部和吉林省西北部松嫩平原的一种特殊土，是一种同时具有膨胀性、分散性、冻胀性及高可溶盐含量的湖相沉积软黏土，呈黑褐色或灰褐色，与南方地区的棕红色膨胀土有明显的区别。该类特殊土的存在给该地区的渠道、道路、房屋建设造成了较大的危害，如渠坡滑塌、道路变形和房屋开裂等，严重影响了工程的运行安全，但目前对该类特殊土的土性研究较少，关于其土水特征的相关研究更是鲜有报道。

黑龙江引嫩扩建骨干一期工程是黑龙江尼尔基水利枢纽的配套项目，该工程位于黑龙江省西部嫩江左岸低平原区，是典型的黑龙江膨胀土分布区。本研究以该工程的渠基膨胀土为对象，通过系列试验和分析，建立考虑体应变修正及干湿循环影响的土水特征拟合公式，以期为松嫩平原地区膨胀土土体的渗流研究及其非饱和本构模型的建立提供依据。

1 试验方案

1.1 试验土样的基本性质

供试土样取自黑龙江省引嫩扩建骨干一期工程内的乌南干渠段，取样区位于松嫩低平原中部。地质勘察表明，取样区的地层主要为：(1)第四系全新统河漫滩冲积层冲积级配不良砂、砾石、低液限黏土；(2)上更新统大兴屯组冲湖积低液限黏土、含砂低液限黏土及级配不良细砂；(3)中更新统林甸组冲湖积低液限黏土、高液限黏土、级配不良细砂、中砂、粗砂、砾石。试验土样为第三层中更新统林甸组冲湖积低液限黏土，呈黑褐色，其物理性质指标、化学性质指标与土样的矿物成分见表1～3。

表1 供试黑龙江膨胀土土样的物理指标

表2 供试黑龙江膨胀土土样的化学成分

表3 供试黑龙江膨胀土土样的矿物成分

从黑龙江膨胀土土样的物理化学性质分析结果(表1～3)可以看出，试验所用土样属于低液限黏土，土样中未含有氯离子和钾离子，pH大于8.5，呈强碱性，易溶盐含量大于3 g/kg，从含盐量的角度可以判定其为盐渍土；其自由膨胀率大于30%，判断其属于弱膨胀土。同时通过双比重计试验、碎块试验、针孔试验、孔隙水可溶性阳离子试验、交换性钠离子百分比试验，综合判别该土样为分散性土。由此可以看出，该土样是弱膨胀土，同时也是盐渍土，还具有分散性，是一种极为特殊的膨胀土。

1.2 试样制备

试验所用土样均为重塑样，制备过程如下：(1)土样风干碾压、磨碎后过2 mm筛，测定风干含水率；(2)根据目标含水率及制样所需土样质量计算所需加入的水的质量；(3)将风干后的土样平铺在托盘内，用喷壶均匀喷洒计算好的水量并用勺子搅拌均匀，用保鲜膜密封，静置24 h；(4)静置24 h后测定喷水后的含水率，并计算与目标含水率的误差；(5)根据所需的初始干密度称一定量土样进行制样，其中SWCC试样采用击样法制备，试样体积为100 cm3；收缩试验试样采用压样法制备，试样尺寸为直径61.8 mm×高度20.0 mm。制样过程中，应准确称量环刀及土样质量。

1.3 SWCC试验

SWCC试验采用离心机法进行，本次试验仪器采用日本HITACH公司所产的CR21R高速恒温冷冻离心机，其最高转速为21 000 r/min，最大相对离心力为11 000×g(R11D2转头)，最大容量为250 mL(R14A转头)，工作温度为20 ℃。测定基质吸力的离心机法工作原理是：高速旋转土样产生作用于土样上的离心力，通过离心作用使土样的含水率减小，该离心力就是土样相应的基质吸力[9]，而离心力作用一定时间后土样中的含水率不再变化，此时的含水率就是基质吸力对应的土样含水率。改变旋转速度，即改变离心力的大小，再测定试样在该离心力作用下含水率稳定不变的土样含水率，由此就可以得到土水特征曲线。“每级转速下平衡”的判据就是在离心力作用下土样中的含水率不再发生变化，也就是土样中的水分不再被甩出。试验中用离心时间来控制[10],通过大量试验得到各级基质吸力下土样水分不变时的离心机基质吸力与转速、离心时间之间的关系如表4所示，试验过程中设置离心机运转时间大于表4中规定的离心时间即可保证在每级转速下均能达到平衡。试验中的吸力等级为1，5，10，20，40，60，80，100，200，400，600和800 kPa，试样的初始干密度分别为1.45，1.53，1.58和1.63 g/cm3，共4组。

表4 离心机基质吸力与转速、离心时间的关系

试验操作步骤为：(1)将4种不同初始干密度的土样从保湿缸内取出，试样上下表面各垫滤纸与透水石，并用橡皮筋将试样与透水石上下两端固定，用真空缸进行抽气饱和；(2)将离心管底部多孔板的透水孔对准离心管底部透水孔，称量离心管质量；(3)在土样上部垫上滤纸，环刀刀口朝上装入离心管内，扣盖称质量；(4)按照上一步内所称质量，利用纸片对4个土样进行质量调平，土样管的质量差小于0.5 g；(5)确保离心机转子来回转动灵活，使储水器靠近转子周围的外边缘，土样管透气孔朝上，将土样管放入离心机转头内；(6)拧紧转子上的盖子，关好机壳门，设置转速、时间、温度，运行离心机；(7)在每级转速下达到平衡后，取出土样管，倒掉储水管中甩出的水，称量土样管质量，用电子游标卡尺测量土样直径及高度收缩尺寸，并重新对4个土样进行调平，擦干离心机转子及内壁的水，按上述步骤进行下一级基质吸力试验。

1.4 收缩试验

将与SWCC试样具有相同初始干密度的收缩试样放入收缩仪中进行收缩试验，能够得到不同初始干密度下的收缩曲线，用来修正考虑试样体积变化的SWCC曲线。

1.5 干湿循环试验

对初始干密度为1.45 g/cm3的试样进行0～5次干湿循环。为了尽量使水渗入土中并达到均匀，在试样的增湿过程中，采用胶头滴管对试样上下表面交替反复滴水，一次增湿过程分多次滴加且至少持续24 h，达到控制含水率后用保鲜膜包裹试样再于保湿缸中放置24 h。干燥过程采用烘干法，烘干温度控制为60 ℃，烘干至初始含水率，从而实现干湿循环。之后对干湿循环次数1，3，5次的试样进行离心机SWCC试验[11]。

2 考虑体应变的SWCC修正方法

截至目前，有很多学者根据试验统计的分析方法提出了不同的土水特征曲线模型。本研究选用以体积含水量表示的模型形式，目前常见的有Van Genuchten模型(简称VG模型，1980年)[12]、Fredlund & Xing模型(1994年)[13]、Gardner模型(1958年)[14-15]。其表达式分别为：

VG模型：

(1)

式中：θ为基质吸力s(kPa)对应的土样体积含水率，%；θs为饱和体积含水率，%；θr为残余体积含水率，%；α、q、n均为试验参数，其中n=1-1/q。

Fredlund & Xing模型:

(2)

式中：p、α、m为拟合参数。

Gardner模型：

(3)

式中：α、q为拟合参数。

上述模型均未考虑土样干湿作用下体积变形的影响，由于膨胀土中含有大量的亲水矿物，含水率的变化会使膨胀试样产生湿胀干缩变形，故在进行SWCC试验时，必须考虑体积变化对SWCC曲线的影响，并对其进行修正。本研究采用两种体应变修正方法：其一为基于收缩试验结果的修正方法；其二为基于离心机试验结果的修正方法。同时，对比分析了两种方法对此次试验用土的适用性。

2.1 基于收缩试验结果的修正方法

通过收缩试验结果可以得出线缩率与含水率变化之间的关系。对膨胀土脱湿过程中的体应变，周葆春等[4]直接用SWCC试验前后的体积变化进行修正。其表达式为：

(4)

式中：λV为收缩试验第一阶段的体积收缩系数；ΔV为SWCC试验收缩前后体积的变化值，cm3；V0为试验前试样的初始体积，cm3；Δw为试验结束后试样含水率的变化值，%。

张华等[16]用3个方向的线缩率表示体应变。其表达式为：

(5)

式中：λY为试样的竖向收缩系数，λX为试样的横向收缩系数。

邹维列等[5]根据张华等[16]所得横、竖向收缩系数近似相等的结论，提出膨胀土体积随含水率变化的公式为：

(6)

式中：Z0为试样初始高度，cm；ΔZ为试样收缩高度，cm。

周葆春等[4]采用竖向线缩率代替体缩率，并不能完全反映出膨胀土失水收缩过程中体积收缩的实质。张华等[16]虽考虑了3个方向的线缩率，但实际试验中竖向收缩率可测而横向收缩率量测不准，故也不便于应用。因此，本研究采用邹维列等[5]所提出的方法进行修正。该修正方法为：先采用收缩试验测出土样的收缩系数λY，然后采用式(6)计算体积变化率ΔV/V0，之后采用式(7)～(9)计算对应基质吸力s下修正后的体积含水率θ值，从而可以得到修正后体积含水率与基质吸力的关系。即有：

(7)

(8)

(9)

式中：e、e0为孔隙比和初始孔隙比；Sr为饱和度；Gs为相对密度；w为含水率，%；

2.2 基于离心机试验结果的修正方法

通常情况下，高速离心机SWCC试验不考虑离心过程中试样的压缩，但本次试验土样特殊，土样在离心力的作用下不仅会产生压缩变形，同时随着离心机的高速转动土样含水率逐渐减小，脱湿过程中膨胀土本身也会产生收缩体应变，故离心过程中试样的体应变不可忽视[8]。

本次试验过程中，在每级转速下，待试样水分平衡后测定了试样的收缩量，结果发现，试样横向无明显收缩，故不考虑试样的横向收缩，而只测定试样的竖向收缩。考虑到试验过程中试样的密度变化[17]，利用式(10)、(11)、(12)进行修正。

(10)

式中：ρ′为试样每级平衡后的密度，g/cm3；m′为试样每级平衡后的质量，g。

(11)

式中：ρd为试样每级平衡后的干密度，g/cm3；w′为试样每级平衡后的含水率，%。

由此得到基于离心机试验结果的体积修正后的体积含水率与基质吸力的关系为：

θ=ρdw′。

(12)

3 结果与分析

3.1 收缩试验

收缩试验结果表明，竖向线缩率随试样含水率的变化趋势可以分为线性收缩、过渡收缩及收缩稳定三个阶段。在第一阶段，即线性收缩阶段内，随着土样中孔隙水及空气不断被排出，土样的含水率不断减小，土体颗粒逐渐向中心靠拢，土样逐渐收缩；第二阶段即过渡收缩阶段内，当含水率减小到一定程度后，土体颗粒间的连接已较为紧密，土体的收缩越来越缓慢；第三阶段即收缩稳定阶段，含水率减小引起的土体内应力的变化已很难克服土体颗粒间的相互作用力，土体颗粒间的连接也已趋于稳定，含水率的降低不再引起土样的明显收缩[18-19]。

图1 不同初始干密度下黑龙江膨胀土竖向线缩率与含水率的关系

本次SWCC试验结束后，4个不同初始干密度土样的含水率均大于土样的缩限(20%)，故在进行SWCC试验的过程中，土样均处于收缩试样中的第一阶段，即线性收缩阶段内[5]。同时收缩试验结果(图1)表明，竖向线缩率δsi与含水率的变化(w0-w)可以表示为线性关系，即：

(13)

式中：δsi为竖向线缩率，%；w0为土样试验开始时的初始含水率，%。

通过对不同初始干密度下的黑龙江膨胀土试样进行收缩试验，得到不同的竖向收缩系数如表5所示。

表5 不同初始干密度下黑龙江膨胀土的竖向收缩系数

对试验结果(表5)进行拟合后发现，此次试验所用黑龙江膨胀土试样的竖向收缩系数与初始干密度之间呈线性关系，即初始干密度越大，竖向收缩系数也随之增大。可将其表示为：

λY=Aρd0-B。

(14)

式中：A、B均为试验参数，本次试验中A=0.334，B=0.242 4。

3.2 未考虑体积变化的SWCC

在进行离心试验的过程中，随着基质吸力的增大，土样中的水分及空气不断被排出，土样含水率降低，体积也伴随有一定的收缩。图2及图3为未考虑膨胀土体积变化时，不同初始干密度下分别用含水率w及体积含水率θ表征的SWCC曲线。从图2，3可见，SWCC曲线呈倒“S”型，低基质吸力区土样的失水速率较快，基质吸力对其影响较大，随后土样的失水速率趋于稳定，高基质吸力段土样失水速率降低。同时随着基质吸力的增加，不同初始干密度下的SWCC曲线在低基质吸力区出现一定的交叉，在高基质吸力区有逐渐靠拢的趋势。本次试验的最大基质吸力为800 kPa，当基质吸力达到此值时，4种不同初始干密度试样所对应的含水率分别为22.26%，22.45%，22.87%和21.89%，但仍未达到其残余含水率，由此可以推测不同初始干密度下试样的残余含水率差值不大。同时，从图2，3可以看出，初始干密度越小，其持水能力越差，进气值越小。

3.3 考虑体积变化的SWCC

将利用上述两种方法修正试样体应变后的基质吸力与体积含水率的关系绘于图4中，通过对修正前后结果进行比较，可以得到以下结论：

1)不论是以邹维列等[5]提出的方法修正，还是以考虑离心机作用的方法修正，均可以很明显地看出，在相同的基质吸力条件下，修正后的体积含水率均高于修正前的体积含水率，且基质吸力越高其差别越明显，这是考虑膨胀土体积收缩的结果。

2)对比邹维列等[5]提出的修正方法与考虑离心机作用的修正方法，可以发现低基质吸力区曲线基本重合，高基质吸力区考虑离心机作用的修正方法所得曲线位于邹维列等[5]方法的修正曲线之上。邹维列等[5]提出的修正方法是采用收缩试验量测竖向收缩系数值，并基于张华等[16]的研究结果假定试样的横竖向收缩系数近似相等，计算土样的体应变和体积含水率时，同时考虑了试样在失水收缩过程中横向和竖向体积的变化，计算结果较为精确。而采用游标卡尺直接量测试样每级基质吸力平衡后竖向收缩变形的修正方法，由于打开离心管取出试样时会扰动土样，以及土样表面松散颗粒的影响等，使得量测精度不高。因此后续拟合模型均采用邹维列等[5]的修正方法进行。

3)不论那种修正方法，修正后土样的初始干密度越大进气值越大，持水特性越好。其原因为：初始干密度越大土样越密实，土样内部孔隙较少，在离心力作用下排出的水分越少，土样的通气性及透水性越差。这与张拳[22]、谢舒雷等[23]用滤纸法、压力板仪法等得到的结论相同。

a.邹维列等[5]方法；b.离心机法a.Method of Zou et al[5];b.Method of centrifuge

不同初始干密度下，孔隙比随基质吸力的增加而变化的规律如图5所示。由图5可以看出，不同初始干密度下的孔隙比-基质吸力曲线均未出现交叉现象。初始孔隙比越大的土样，内部大孔隙相对较多，水的通透性越好，对应的体积含水率变化幅度越大，同时随基质吸力的增加孔隙比降幅越明显。土水特征曲线不仅可以反映体积含水率与基质吸力的关系，也可以进一步反映土样内部孔隙的分布情况。初始干密度对土水特征产生的影响，也可以理解为试样内部孔隙发生了不同程度的变化导致的[20]。同时，将不同基质吸力下土样含水率与孔隙比的关系绘制于图6，由图6可见，同一基质吸力下，含水率先增大后减小，含水率随孔隙比的变化规律呈多项式关系。

图5 不同初始干密度下黑龙江膨胀土孔隙比与基质吸力的关系

对同一初始干密度(1.45 g/cm3)不同干湿循环次数下(N=1,3,5)的试验结果进行整理与分析，用体积含水率与基质吸力表示的土水特征曲线如图7所示。图7显示，在初始干密度及含水率均相同的情况下，影响土水特征曲线细观结构的主要原因，一是由于孔隙压缩结构发生了变化；二是土体中所含的易溶盐组成的胶结物在水的作用下被溶蚀，进而使结构发生了变化[21]。由图7可以看出，随着干湿循环次数的增加，试样的饱和体积含水率逐渐增大，但进气值相差不大，在高基质吸力区土水特征曲线有交汇的趋势，说明干湿循环次数不会影响试样的残余体积含水率，但试样的持水性随着干湿循环次数的增加而降低；干湿循环3次和5次的土水特征曲线基本重合，说明随着干湿循环次数的增加，干湿循环所带来的影响逐渐降低，此时试样的结构已逐渐趋于稳定[22-24]。

图7 不同干湿循环次数下黑龙江膨胀土体积含水率与基质吸力的关系

相同初始干密度及含水率下，试样经过不同次数的干湿循环，在吸湿过程中土体吸水膨胀，土样颗粒重新排列，同时由于土样为盐渍土，易溶盐形成的胶结物的溶解也会使土体中的颗粒发生重新排列，溶蚀作用下部分小孔隙连为大孔隙。经过烘干之后，含水率的降低使膨胀土试样发生收缩，吸湿过程中土体颗粒排列所形成的新结构遭到破坏，同时伴随着膨胀土试样的收缩不断产生新的裂隙，随着干湿循环的持续反复进行，试样的裂隙逐渐增多，且无法恢复原样，从而影响其持水性、残余含水率及进气值[6]。

4 SWCC模型拟合及参数分析

4.1 考虑初始孔隙比的SWCC模型拟合

利用Matlab对体应变修正后的试验结果进行拟合，得到Gardner、VG和Fredlund & Xing 3种模型的拟合结果见表6～8。该结果表明，3种模型中Gardner模型参数少，残余体积含水率表现合理，也无百分位以下的参数，最适合于黑龙江地区膨胀土不同初始孔隙比(初始干密度)下基质吸力与体积含水率关系的拟合。而邹维列等[5]试验中所用南水北调河南南阳段的膨胀土更适合用Fredlund & Xing模型进行表征。

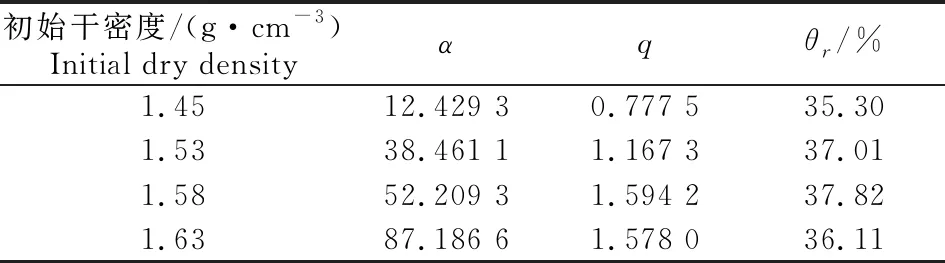
表6 Gardner模型拟合参数

表7 VG模型拟合参数

表8 Fredlund & Xing模型拟合参数

将初始孔隙比与Gardner模型参数绘制于图8。由图8可以看出，初始孔隙比对参数α影响较大，对于q及θr影响较小，且α与初始孔隙比呈线性关系，其随着初始孔隙比的增大而减小；q及θr随初始孔隙比的变化很小，故在模型中取平均值即可[25-26]。

图8 Gardner模型参数与初始孔隙比的关系

将不同初始孔隙比下得到的参数带入Gardner模型并与试验数据进行比较，结果见图9。

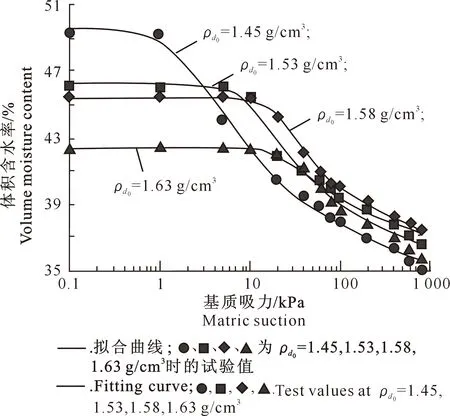
图9 基于Gardner模型拟合的不同初始干密度下的土水特征曲线

将上述参数α与初始孔隙比的线性关系带入Gardner表达式中，可以得到考虑初始孔隙比的黑龙江膨胀土的土水特征曲线模型为：

(15)

式中：c=-344.7，d=303.19，q=1.279，θr=36.562%，θs与初始孔隙比有关。

通过Matlab拟合三维模型，结果见图10。图10显示，初始孔隙比、体积含水率、基质吸力三者相互影响且试验数据点均处于拟合模型面上下，说明该模型拟合效果较好[27-28]。

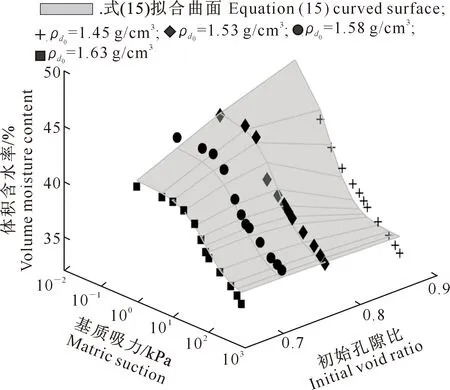
图10 考虑不同初始孔隙比的SWCC模型拟合三维图

4.2 考虑干湿循环次数的SWCC模型拟合

与上述不同初始干密度下土水特征曲线的拟合方法相同，通过对比3种不同模型拟合的结果可以发现，采用Gardner模型能够更好地反映不同干湿循环次数时黑龙江地区膨胀土的土水特性，且R2均大于0.99。考虑干湿循环次数的Gardner模型的拟合参数见表9。为了直观分析干湿循环次数与模型参数的关系，将二者绘制于图11。

表9 考虑干湿循环次数的Gardner模型的拟合参数

图11 Gardner模型参数与干湿循环次数的关系

由图11可知，循环次数N与参数α呈线性关系，但对参数q、θr影响均较小，故可以取其平均值。将3个参数分别带入式(2)，可得到考虑干湿循环次数的黑龙江地区膨胀土的土水特征曲线模型为：

(16)

式中：a=0.047 6，b=19.601，θr=23.028%，q=0.853 4。

将本次试验所得参数代入Gardner公式中绘制拟合曲线，同时与试验结果进行比较，结果见图12。将上述公式拟合于Matlab中，可得到拟合良好的考虑干湿循环次数的土水特征三维图如图13所示。从图12和13可以看出，试验点均位于拟合曲线及曲面上下，说明该模型拟合效果较好。

图12 基于Gardner模型拟合的不同干湿循环次数下黑龙江膨胀土的土水特征曲线

目前，对黑龙江膨胀土的土水特征尚鲜有讨论，将本试验结果与邹维列等[5]利用压力板仪法所得到的试验结果进行比较，可以看出未进行体积修正前，南阳膨胀土与黑龙江膨胀土的含水率与基质吸力曲线表现出相同的趋势，但低基质吸力段的数据点相对较少；体积修正后的SWCC由于考虑了土样脱湿过程中的变形，其饱和含水率更高，说明离心机法可用于研究膨胀土的土水特性。但与黑龙江膨胀土相比，南阳膨胀土的饱和含水率及进气值等均略大。同时，Gardner表达式更适合于黑龙江膨胀土，这也再次佐证了黑龙江膨胀土土水特征研究对黑龙江地区工程建设的必要性。