山区隧道复合式路面结构温度场研究——基于ABAQUS有限元软件数值模拟

杨 斌

(漳州通广云平高速公路有限公司 福建漳州 363000)

0 引言

国内隧道路面结构设计一般直接采用《水泥混凝土路面设计规范》或《沥青路面设计规范》等相关规范条款内容，但实际上隧道内环境温度和隧道外环境温度不同，特别是隧道进口段温度变化复杂，因此将隧道外路面温度状况的研究结果用于隧道路面设计是不合理的。调查表明隧道进出口段路面使用寿命较短，过早出现病害，容易造成安全隐患[1]。

国内对公路隧道温度场的研究较多，且主要针对寒冷地区的公路隧道内空气温度和围岩温度变化规律展开研究。如：王余富通过隧道内环境温度测试和有限元分析，总结了隧道内环境温度的变化特点，为隧道路面温度场的模拟提供理论依据[2]；陈建勋对隧道拱顶、拱腰、边墙和路面4个部位进行长期测试、分析，揭示了隧道温度场的变化规律[3]；韩星等人运用传热学的基本理论对隧道内温度分布进行预测，为隧道内的通风设计提供依据[4-6]。但是，对于公路隧道路面温度场的相关研究较少，且主要针对路面结构深度的温度变化规律进行研究。如：史小丽利用有限元方法对隧道路面结构温度场模拟，结果表明长隧道路面结构温度梯度一天中无明显变化[7]；王瑜采用有限元方法对隧道进出口典型路面结构进行三维建模，分析了不同季节的温度和纵向温度分布趋势，提出温度纵向非稳定段的确定方法[1]。

鉴于此，本文以福建某山区隧道工程项目为例，运用ABAQUS有限元软件对隧道的进口段进行数值模拟，以研究其温度变化规律，为隧道内路面结构设计提供一定的理论参考。

1 基本原理

1.1 基本假设

本研究将隧道内路面结构视为层状结构体系，主要分析的是隧道内复合式路面结构的温度场，其温度场的空间位置分布为三维空间分布，所以对路面结构作出以下3个假设：

(1)路面各层均为完全均匀和各项同性的连续体；

(2)温度变化不随水平坐标的变化而变化，只与厚度有关；

(3)路面各结构层接触良好，热传导连续。

1.2 导热微分方程

在一定的初始条件和边界条件下，根据路面温度场导热方程，可以计算出路面结构任意时刻、任意位置的温度。在传热学中，傅里叶基本导热定律揭示了热流密度与温度梯度的关系，并结合能量守恒定律得出了非稳态热传导三维微分方程[8]，该方程表达式如式(1)：

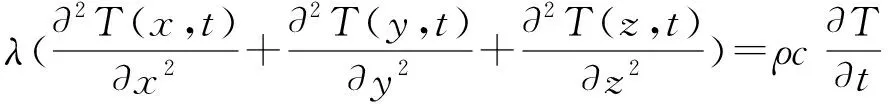
(1)

式中：λ为导热系数(W/m2·K)；

T为瞬态温度(℃)；

ρ为密度(kg/m3)；

c为比热容(J/kg·℃)；

t为时间(s)。

复合式路面结构为多层结构体系，各层路面材料的热力学参数不同，路面各层层间接触条件良好，层间边界上的温度与热流密度连续。故，第i层的导热微分方程和层间接触条件如式(2)～(4)：

(2)

Ti=Ti+1

(3)

(4)

2 模型建立

2.1 计算模型

本研究基于某山区隧道工程项目实例，采用有限元软件ABAQUS进行数值建模，单元类型采用八结点线性传热六面体单元(DC3D8)。有限元计算模型如图1所示，具体尺寸如下：

(1)隧道横断面上，每个尺寸采用1∶1比例建模，初期支护和二次衬砌总厚度为70 cm。围岩宽度设为20 m，长度为20 m。

(2)隧道纵向，采用1∶10比例建模，实际纵向长度为100 m，有限元模型为10 m。

图1 隧道复合式路面有限元模型

2.2 材料参数

表1为隧道内复合式各路面结构层材料参数。

表1 路面结构层材料参数

2.3 温度场边界条件

根据热力学理论，热能传递有传导、对流、辐射3种形式。由于隧道内为封闭环境，路面没有受到太阳辐射，故，本研究只考虑空气对流换热边界条件。

本研究主要研究隧道复合式路面纵向(行车方向)各路面结构层温度分布情况，洞内空气温度按纵向不同位置横断面的日平均空气温度年变化情况进行确定；将监测的洞内空气温度数据统计后，采用正弦函数对日均气温年变化过程进行函数拟合[1]，函数表达式如式(5)：

(5)

式中：i为不同位置横断面；

T0为年平均温度(℃)；

A为日平均温度年振幅(℃)；

t为时间，一个单位为10d；

φ为相位差。

沥青面层与大气的对流换热系数he受到风速vw的影响，本文中的风速采用隧道内的设计风速vw=1.6m/s，对流换热系数与风速的关系和任意时刻下的空气与路表的对流换热关系如式(6)～(7)：

he=3.7vw+0.94

(6)

qh=he(Ta-Tp)

(7)

式中：vw为风速(m/s)；

he为对流换热系数；

qh为对流换热；

Ta为隧道内空气温度(℃)；

Tp为隧道内路表温度(℃)。

3 路面温度场分布特性

3.1 温度的纵向分布变化

(1)夏季阶段

夏季最高日平均温度下，隧道复合式路面结构的温度纵向分布云图如图2所示。

图2 夏季日均温度纵向分布云图

由图2可知，隧道内路面各结构层温度的纵向变化趋向与路表基本一致，不同结构层温度随着路面结构层深度的增加而降低。各路面结构层温度的纵向分布数据如图3所示。

图3 夏季日均温度纵向温度场

由图3可知，隧道各结构层从洞口到洞内10 m处，温度小幅度升高，然后直线下降到40 m处，40 m～100 m洞内路面结构温度纵向变化趋于稳定，路表温度基本保持在28.1℃。不同结构深度的最高温差分别为2.32℃、2.19℃、2.06℃、1.96℃、1.84℃，温差随着路面结构深度的增加而降低，但变化不大。

(2)冬季阶段

冬季最低日平均温度下，隧道复合式路面结构温度纵向分布云图如图4所示。

图4 冬季日均温度纵向分布云图

由图4可知，隧道内路面各结构层温度的纵向变化趋向与路表基本一致，温度随着纵向距离的增加而升高，且温度随着路面结构层深度的增加而升高。

冬季最低温时，各路面结构层温度的纵向分布数据如图5所示。

图5 冬季日均温度纵向温度场

由图5可知，从洞口到洞内30 m段，各结构层温度直线上升，幅度剧烈；洞内30 m到100 m处隧道内，路面结构层纵向温度变化逐渐趋于稳定，温度基本保持在15.5℃。不同结构深度的最高温差分别为1.20℃、1.13℃、1.05℃、0.97℃、0.88℃，温差随着路面结构深度的增加而降低，与路表距离越近，温度变化越大。

3.2 温度梯度的纵向变化

(1)夏季阶段

夏季最高日平均温度下隧道复合式路面结构温度梯度纵向分布如图6所示。

图6 夏季日均温度梯度纵向分布

由图6可知，各结构层温度梯度在洞口0 m到洞内40 m处有所波动，洞内30 m到100 m处纵向温度梯度变化趋于稳定，变化很小。路表温度梯度从洞口上升到洞内16 m处，温度最大值达到7.54 ℃/m，然后直线下降到洞内20 m处，温度最小值为0.93 ℃/m，最后直线升高到洞内24 m处，趋于稳定，基本没有变化。其他结构层的温度梯度变化趋势与路表基本一致。沥青结构层中，随着结构深度的增加，温度梯度升高，且沥青层温度梯度变化较为激烈；沥青层以下的混凝土路面结构层，随着结构深度的增加，温度梯度的波动和最大温度梯度值越来越大，但是基层混凝土板温度梯度值最高，但仍小于沥青层。

(2)冬季阶段

冬季最低日平均温度下，隧道复合式路面结构温度梯度纵向分布如图7所示。

图7 冬季日均温度梯度纵向分布

由图7可知，各结构层温度梯度在洞口0 m到洞内40 m处变化较大，洞内40 m到100 m处纵向温度梯度逐渐趋于稳定，变化较小。路表温度梯度从洞口处下降在洞内6 m处达到最小值-4.06 ℃/m，然后直线上升到洞内8 m处达到最大值-0.78 ℃/m，之后又下降、上升、下降到洞内40 m后逐渐趋于稳定，各结构层温度梯度稳定段的温度梯度差距较小。混凝土结构层中温度梯度小幅上升至20 m后逐渐趋于一条直线。沥青混凝土结构层中，随着结构深度的增加温度梯度下降，且沥青层温度梯度变化较为剧烈；沥青层以下混凝土路面结构层，温度梯度随着结构深度的增加，温度梯度的波幅和最大温度梯度越来越小，沥青层温度梯度稳定段的温度梯度小于混凝土结构层。

4 结论

本文利用ABAQUS有限元软件，结合工程实例和采用实际监测的气象数据，确定隧道路面温度场的边界条件，对隧道复合式路面结构的温度场展开研究，结论如下：

(1)在夏季阶段，隧道洞口到洞内40 m路面，纵向日均温度变化较大，温度先小幅度升高然后急剧下降，洞内40 m后路面结构层温度趋于稳定且基本为一条直线。在冬季阶段，隧道洞口到洞内30 m处，温度急剧上升，然后趋于稳定。

(2)夏季和冬季日均温度梯度，纵向分布在洞口到洞口40 m处变化较大，洞内40 m后路面结构层温度梯度变化趋于稳定。夏季隧道洞口温度梯度变化段，温度梯度先升高后降低；冬季，温度梯度先降低后升高。

(3)复合式路面，夏季各结构层温度随结构深度增加而降低，且温度梯度随着结构深度增加而升高，但沥青面层温度梯度大于混凝土结构层；冬季则呈现相反趋势。

(4)隧道进口段路面结构，日均温度及温度梯度纵向分布与洞口及洞内路面结构层温度梯度的复杂变化情况表明，隧道路面的结构及材料设计与选择应该与一般路面有所不同；对已经投入使用但未出现病害的隧道路面，可以对进口段路面结构采取预防性养护措施。