深基坑混凝土支撑轴力数值模拟与理论计算分析——基于现场监测

韩超超

(健研检测集团有限公司 福建厦门 361199)

0 引言

随着城市地下空间开发利用程度不断提高，房建、市政等多领域涌现出大量不同规模的深基坑工程[1]。钢筋混凝土支撑作为常用的深基坑工程支护型式，其应力状态和变形情况是影响基坑侧壁稳定性的关键因素。深基坑混凝土支撑轴力实测值远超过设计值是工程监测的常态，但支撑结构本身并未出现开裂、变形等异常现象，从而无法准确掌握支撑真实受力情况[2]，这不仅影响判定基坑所处的状况，提高施工风险，也对支撑轴力监测失去实质意义。因此，准确掌握深基坑混凝土支撑轴力是基坑施工中亟待解决的技术难题。

针对混凝土支撑轴力监测值异常分析方法中，主要有理论模型修正法和数值模拟试验法两类。对于理论模型修正法，多位专家学者围绕混凝土收缩徐变、环境温度、配筋率等不同方向开展研究，其中，混凝土收缩徐变是导致轴力异常的主要因素[3-5]。在国内外混凝土收缩徐变研究领域，多位专家学者基于实验数据和经验公式，提出了多个混凝土收缩徐变预测模型。其中，国内主要有建科院(1986)模型和公路桥涵规范(JTG D62-2004)提出的收缩徐变预测模型(以下简称D62)；国外主要有CEB-FIP(1990)(以下简称FIP90)、RILEM B3(1995)(以下简称B3)和GL2000模型[6]。上述国内外混凝土收缩徐变预测模型中，各模型考虑因素和数学表达式不尽相同,如:FIP90模型在考虑混凝土龄期、环境湿度和构件体表比的基础上，还考虑了环境温度和混凝土28d弹性模量；B3模型除考虑常规影响因素外，还考虑了混凝土水灰比、含水量及骨料-水泥重量比等混凝土材料特性对收缩徐变的影响。综合分析现有文献资料发现，现有的大部分混凝土收缩徐变模型具有计算方法简便的特点，但由于各模型所考虑的侧重点不同，也导致计算结果差异明显，这便使得工程技术人员无法准确选择合理的模型开展混凝土支撑轴力计算。数值模拟方法在岩土体物理力学参数、本构模型和网格划分精度合理的前提下，其计算结果往往能较为真实地反映岩土工程实际情况，因此在岩土工程界得到广泛应用[7]。国内外多位专家学者利用不同数值模拟软件，对深基坑开挖全过程或某施工阶段进行了数值模拟试验，并根据模拟结果对混凝土支撑轴力进行分析，并也取得了一定成果[8-9]。但数值模拟方法具有部分岩土体物理力学参数难确定、复杂工程建模困难、模型对计算机性能依赖性强等不足，阻碍了其在实际工程中进一步推广应用。

基此，本文立足某深基坑工程现场监测实际，分析混凝土支撑轴力实测值随监测时间的变化趋势，采用3种不同的混凝土收缩徐变模型对实测轴力数据进行修正，而后利用三维数值模拟软件对深基坑开挖全过程开展数值模拟试验，分析其轴力修正值和模拟值的数值关系。

1 工程概况

1.1 项目概况及地层条件

案例工程位于厦门市集美区禾山村，地下5层，占地面积约为9200 m2，开挖深度41.8 m，基坑水平轮廓尺寸为长×宽=32.73 m×21.70 m。工程前期地质勘察揭露的岩土层由上至下为素填土、残积砂质黏性土、全风化花岗岩、散体状中风化花岗岩、碎裂状中风化花岗岩和中风化花岗岩，各层岩土体体物理力学参数详见表1。

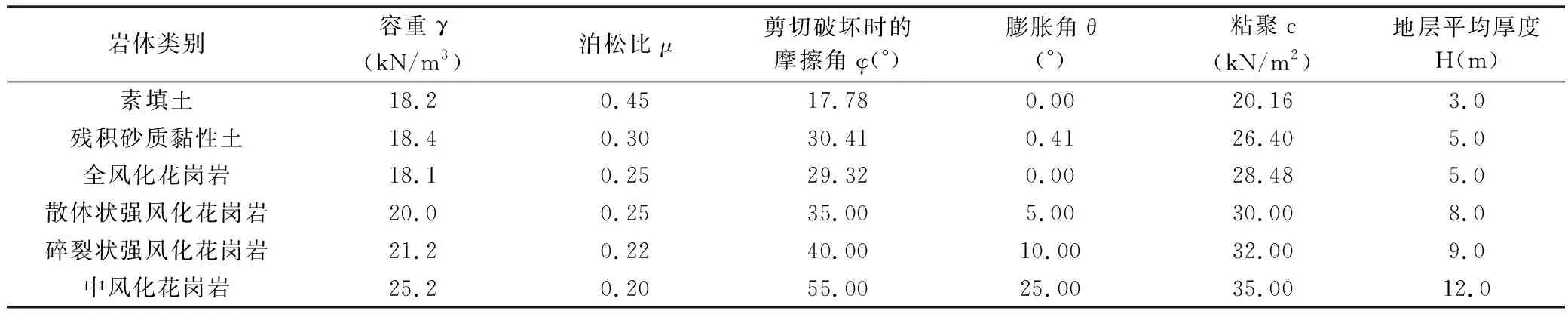
表1 岩土体物理力学参数

1.2 深基坑概况

基坑开挖深度41.8 m，基坑边长×宽=32.73 m×21.7 m，主体围护结构采用灌注桩+内支撑体系，灌注桩尺寸为1200@1400 mm。基坑共采用5道钢筋混凝土支撑，第一道支撑尺寸为800 mm×800 mm，冠梁尺寸2500 mm×1000 mm；第二、三和四道支撑尺寸1000 mm×1000 mm，第一、二道腰梁尺寸1600 mm×1000 mm，第三道腰梁尺寸1800 mm×1000 mm；第五道支撑尺寸1200 mm×1200 mm，第四道腰梁尺寸2100 mm×1000 mm。第一至第四道支撑支撑平均间距均7.0 m，第四至五道支撑间距6.5 m，第五道支撑距坑底13.2 m。灌注桩间采用800@1400三重管高压旋喷桩与灌注桩咬合止水，旋喷桩施作于素填土、残积砂质黏性土、全风化花岗岩和散体状中风化花岗岩面及以下至坑底。基坑围护结构体系剖面如图1所示。

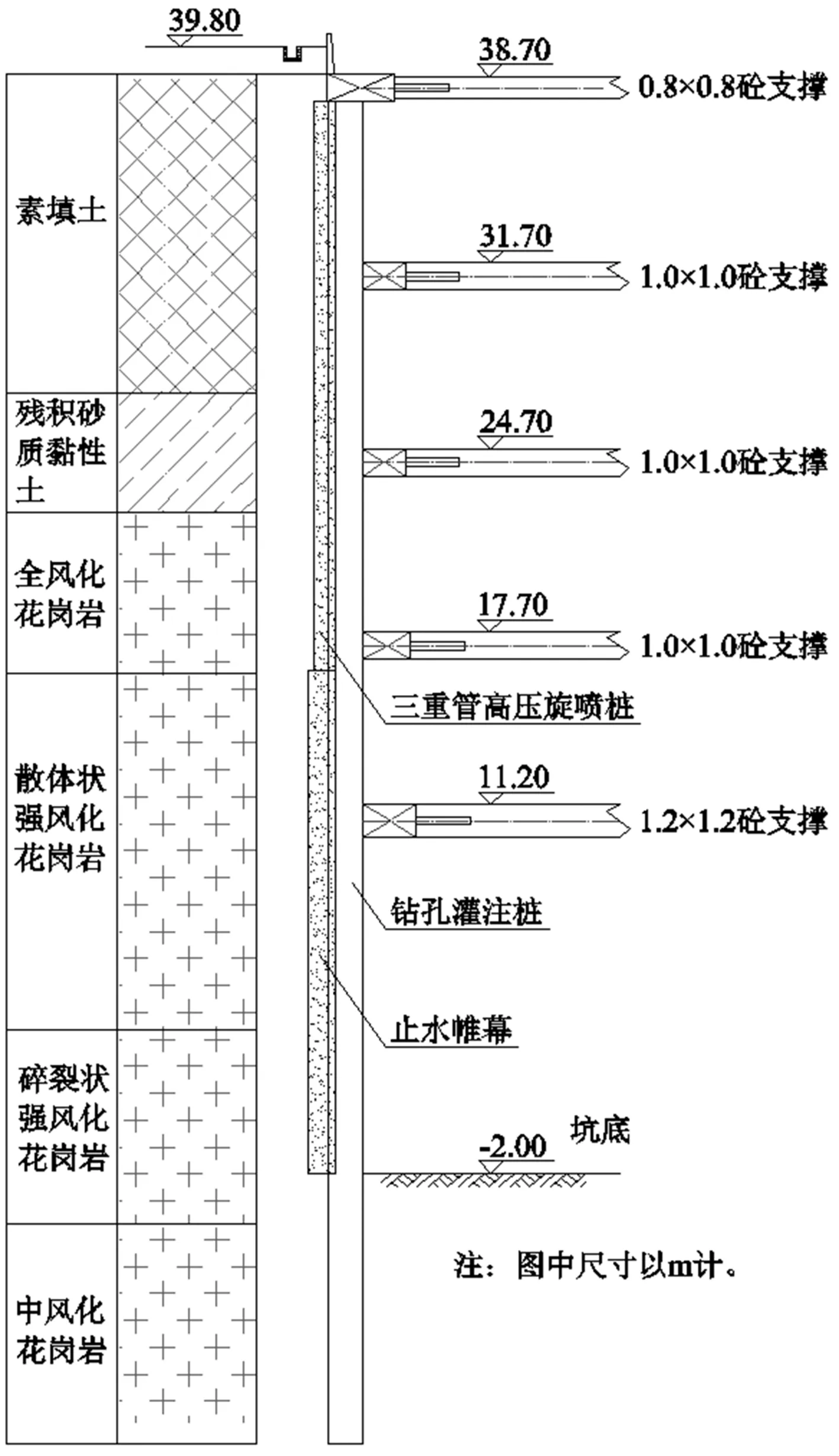
图1 深基坑支护结构剖面图

2 混凝土支撑轴力实测数据及模型修正对比分析

2.1 轴力监测点布设

根据设计及规范文件要求，深基坑混凝土支撑轴力监测点布设位置如图2所示。各道混凝土支撑相应位置监测点在竖向方向位于同一立面。

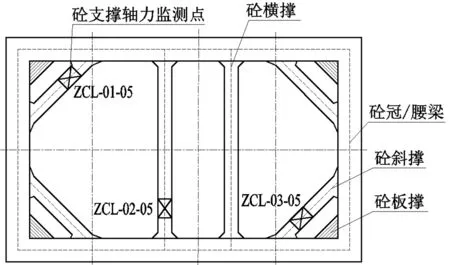
图2 第一至五道混凝土支撑轴力监测点布设图

2.2 监测数据分析

为分析混凝土支撑轴力在一定监测周期内的变化趋势，本研究选取第五道支撑作为研究对象，分析其轴力监测值随监测时间的变化情况。数据统计结果如图3～图5所示。由图3～图5分析可知，在1年的监测周期内，轴力监测值随监测时间的增加整体呈先增加后逐渐稳定的趋势。进一步分析可知，第五道支撑于2018年4月10日施工完成，而后于4月25日开始从第五道支撑平面向下开挖，2018年5月10日至25日监测时间段内， 基坑开挖深度由31.5 m增加到34.6 m，在此期间，第五道3个轴力监测值陆续超过监测预警值(10 500 kN)；2018年7月10日之后，3个轴力监测实测值陆续超过C35混凝土极限抗压承载力(24 000 kN)，且具有持续缓慢增长趋势。从图表数据可知，截止2019年4月24日，支撑轴力实测值已达到35 000 kN，这是非常不合理的。经过持续的现场巡视和其他监测内容(如深层水平位移)获取的数据佐证，各支撑表面无开裂、变形等异常现象，各监测项目在监测后期均未超过预警值且数据趋于稳定。因此，现有支撑轴力监测值计算中包含了收缩、徐变等多种复杂因素的影响，在文章后续内容中，笔者拟采用现有的一些经典理论模型对监测值进行修正，并通过数值模拟来对比论证。

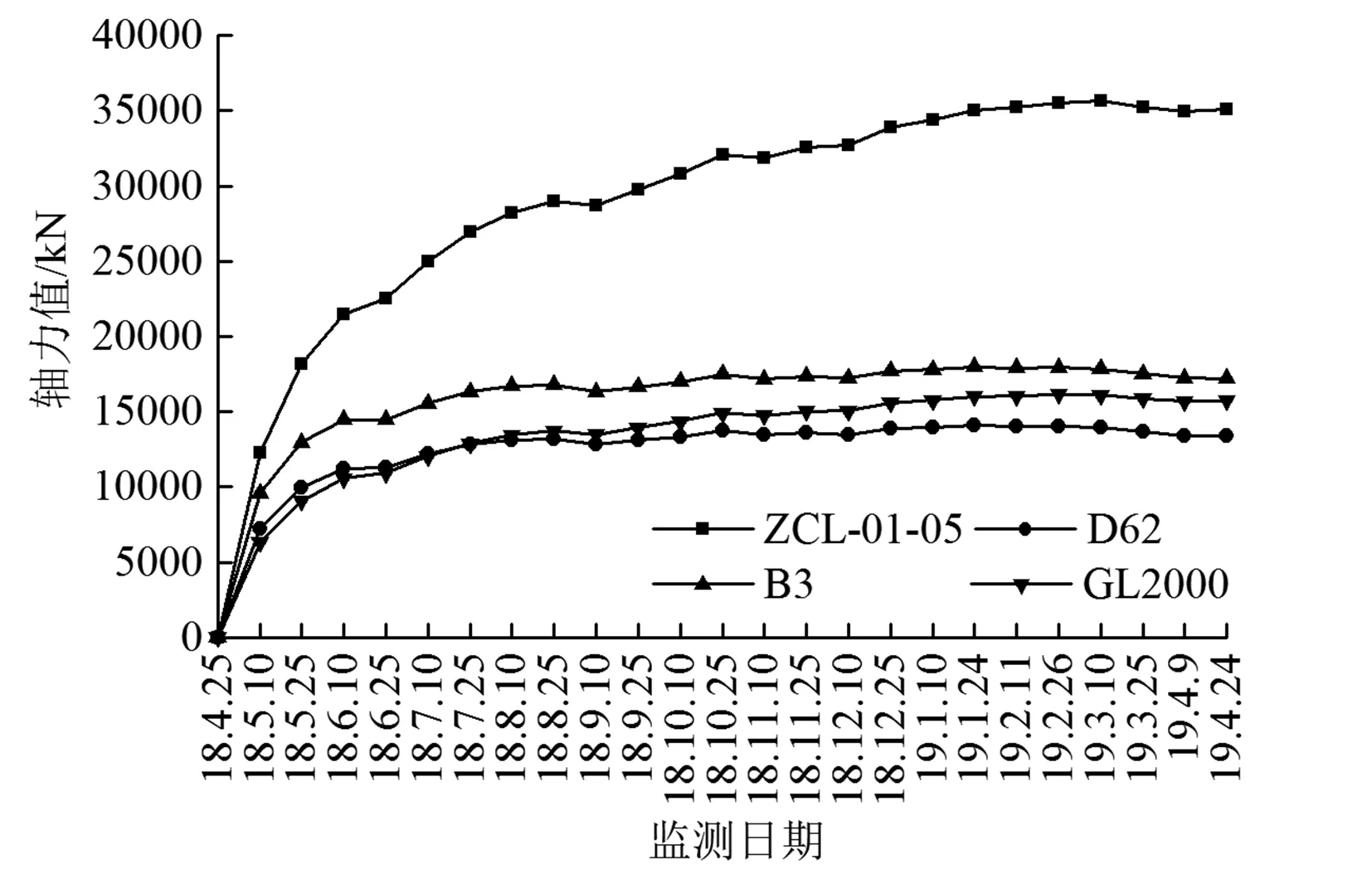
图3 ZCL-01-05监测点轴力实测值与理论修正值对比曲线

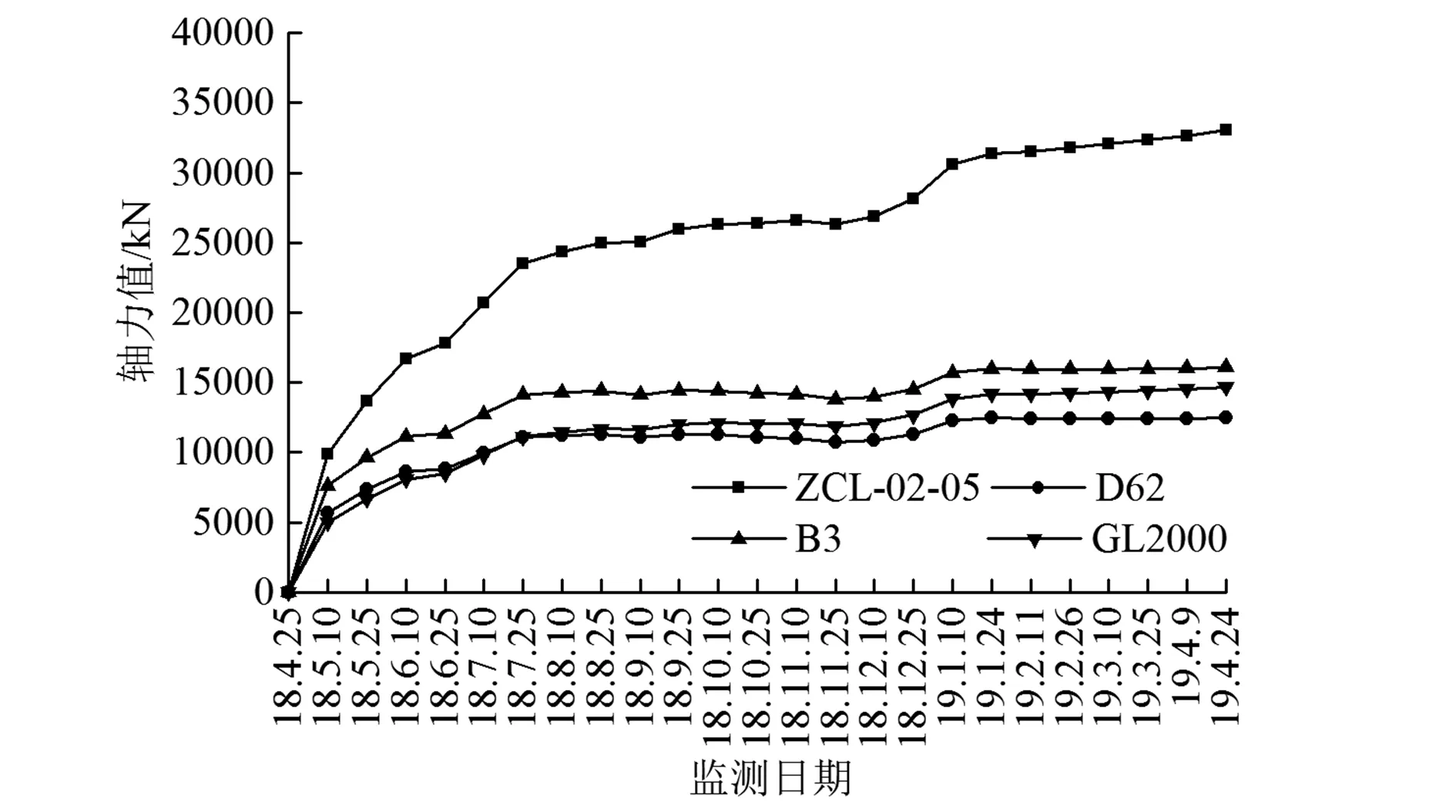
图4 ZCL-03-05监测点轴力实测值与理论修正值对比曲线

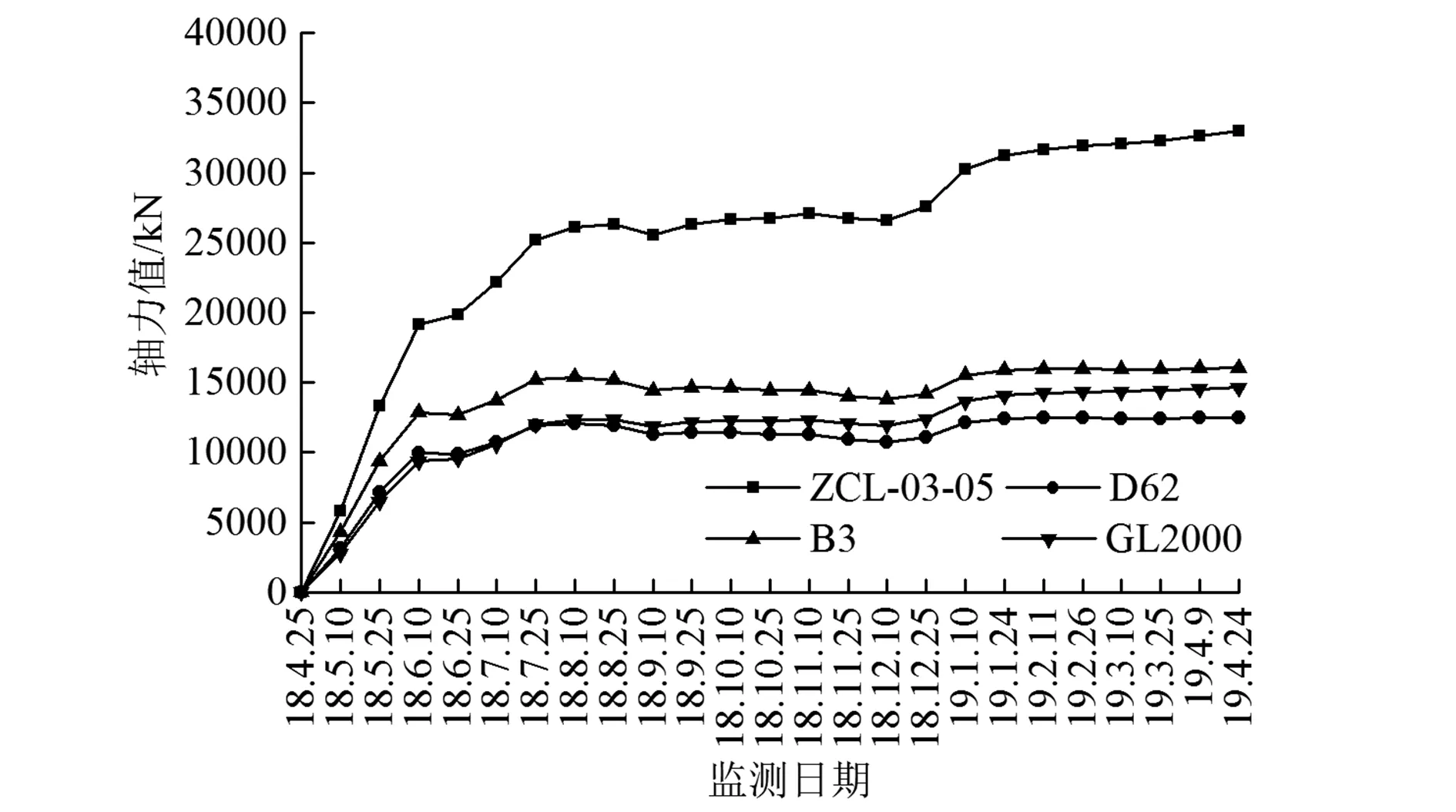
图5 ZCL-02-05监测点轴力实测值与理论修正值对比曲线

2.3 收缩徐变模型介绍

根据文献资料分析，在现有的混凝土收缩徐变模型中，计算精度较高、参数考虑较全面且领域内应用广泛的模型,主要有国内的D62模型(基于FIP90模型)、国外的B3和GL2000模型[10]：

(1)D62模型

徐变系数：φ0(t,t0)=φ0·βc(t-t0)

收缩应变：εcs(t,ts)=εCSO·βs(t-ts)

式中：t0为起始荷载施加龄期；ts为开始收缩龄期；t为计算截止龄期；φ0和βc(t-t0)均是与环境湿度、构件理论厚度、起始加载龄期和计算龄期等有关的参数；εCSO是与立方体平均抗压强度和环境湿度有关的参数；βs(t-ts)是与开始收缩龄期和计算龄期有关的参数。

(2)B3模型

徐变系数：

φ(t,t0)=E(t0)[q1+C0(t,t0)+Cd(t,t0,ts)]-1

收缩应变：

式中：E(t0)为加载龄期下的混凝土弹性模量；q1为单位应力下的瞬时应变；C0(t,t0)是与加载龄期和水灰比有关的参数；Cd(t,t0,ts)是与环境湿度、立方体抗压强度有关的参数；εs,∞是与立方体抗压强度和砼含水量有关的参数；τsh是与构件体表比和圆柱体抗压强度有关的参数。

(3)GL2000模型

徐变系数：

收缩应变：

εsp=εshuβRHβ(t0)

式中：φ(tc)为干缩修正系数；εshu是与水泥种类和圆柱体抗压强度有关的参数；βRH是与环境湿度有关的参数；β(t0)是与起始加载龄期和构件体表比有关的参数。

本文在上述模型基础上，考虑构件配筋对徐变系数的影响，引入徐变系数影响参数ks[4]：

式中：ne为钢筋与砼弹性模量比值；ρs为配筋率。

2.4 轴力修正值与实测值对比分析

利用上述3个理论模型对轴力实测值进行修正后，得到支撑轴力修正值。依据图3～图5给出了3个监测点轴力实测值与相应理论修正值的对比曲线。由图分析可知，D62、B3和GL2000模型均能明显地对实测值进行修正，各模型修正值在整个监测周期内变化曲线趋势相同，且数值较为接近。选取最后一次监测数据(监测时间2019年4月24日)分析可知，各模型对ZCL-01-05监测点实测轴力值(35115.0 kN)修正后的轴力分别为13 382.5 kN、17 195.2 kN和15 718.5 kN，以Ar表示理论模型对实测数据的修正幅度，则Ar分别为61.9%、51.0%和55.2%；对ZCL-02-05监测点实测轴力值(33 031.6 kN)修正后的轴力分别为12 504.4 kN、16 099.1 kN和14 678.0 kN，Ar分别为64.4%、54.2%和58.2%；对ZCL-03-05监测点实测轴力值(32 965.0 kN)修正后的轴力分别为12 476.3 kN、16 064.0 kN和14 644.7 kN，Ar分别为64.5%、54.3%和58.3%。

3 数值模拟结果及分析

3.1 计算模型介绍

为得到深基坑混凝土支撑较为真实的轴力值，采用数值模拟方法对整个基坑开挖过程进行模拟试验。图6分别给出了三维深基坑计算模型剖面图和基坑围护结构模型。如图6所示，整体计算模型尺寸长×宽×高=150m×120m×80m，将其划分为54 500个六面体单元，34 394个节点。模型中各项地层参数及基坑尺寸同本文1.1和1.2节内容。

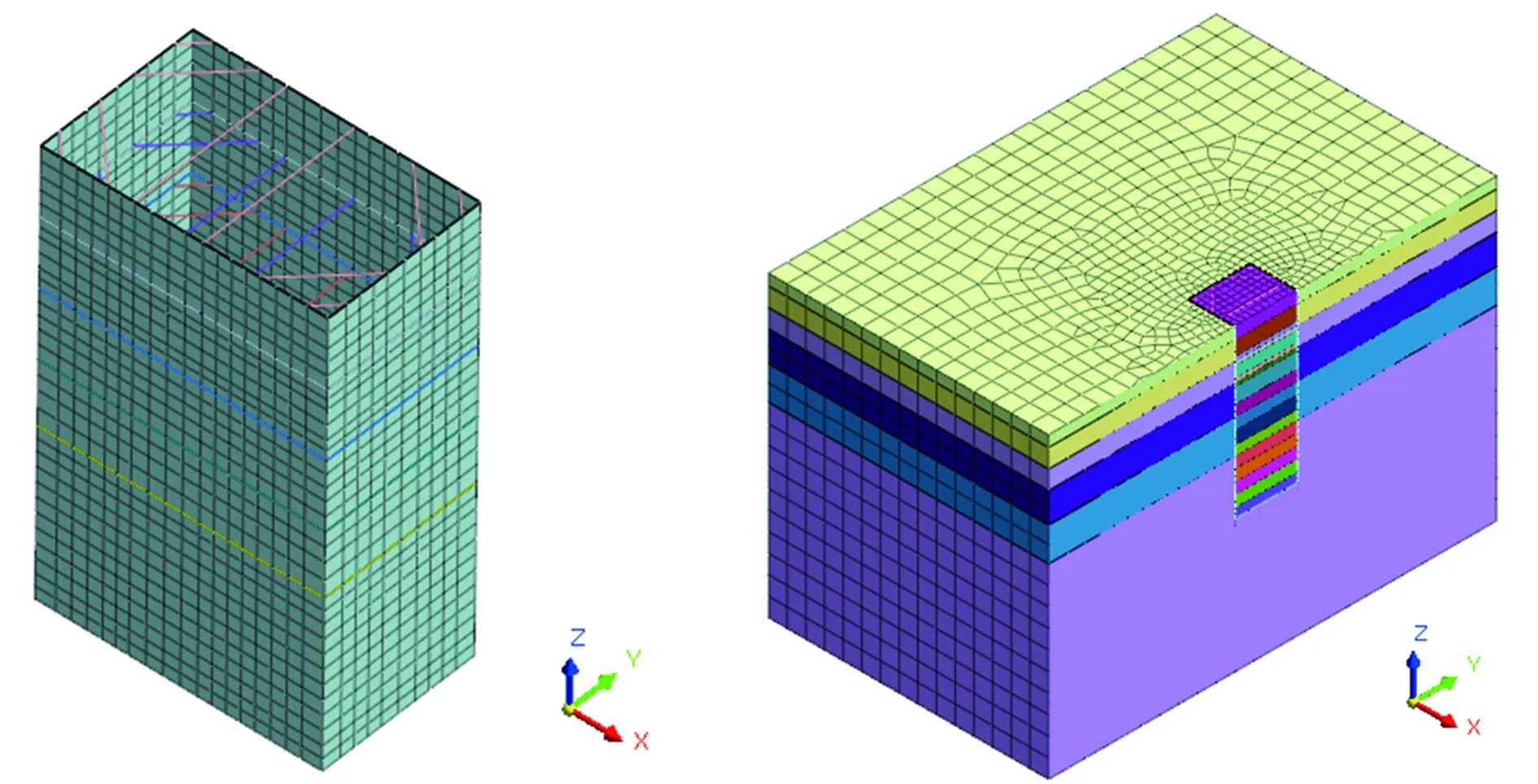
(a) 计算模型剖面 (b) 围护结构计算模型图6 深基坑数值计算模型

3.2 数值模拟结果分析

图7给出了基坑开挖至坑底后支撑轴力计算结果。由图7分析可知，在基坑深度方向，各道支撑平均轴力随深度增加而增大，第五道支撑平均轴力最大。第五道支撑中，轴力最大值出现在监测点ZCL-02-05所在的横撑，其值为15 231.1 kN；监测点ZCL-01-05和ZCL-03-05所在斜撑轴力值分别为14 985.6 kN、14 913.7 kN。

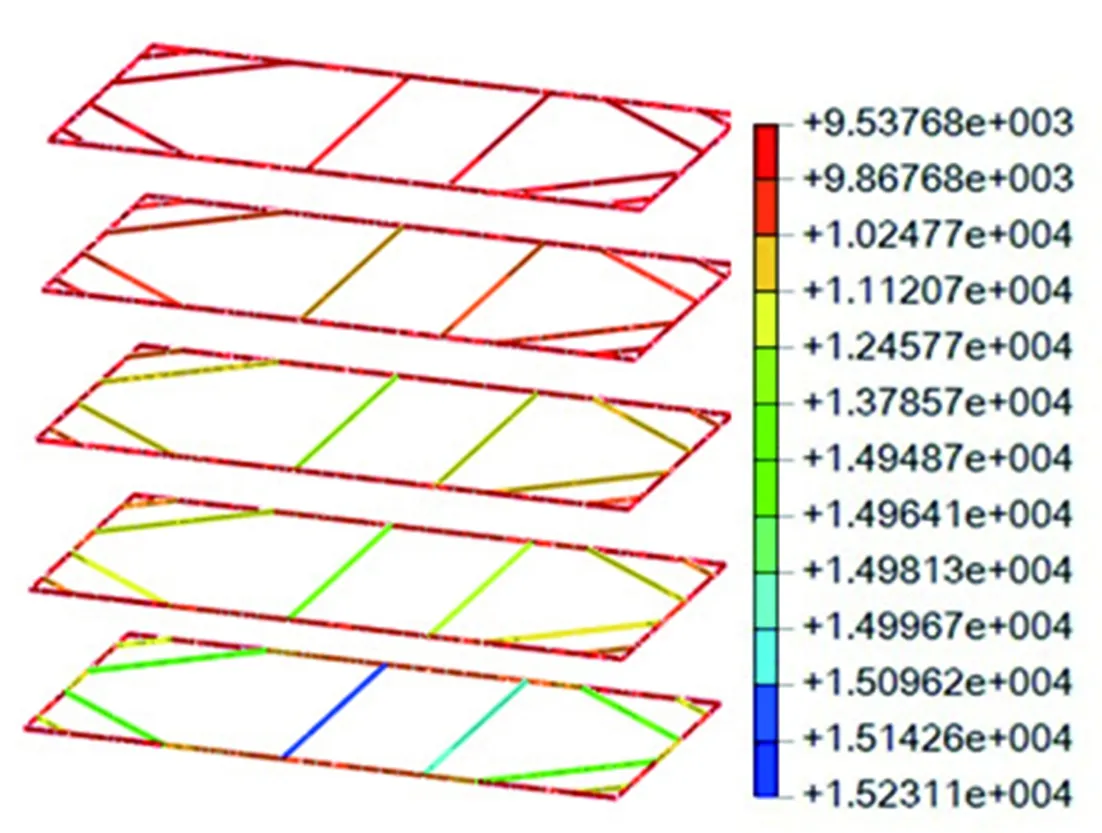
图7 支撑轴力计算结果

3.3 轴力修正值与模拟值对比分析

为进一步讨论各理论模型修正值的可靠程度，拟将其与相应的数值模拟结果进行对比。选取最后一次实测轴力值(监测时间2019年4月24日)对应的理论修正值与基坑开挖数值模拟得到的轴力计算值进行对比，如表2所示。由表2分析可知，各监测点轴力模拟值均介于相应理论修正值之间。以Dl表示轴力修正值与模拟值的偏离程度，对于ZCL-01-05监测点，Dl分别为10.7%、-14.7%和-4.9%；对于ZCL-02-05监测点，Dl分别为17.9%、-5.7%和3.6%；对于ZCL-03-05监测点，Dl分别为16.3%、-7.6%和1.8%。其中，Dl为正值表示理论修正值小于模拟值，负值表示理论修正值大于模拟值。

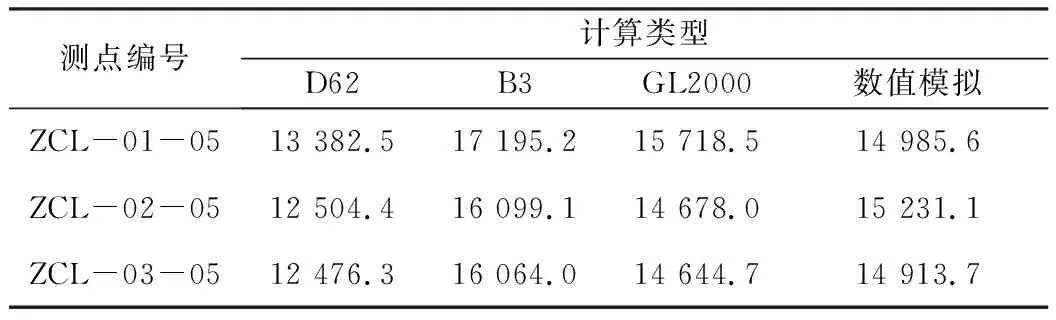
表2 轴力修正值与数值计算值对比 kN

4 收缩徐变模型对比分析

根据上述结果，各监测点理论模型对实测轴力值的修正幅度按大小顺序排列为：Ar(D62)>Ar(GL2000)>Ar(B3)模型；另一方面，各监测点轴力修正值与模拟值偏离程度绝对值按大小顺序排列为：对于ZCL-01-05监测点Dl(GL2000)

进一步对D62模型和GL2000模型在修正幅度上的表现进行分析，两模型在计算徐变系数时，分别选取了构件理论厚度和体表比作为计算参数，两个不同的结构特性参数直接导致徐变应变出现明显差异(相差约55个微应变)，进而引起轴力修正值相差约2000 kN。通过将GL2000模型中的体表比换算为构件理论厚度后，其相应的轴力修正幅度明显提升。

5 结论

(1)混凝土收缩徐变是造成支撑轴力实测值超限的主要原因，由收缩徐变产生的轴力值最高可达实测值的64.5%。

(2)在D62、B3和GL2000常用的3个收缩徐变模型中，GL2000模型整体表现最为优异，计算结果更符合工程实际。

(3)在GL2000模型计算混凝土徐变系数过程，若将计算参数中的体表比换算为构件理论厚度，可明显增加模型的修正幅度，进一步提升模型整体性能。