地震作用下水-轴对称柱体相互作用的子结构分析方法
2021-03-02王晓静王丕光杜修力程星磊
王晓静,赵 密,王丕光,杜修力,程星磊
(北京工业大学城市与工程安全减灾教育部重点实验室,北京100124)
随着经济的发展,近海工程结构的发展也越来越受到关注,如海上风电、人工岛、跨海桥梁等[1-3]。地震作用下水-结构的相互作用会在结构的表面产生动水压力作用,该动水压力会影响结构的动力响应和动力特性[4-6]。因此研究水-柱体结构相互作用对近海工程结构的抗震设计具有重要的意义。
地震作用下水-结构的相互作用的研究可以追溯到1933年Westergaard 对竖直坝面上的地震动水压力的求解。地震作用下水-柱体相互作用的研究则始于1965年椭圆截面刚性柱体上动水压力的推导[7]。之后,Chopra 在讨论了水体压缩性和表面波对圆柱结构地震响应的影响[8]。水-柱体结构相互作用的分析方法主要有解析法、数值法、和物理实验法[9]等。解析法是通过首先求解水-柱体结构相互作用的定解问题的动水压力解析式,进而将动水压力公式代入结构的运动方程对结构进行动力响应分析[10-15]。解析法一般只能分析几何形状简单的等截面柱体结构,如圆柱[10-13]和椭圆柱[14-15]。数值法则是基于有限元[16-17]、边界元[18-19]、无限单元[20]等数值方法分析水-柱体结构相互作用问题的方法,数值方法对结构的几何形状没有那么高的要求,可以求解几何形状复杂的结构或者倾斜结构。
轴对称柱体结构是近海工程中常见的结构形式,如圆锥柱体、复合桶形基础等[17,21-22]。数值方法可以用于求解地震作用下水-轴对称柱体的相互作用问题。近海工程中一般将水体介质视为无限域,数值模型中可通过引入人工边界条件将水体分为近场有限域和远场无限域。近场有限域可以用动力有限元法进行模拟,远场无限域则用人工边界条件模拟[23-26]。王丕光等[24]提出了一种三维圆柱形高精度时域人工边界条件求解三维复杂结构与水体的动力相互作用问题。本文则是针对地震作用下水-轴对称柱体的相互作用问题的特点,采用分离变量法将三维问题转变为一种环向解析、竖向和径向数值的二维分析模型;二维分析模型中,基于比例边界有限元法(SBFEM)[27-29]推导了一种模拟远场无限域的高精度人工边界。比例边界有限元法能够降低问题的维度,从而减小计算量、提高计算效率,并且能自动满足无限远处的辐射边界条件。
1 问题描述
地震作用下水-轴对称柱体的动力相互作用问题如图1 所示,图中h表示水深,H为柱体高度;在直角坐标系和柱坐标系中,z轴为沿着柱体轴线向上,坐标原点位于柱体底部;a(z)表示z处截面半径。假定地基为刚性,地面运动沿x方向运动,相应的位移时程为ug;结构-水体系统初始静止;水体假定为小扰动不可压缩流体,并忽略表面重力波的影响,水体的密度为 ρw=1000 kg/m3。柱坐标系(r,θ,z)下水体的控制方程为:
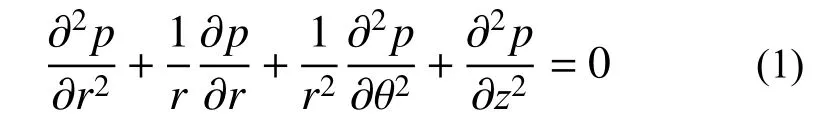
式中,p表示水体的动水压力。

图1 轴对称结构-水相互作用示意图Fig.1 Axisymmetric cylinder-water interaction
水底、水面和水与结构交界面的边界条件以及无穷远处的辐射条件分别为:

动力压力p的可以通过分离变量的方式并结合边界条件表示为p=p1(r,z,t)cosθ,则相应的轴对称结构-水相互作用问题的控制方程和边界条件可以用动水压力的环向分量p1表示为:
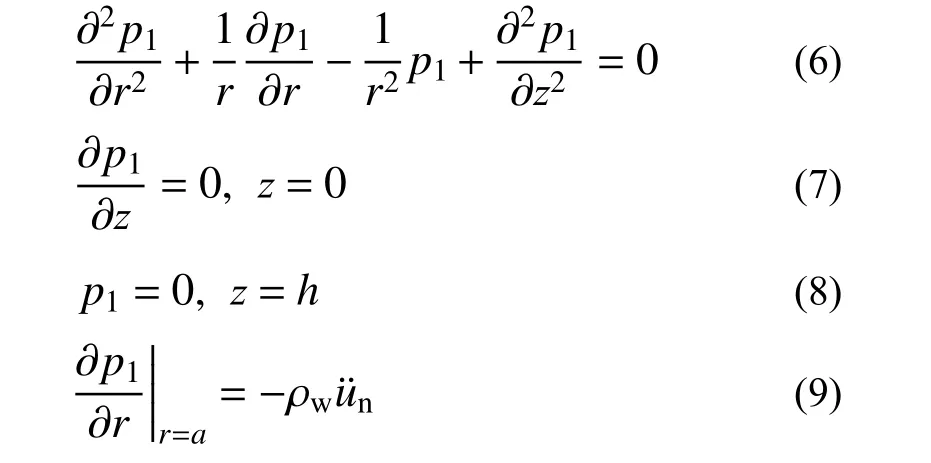
为方便叙述在下文的推导过程中p1称为动水压力。
在r=R0处引入人工边界条件,则无限域水体可以分为近场有限域 ΩI和远场无限域 ΩII。近场有限域可以用轴对称有限元离散。
2 轴对称有限元推导

采用与有限元相同的四节点四边形单元等参单元变换,再利用高斯积分即可得到刚度矩阵的值。
3 高精度人工边界条件
3.1 比例边界坐标变换
基于比例边界中心线的思想,本文将oz轴选取为比例边界中心线,如图2所示,图中比例边界坐标 ξ 和 η,为局部坐标。径向坐标 ξ可以看作是比例系数,因此域内任一点的坐标(r,z)可以用局部比例边界坐标 ξ 和 η表示为:

式中:N=N(η)=[(1-η)/2 (1+η)/2]为形函数;zb=[z1z2]T为边上的节点坐标。

图2 SBFE 坐标变换Fig.2 Thetransformation of SBFE coordinates

3.2 比例边界有限元方程
对控制方程式(6)运用加权余量法可得:

将相应的坐标变换关系式(21)、式(22)和式(23)代入式(24),并对其中的两项进行分部积分得:
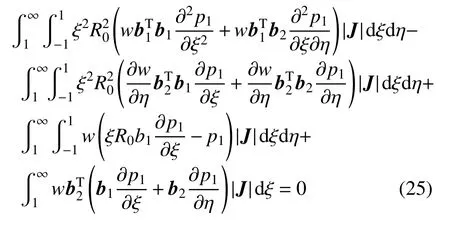
对动水压力和权函数采用相同的形函数插值:

式中:p1=p1(ξ)为单元节点动水压力向量;w=w(ξ)为权函数向量。定义B1=b1N,B2=b2N,η,下标撇号表示导数,如N,η即表示形函数N 对坐标η的导数。
将式(26)、式(27)代入式(25),并消去任意权函数w和对 ξ的积分可得:
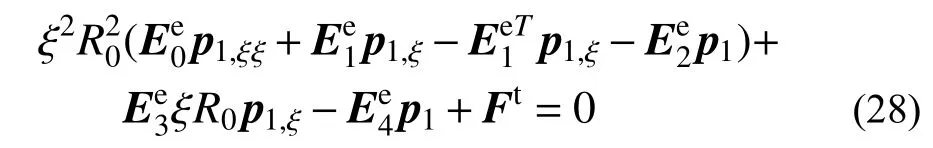
其中:

将式(28)沿人工边界处进行装配,消去系数为零的项,并利用上下表面的边界条件可得:

4 水-轴对称柱体系统的时域方程
4.1 水体有限元方程

整个水域的动水压力可以表示为:

4.2 水-轴对称柱体系统的时域方程
柱体结构可以用梁单元进行模拟,单元刚度和质量矩阵可以用一下公式表示[30]:

5 数值算例
本文中算例的结构的弹性模量、密度、泊松比和阻尼比分别为:21 GPa,7800 kg/m3,0.3和0.02,结构的厚度为0.06 m。图3为本文中选取的作用在刚性地基上的地震动时程曲线,图4为对应的地震动的傅里叶幅值曲线。
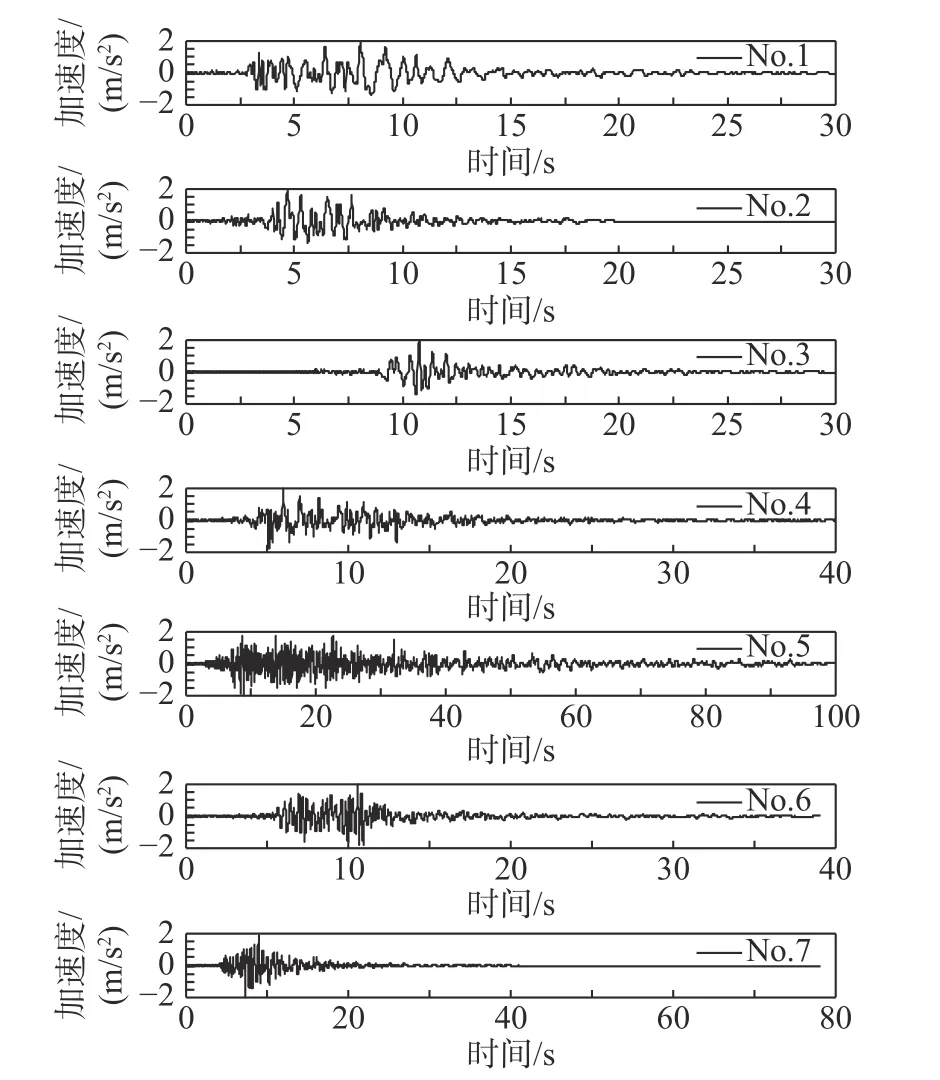
图3 地震动时程Fig.3 Time history of earthquakes
5.1 方法验证
首先,对轴对称结构的等效梁单元进行验证。表1为本文轴对称结构的等效梁单元和ABAQUS中的实体梁单元计算的自振频率的比较,可以看出相对误差在5%以内,因此本文选用的等效变换方法是符合精度要求的。
其次,对二维分析模型中的人工边界的验证。分别选取等截面圆柱和圆锥柱体两个模型:模型1等截面圆柱的半径和高度分别为3 m、80 m,模型2圆锥形柱体的半径、倾角和高度分别为a=3 m 、θ0=atan(80/1)和80 m。模型1的参考解为解析解,模型2的参考解为20 000×80的扩展有限元解,网格大小为5×5。人工边界的设置在r=50m 处。图5为刚性轴对称柱体上的动水力分布本文解和参考解的对比。由图5可以看出,采用本文提出的人工边界条件得到的本文解与参考解极好地吻合。
最后,对本文提出的水-轴对称相互作用的子结构分析方法的验证。等截面圆柱的参考解为将柱体结构与动水压力的解析解耦合求得的结构动力反应;圆锥柱体模型的参考解为柱体结构有限元方程与动水力的扩展有限元方程与柱体结构有限元方程耦合解得的结构动力反应。在模型1、模型2施加图3所示的编号为No.1地震动荷载,将结构的顶部位移作为参考量。图6为结构顶部位移响应本文解和参考解的对比。由图6可以看出本文方解与参考解吻合较好。
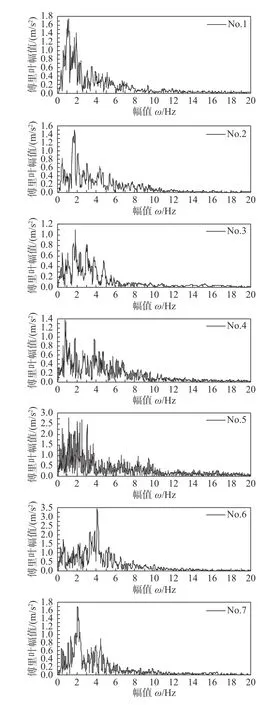
图4 地震动的傅里叶幅值曲线Fig.4 Furrier amplitude spectrum of ground motions

表1 等效变换梁单元和实体单元的自振频率Table 1 The natural frequency of vibration comparison of solid element and equivalent beam
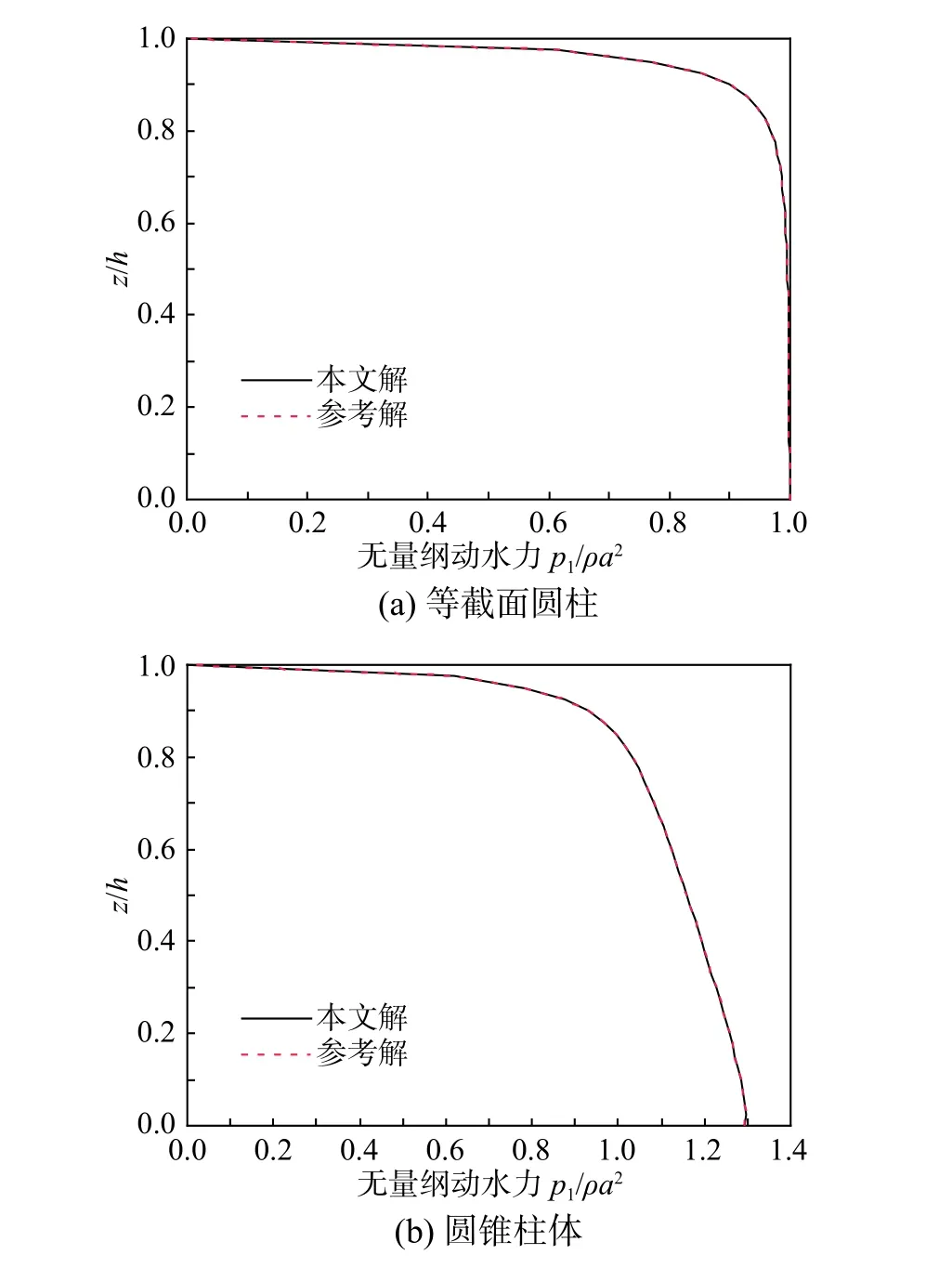
图5 刚性柱体上无量纲动水力沿高度分布Fig.5 The distribution of dimensionless hydrodynamic pressure
5.2 应用分析
计算了不同水深时水-轴对称结构相互作用系统的地震响应,分析水深对水-轴对称结构相互作用。引入无量纲系数Ru=uim/u0m,其中uim表示不同水深时水-轴对称结构相互作用时位移响应的最大值,u0m表示轴对称结构在空气中时位移响应的最大值。
以模型2为例,分别计算了水深为20 m、40 m、60 m 和80 m 时,荷载分别为图3所示的7条地震动时的结构的动力响应;图7为Ru随水深的变化。由图7可以看出,地震动水压力对结构地震反应的影响随水深相对结构高度(h/H)的增加呈增大趋势,这主要是由于作用在结构上的地震动水压力随水深的增加而增大。需要指出的是,由于不同地震动的频谱特性不同,因此不同地震动作用下动水压力对结构地震响应的影响也不相同。
定义自振频率降低率为:

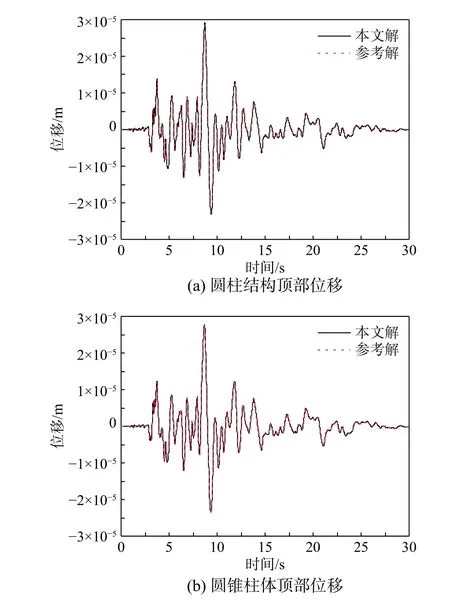
图6 柱体顶部位移响应Fig.6 Top displacement of the axisymmetric structure
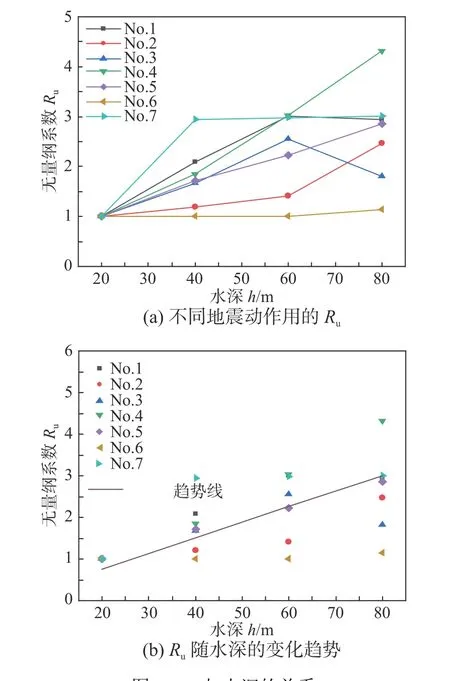
图7 R u 与水深的关系Fig.7 R u vary with different earthquakes
式中,ωws和ωs分别是指水-结构相互作用系统的自振频率和结构无水时的自振频率。
表2为不同水深时水-轴对称相互作用系统的自振频率。表3为不同水深时自振频率的相对值。由表2和3可以看出当水深相对结构高度较小时(h/H≤0.25),系统的基频和结构无水时的基频相差不大,由图7也可以看出此时结构的地震响应与无水时没有明显差异;这表明水深相对结构高度较浅时,地震动水压力对柱体结构地震响应的影响可忽略。随着水深相对结构的高度的增大(0.25<h/H≤1),系统的频率降低率逐渐减小,自振频率的减低可能会使得系统的二阶自振频率出现在地震动的卓越频率范围内,图7中也可以看出此时结构的地震响应与无水时相差较大;因此水深相对结构高度较深时,地震动水力对柱体结构的动力响应和自振特性的影响不可忽略。

表2 水-轴对称结构相互作用系统的自振频率Table2 Thenatural frequency of vibration of wateraxisymmetric interaction system
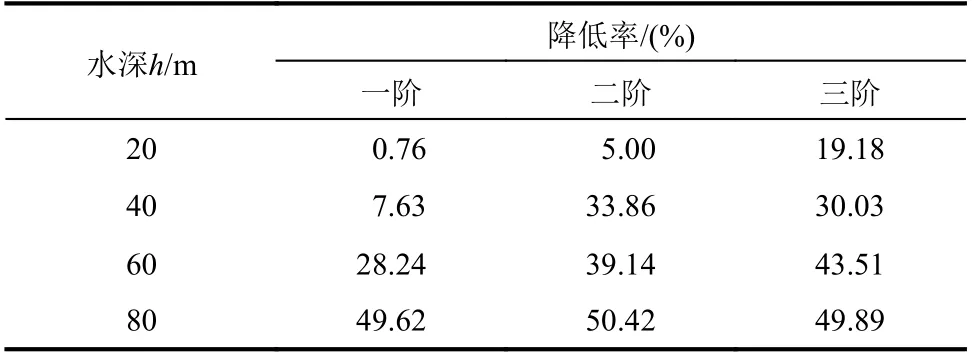
表 3自振频率降低率Table 3 The reduction ratio of natural vibration frequency
6 结论
基于不可压缩水体,本文提出了一种地震作用下水-轴对称柱体相互作用的动力响应的子结构分析方法。首先将水体三维模型转化为环向解析、竖向和径向离散的二维模型,其次用高精度人工边界条件模拟无限域水体的作用,在保证了精度的同时大大提高了计算效率。
数值算例中分别验证了结构的等效梁单元、动水压力和水-结构动力相互作用耦合模型的精确性。以圆锥柱体为例分析了地震作用下水深对水-轴对称结构相互作用的地震响应的影响,数值算例表明随着水深的增加,动水力对结构的自振频率和动力响应的影响呈增大的趋势。
由于本文提出的子结构可以将水-轴对称结构的相互作用通过附加质量的模拟,易于在商业有限元软件中实现和方便于工程应用。
