考虑荷载分布的多跨连续钢-再生混凝土组合板长期性能研究
2021-03-02王庆贺梁永泽张逸超任庆新
王庆贺,梁永泽,张 欢,张逸超,任庆新
(1.沈阳建筑大学土木工程学院,沈阳110168;2.哈尔滨工业大学结构工程灾变与控制教育部重点实验室,哈尔滨150090)
近年来,钢-混凝土组合结构以其施工速度快、施工质量高等特点得到了工程界的广泛关注[1];且其具有承载力高、抗震性能好等优势,可显著降低构件截面尺寸,这也间接提高了工程结构的经济效益[2-5]。钢-混凝土组合结构中可采用压型钢板-混凝土组合楼板,压型钢板在施工过程中兼做施工模板,在使用过程中充当受拉构件,典型的施工过程见图1。由于工程结构中楼板对混凝土抗压强度的要求较低(一般低于C40),而且受底部压型钢板的密闭影响,组合板构件无需验算其正弯矩区的裂缝宽度[6]。基于此,部分学者对压型钢板-再生混凝土组合板的短期静力性能(抗弯性能与纵向剪切性能)进行试验初探[7-12],尝试采用废弃混凝土骨料替代天然砂石,以期促进废弃混凝土的资源化应用。初步结果表明,虽然再生混凝土各项力学性能较普通混凝土差,例如,采用100%再生粗骨料取代率时,弹性模量降低20%~40%[13],但钢-再生混凝土组合板的短期静力性能与钢-普通混凝土组合板相近[7-12]。

图1 压型钢板-混凝土组合楼板施工过程Fig.1 Typical construction process of profiled steel-concrete composite slabs
阻碍钢-再生混凝土组合板工程应用的一个关键因素为其长期性能,这主要体现在:1)与普通混凝土相比,再生混凝土长期变形显著增大,取代率为100%时,收缩变形增大40%~100%、徐变变形增大30%~110%[14],而且由于压型钢板的密闭效应,组合板中再生混凝土相对湿度(收缩变形和徐变系数)沿截面高度是非均匀分布的,进而组合板中将产生附加挠曲[1,3];2)实际工程中一般采用多跨连续组合板形式(见图1),且需承受多种均布及非均布荷载作用,但现有研究大都针对单跨组合板展开[15-22],可提供的参考资料较少。
前期研究中,Gilbert 等[16]指出钢-普通混凝土组合楼板中混凝土发生非均匀收缩时会导致组合板的开裂和翘曲变形。Gi1bert 等[16]、Abas等[17]和Bradford[18]通过测量组合板沿截面高度方向的非均匀收缩分布,量化了非均匀收缩对钢-混凝土组合板长期挠度的影响,并给出了几种常用组合板收缩模型;Al-deen 和Ranzi[19]通过试验研究了组合板收缩梯度变化规律,提出了非均匀收缩的理论公式。课题组前期对钢-再生混凝土单跨组合板开展了系列研究,提出了钢-再生混凝土组合板的非均匀收缩模型[23],并基于国内外试验研究,建立了考虑非均匀收缩、徐变和混凝土开裂综合影响的单跨钢-再生混凝土组合板非线性数值模型,提出了长期挠度计算公式[24]。
对于多跨连续组合板,国内部分学者对其抗弯和抗剪性能进行了系列研究[25-26];近年来,Gholamhoseini等[27]和Zhang 等[28]对两跨连续组合板的长期性能进行了试验初探,发现混凝土长期收缩应变对组合板的挠度影响显著。
由于现有研究多针对单跨钢-普通(再生)混凝土组合板展开,本文拟基于ABAQUS软件,建立多跨连续钢-再生混凝土组合板有限元模型,模型中采用温度场模拟混凝土的非均匀收缩变形,基于龄期调整的有效模量法模拟混凝土的非均匀徐变特性,利用已有试验研究成果验证本文模型的可靠性;在此基础上,量化均布及非均布荷载作用时,再生粗骨料掺入对多跨连续组合板长期性能的影响,为其工程应用提供参考性建议。
1 有限元模型建立
由于现有理论公式不能有效考虑混凝土沿跨度方向不均匀开裂的影响[16],采用MATLAB编写的模型未能考虑混凝土受拉刚化的贡献[1-3],本文采用ABAQUS软件建立组合板长期性能有限元模型,如图2所示,模型主要包括压型钢板、混凝土、钢筋和支座垫板四部分。
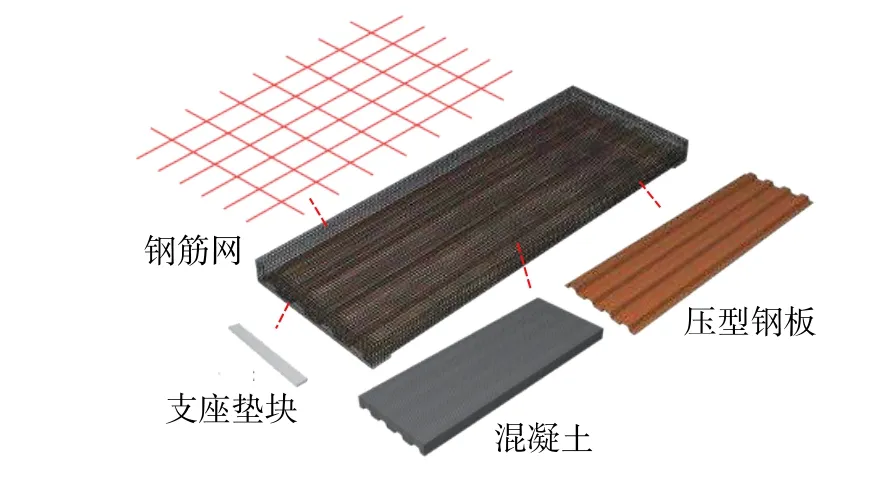
图2 组合板有限元模型Fig.2 FEA model of composite slabs
1.1 材料力学模型
1.1.1钢材
现有组合板长期试验中,压型钢板及钢筋均未发生断裂破坏,因此,模型中不考虑钢材的断裂,弹性模量及泊松比分别为206 GPa 和0.3。
支座处采用刚性垫块,弹性模量设为钢材的10倍。压型钢板一般采用冷加工,应变硬化和伸长率较低,屈服强度与极限强度相近,因此采用理想弹塑性模型。受力及分布钢筋采用的应力-应变模型见图3,OA段为弹性阶段,钢筋在A点达到屈服强度fy,OA段的斜率为弹性模量Es;BC段为钢筋的强化阶段,钢筋在B点开始进入强化阶段,B点对应的应变为εp,强化初始弹性模量为Ep,在C点达到极限强度fu,对应的应变为εu。
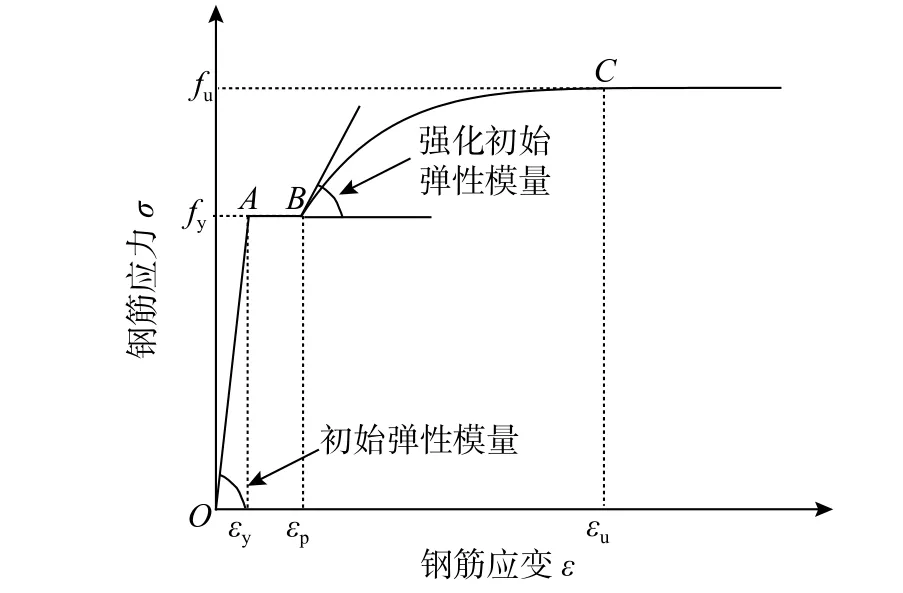
图3 钢筋应力-应变曲线Fig.3 Stress-strain curve of reinforcement
1.1.2混凝土
有限元模型的混凝土采用塑性损伤模型,相关塑性参数参考文献[29]选取。混凝土的应力-应变本构关系见图4,再生混凝土受压性能随再生粗骨料取代率r的增大而降低,参照文献[7]所述公式进行计算:
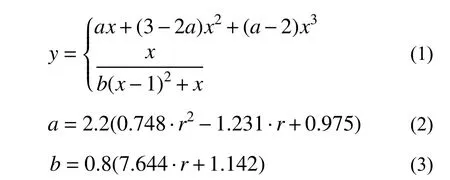
式中:x为压应变εc与峰值压应变εc0之比;y为压应力σc与峰值压应力fc之比;a与b为再生粗骨料取代率的影响系数。
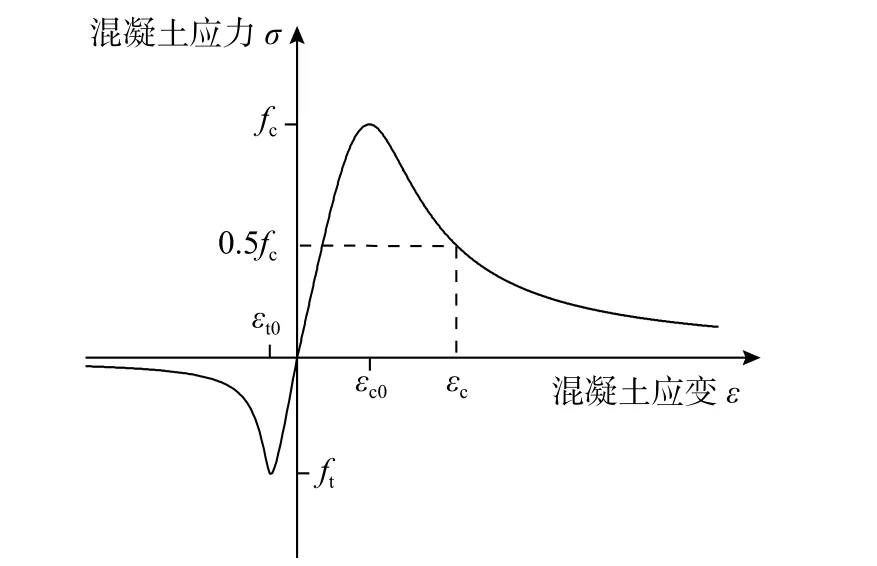
图4 混凝土单轴应力-应变曲线Fig.4 Uniaxial stress-strain curveof concrete
再生混凝土受拉性能参照文献[7]中公式计算:

式中:x为拉应变εt与峰值拉应变εt0之比;y为拉应力σt与峰值拉应力ft之比;c为参考点处的正切模量与余切模量之比,c=1.19+0.07r。
再生混凝土与普通混凝土抗压强度相同的前提下,再生混凝土抗拉强度ft,RAC以及峰值拉应变εt0,RAC参照文献[7]计算:

普通混凝土弹性模量Ec,NAC参考欧洲EC2规范进行计算[30];对于采用残余砂浆含量已知的再生粗骨料时,再生混凝土弹性模量参考笔者提出的公式计算[23],对于采用残余砂浆含量未知的再生粗骨料时,再生混凝土弹性模量参考再生混凝土结构技术规程的建议[31]。
混凝土的长期变形主要包括收缩变形及徐变变形。混凝土收缩变形εsh(t,z)受混凝土孔隙率、相对湿度等因素影响,主要分为干燥收缩εsh,dry与自生收缩εsh,au。考虑到钢-混凝土组合板中沿厚度方向的相对湿度分布是非均匀的,因此,混凝土的收缩变形也是非均匀分布的[23]。虽然部分文献提出了非线性收缩分布形式,但考虑其应用较为复杂,本文仍采用线性收缩模型(见图5(a))[23],组合板顶部及底部的收缩变形见式(7)和式(8):
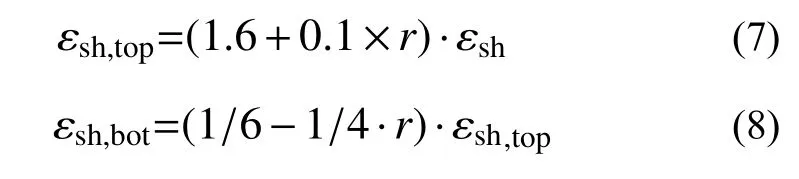
式中:εsh,top与εsh,bot分别为组合板顶部与底部混凝土的收缩;εsh为混凝土总收缩,εsh=εsh,dry+εsh,au。

与非均匀收缩分布相似,组合板中混凝土徐变系数沿截面高度亦呈现非均匀分布形式,见图5(b)。混凝土的徐变变形εcr(t,t0,z)主要与徐变系数φ(t,t0,Z)有关,徐变系数φ(t,t0,z)由名义徐变系数φ0和徐变发展系数βc(t,t0)确定。本文基于EC2规范[30]及前期研究结果[32]得到单面密闭的再生混凝土徐变系数,认为组合板顶面相对湿度与环境相对湿度相同,底部相对湿度采用90%[23]。再生混凝土的徐变系数计算考虑残余砂浆系数(KRCA)、基体混凝土强度系数(kw/c)与可恢复徐变系数(KRC)的综合影响,具体公式参见文献[32]。
1.2 单元选取与网格划分
有限元模型中,压型钢板采用S4R 壳单元,钢筋采用T3D2桁架单元,支座垫板采用八节点线性六面体实体单元(C3D8R);采用热传导单元DC3D8模拟传热阶段的混凝土,采用实体单元C3D8R 模拟静力分析阶段的混凝土。
网格划分时,按照组合板尺寸,确定基本网格尺寸为25 mm ~ 30 mm,由于肋处混凝土形状不规则,肋部混凝土网格尺寸采用10 mm ~ 25 mm[29]。压型钢板、钢筋和垫板等构件的网格尺寸与混凝土网格对应。
1.3 分析过程
有限元分析包括混凝土温度场建立及组合板静力分析阶段。模型中采用强迫混凝土降温措施模拟混凝土的非均匀收缩变形,并采用基于龄期调整的有效模量法模拟混凝土非均匀徐变特性。需要指出,通过采用混凝土收缩和徐变性能预测模型,本文有限元分析可以考虑组合板尺寸、环境湿度、抗压强度、持荷时间等因素的影响。
温度场建立阶段:此步骤所建温度场用于后续混凝土长期收缩变形的模拟,本阶段采用Heat transfer 分析,绝对零度为-273℃,整体初始温度为T0,Stefan-Boltzmann 常数为5.67×10-8,导热系数为1.355 W/(m·K),比热容为1230.5 J/(kg·K)。
静力计算阶段主要包括3 个步骤:1)混凝土温度场施加,此步骤用于模拟组合板在瞬时加载前,混凝土仅受收缩作用下的结构响应;2)荷载施加,此步骤模拟组合板在外荷载(自重及活荷载)作用下的结构瞬时响应,该步骤延续至全部加载步结束;3)混凝土温度场再次施加,该步骤用于模拟组合板在外荷载、非均匀收缩、非均匀徐变共同作用下的长期性能响应。
2 有限元模型验证
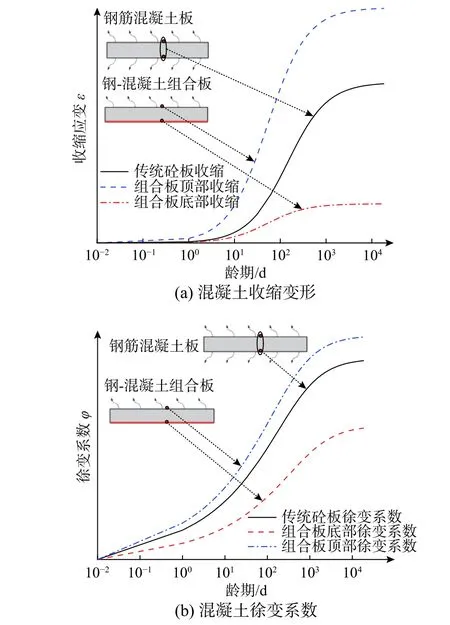
图5 混凝土长期性能曲线Fig.5 Time-dependent behavior curve of concrete
利用收集到的18组钢-混凝土组合板足尺试验数据验证本文模型的可靠性,试件包括单跨组合板和两跨连续组合板。单跨组合板采用的再生粗骨料取代率包括0%、50%和100%,压型钢板包括开口型、闭口型以及钢筋桁架楼承板;两跨连续组合板采用普通混凝土和开口型压型钢板。组合板跨度l采用3000 mm ~3300 mm,厚度d采用120 mm~180 mm,混凝土抗压强度fc为26.6 MPa ~43.6 MPa,环境相对湿度RH采用42.8%~70.0%,持荷时间为t为105 d~ 348 d,分布钢筋配筋率0%~0.6%,荷载Q为0 kPa~17.6 kPa,表1给出了现有试验的参数和关键试验结果。
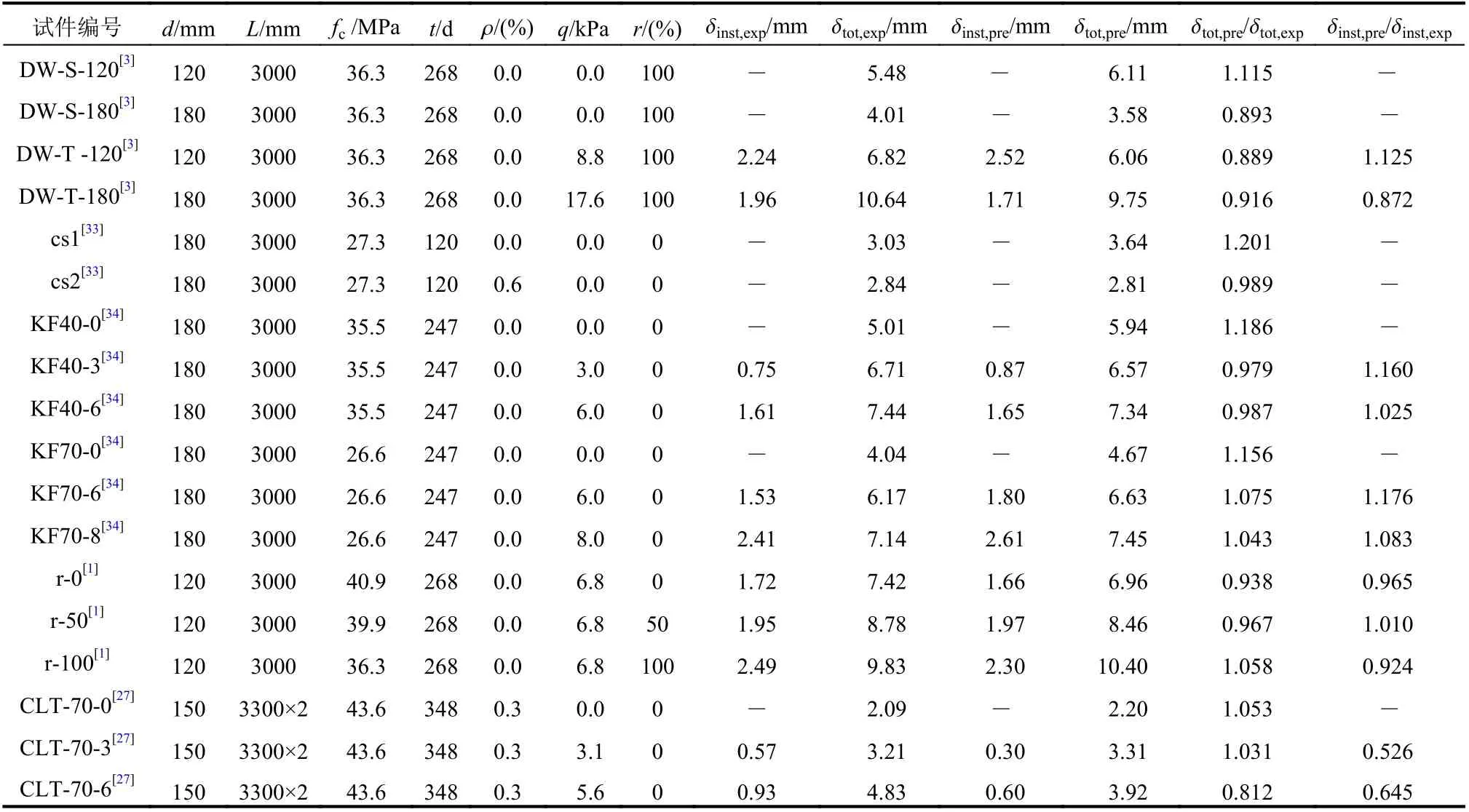
表1 现有组合板长期性能试验参数与主要结果Table 1 Long-term test parameters and results of composite slabs
2.1 单跨钢-混凝土组合板长期性能预测结果
2.1.1采用不同厚度的板件预测结果
图6对比了不同厚度的钢-再生混凝土组合板分别在收缩作用下(图6(a))及收缩、徐变与外荷载共同作用下(图6(b))的长期挠度试验与预测结果,试件均采用100%取代率,跨度l均为3000 mm,厚度d分别为120 mm 和180 mm。仅在收缩作用下,厚度为120 mm 和180 mm 的试件268 d 跨中挠度实测值分别为5.48 mm 和4.01 mm,采用模型得到的预测值分别为6.11 mm 和3.58 mm,试验值与预测值分别相差11.5%和10.7%,本文模型可以有效预测非均匀收缩产生的附加挠度。
试件28 d 承担8.8 kPa(d=120 mm)和17.6 kPa(d=180 mm)外荷载时,两个试件的瞬时挠度分别为2.24 mm 和1.96 mm,预测值分别为2.52 mm和1.71 mm,预测值与试验值最大相差12.7%;组合板268 d 跨中挠度实测值分别为10.64 mm 和6.82 mm,预测值分别为9.75 mm 和6.06 mm,预测值与试验值最大相差11.1%。本文模型可有效预测钢-再生混凝土组合板在外荷载、收缩和徐变共同作用下的长期挠度。
2.1.2采用不同分布钢筋配筋率的板件预测结果
图7对比了采用不同配筋率的钢-混凝土组合板长期挠度试验与预测结果,试件跨度l和厚度d分别为3000 mm 和180 mm。两个试件受压区分布钢筋的配筋率分别为0%(cs1试件不配分布钢筋)和0.6%(cs2试件配置5 16分布钢筋)。可以发现,有限元结果与试验结果吻合较好,60 d 时,无配筋及配筋的组合板挠度实测结果分别为2.28 mm和2.07 mm,预测结果分别为2.21 mm 和1.81 mm,两者分别相差3.0%和12.6%;120 d 时,无配筋及配筋组合板跨中挠度分别为3.03 mm 和2.84 mm,预测结果分别为3.64 mm 和2.81 mm,两者分别相差20.3%和1.2%。值得一提的是,试验结果表明配置受压区分布钢筋对组合板长期挠度的影响较小,120 d 时两个试件的跨中挠度仅相差6.4%,这与有限元结果存在一定的差异,两个试件的有限元预测挠度相差22.8%。作者认为,该试验的测量时间仅为120 d,试件挠度还在显著增长,后续应进行更长时间的试验研究,分析受压区钢筋配筋率对组合板长期挠度的影响。
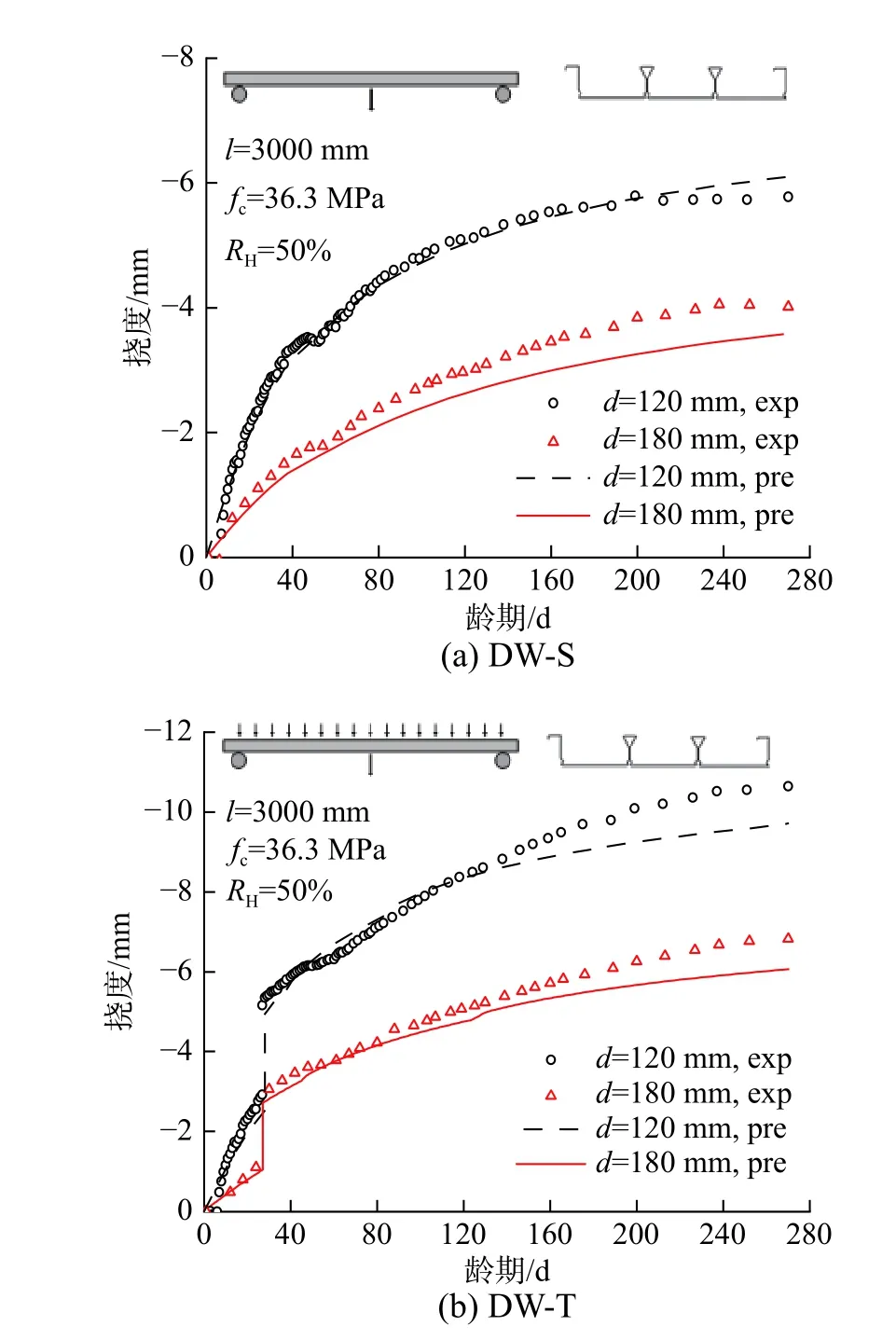
图6 不同厚度的组合板挠度试验与有限元结果对比[3]Fig.6 Comparison between measured and numerical timedependent deflection of composite slabs with different thicknesses[3]

图7 不同分布钢筋配筋率的组合板挠度试验与有限元结果对比[33]Fig.7 Comparison between measured and numerical timedependent deflectionsof composite slabswith different reinforcement ratios[33]
2.1.3采用不同荷载等级的板件预测结果
图8比较了钢-普通混凝土组合板在不同荷载作用下的长期挠度试验结果与预测结果,组合板采用开口型KF40(图8(a))与KF70(图8(b))压型钢板,试件跨度l为3000 mm,厚度d为180 mm,外荷载为0 kPa~8.0 kPa。钢-混凝土组合板跨中挠度随着外荷载的增大逐渐增加,其中KF40-3和KF40-6试件在承受3.0 kPa 和6.0 kPa 外荷载的瞬时挠度分别为0.75 mm 和1.61 mm,预测值为0.87 mm 和1.65 mm,预测结果与试验结果分别相差15.7%和1.9%;KF70-6和KF70-8试件承受6.0 kPa和8.0 kPa 外荷载的瞬时挠度分别为1.53 mm 和2.41 mm,预测挠度分别为1.80 mm 和2.61 mm,预测结果与试验结果分别相差19.7%和8.3%。
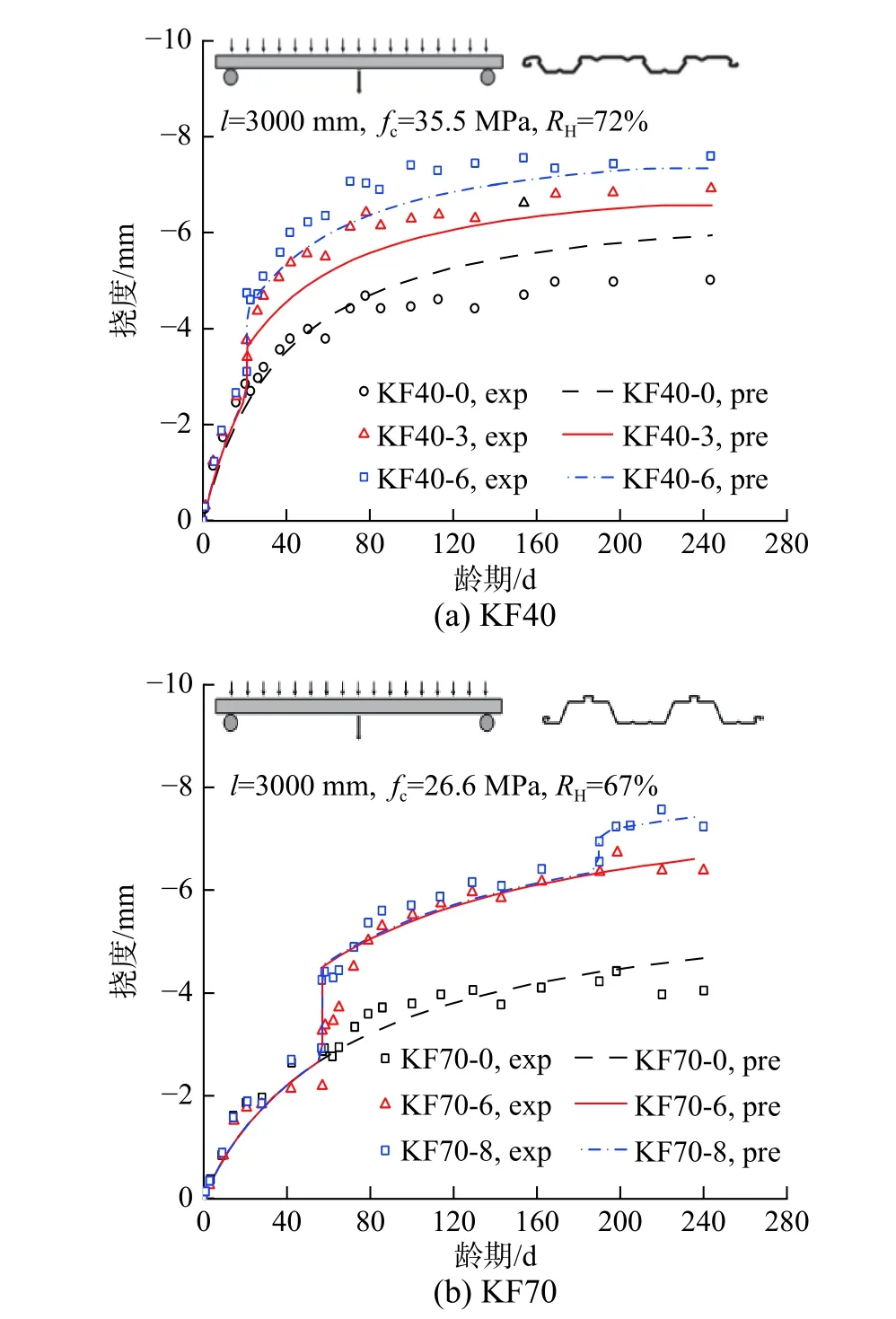
图8 不同荷载等级的单跨组合板挠度试验与有限元结果对比[34]Fig.8 Comparison between measured and numerical timedependent deflections of single-span composite slabs with different loading levels[34]
服役龄期为247 d 时,试件KF40-0、KF40-3和KF40-6的跨中挠度分别为5.01 mm、6.71 mm和7.44 mm,预测结果分别为5.94 mm、6.57 mm 和7.34 mm,预测结果与试验结果分别相差18.6%、2.1%和1.3%;试件KF70-0、KF70-6和KF70-8在247 d 的跨中挠度分别为4.04 mm、6.17 mm 和7.14 mm,预测结果分别为4.67 mm、6.63 mm 和7.45 mm,预测结果与试验结果分别相差15.7%、7.5%和4.3%。由对比结果可知,本文模型可有效预测不同荷载等级下的非均匀收缩、徐变和外荷载产生的长期挠度。
2.1.4采用不同取代率的板件预测结果
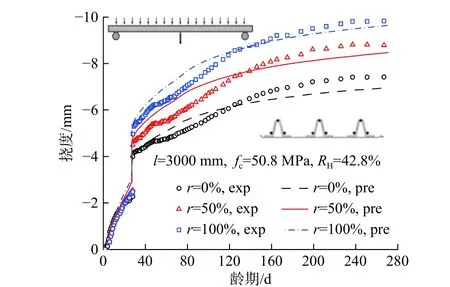
图9 不同取代率的组合板挠度试验与有限元结果对比[1]Fig.9 Comparison between measured and numerical timedependent deflections of composite slabs with different r’s[1]
图9对比了不同再生粗骨料取代率(r)的钢-混凝土组合板长期挠度试验与预测结果,取代率r分别为0%、50%与100%。3个试件跨度l和厚度d分别为3000 mm 和120 mm,28 d 施加外荷载6.8 kPa。可以看出,本文模型可有效预测不同再生粗骨料取代率的钢-混凝土组合板的长期挠度,r为0%、50%和100%时,28 d 的瞬时挠度分别为1.72 mm、1.95 mm 和2.49 mm,预测结果分别为1.66 mm、1.97 mm 和2.30 mm,预测结果与试验结果分别相差3.0%、0.9%与7.7%;268 d 时跨中挠度实测结果分别为7.42 mm、8.78 mm 和9.83 mm,预测结果分别为6.96 mm、8.46 mm 和10.40 mm,预测值与试验值分别相差6.2%、3.6%和1.9%。
2.2 两跨连续钢-混凝土组合板长期性能预测结果
图10对比分析了两跨连续钢-普通混凝土组合板在不同荷载等级下的长期挠度试验结果与预测结果,组合板单跨跨度l、宽度b和厚度d分别为3300 mm、1200 mm 和150 mm,8 d 分别施加外荷载0 kPa、3.1 kPa 和5.6 kPa,中支座顶部配置长度为2000 mm 的6 10纵向钢筋和长度为1120 mm的7 6横向钢筋。可以发现,CLT-70-3与CLT-70-6试件在8 d 的瞬时挠度分别为0.57 mm 和0.93 mm,预测值为0.30 mm、0.60 mm,预测值比实测值分别小0.27 mm 和0.31 mm。Gholamhoseini 等[27]在进行数值模拟时也发现了同样的问题,作者认为试验所得8 d 瞬时挠度明显超出合理范围,可能由支座虚位移导致。除此之外,8 d~348 d 的长期挠度预测结果较为准确(见图10)。
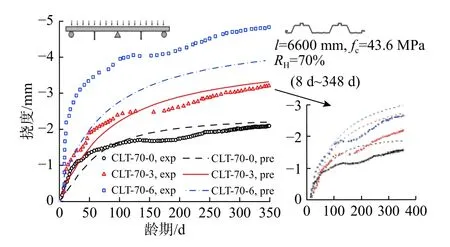
图10 不同荷载等级的两跨组合板挠度试验与有限元结果对比[27]Fig.10 Comparison between measured and numerical timedependent deflectionsof double-span compositeslabs with different loading levels[27]
试件CLT-70-0、CLT-70-3和CLT-70-6在348 d的跨中挠度试验值分别为2.09 mm、3.21 mm 和4.83 mm,预测值分别为2.20 mm、3.31 mm 和3.92 mm,两者分别相差5.1%、3.3%和18.9%。需要说明的是,本文有限元模型中采用试验过程的平均相对湿度,而实际湿度变化存在一定范围的波动,由此引起试件CLT-70-0与CLT-70-3的长期性能预测值与试验值最大相差15.0%与5.6%。
本文同时对两跨连续钢-混凝土组合板在外荷载、收缩和徐变共同作用下的支座弯矩进行了预测,对比结果见图11。服役龄期为348 d 时,试件CLT-70-0、CLT-70-3及CLT-70-6的弯矩实测值分别为19.5 kN·m、18.5 kN·m 和23.4 kN·m,预测值分别为25.4 kN·m、27.8 kN·m 和29.8 kN·m,与试验值分别相差23.2%、33.4%与21.5%。在原文献试验中,试件CLT-70-3在荷载3.1 kPa 作用下的长期支座弯矩均小于试件CLT-70-0(0 kPa)与CLT-70-6(5.6 kPa)的长期支座弯矩,这也一定程度上反映出长期试验中数据测量的离散性。
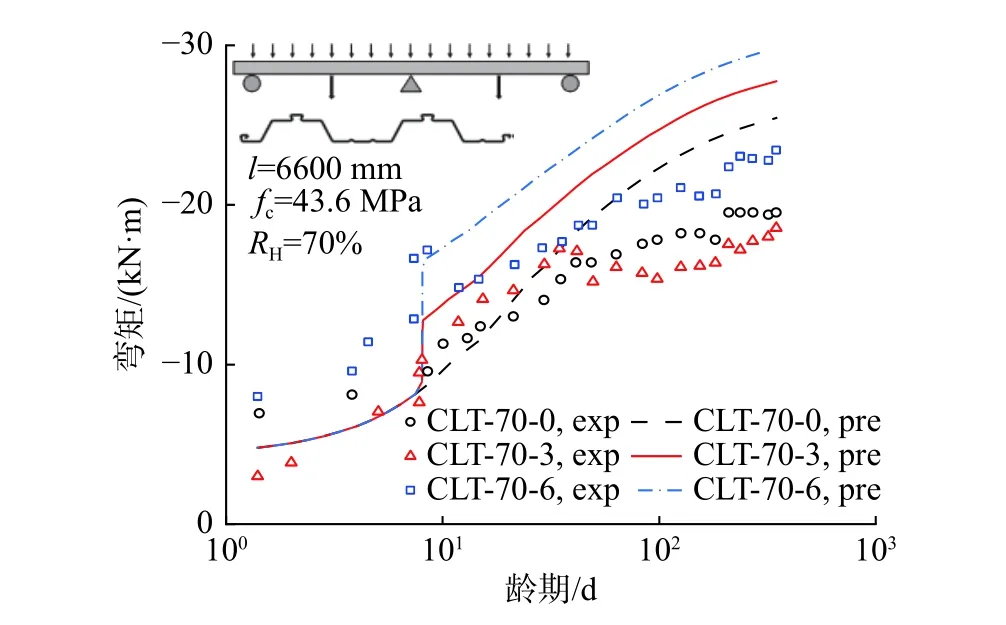
图11 不同荷载等级的两跨组合板弯矩试验与有限元结果对比[27]Fig.11 Comparison between measured and numerical timedependent moments of double-span composite slabs with different loading levels[27]
3 典型设计方法的适用性评述
由于早期缺少系统的钢-混凝土组合板长期性能试验数据,个别规范基于少量试验结果,认为由于压型钢板的存在阻碍了混凝土内部自由水分的散失,进而降低了混凝土的干燥收缩[35],因此建议通过布置配筋率为0.075%的分布钢筋来抵抗混凝土收缩变形的不利影响。但图7中的有限元结果表明,与未配置分布钢筋的组合板相比,配置5 16分布钢筋的组合板(配筋率为0.62%)长期挠度仅降低22.8%。这说明,仅靠构造措施(例如,配置板顶分布钢筋)不能充分降低混凝土收缩变形的影响,仍需要结合计算得到由收缩变形引起的组合板附加挠度。
部分设计规范中通过折减混凝土弹性模量来考虑混凝土长期收缩、徐变的综合影响。例如,我国《组合楼板设计与施工规范》[6]沿用欧洲EC4规范[36]的建议,长期荷载作用下的混凝土弹性模量Ee采用28 d 瞬时弹性模量Ec的50%。考虑到压型钢板对组合板受弯刚度的贡献,采用该措施得到的组合板长期总挠度应小于组合板瞬时挠度的2倍。美国ACI 318规范[35]也建议根据受压区钢筋配筋率ρ′、持荷时间t来计算组合板长期附加挠度δcs(长期收缩和徐变引起)和长期总挠度δtot:
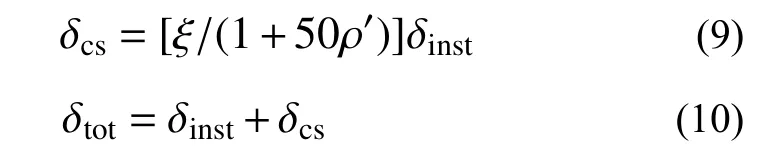
式中:ξ 为长期持荷系数,持荷龄期为0.5年、1年和5年时分别采用1.2、1.4和2.0;ρ′为受压区钢筋配筋率;δinst、δcs和δtot分别为组合板的瞬时挠度、长期收缩徐变引起的附加挠度和长期总挠度。
由于前文大部分试验未给出组合板自重引起的瞬时挠度及对应的徐变挠度,表2列出了文献[3]和文献[1]中混凝土各变形组成导致的组合板挠度,包括总挠度δtot、瞬时挠度δinst、收缩挠度δsh和徐变挠度δcr。可以发现:1)5个试件的总挠度δtot为瞬时挠度δinst的3.54倍~4.30倍,远超过中国和欧洲规范的推荐值(小于2.0),这说明,仅对混凝土弹性模量进行折减,并不能合理预测组合板的长期挠度;2)5个试件由混凝土收缩和徐变 引 起 的 长 期 挠 度δcs(δcs=δsh+δcr)为 瞬 时 挠 度δinst的2.54倍~3.30倍,而采用美国ACI 规范预测公式得到的推荐值为1.30,仅为试验结果的30.2%~51.1%,这也充分说明需要考虑混凝土长期收缩变形对组合板挠度的影响;3)再生粗骨料取代率对组合板长期总挠度δtot的影响显著,与普通混凝土组合板相比,取代率为50%和100%的再生混凝土组合板挠度增大21.7%和38.5%。但不同取代率下,组合板长期挠度δcs与瞬时挠度δinst的比值较为接近(r=0%、50%和100%时,δcs/δinst分别为3.19、3.30和3.19)。
4 考虑荷载分布时取代率对多跨连续组合板长期性能的影响
实际工程应用中,钢-混凝土组合板一般为多跨连续构件(见图1),当组合板的跨数超过5跨,且各跨截面、跨度和受荷相差不大时,计算时可简化为5等跨钢-混凝土组合板[35]。由于本文有限元模型可有效预测单跨钢-普通混凝土组合板、单跨钢-再生混凝土组合板以及两跨连续钢-普通混凝土组合板的长期性能,本文拟通过有限元模拟,研究多跨连续钢-再生混凝土组合板的长期性能。

表2 混凝土的变形组分引起的组合板挠度Table 2 Deflection componentsdue to concretestrain over time
有限元模型中组合板厚度d和单跨跨度l分别为120 mm 和3000 mm,钢板采用典型的KF70压型钢板,组合板顶部设置4组直径16 mm 的纵向分布钢筋(见图2),压型钢板和钢筋的屈服强度fy均为550 MPa,弹性模量Es均为206 GPa;普通和再生混凝土均采用C30强度等级,抗压强度标准值为30 MPa,再生粗骨料取代率采用0%、50%及100%;环境相对湿度和温度分别为60%和20℃;组合板混凝土标准养护28 d 后承担长期荷载作用,持荷时间为50 a,荷载分布参考文献[35](见图12),非均布荷载布置1和2用于确定组合板跨中的峰值挠度,非均布荷载布置3和4用于确定支座的峰值弯矩,均布荷载布置5用于对比分析。

图12 均布荷载及非均布荷载布置示意图Fig.12 Uniformly and non-uniformly distributed loading
4.1 再生粗骨料取代率对长期挠度的影响
图13给出了不同荷载分布下组合板长期挠度,再生粗骨料取代率r分别为0%、50%和100%,可以发现,荷载的瞬时及长期作用下,五跨连续组合板的峰值挠度均出现在第一跨。表3同时列出了典型服役龄期下组合板的长期挠度,可以发现,再生粗骨料的掺入显著增大了组合板挠度。均布荷载作用下(荷载布置5),r=0%、50%和100%的组合板在28 d 的峰值挠度分别为0.97 mm、1.06 mm 和1.17 mm,r增大(50%和100%)对挠度值影响分别为9.4%和20.6%;r=0%、50%和100%的组合板50 a 峰值挠度分别为4.43 mm、5.41 mm 和6.42 mm,r增大(50%、100%)对挠度值影响分别为22.1%、45.0%。当采用非均布荷载形式时(荷载布置1~荷载布置4),r=0%、50%和100%的组合板28 d 峰值挠度分别为1.17 mm、1.28 mm 和1.42 mm,r的增大(50%和100%)对挠度影响分别为9.4%和20.1%;r=0%、50%和100%的组合板50 a 的峰值挠度分别为4.80 mm、5.83 mm 和6.59 mm,r增大(50%和100%)对挠度值影响分别为21.6%和37.4%。

图13 不同荷载布置下连续组合板长期挠度Fig.13 Long-term deflection of continuous composite slabs under different load distributions
由图13还可看出,考虑荷载分布形式将增大组合板的峰值挠度。当采用取代率为0%、50%和100%的组合板承受外荷载作用时,考虑非均布荷载的组合板瞬时峰值挠度比均布荷载工况分别增加20.6%、20.7%和21.4%。但随着服役龄期的增加,该比例逐渐降低,采用取代率为0%、50%和100%的组合板承受50 a 长期荷载作用时,考虑非均布荷载的组合板峰值挠度比均布荷载工况分别增加8.3%、7.7%和2.6%。分析认为,组合板收缩挠度δsh占长期总挠度δtot的比重较大,因此随服役龄期的增加,组合板瞬时挠度δinst及徐变挠度δcr所占的比重逐渐降低。
长期持荷系数可以综合反映收缩和徐变引起放入附加挠度与瞬时挠度的差异(见式(9)),基于此,图14对比了多跨连续钢-再生混凝土组合板长期持荷系数ξ 有限元结果及基于ACI318规范计算结果,可以发现,ACI318规范显著低估了多跨连续钢-混凝土组合板长期持荷系数ξ。以持荷50 a的分析结果为例,采用ACI规范得到的预测结果为2.0,而采用均布荷载的钢-再生混凝土组合板长期持荷系数分别为3.57(r=0%)、4.10(r=50%)和4.49(r=100%);采用非均布荷载时,再生混凝土组合板长期持荷系数分别为3.10(r=0%)、3.55(r=50%)和3.64(r=100%)。基于上述数据,可初步得到与钢-普通混凝土组合板长期性能预测精度相似的钢-再生混凝土组合板长期性能预测公式:

式中,ξ 和ξ′分别为规范和修正的长期持荷系数。
4.2 再生粗骨料取代率对支座负弯矩的影响
图15对比了不同荷载分布下的组合板长期弯矩,再生粗骨料取代率r分别为0%、50%和100%。荷载的瞬时及长期作用下,五跨连续组合板的峰值负弯矩均出现在第二个支座处。表3也列出了典型服役龄期下组合板的长期支座弯矩,可以发现,再生骨料取代率r对组合板支座负弯矩的影响有限,当荷载均匀布置时(荷载布置5),r=0%、50%和100%的组合板28 d 峰值负弯矩均为5.7 kN·m;组合板50 a 的峰值负弯矩分别为12.6 kN·m、13.2 kN·m 和13.9 kN·m,r增大(50%和100%)对弯矩值影响分别为5.2%和10.7%。
当采用非均布荷载时(荷载布置1~荷载布置4),r=0%、50%和100%的组合板28 d 峰值负弯矩分别为6.02 kN·m、6.04 kN·m 和6.05 kN·m,r增大(50%和100%)对弯矩值影响分别为0.2%和0.5%;组合板50 a 峰值负弯矩分别为12.8 kN·m、13.5 kN·m 和14.2 kN·m,r增大(50%和100%)对弯矩值的影响分别为5.3%和10.8%。
与均布荷载工况相比,考虑非均布荷载时的组合板峰值负弯矩增加幅度有限。采用取代率为0%、50%和100%的组合板承受外荷载作用时,考虑非均布荷载的组合板瞬时峰值负弯矩比均布荷载工况分别增加5.99%、6.34%和6.51%。但随着持荷龄期的增加,该比例逐渐降低,采用取代率为0%、50%和100%的组合板承受50 a 长期荷载作用时,考虑非均布荷载的组合板峰值支座负弯矩比均布荷载工况分别增加1.91%、1.97%和2.01%,原因与挠度分析时一致。

表3 不同荷载分布时粗骨料取代率对组合板长期性能的影响Table 3 Influenceof RCA r ratio on long-term performance of composite slabs under different load distributions

图14 长期持荷系数的对比结果Fig.14 Comparison of long-term loading coefficients

图15 不同荷载布置下连续组合板的长期弯矩图Fig.15 Long-term moment figure of continuouscomposite slabs under different load distributions
5 结论
本文基于ABAQUS软件建立组合板的非线性热力耦合有限元模型,基于有限元结果评述现有规范方法的适用性,研究不同荷载分布下再生粗骨料取代率对五跨连续组合板长期性能的影响,得出以下结论:
(1)本文基于龄期调整的有效模量法,建立了钢-再生混凝土组合板长期性能热力耦合模型,考虑了再生混凝土的非均匀收缩、非均匀徐变以及混凝土开裂的综合影响,通过降温模拟混凝土的收缩和徐变特性;利用收集到的18组足尺试验数据验证本文模型可靠性,所有试件的跨中挠度有限元与试验结果最大相差20.3%。
(2)多跨连续钢-混凝土组合板长期挠度和支座负弯矩均随再生粗骨料取代率的增加而增大,而且掺入再生粗骨料对组合板长期挠度的影响更为显著。均布荷载作用下,与钢-普通混凝土组合板相比,采用再生粗骨料取代率为100%的五跨连续组合板的50 a 峰值跨中挠度和支座负弯矩分别增加45.0%和10.8%。与均布荷载工况相比,考虑非均布荷载时钢-再生混凝土组合板挠度和支座负弯矩均略有增大,幅值在10%以内。
(3)结合组合板有限元模拟结果并基于美国ACI 318规范,提出了考虑再生粗骨料取代率影响的钢-混凝土组合板长期持荷系数的修正公式。
