基于机载LiDAR测深水体波形的漫衰减系数提取方法
2021-03-02亓超周丰年吴敬文宿殿鹏王贤昆阳凡林
亓超,周丰年,吴敬文,宿殿鹏,王贤昆,阳凡林*
( 1.山东科技大学 测绘与空间信息学院,山东 青岛 266590;2.自然资源部海洋测绘重点实验室,山东 青岛 266590;3.长江水利委员会水文局长江口水文水资源勘测局,上海 200136)
1 引言
漫衰减系数(Diffuse Attenuation Coefficient,Kd)是水体的固有光学属性,反映了激光在水体中受散射、吸收所引起的能量衰减变化,是分析海水水质的重要参数之一[1]。漫衰减系数的大小主要取决于水体中的浮游生物含量(叶绿素浓度)、悬浮泥沙含量(浑浊度)、营养盐含量(黄色物质、溶解有机物质、盐度指标)以及其他污染物等因素,研究漫衰减系数可对水体富营养化、水体浑浊度骤增以及水体污染等环境变化实现实时、有效监测,在海洋科学研究、海洋工程应用、海洋渔业研究和海岸带环境监测等方面发挥重要的作用[2–3]。
由于水体的流动性,导致了水中物质的非均匀分布,增加了水体中漫衰减系数的获取难度。目前,国内外针对漫衰减系数的提取主要通过实地测量、被动遥感以及主动遥感3种方式进行。实地测量利用赛克盘和透射计等工具测量水体透明度,进而反演得到漫衰减系数,这些方式需以测量船为载体,效率较低且覆盖范围小,难以快速获取大面积水域的漫衰减系数空间分布[2,4–5];通过卫星遥感影像数据可间接反演漫衰减系数,这种被动遥感方式可对大范围海域的漫衰减系数进行求取,但是无法在云雾天气、夜晚实施测量,且由于卫星设备本身的限制,测量精度难以保证,成果分辨率较低[6–8];全波形机载LiDAR测深(Airborne LiDAR Bathymetry, ALB)技术的出现弥补了上述方法的缺陷,运用水体散射回波的强度变化可实现漫衰减系数的快速反演[4,9–13]。Billard等[9]利用ALB技术在不同深度下的辐照度进行指数拟合,进而反演得到漫衰减系数的方法,该方法需要水底底部回波强度和相应深度信息;Ding等[10]提出了一种基于单波长ALB全波形数据的漫衰减系数计算方法,克服了传统方法的局限性,但未对水体散射回波进行拟合分解,易受噪声影响。
因此,针对目前船载实地测量效率与分辨率低、卫星遥感反演精度与分辨率较低的局限性,本文结合ALB技术高精度、高分辨率、灵活机动、快速高效的特点,提出了一种基于机载LiDAR测深水体波形的漫衰减系数提取方法。ALB原始波形数据经小波去噪之后,利用基于分层异构模型的波形分解算法[14–15](水面−高斯函数、水体−双指数函数及水底−高斯函数)分解得到水体散射回波信号,进而获取大面积水域漫衰减系数的空间分布。
2 基于机载LiDAR测深水体波形的漫衰减系数提取方法
机载LiDAR测深水体波形的漫衰减系数提取方法充分利用了ALB技术高精度、高分辨率、灵活机动、快速高效的独特优势,考虑到激光在水体中的衰减特性以及计算效率,通过分层异构模型的机载LiDAR波形分解算法分解得到水体散射回波信号,并用其与水体散射回波强度方程构建相应模型,用以计算每个激光测深点的漫衰减系数。该算法的步骤为:首先获取机载LiDAR测深原始波形数据,对其进行去噪;然后利用分层异构模型对去噪后的波形数据进行分解,分解得到水体散射回波信号;再通过水体散射回波信号分别计算得到双段指数所对应的初始漫衰减系数;最后根据双段指数的采样时间确定相应权重,对初始漫衰减系数取加权平均,得到该激光测深点最终的漫衰减系数值。本文算法具体流程如图1所示。
2.1 基于分层异构模型的波形分解算法
机载LiDAR测深系统利用具有较强透水能力的蓝绿色波段(532 nm)激光进行探测,其激光接收器能够以数字化的形式记录每个激光脉冲的全部回波波形信号(图2)[15–16],包括水面反射回波、水体散射回波、水底反射回波以及噪声4部分[17],可描述为

式中,t表示时间刻度;fs(t)表示水面反射回波;fc(t)表示水体散射回波;fb(t)表示水底反射回波;fN(t)表示原始波形的噪声;f(t)为t时刻回波的振幅。
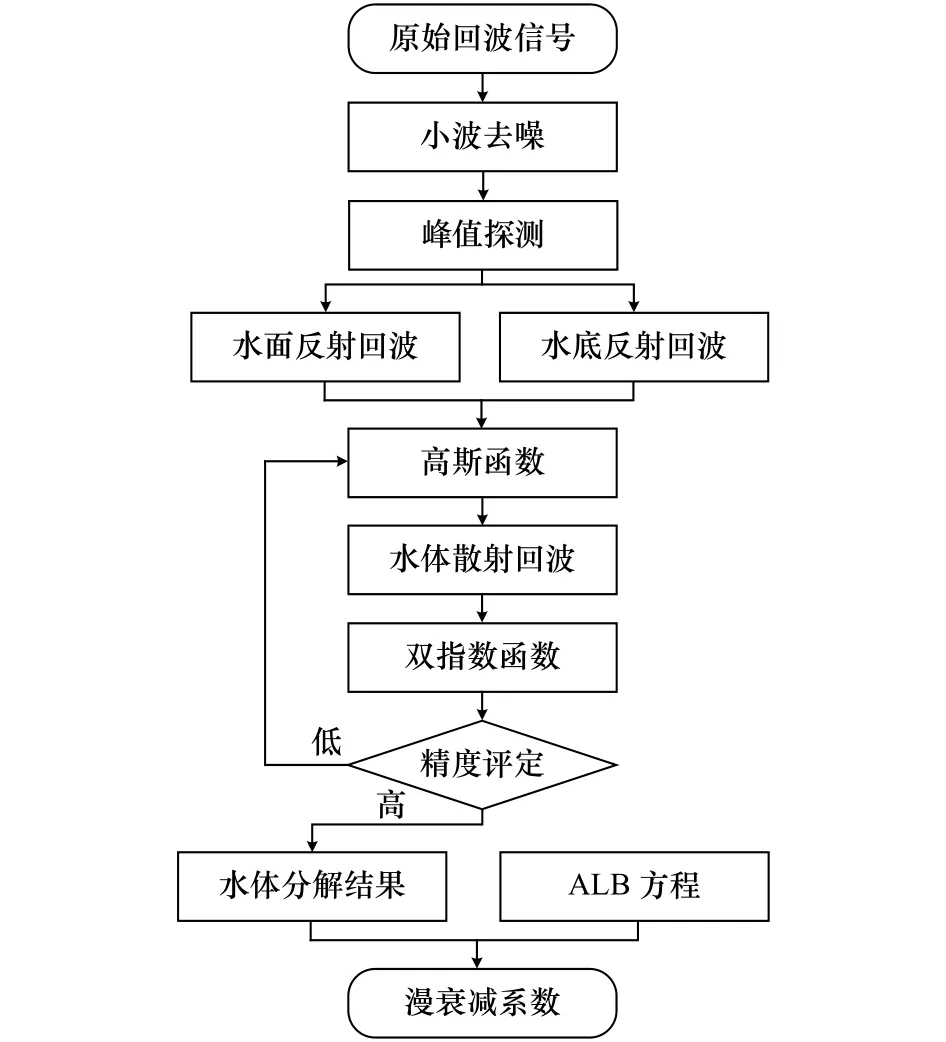
图1 本文方法流程图Fig.1 Flow diagram of the new method in this study
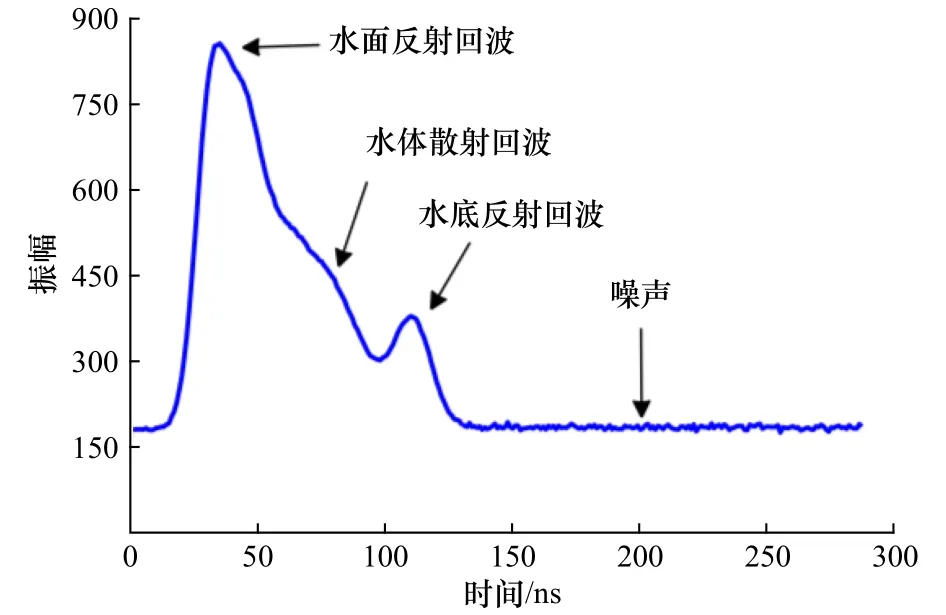
图2 机载LiDAR测深波形示意图Fig.2 Airborne LiDAR bathymetric waveform
其中,噪声包括背景噪声和传感器内部噪声,其存在会导致波形分解函数初始参数估计不准等问题,容易获得含有粗差的波形,影响波形分解精度。因此,在波形分解之前,需对原始回波信号中的噪声进行相应的滤除,文中使用小波算法对噪声进行处理[15,18]。
波形分解是机载LiDAR测深数据处理的重要环节,是漫衰减系数提取的基础。根据机载LiDAR测深回波信号各部分的波形特征,选择合适的函数构建分层异构模型(水面−高斯函数、水体−双指数函数及水底−高斯函数)进行分解,从而将叠加在水面反射回波和水底反射回波中的水体散射回波精确地分解出来,得到水体散射回波所对应的函数。
考虑到ALB系统发射和接收的激光脉冲信号近似服从高斯分布[19–20],因此,根据水面和水底反射回波相应特性分析,文中采用高斯函数(公式(2))分解得到水面、水底反射回波信号,

式中,i表示水面(水底)反射回波信号的分解结果;Ai、μi和σi分别为水面(水底)高斯函数的波峰值、波峰位置和半幅波宽。
从去噪后的ALB波形数据中剔除水面、水底反射回波信号,即可得到初始水体散射回波信号。根据光在水体中辐射传输定理可知,激光在水体中传播时,其脉冲能量随水深的增加而呈现指数衰减。针对水体散射回波的分解,Ding等[21]在三角形函数[22]和四边形函数[23]分解方法的基础之上,提出了一种改进的四边形函数,将水体散射回波下降沿的一段采用指数函数描述。由于水体浑浊度在垂直剖面上非均匀分布导致激光脉冲的衰减程度不同[24],综合激光在水体中衰减特性和分解效率的问题,如图3所示,文中将水体沿垂直剖面分为两层,利用双指数函数ABCD(公式(3))分解得到水体散射回波信号

式中,ax、bx、cx、dx分别表示双指数函数 4 个顶点 (A、B、C、D)的位置时刻;by、cy、dy为 B、C、D的振幅值。
非线性拟合需要预设初值,以降低迭代次数,增加拟合速度。文中遵循非线性最小二乘(Non-linear Least Squares, NLS)方法(公式 (4)),采用 Levenberg-Marquardt算法对13个初始参数(水面–高斯函数3个、水底−高斯函数3个、水体−双指数函数7个)进行迭代优化,直到拟合偏差达到最小为止,以求得各参数的精确值。将优化后的水体反向散射回波参数代入公式(3),得到最优的水体散射回波分解结果,进而用于漫衰减系数的提取。
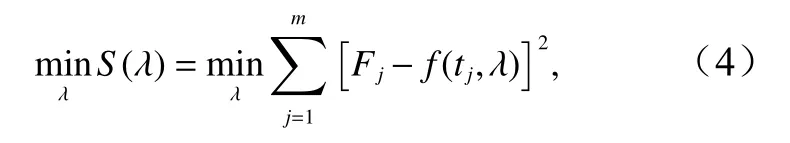

图3 双指数函数分解水体散射回波示意图Fig.3 Decomposition of water column contribution by doubleexponential function
式中,λ表示所求参数;S(λ)表示拟合偏差的平方和;Fj表示波形分解结果在j时刻的振幅。
2.2 漫衰减系数Kd的提取
机载LiDAR测深系统在深度为Di处的水体散射回波强度方程可由下式来描述[4,17]

式中,Di表示水层深度;Pc(Di)表示深度Di时的水体散射回波强度;P表示激光发射强度;表示大气双
e程损失因子;AR表示激光接收器的视场面积;ηe和ηR分别表示激光发射器的光学效率和激光接收器的光学效率;F表示接收视场角损失因子;LS是通过表面传输的损失,即表面反照率;β(ϕ)表示体散射函数;θ表示激光传入水体时的入射角,即天底角;θw表示射入水体后的折射角;nw表示水体折射率;H表示飞机航高;Kd表示532 nm波段处的漫衰减系数;c表示激光在真空的传播速度;ti表示水层深度Di处的时刻;ts表示水面反射回波的峰值位置。
对该方程分析可知,激光脉冲回波强度随水深深度和漫衰减系数增加呈指数衰减,因此,可以通过水体散射回波所对应的双指数函数反演水体的漫衰减系数。文中假设外业测量过程中飞机航高保持稳定,激光发射器的天底角以及接收视场角保持恒定,且所有损耗因素均得到较好的控制,对水体散射回波强度方程进行简化,并将公式(6)代入公式(5),并简化公式(5),得到简化后的水体散射回波强度方程为

由于近岸水深通常小于30 m,与飞机航高H(通常为400~500 m)相比,参数Di对W的影响可以忽略不计,因此,W可认为是一个常数。但是W涉及未知参数太多,不能直接确定。通过分析发现,公式(3)和公式(7)均可描述为如下指数型函数的形式,

式中,y(t)为指数型函数;m、n分别为指数型函数的系数。
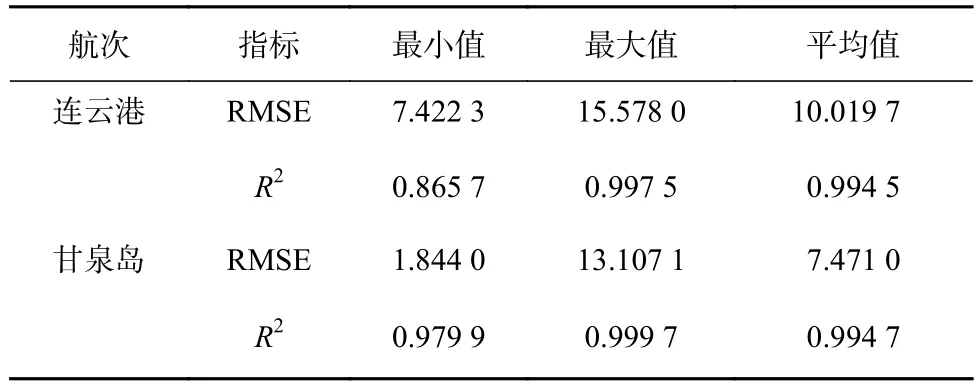
考虑到传统漫衰减系数提取算法所存在的局限性[9–10],结合2.1节中水体散射回波双指数函数(公式(3))与简化后的水体散射回波强度方程(公式(7))构建模型,从而计算漫衰减系数Kd值。以双指数函数(图3)BC段为例,当bx≤t 对公式(9)做方程变换,得到BC段指数所对应的初始漫衰减系数Kd1,同理,计算得到CD段指数所对应的初始漫衰减系数Kd2,如下式所示: 为了保证所得漫衰减系数的准确性,以BC段、CD 段的采样时间(Δt1=cx−bx与 Δt2=dx−cx)确定相应权重,根据公式(12),对Kd1与Kd2取加权平均,得到Kd1与Kd2的加权平均值,将此加权平均值作为该激光测深点最终的漫衰减系数值 为分析所提算法的性能,文中分别应用2013年1月西沙甘泉岛(Optech Aquarius)与2014年12月江苏连云港(Optech CZMIL)两个航次的ALB实验数据,两个航次的测区位置如图4所示。Aquarius和CZMIL均为全波形ALB系统,如表1所示,二者相应的技术参数是不同的。数据采集期间,由于西沙甘泉岛远离大陆,人类活动较少,相比于连云港沿岸海域,甘泉岛海域水质好,海水能见度高。 图4 研究区域位置Fig.4 Location of the study areas 表1 Aquarius与CZMIL的技术参数Table 1 Technical parameters of Aquarius and CZMIL 通过2.1节分解算法分别对西沙甘泉岛和江苏连云港两个航次的ALB波形数据(西沙甘泉岛8 034个,连云港6 011个)进行处理,分别从两个航次的波形处理结果中随机选取一个进行展示,如图5所示。此外,利用分解结果与去噪后的波形数据对比计算得到均方根误差(Root Mean Square Error, RMSE)和确定系数 (Coefficient of Determination,R2)[14–15],从而对文中分解算法性能加以验证,如表2所示。 图5 波形处理结果Fig.5 Waveform processing results 通过对波形去噪结果分析可知,采用小波去噪算法可将西沙甘泉岛和江苏连云港两个航次的原始回波信号中的噪声信号明显地滤除,去噪效果理想。连云港属于高浑浊海域,其ALB波形的水底反射回波较弱,且由于该测区水深较浅,水体散射回波与水面、水底反射回波叠加在一起,导致波形分解的难度变大,由波形分解结果可知,使用文中所提波形分解算法能够将水体散射回波精确地分解出来,其RMSE、R2的平均值分别为10.019 7、0.994 5。西沙甘泉岛周围海域水质较好,ALB最大探测深度相对较深,因而运用文中分解算法处理甘泉岛波形数据的精度相对更高,其RMSE、R2的平均值分别为7.471 0、0.994 7。综上所述,无论是水质清澈的西沙甘泉岛海域,还是较浑浊的江苏连云港沿岸,采用文中所提基于分层异构模型的波形分解算法均能够将叠加在水面反射回波和水底反射回波中的水体散射回波精确地提取出来,得到水体散射回波所对应的函数(双指数函数),为进一步提取漫衰减系数提供了可靠保障。 为验证文中漫衰减系数提取算法的有效性,运用Billard B传统方法[9]与文中算法反演漫衰减系数,并作对比分析。文中以包含实验区域深水和浅水数据为原则,随机在西沙甘泉岛、江苏连云港各选取两个区块内的ALB测深数据,应用上述两种算法进行处理,得到漫衰减系数的平均值如表3。 表2 分解算法性能指标Table 2 Performance indexes of waveform fitting algorithm 表3 漫衰减系数提取结果Table 3 Extraction results of diffuse attenuation coefficient 图6 甘泉岛西南角样本区域空间分布Fig.6 Distribution of the sample area in the Ganquan Island 通过表3分析可见,运用文中算法与传统方法在西沙甘泉岛和江苏连云港海域所得的漫衰减系数平均值相近,证明了利用机载LiDAR测深波形进行漫衰减系数提取算法的可行性。此外,通过表4可知[25],基于文中算法所得漫衰减系数分别反演连云港沿岸和甘泉岛海域的水质情况,显示出了较好的区分度。 表4 漫衰减系数与水质之间的关系[25]Table 4 Relationship between diffuse attenuation coefficient and water quality[25] 为进一步验证文中算法的可行性,文中选择西沙甘泉岛西南角沿岸作为样本区域(图6a),利用其ALB数据进行处理,并生成该区域漫衰减系数空间分布图(图6c)与频率分布直方图(图7)、相应水深的空间分布图(图6b)。 通过图6和图7可知,运用文中算法所得漫衰减系数的分布规律与该海域相应水深的分布规律基本保持一致,即当甘泉岛沿岸水越来越来深时,漫衰减系数会越来越小;该区块漫衰减系数主要集中在0~0.5 m−1,其平均值为 0.215 6 m−1。浅水处由于潮水的作用,海水会对海底底质产生冲刷,大量泥沙等底质在水中悬浮,因此,浅水处漫衰减系数较高;随着水深的增加,海底底质受潮水的冲刷作用减弱,漫衰减系数逐渐变小。此外,文中还绘制了连云港区块A的漫衰减系数频率分布直方图(图8),结果表明,该区域漫衰减系数主要集中在0.3~0.7 m−1,其平均值为 0.378 8 m−1。 综上所述,文中利用ALB测深水体波形提取漫衰减系数的算法具有较强可行性和适应性,可有效提取每一个激光测深点的漫衰减系数。 结合ALB技术高精度、高分辨率、灵活机动、快速高效的特点,提出了一种基于机载LiDAR测深水体波形的漫衰减系数提取方法。通过分析ALB波形数据,针对水面、水体及水底3部分回波的相应特性,构建分层异构模型,分离得到混叠在水面回波和水底回波之间的水体后向散射回波,进而利用所得水体后向散射回波实现大面积水域漫衰减系数空间分布的精确获取,为快速、精细化分析大面积水域的水体环境变化提供了一种新的解决方案。

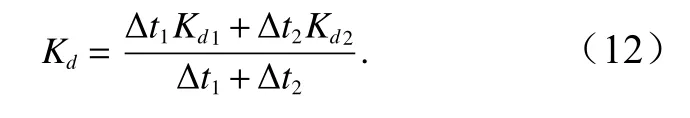
3 实验与分析


3.1 波形分解结果
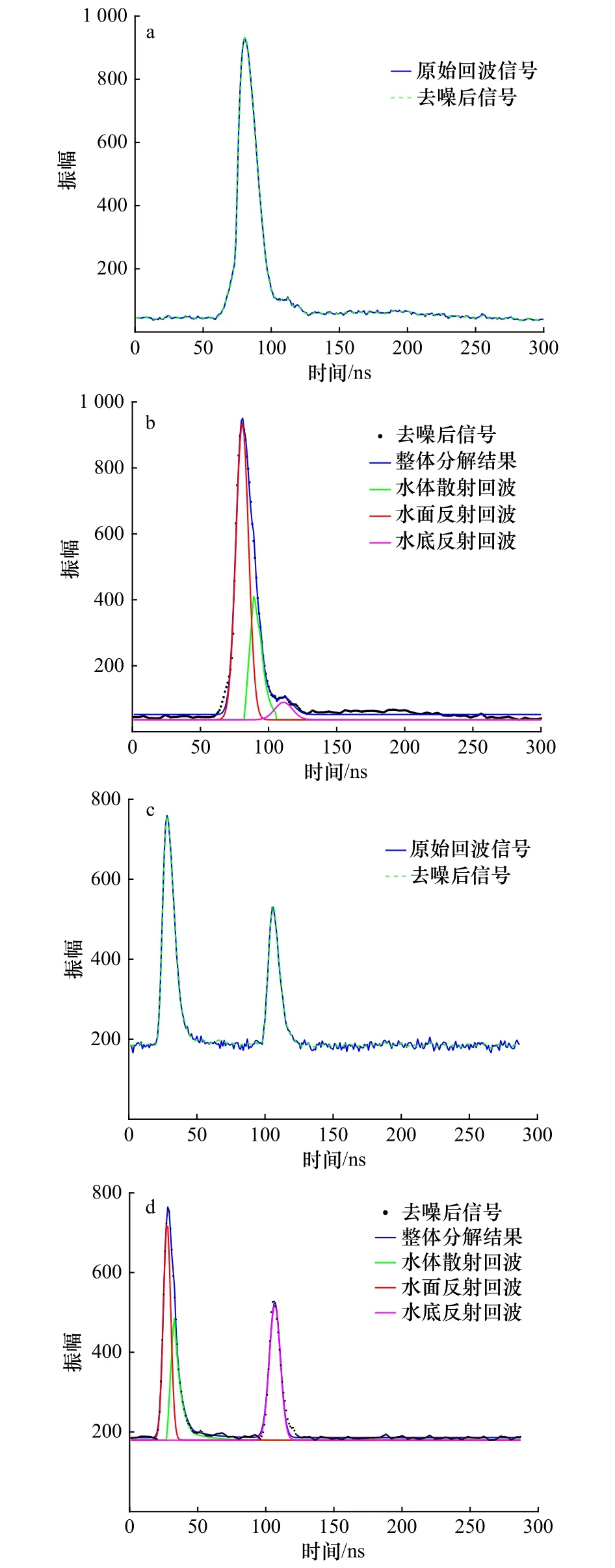
3.2 漫衰减系数提取结果



4 结论

