基于Himawari-8卫星的逐时次海表温度融合

周旋，叶小敏，周江涛，杨晓峰

( 1.中国人民解放军61741部队，北京 100094；2.国家卫星海洋应用中心，北京 100081；3.中国科学院空天信息创新研究院 遥感科学国家重点实验室，北京 100101)

1 引言

海表温度是研究海气界面物质和能量交换的一个重要地球物理参数，在气候变化研究中起着重要的作用。它表征海洋的热力与动力过程，并受到海洋与大气相互作用的影响，为研究海洋环流、中尺度涡、海洋锋、上升流和海水混合等海洋现象提供了重要依据。获取高频次、高空间分辨率、高精度、全覆盖的海表温度对于研究海气相互作用、海洋热动力过程和气候变化具有重要意义。Himawari-8卫星是日本气象厅于日本时间2014年10月7日发射的新一代地球同步静止气象卫星，搭载了高级Himawari成像仪（AHI）。它的观测频率为10 min一次，具有16个光谱通道，红外通道的空间分辨率达到2 km，其海表温度产品具有较高的时空分辨率，在西北太平洋海表温度遥感监测方面具有明显的优势，但同时由于云雾的遮挡，空间覆盖受到较大的影响。本文以Himawari-8卫星红外遥感海表温度产品为基础，融合东北亚区域海洋观测系统（NERA-GOOS）现场观测资料和地球水环境变化监测卫星高级微波扫描辐射计（GCOM-W1 AMSR2）微波遥感海表温度产品，弥补红外遥感海表温度空间覆盖的不足，生成高频次、高空间分辨率、高精度、全覆盖的西北太平洋海表温度融合产品，满足海气相互作用、海洋热动力过程和气候变化等研究的需求。

常用的海表温度融合处理算法包括最优插值、变分分析和卡尔曼滤波。最优插值最早由Eliassen等[1]提出，是在假定背景值、观测值和分析值均为无偏估计的前提下，求解分析方差最小化的一种分析方法。Reynolds等[2–5]将其应用到卫星遥感和船舶、浮标观测的全球海表温度融合，取得了较好的效果。变分分析通过最小化目标函数求得全局最优分析解[6]，是最优插值的一般化，可以用来处理观测矩阵是非线性的情况，其计算量要比最优插值大。卡尔曼滤波最初由Kalman[7]提出，其在线性系统、高斯白噪声以及高斯先验分布的假定条件下，通过最小化分析误差得到最优解。最优插值亦是卡尔曼滤波的简化版，但是卡尔曼滤波计算量大，并占用大量机器内存，同时很难估计模型误差。由于最优插值实现上的简单性、计算代价的合理性，本文选择最优插值实现Himawari-8 AHI海表温度、GCOM-W1 AMSR2海表温度和NERAGOOS现场观测资料的融合。

海表温度的日变化和多源海表温度间的系统偏差是影响逐时次海表温度融合产品精度的两个重要因素。本文利用Himawari-8 AHI海表温度和欧洲中期天气预报中心（ECWMF）海面风速数据，结合太阳辐照度的日变化特征，研究分析海表温度随风速和太阳辐射的日变化情况，建立Himawari-8 AHI海表温度日变化模型，实现海表温度的日变化订正；然后以Himawari-8 AHI海表温度为目标数据，利用泊松方程对GCOM-W1 AMSR2海表温度进行偏差订正，消除多源海表温度间的系统偏差；最后，从融合产品个例分析和精度检验两个方面评价逐时次海表温度融合产品。

2 数据准备和预处理

2.1 Himawari-8 AHI海表温度

Himawari-8卫星位于140.7°E的地球静止轨道，观测范围为 60°S～60°N，80°E～160°W，搭载了 AHI成像仪，具有3个可见光通道、3个近红外通道和10个红外通道，全圆盘数据的时间分辨率为10 min一次。日本宇宙航空研究开发机构（JAXA）发布了Himawari-8 AHI海表温度，包括2级和3级产品，时间分辨率分别为10 min和1 h，空间分辨率均为2 km。与传统的劈窗算法不同，该产品采用准物理算法，利用8.6 μm、10.4 μm和11.8 μm红外通道数据求解参数化的红外辐射传输方程反演提取海表温度，达到较高的精度[8]。本文选用3级Himawari-8 AHI海表温度产品作为基础数据源，逐时次融合GCOM-W1 AMSR2和现场测量海表温度。

由于云的辐射特性比较复杂，在许多情况下很难将一些区域明确划分为晴空或云覆盖，而这些区域的Himawari-8 AHI海表温度存在较大误差。为了保证海表温度融合产品的精度，在融合之前需要对Himawari-8 AHI海表温度产品进行质量控制，剔除异常数据，提高产品可信度。

2.1.1 气候态值检验

同一海区、同一时期的海表温度相对稳定、变化较小，利用海表温度气候均值并结合其变化量可以对Himawari-8 AHI海表温度进行检验，剔除异常数据。利用英国气象局发布的1992–2010年业务海表温度和海冰分析产品（OSTIA）计算每天的海表温度均值和均方差，并插值到Himawari-8 AHI海表温度产品的网格点上，其中海表温度均值作为气候态值，2.5倍均方差作为临界值。当Himawari-8 AHI海表温度与气候态值差的绝对值大于临界值，认为该数据异常，将其剔除。

2.1.2 空间一致性检验

海表温度在空间上变化比较缓慢，一定空间范围内海表温度的均方差较小。对于Himawari-8 AHI海表温度的每个格点，计算以其为中心5×5窗口的均值和均方差。在完全晴空下，5×5窗口的海表温度均方差较小；当受到云干扰时，均方差增大。当格点值与均值之差大于2.5倍均方差时，认为该数据异常，将其剔除。

2.1.3 时间一致性检验

同一位置的海表温度在时间上变化比较缓慢，一定时间范围内单个格点海表温度的均方差较小。对于Himawari-8 AHI海表温度的每个格点，计算前5 d时间范围内的均值和均方差。在晴空下，均方差主要反映海表温度的日变化，其值较小；当受到云干扰时，均方差明显增大。本文将格点值与均值之差大于2.5倍均方差的格点进行剔除。

2.2 GCOM-W1 AMSR2海表温度

AMSR2是搭载在GCOM-W1卫星的微波辐射计，以偏离星下点55°进行圆锥扫描，幅度为1 450 km，升交点时间为13:30，工作频率为6.925 GHz、7.3 GHz、10.65 GHz、18.7 GHz、23.8 GHz、36.5 GHz和 89.0 GHz，每个频率包括水平和垂直两个极化通道。JAXA发布了10 km和25 km的GCOM-W1 AMSR2海表温度产品，包括沿轨和网格化两种类型。该产品利用6.925 GHz垂直极化通道数据反演海表温度，具有全天时、全天候的特点，具有较高的精度[9]。本文选用空间分辨率为25 km的沿轨GCOM-W1 AMSR2海表温度产品进行融合。

GCOM-W1 AMSR2海表温度受降雨影响较大，在融合之前，根据质量标识剔除受降雨影响的数据，然后重投影到10 km分辨率的网格上，对每个网格点进行气候态值检验、空间一致性检验和时间一致性检验以保证其精度，最后通过双线性插值到2 km分辨率的网格上。

2.3 NERA-GOOS现场观测资料

NERA-GOOS是全球海洋观测系统的东北亚区域试验项目，其现场观测资料的来源主要有固定浮标、漂流浮标、沿岸站、海洋科学考察船和自动观测船。NERA-GOOS数据库包括区域实时数据库（RRTDB）和区域延时数据库（RDMDB），RRTDB用于存放最近30 d的数据，30 d以上的数据迁移到RDMDB。本文采用RDMDB中全球海表温度和盐度解码数据。

由于NERA-GOOS现场观测资料存在较大的误差，在融合之前，需要进行必要的质量控制，剔除异常的数据，主要包括浮标编号、船号、时间记录和经纬度不合格的数据以及记录错误的数据。

3 海表温度融合方法

高空间覆盖度、高空间分辨率、逐时次的海表温度融合产品对于研究海洋环流、中尺度涡、海洋锋、上升流和海水混合等海洋现象具有重要意义。本文以3级Himawari-8 AHI海表温度为基础，融合GCOM-W1 AMSR2海表温度产品和NERA-GOOS现场观测资料，生成逐时次的西北太平洋海表温度融合产品。具体融合流程如图1所示。

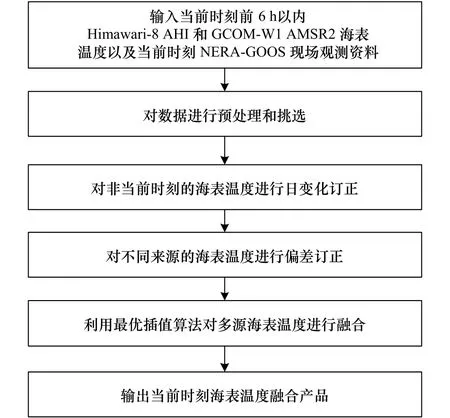
图1 海表温度融合流程Fig.1 The flow of sea surface temperature fusion

首先，为了提高海表温度遥感观测资料的空间覆盖度，选择当前时刻前6 h以内Himawari-8 AHI和GCOMW1 AMSR2海表温度产品以及当前时刻NERA-GOOS现场观测资料作为融合数据源，并对数据进行预处理和挑选；其次，考虑到海表温度存在日变化，研究建立Himawari-8 AHI海表温度日变化模型，实现对非当前时刻海表温度的日变化订正；然后，由于多源海表温度间存在系统偏差，以Himawari-8 AHI海表温度为目标数据，利用泊松方程对GCOM-W1 AMSR2海表温度进行偏差订正；最后，利用最优插值法实现Himawari-8 AHI海表温度、GCOM-W1 AMSR2海表温度和NERA-GOOS现场观测资料的逐时次融合。

3.1 数据挑选

当前时刻前6 h以内Himawari-8 AHI和GCOMW1 AMSR2海表温度产品存在重复观测的区域，即同一个网格点上存在多个观测数据，因此，在融合之前需要对重复观测数据进行挑选。本文按照海表温度产品的种类和时间先后顺序挑选数据。首先，比较海表温度产品的种类，由于Himawari-8 AHI海表温度产品的空间分辨率高于GCOM-W1 AMSR2海表温度，其优先级高于GCOM-W1 AMSR2；然后，比较距离当前时刻的远近，距当前时刻近的数据优先级要高。

3.2 日变化订正

由于太阳辐射作用，海表温度存在日变化。融合数据源为当前时刻前6 h以内海表温度，由于邻近时刻的海表温度与当前时刻存在差异，为了保证融合产品精度，需要建立海表温度日变化订正模型，将邻近时刻的海表温度订正到当前时刻。Gentemann等[10]利用AVHRR红外传感器开拓者海表温度和TMI微波传感器海表温度数据建立了随时间、风速和太阳辐射变化的日变化经验模型。与AVHRR海表温度和TMI海表温度不同，Himawari-8 AHI海表温度产品的时间分辨率优于1 h，在研究海表温度日变化规律方面具有独特的优势。本文在Gentemann等[10]模型基础上研究建立Himawari-8 AHI海表温度日变化模型。

海表温度日变化为卫星遥感海表温度与夜间参考海表温度的差。为了避免个别受云污染的网格点所带来的误差，夜间参考海表温度取地方时03:00至07:00海表温度的平均值。图2为2017年10月5日8.04°N，143.00°E海表温度日变化样例图，其中1天中的海表温度低值集中在03:00至07:00，海表温度高值集中在12:00至14:00。

为了建立海表温度日变化模型，本文选择2017年1月、4月、7月和10月的Himawari-8 AHI海表温度以及ECWMF海面风速数据研究分析海表温度日变化随风速和太阳辐射的变化情况。ECWMF海面风速的时间分辨率为6 h，空间分辨率为25 km，通过双线性插值到Himawari-8 AHI海表温度网格。太阳辐照度是纬度和时间的函数，采用Liou[11]的公式计算。不同风速条件下海表温度日变化幅度随太阳辐照度的变化情况如图3所示，不同太阳辐照度条件下海表温度日变化幅度随海面风速的变化情况如图4所示。

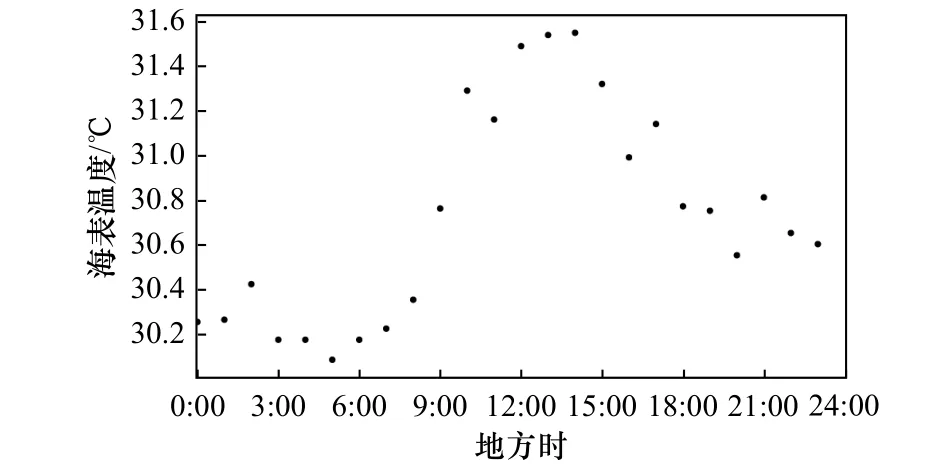
图2 海表温度日变化情况（以2017年10月5日8.04°N，143.00°E 海表温度变化为例）Fig.2 The daily variation of sea surface temperature at 8.04°N, 143.00°E on October 5, 2017

由图3和图4可知，匹配数据主要集中在海面风速1～4 m/s和太阳辐照度420～500 W/m2范围内。当风速一定时，随着太阳辐射的增强，海表温度日变化幅度增大，二者近似线性变化关系；当太阳辐射一定时，随着风速的增加，海表温度日变化幅度减小，二者近似指数变化关系。

利用最小二乘法对海表温度日变化幅度与海面风速、太阳辐照度的变化关系进行拟合（如图3和图4的蓝色直线）：

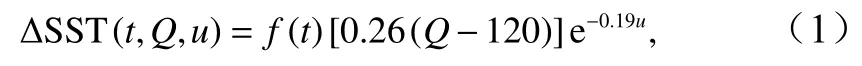
式中，t为时间；Q为太阳辐照度；u为海面风速；f(t)为海表温度日变化因子，采用Gentemann[10]的公式计算，w为常数0.266 8：

在融合之前，需要将邻近时刻的海表温度订正到当前时刻。将时间、海面风速和太阳辐照度带入式（1），计算邻近时刻与当前时刻海表温度的差异，进而实现邻近时刻Himawari-8和AMSR2海表温度的日变化订正。

3.3 海表温度偏差订正

由于探测机理、传感器性能和反演算法等方面的差异，Himawari-8 AHI海表温度和GCOM-W1 AMSR2海表温度存在系统偏差，如图5a和图6a所示，在过渡区域形成明显的拼接缝。为了保证融合产品的精度，在融合之前需要对多源海表温度进行偏差订正，消除系统偏差。本文以Himawari-8 AHI海表温度为目标数据，利用泊松方程对GCOM-W1 AMSR2海表温度进行偏差订正，其基本思想是改变AMSR2海表温度的梯度场以获得一个新的梯度场，并通过最小化该梯度场与Himawari-8 AHI海表温度的梯度场v差异来实现，即

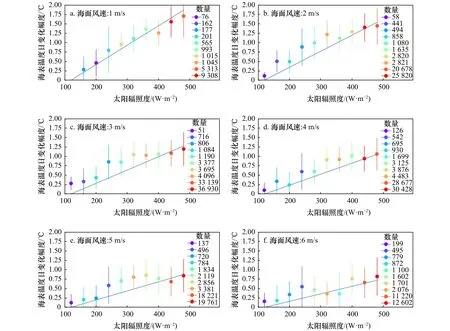
图3 海表温度日变化幅度随太阳辐照度的变化Fig.3 The amplitude of diurnal sea surface temperature variation with solar irradiance

式中，f为偏差订正后的GCOM-W1 AMSR2海表温度；f∗为Himawari-8 AHI海表温度；为梯度算子；∥ ∗∥表示向量 ∗的L2范数；Ω为GCOM-W1 AMSR2海表温度覆盖区域；∂ Ω为GCOM-W1 AMSR2海表温度与Himawari-8 AHI海表温度的拼接区域；f|∂Ω和表示 ∂ Ω区域的海表温度。偏差订正后的GCOM-W1AMSR2海表温度和Himawari-8 AHI海表温度的梯度差异采用图像的L2范数表示。由欧拉–拉格朗日方程，式（3）变成满足狄利克雷边界条件的泊松方程[12–14]：

图4 海表温度日变化幅度随海面风速的变化Fig.4 The amplitude of diurnal sea surface temperature variation with wind speed

图5 Himawari-8 AHI和 GCOM-W1 AMSR2 海表温度的拼接产品（28.8°～31.2°N，123.2°～126.2°E）Fig.5 The mosaic sea surface temperature from Himawari-8 AHI and GCOM-W1 AMSR2 at 28.8°−31.2°N and 123.2°−126.2°E

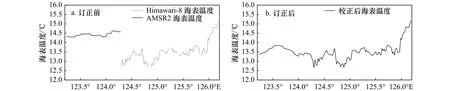
图6 Himawari-8 AHI和GCOM-W1 AMSR2海表温度的拼接产品（29.8°N）Fig.6 The mosaic sea surface temperature from Himawari-8 AHI and GCOM-W1 AMSR2 at 29.8°N

图5为Himawari-8 AHI和GCOM-W1 AMSR2海表温度拼接产品的样例图，空间范围为28.8°～31.2°N，123.2°～126.2°E，时间为2017年4月3日18:00；图6为沿 29.8°N线的 Himawari-8 AHI和 GCOM-W1 AMSR2海表温度，经度范围和时间与图5一致。由图5a和图6a可知，订正前，由于Himawari-8 AHI海表温度和GCOM-W1 AMSR2海表温度存在系统偏差，产生明显的拼接缝。本文以Himawari-8 AHI海表温度为目标数据，通过泊松方程对GCOM-W1 AMSR2海表温度进行偏差订正。由图5b和图6b可知，订正后，Himawari-8 AHI海表温度和GCOM-W1 AMSR2海表温度之间的拼接缝消失，取得了较好的效果。

3.4 最优插值融合

海表温度经过日变化订正和偏差订正后，本文利用最优插值法实现海表温度逐时次融合。最优插值法是在假定初估值、观测值和分析值均为无偏估计的前提下，求解分析值误差方差最小的一种客观分析方法。在最优插值法中，空间网格点的分析值是由网格点的初估值加上订正值而确定的，其订正值由周围各观测点的观测值与初估值的偏差加权求得：

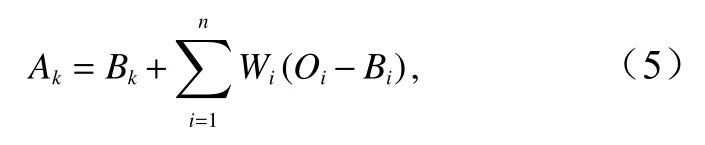
式中，k为分析格点；i为观测格点；Ak代表在网格点k上的分析值，即海表温度最优插值的融合结果；Bk代表网格点k上的初估值，这里选择前一时次融合的海表温度加上当前时次海表温度增量；Wi代表权重函数；Oi为 代表在网格点i上的观测值。

为了分析值误差方差最小，Wj应满足:

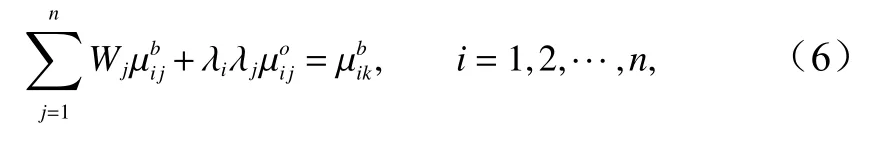
式中，j表示位于观测/网格点i周围的观测/网格点，为初估场误差协相关；为观测场误差协相关，假定网格点之间的观测误差相互独立，则当i等于j时为1，当i不等于j时为0；εi为i点上观测场误差标准差和初估场误差标准差的比率，采用Reynolds和Smith[2]的取值方法。空间网格点上分析值的最小误差估计为

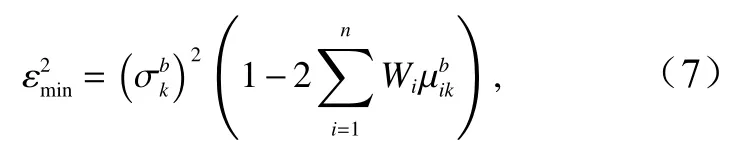
初估场误差协相关利用高斯函数表示

式中，x、y分别表示经向和纬向；i、j表示不同的观测点 ； λx、 λy分 别 表 示 经 向 和 纬 向 相 关 尺 度 ， 当xi等 于xj时，计算纬向上不同距离的相关系数，通过最小二乘法拟合得到 λx和Ax，当yi等于yj时，采用同样的方法可以得到 λy和Ay；A表示分析格点与邻域的最大相关系数，这里取Ax和Ay的均值。本文将OSTIA海表温度分析产品插值到2 km网格上作为初始的初估场，然后再以上一时次的海表温度融合产品加上当前时次海表温度增量作为初估场。以分析格点的位置为中心，利用半径500 km以内初估场数据计算A、 λx和 λy。图7为2017年4月初估场误差协相关的 λx、 λy和A。

由图7a和图7b可知，近岸海域初估场误差的经向和纬向相关尺度明显小于远海，这是由于近岸海域存在许多入海河口且受人类活动影响较大，水环境复杂，海表温度随时间变化较快且在空间上分布不均匀，造成近岸海域初估场误差的相关尺度较小；经向相关尺度大于相应的纬向相关尺度，这是由于海表温度随纬度变化较大而在经向变化较小。由图7c可知，参数A反映了分析格点与其邻域的最大相关系数，平均值为0.88，表明分析格点与其邻域具有较高的相关性。

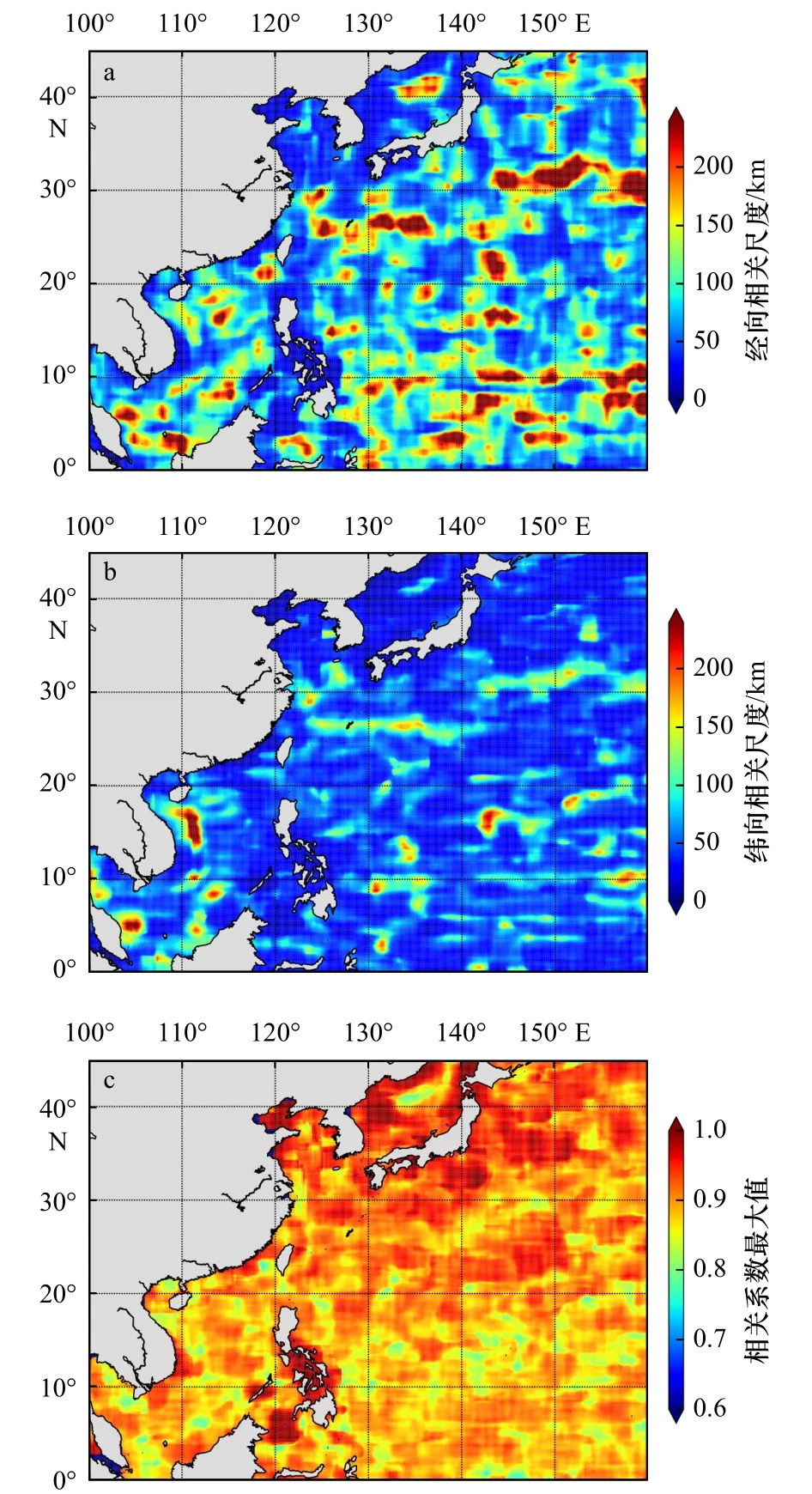
图7 2017年4月初估场误差协相关的 λ x （a）、 λ y（b）和 A（c）Fig.7 The λx(a), λy (b), and A (c) of the estimated initial field in April 2017

图8为经日变化订正、偏差订正后的海表温度观测数据和最优插值海表温度融合产品，时间为2017年4月3日18:00。由于云、降雨等因素的影响，图8a存在大量的缺失数据，经最优插值融合后，图8b海表温度融合产品实现了空间上的全覆盖。对比图8a和图8b可以发现，最优插值海表温度融合产品保留了海表温度观测数据的细节特征。

4 实验验证

为了检验逐时次海表温度融合处理方法的效果和精度，本文选择西北太平洋海域的Himawari-8 AHI海表温度、GCOM-W1 AMSR2海表温度和NERA-GOOS现场观测资料进行融合实验。针对实验结果，从融合结果个例分析和精度检验两个方面评价逐时次海表温度融合产品。

4.1 融合结果个例分析

本文选取吕宋海峡及其周边海域进行个例分析，经纬度范围为 15°～28°N，112°～127°E，时间为 2017年8月17日，图9为00:00和14:00的海表温度融合结果及日增温情况，图10为14:00的多平台交叉校准（CCMP）海面风速空间分布情况。由图9a和图9b可知，融合后的海表温度覆盖了整个海域，反映了海表温度的空间分布情况。海表温度在台湾海峡西岸存在明显的低值区，然后沿西北–东南走向，逐渐升高。由图9c可知，A和B区存在明显的日增温现象，而C和D区的日增温较小，这与太阳辐射和海面风速有关，如图3和图4。8月份太阳辐射较强，有利于日增温，下面主要分析海面风速与图9c日增温空间分布的相关性。在图10中，A和B区的风速偏低，有利于日增温；C和D区风速较大，有利于表层海水混合，日增温不明显，这与图9c日增温的空间分布特征基本一致，间接证实海表温度融合处理结果的准确性。

图8 经日变化订正、偏差订正后的海表温度观测数据（a）和最优插值海表温度融合产品（b）Fig.8 The observed sea surface temperature using the diurnal variation and bias corrections(a), and the fused sea surface temperature using the optimal interpolation(b)

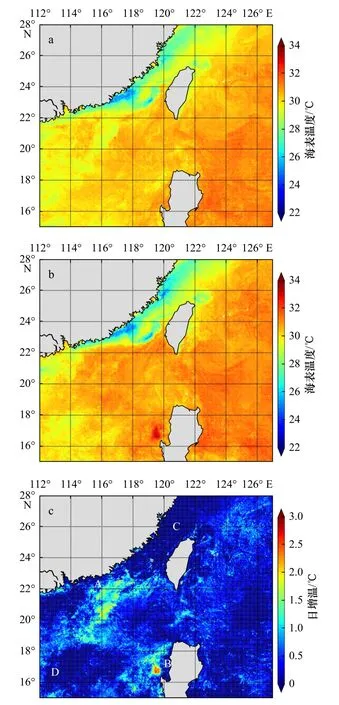
图9 2017年8月17日 00:00时（a）和 14:00时（b）的海表温度融合结果及日增温情况（c）Fig.9 The daily warming of sea surface temperature (c) and the fusion products of sea surface temperature at 00:00 (a) and 14:00 (b) on August 17, 2017

4.2 精度检验

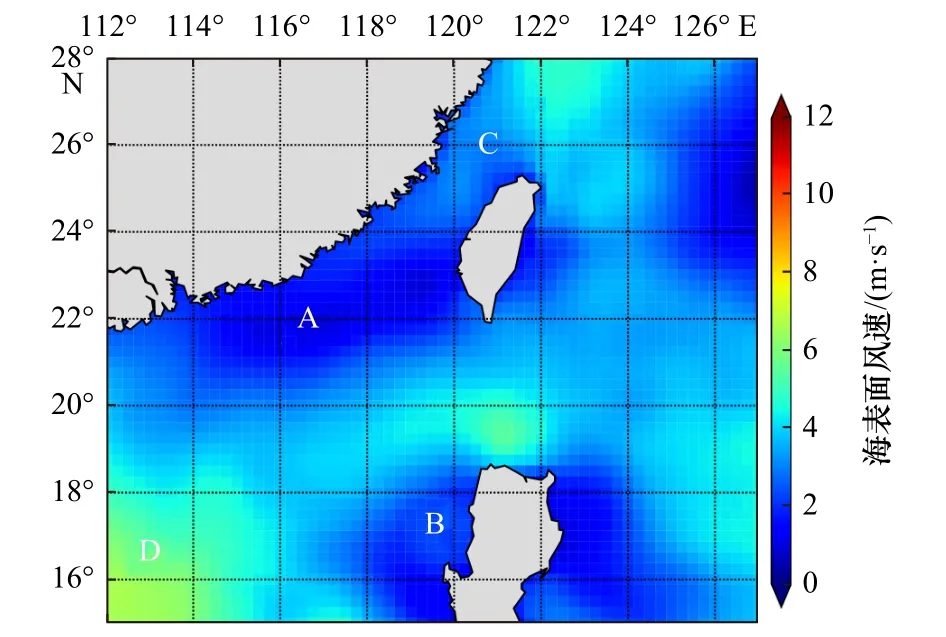
图10 2017年8月17日14:00时的CCMP海面风速Fig.10 The CCMP sea surface wind speed at 14:00 on August 17, 2017

本文选择2017年1月、4月、7月和10月的NERAGOOS现场观测资料对海表温度融合结果进行精度检验，二者在空间上的匹配标准是观测位置间隔小于2 km、时间上的匹配标准是观测时间间隔小于30 min，匹配数据点为16 418个，随机选取2 000个现场观测数据参与海表温度融合，剩余14 418个现场观测数据用于海表温度融合结果精度检验，检验结果如图11所示。图11a为NERA-GOOS现场观测资料和海表温度融合结果的散点图，数据主要集中在5～30℃之间的对角线附近，NERA-GOOS现场观测资料和海表温度融合结果的均方根误差为0.89℃；图11b为NERA-GOOS现场观测资料与海表温度融合结果偏差的直方图，海表温度融合结果略小于NERAGOOS现场观测资料，偏差的平均值为0.09℃、中值为0.12℃、最大值为3.04℃、最小值为–3.34℃，这说明本文的海表温度融合产品具有较高的精度。

5 结论

Himawari-8 AHI海表温度具有高频次、高空间分辨率的特点，但受云雾影响大，空间覆盖度较低。GCOM-W1 AMSR2海表温度空间覆盖度较高，但空间分辨率低，且在近岸精度不高。本文以Himawari-8 AHI海表温度为基础，融合GCOM-W1 AMSR2海表温度和NERA-GOOS现场观测资料，生成高空间分辨率、高精度、全覆盖的西北太平洋逐时次海表温度融合产品。

为了充分利用邻近时刻海表温度，本文利用Himawari-8 AHI海表温度和ECWMF海面风速研究分析了海表温度随时间、风速、太阳辐射的变化情况，建立了Himawari-8 AHI海表温度日变化模型，实现邻近时刻海表温度的订正；为了消除多源海表温度间系统偏差，本文以Himawari-8 AHI海表温度为目标数据，利用泊松方程改变GCOM-W1 AMSR2海表温度的梯度场，使其与Himawari-8 AHI海表温度梯度场的差异最小化，实现多源海表温度间偏差订正；由于最优插值实现上的简单性、计算代价的合理性，本文选用最优插值实现订正后的Himawari-8 AHI海表温度、GCOM-W1 AMSR2海表温度以及NERA-GOOS现场观测资料的融合。为了验证逐时次海表温度融合产品的效果和精度，本文选取吕宋海峡及其周边海域进行个例分析，发现海表温度日增温情况与海面风速具有较好的相关性，间接证实了海表温度融合结果的准确性；然后，利用NERA-GOOS现场观测资料与海表温度融合产品进行对比分析，二者均方根误差为0.89 ℃,其中，海表温度融合产品的值略偏低，偏差为0.09 ℃,说明本文的海表温度融合产品与现场观测海表温度具有较好的一致性。

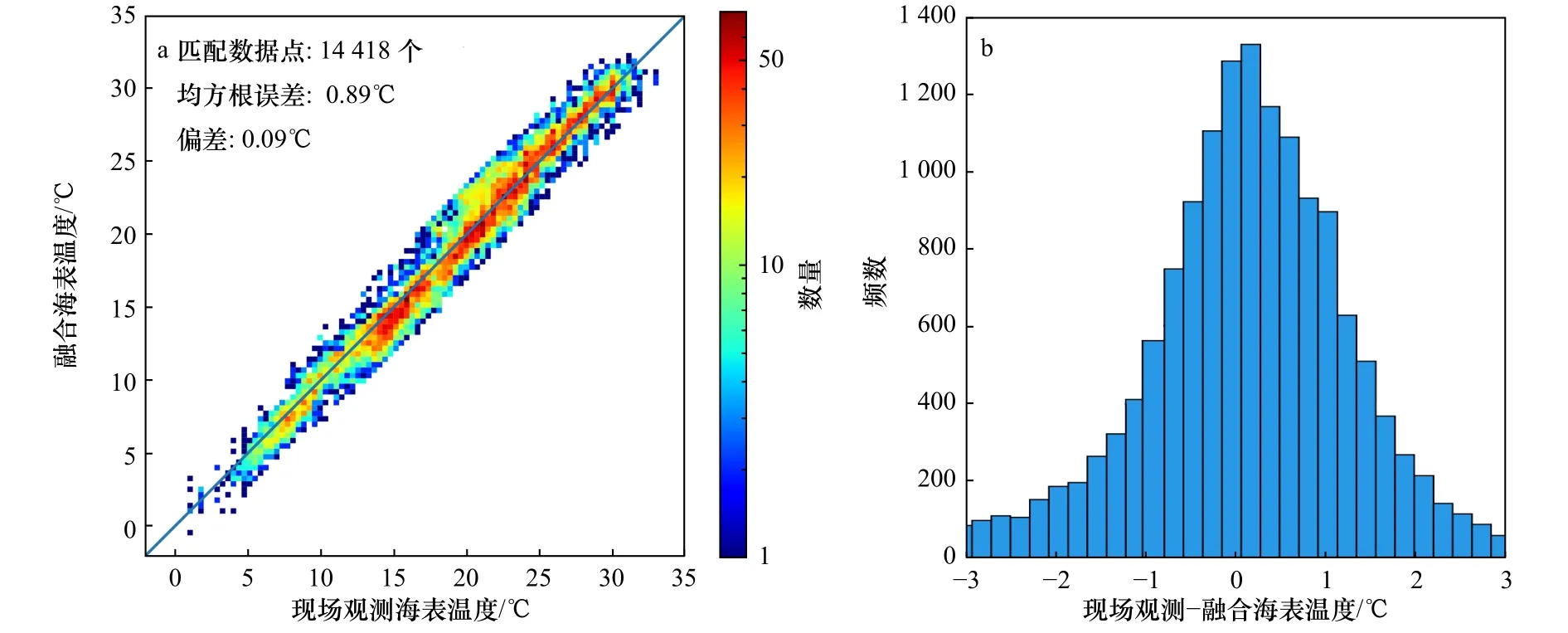
图11 海表温度融合结果精度检验Fig.11 The validation of sea surface temperature fusion products

逐时次的海表温度融合产品对于研究海气相互作用、海洋热动力过程和气候变化具有重要意义，同时也为水声设备应用提供重要的数据支撑。利用逐时次的海表温度融合产品计算海表温度的日增温，可定性分析海表温度对声呐的探测效果影响，也可结合水声传播模型和三维温盐数据定量计算声呐作用距离。

随着FY-4A、HY-1C和HY-2B等国产卫星海表温度产品投入业务化应用，逐时次海表温度融合可利用的国产卫星数据源逐步增多，下一步将利用国产卫星数据源建立海表温度日变化模型，发展多源海表温度间系统偏差方法，研发逐时次的国产化海表温度融合产品，满足水声设备应用的保障需求以及海气相互作用、海洋热动力过程和气候变化的研究需求。

致谢：感谢日本宇宙航空研究开发机构提供的Himawari-8 AHI海表温度产品（https://www.eorc.jaxa.jp/ptree/），欧洲中期天气预报中心提供的海表风速产品（http://apps.ecmwf.int/datasets/data/interim-fulldaily/），日本海洋数据中心提供的NEAR-GOOS现场观测资料（http://near-goos1.jodc.go.jp/index.html）。